基于FS模型的设计施工总承包联合体领导-成员风险分配策略分析
2016-04-11陈永泰盛昭瀚
丁 翔, 陈永泰, 盛昭瀚, 李 迁
(1. 南京大学政府管理学院,江苏 南京 210093; 2.南京审计大学工程管理学院,江苏 南京 211815;3.南京大学工程管理学院,江苏 南京 210093)
基于FS模型的设计施工总承包联合体领导-成员风险分配策略分析
丁 翔1, 陈永泰2,3, 盛昭瀚3, 李 迁3
(1. 南京大学政府管理学院,江苏 南京 210093; 2.南京审计大学工程管理学院,江苏 南京 211815;3.南京大学工程管理学院,江苏 南京 210093)
合理的风险分配是实施设计施工总承包模式的重要保障。在分析联合体成员公平偏好的基础上,通过对FS模型的改进,构建了联合体牵头方与联合体成员之间的Stackelberg博弈模型,从联合体成员嫉妒负效用以及同情正效用两方面,对联合体牵头方的最优风险分配以及联合体成员的最优风险投入进行了均衡分析。最后,采用调研获取的参数分析了不同风险承担比例下联合体成员的公平偏好系数对联合体成员风险投入、联合体成员效用、联合体牵头方效用以及联合体整体绩效的影响。特别地,联合体成员应对不同风险分配方案时会产生不同心理偏好,低分配比例情景下嫉妒偏好的增强会提高自身效用但降低联合体牵头方的效用;高分配比例情景下嫉妒偏好的增强不仅会降低联合体成员效用还会降低联合体牵头方以及整体效用,相反,同情偏好对联合体绩效具有正向调节作用。
设计施工总承包; 联合体; Stackelburg博弈; FS模型; 风险分配
1 引言
大型工程普遍存在成本超支、延期完工的情况,主要原因之一在于工程建设主体对风险的认知不足且风险管理的责任界面不清[1-2]。不合理的风险分配不仅会导致工程成本的增加[3],还会引发承包商的抵触行为,包括在投标合同中额外增加高额的风险准备金或者在工程建设过程中降低工程质量等[4-5]。因此,厘清风险承担主体及其风险承担比例是有效开展工程风险管理的首要任务[4]。
设计施工总承包(Design-Build或者Design-Construct)是国内外大型工程常用的一种项目管理模式,业主将工程的勘察、设计、采购、施工等建设任务交由一个主体承包,该主体对工程的质量、进度、成本等工程目标全面负责[6]。由于我国招标投标法对承包商有资质认定,使得承担设计施工总承包项目的投标人通常是由多个企业组成的联合体。相比传统的设计-招标-施工(DBB模式),采用单一合同的DB模式能够有效地为项目业主减少合同与协调界面,原本由业主处理的多代理人之间的争议与冲突改由联合体解决[6],并且项目业主通过总承包合同在相当大程度上将设计、施工等多个环节的风险转移给联合体[7]。因此,在设计施工总承包模式下,联合体是工程风险的主要承担者。
由于我国招标投标法对规定设计施工总承包联合体需由若干个相互独立的法人机构组成,不同主体所追求的利益和目标又不尽相同,导致联合体内部各主体的风险界面存在复杂性与模糊性,鉴于此,为提高项目绩效和实现工程建设目标,构建合理的联合体风险分配机制成为设计施工总承包模式实施的重点与难点。
学术界关于项目风险分配的研究可追溯到上世纪八十年代,当时的研究主要从合同激励的视角分析项目风险分担与工程成本之间的关系[8-9]。之后的学者分别运用定性和定量等多种方法对风险分配问题开展了研究。Yeo和Tiong[10]、Yamaguchi等[11]、Jin Xiaohua[12]和Doloi[12]分别采用了案例分析和实证调研等方法构建了风险分配矩阵,并定性分析了基于合同的风险分配机制[10-12]。Lam等[5]、Xu Yelin等[13]、Khazaeni等[14]运用模糊推理的相关方法构建风险分配的指标体系,并重点分析了各级指标对风险分配绩效的权重[4-5,13]。Jin Xiaohua和Zhang Guomin[14]采用ANN(人工神经网络)对PPP项目的风险指标进行了分析,并构建指标体系对工程参建主体的风险承担责任进行评价[14]。早期研究主要围绕风险分配的影响因素开展。近年来,关于风险分配的研究开始定量的分析风险分配模型。Medda[15]采用博弈方法建立了风险分配谈判的将讨价还价模型。Nasirzadeh[16]引入Zadeh扩展原理建立了风险分配模型,并指出不同风险分配比例下工程成本的动态变化趋势。Chang Chenyu[17]将委托代理理论引入项目风险管理中,在考虑参与方风险偏好的基础上,通过数理分析给出了风险分配比例与合同激励效果的关系。
总体来说,现有研究极大的丰富了风险分配的理论和方法,这些研究主要集中在风险分配过程的影响要素分析,或者风险分配与合同激励的关系研究,缺乏对主导方风险分配策略以及参与方风险应对策略的深入研究。此外,现有研究没有考虑到工程建设主体的行为认知,相关定量研究都是建立在“理性经济人”假设的基础上。然而,行为经济学的研究指出行为人在关注个人最大收益的同时,还会关注分配是否公平[18-19],大量的实验(信任博弈、独裁者博弈和礼物交换博弈等)成功验证了人的公平偏好是普遍、客观存在的,会对人的行为产生影响[20-22]。主体在公平认知行为倾向作用下,对自己感到不公平的事情以己方利益受损为代价采取行动达到惩罚对方的目的[23-25]。此外,Mohamed等[26]、Bowen[27]通过实证研究也指出承包商具有合谋、投机取巧等非完全理性行为。因此,考虑到联合体成员的非理性行为,本文将参与方的公平感知引入风险分配模型中。
目前有关行为主体公平感知的理论模型主要有两类,一类是重视收益结果的公平,最具代表性的是FS(Fair Process and Social Preferences)模型[28]和ERC(Equity, Reciprocity and Competition)模型[29],这两种模型都主张人不是纯粹自利的,在关注自己收益的同时还具有不平等厌恶心理[30]。另一类是强调主体的心理博弈,主要为Rabin Fairness模型[31],该模型需要构建大量人的心理行为,没有给出具体的数理模型。由于ERC模型需要参考多主体间的平均收益,而本文研究的联合体成员之间是异质性主体,且联合体牵头方与不同联合体成员之间的风险界定也不同,故不存在平均的风险分配比例。因此,本文将借鉴参考对象为他人且模型简洁的FS模型[30]。
在上述研究的基础上,本文将公平偏好理论拓展到项目风险管理领域,结合工程风险分配的特殊性,对FS模型进行改进,构建设计施工总承包项目中联合体内部的风险分配模型,重点分析公平偏好对联合体牵头方风险分配决策、联合体成员风险投入应对策略的影响。在此基础上,采用数值分析的方法分析了不同风险承担比例下联合体成员的公平偏好系数对联合体成员风险投入、联合体成员效用、联合体牵头方效用以及联合体整体绩效的影响。
2 建模思路与基本假设
在设计施工总承包模式下,联合体通常由一个牵头单位和N个负责设计、施工、咨询等建设任务的成员(N≥2)组成,联合体牵头单位会分别与不同成员的风险承担比例进行协商。联合体作为一个整体与项目业主签订DB总承包合同,但是在联合体内部,成员之间则没有特定的契约关系,成员之间的合作是在联合体牵头单位的统筹管理下并以“联合体协议”为指引进行的,因此,联合体成员的之间的关系是建立在“收益共享、风险共担”的基础上[32]。在没有契约约束的情况下,如何实现联合体内部公平的“风险共担”对于联合体牵头单位来说存在极大的困难,原因在于,参与工程建设的联合体成员都是独立法人,或者说是相互独立的企业/机构,从经济学角度来说,联合体成员作为独立法人是以追求自身效用最大化为目标,因此,联合体牵头方对联合体成员提出的风险分配比例和成员所愿意投入的风险管理成本之间属于一种典型的Stackelberg博弈:基于风险规避的考虑,联合体牵头方希望将更多的风险转移,由联合体成员承担,通常来说,风险承担的越多就意味着防范风险的投入就越多,过多的投入会导致收益减少,因此,联合体成员在风险分配比例与风险投入中寻找平衡点并综合考虑自身收益。
与企业管理研究中的虚拟联盟类似,联合体内部的信息资源共享,双方对信息的获得程度基本一致[33],在工程实践中,联合体牵头方的信息可能占优,但并非绝对优势,因此本文研究的是完备信息下联合体牵头方与联合体成员之间的博弈。
本文考虑由一个牵头方(L)与n个成员(Mi)组成的联合体。依据设计施工总承包合同,联合体成员承担不同的任务,联合体成员执行不同的任务时需应对不同的风险,因此,联合体牵头方与不同成员需要协调不同类型的风险。例如,国内某在建的大型桥梁工程采用了设计施工总承包模式,其总承包联合体由多家单位组成,其中联合体总牵头人为施工方,联合体成员分别承担人工岛设计、隧道设计、设计咨询、施工质量管理等不同任务,在工程实施过程中联合体牵头方需要针对不同任务与联合体成员划分责任界面,确定风险承担比例,联合体成员依据风险承担比例确定风险投入。在此基础上,本文提出以下研究假设:
假设1:联合体牵头方依据自身效用函数确定最优的风险分配比例,联合体成员依据自身效用函数确定最优的风险投入,效用函数受其公平偏好的影响。联合体成员判断风险分配是否公平的标准在于对比双方在风险防范中所得的收益。
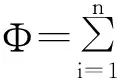
假设3:根据联合体成员承担任务的不同,联合体牵头方分别与联合体成员确定相应的风险分配比例。由于风险类型的差异性,联合体成员的风险投入决策不存在依赖性,即Mi的风险投入只受到L提出的风险分配比例以及自身公平偏好的影响。
假设4:当联合体风险防范时,联合体使用风险包干基金支付所有费用(包括联合体事故发生前的风险投入),此费用视为联合体的损失。
在以上假设前提下,本文主要通过讨论联合体牵头方和联合体成员在风险分配过程中的期望效用,在考虑主体公平感知的情景下,分析联合体牵头方风险分配策略以及联合体成员风险应对策略,从而构建联合体风险分配的最优化模型,如图1所示。

图1 设计施工总承包联合体风险分配研究框架
着重研究完备信息下公平偏好对联合体成员风险投入的影响,公平偏好对联合体牵头方效用的影响,以及公平偏好对联合体整体效用的影响。
3 模型建立与分析
3.1 联合体成员效用分析

(1)
随着承包商投入风险防范的费用c提高,其风险控制水平随之加强[35],因此,联合体成员Mi的风险控制水平可表示为公式(2):
(2)
其中,cmax为理想状态下的风险投入费用,表示风险控制达到最高水平时所需的风险投入费用,由工程属性、行业技术水平等因素决定,在一定时间内属于外生给定常量。
以往的实证研究表明工程风险防范效果(RiskManagementPerformance)与承包商的风险控制能力(RiskManagementCapability)有关[36]。具体来说,风险被控制的可能性随着风险控制能力的提升而提高[37],因此,本文假设了一种工程风险控制概率的计算公式:
P(qi,ci)=αi′r(ci)+ε
(3a)
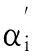
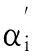
P(qi,ci)=αici+ε
(3b)


在上述分析的基础上,并考虑到联合体成员是风险中性的,本文设定,当联合体牵头方L提出风险承担比例qi,联合体成员Mi投入成本ci用于风险管理时,联合体成员Mi的期望收益如公式(4)所示:
(4)
3.2 联合体牵头方效用分析
联合体牵头方L收益同样来源于风险包干基金,当联合体成员Mi成功控制工程风险时,按照风险分配比例联合体牵头方L从中获益。例如,当联合体成员Mi在一个施工阶段严格按照工程进度且没有发生工程超支情况完成任务时,延期或停工风险以及成本超支风险在一个施工周期内没有发生,因此,联合体牵头方L依据风险激励机制从风险包干基金中收益。当Mi风险控制成功时联合体牵头方的收益可表示为公式(5):
(5)



(6)
3.3 改进的FS模型
理论界关于公平感知的研究认为,当主体收益低于其他主体收益时,会对该主体的效用带来损失,因此一般在效用函数中引入利润差异等形式来刻画主体的公平关切心理[23]。
本文以主体之间的收益差距为参照描述主体的公平偏好行为,借鉴FS模型的思想,对主体的公平偏好行为进行建模[38]。当联合体牵头方提出风险承担比例后,联合体成员会测算自身的期望收益,并与联合体牵头方的期望收益做比较。
当联合体成员Mi期望收益低于联合体牵头方的收益时,即UMi(qi,ci)
(7)
其中,δMi、γMi分别代表联合体成员Mi的两种心理偏好系数,即嫉妒心理系数和自满心理系数。心理偏好系数越大,表示联合体成员越重视自身效用的公平。
在实际的DB项目中,联合体牵头人往往要付出更多的成本用于风险防范,因为联合体牵头人承担了主要的工程建设任务,负责协调并安排联合体所有成员的工作和任务,并且联合体牵头人通常在总承包合同中占有了最大的份额、承载了最多的利益,因此,对于联合体牵头人来说,尽最大可能降低工程风险、确保工程的按时按质是其核心任务与目标,因此,联合体牵头方不存在对于风险收益的公平感知,始终保持为:
(8)
4 模型求解
4.1 嫉妒偏好影响下的博弈求解

结合公式(4)、(6)、(7)可得,在嫉妒偏好影响下联合体成员Mi的期望效用变为:
(9)
由此可得联合体成员风险投入的最优化决策模型:

(10)
(11)
(12)

(13)
此亦为联合体牵头方效用最优化的参与约束条件。
然后,运用逆推归纳法[40]求出联合体牵头方的最优风险分配比例。由于联合体牵头方与联合体成员为完全信息博弈,所以联合体牵头方同样知道联合体成员的最优决策[41],由此联合体牵头方将选择最优风险分配比例,结合公式(6)和(13),联合体牵头方的效用最优化决策模型:
(14)
由于联合体牵头方与成员分别签订风险分配协议,且不同成员的风险类型不同,彼此的风险投入决策不存在依赖性,因此计算联合体牵头方的最优总收益可转化为计算联合体牵头方在每种风险上获取的风险收益最优化。即联合体牵头方的最优化风险分配模型可转化为:
(15)

(16)
(17)
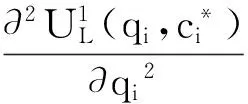
(18)
4.2 同情偏好影响下的博弈求解

结合公式(4)、(6)、(7)可得,在同情偏好影响下联合体成员Mi的期望效用变为:
(19)

(20)
同样运用逆推归纳法[40]求出联合体牵头方的最优风险分配比例。结合公式(6)和(20),联合体牵头方的效用最优化决策模型:
(21)

(22)
4.3 博弈结论分析
4.3.1 公平偏好对联合体成员风险投入决策的影响
将δMi=0代入公式(13)中,得到无嫉妒偏好的联合体成员最优风险投入,c*(0)=qiΦi,则:
(23)
由于qi<1,Φi>0,δMi≥0,从而有ci* 此外,对公式(13)求关于δMi的一阶偏导,得到: (24) 结论1 在嫉妒偏好的影响下,联合体成员的最优风险投入低于没有公平偏好的成员。随着联合体成员嫉妒心理系数的增大,联合体成员的最优风险投入费用将越来越低。 将γMi=0代入公式(20)中,得到无同情偏好的联合体成员最优风险投入ci**(0)=qiΦi,则: (25) 由于qi<1,Φi>0,0<γMi<1,从而有ci**>ci**(0)。 此外,对公式(20)求关于γMi的一阶偏导,得到: (26) 结论2 在同情偏好的影响下,联合体成员的最优风险投入高于没有风险偏好的成员。随着联合体成员同情心理系数的增大,联合体成员的最优风险投入费用将越来越高。 4.3.2 公平偏好对联合体牵头方风险分配决策的影响 (27) 同时,对公式(17) 求关于δM的一阶偏导,得到: (28) 结论3联合体牵头方分配给有嫉妒偏好的联合体成员的风险承担比例高于没有公平偏好的成员。随着联合体成员嫉妒心理系数的增大,联合体牵头方需要让联合体成员承担更高的风险分担比例以保障自身效用。 (29) 同时,对公式(17) 求关于γMi的一阶偏导,得到: (30) 结论4 联合体牵头方制定的风险分配方案受到联合体成员同情偏好的影响,联合体牵头方提出由具有同情偏好的成员承担的风险比例随着该成员同情心理系数的增大而减小。并且,在与同情心理系数在0到0.5之间的联合体成员合作时,联合体牵头方提出的最优风险分配比例要低于无公平偏好的成员。当联合体成员同情心理系数高于0.5时,联合体牵头方的最优风险分配比例高于与无公平偏好的成员合作时的比例。 通过构建博弈模型,本文从公平偏好的视角分析了牵头方的风险分配策略以及联合体成员的风险投入对策。需要指出的是,由于博弈模型求出的联合体成员最优风险投入以及联合体牵头方的最优风险分配的结果过于复杂,为了使联合体风险分配模型更具有实践指导性,本文通过对国内某在建的设计施工总承包联合体的调研,获得了与本模型相关的基本参数,并借助计算机对模型进行数值分析,以便明晰公平偏好对联合体风险分配策略的影响机理。 针对联合体可能存在的设计风险,本文在与工程现场工作人员的访谈中获取了联合体牵头方A与承担设计任务的联合体成员B之间的基本参数,Φ=500000,α′=2.6,cmax=480000。借鉴于FS模型的假设[28,42],δm>γm,令δm∈[0,1],γm∈[0,1)。 由于在工程实践中联合体牵头方对于联合体成员的公平偏好信息(包括嫉妒心理系数以及同情心理系数)难以获取,因此,本文基于联合体牵头方的视角,分析三种情景下(风险分配比例分别为q=0.4、q=0.6和q=0.8)公平偏好系数对于各主体绩效以及联合体整体绩效的影响。如图2、3所示。 图2 嫉妒偏好对联合体系统绩效的影响 图3 同情偏好对联合体系统绩效的影响 当q=0.6时,联合体成员受到同情正效用的影响,见图3。不难发现,同情偏好对于联合体系统绩效同样有着重要影响。联合体成员的风险投入随着其对公平感知的加强而提高,当联合体成员的同情心理系数达到0.47时,联合体成员的风险投入达到业内最高投入水平。从过程上看,公平偏好越强烈越有利于联合体整体实现效用最大化。由此可见,同情偏好的存在对于联合体系统绩效具有正向调节作用,当联合体牵头方的风险分配策略激发联合体成员的同情偏好时,联合体牵头方和联合体成员的效用能达到较高水平从而实现双赢。 由此可得到如下管理启示:(1)作为“非理性经济人”, 联合体成员在关注自身效益最大化的同时,更加注重与其他主体的收益差距,无论是提高还是降低自身的投入,都是为了拉近不同主体间的收益差距,并且,当联合体成员对公平的偏好越强烈时,其做出的回应就越剧烈。(2)风险分配策略对联合体系统绩效的提升具有决定性影响。不同的风险分配策略会引发联合体成员不同的风险应对行为,进而产生不同的风险控制效果。(3)设计合理的风险分配策略,关键在于识别并系统把握联合体成员的公平偏好特征。对待不同类型的联合体成员,联合体牵头方需要采用不同的风险分配策略,从而有效调动联合体成员投入更多人力、物力、财力以及相关资源应对风险。 本文通过构建联合体牵头方和联合体成员之间的博弈模型以及算例分析,从公平偏好的视角对联合体牵头方的风险分配策略以及联合体成员的风险应对策略进行分析。主要结论表明:公平偏好对于联合体系统效用具有重要影响,联合体成员的嫉妒偏好会导致系统绩效降低,相反,同情偏好对系统绩效具有正向调节作用;风险分配策略对系统效用最大化具有决定性影响;联合体牵头方只有在有效识别成员公平偏好特征后才能制定合理的风险分配策略,从而调动并促进联合体其他成员加强风险管理工作。 本文构建了基于FS模型的风险分配机制,旨在弥补传统风险管理中缺乏主体行为研究的不足之处,并且希望借助数理模型构建对于联合体具有实际指导意义的风险分配机制。然而,构建合理的联合体风险分配机制是涉及多层次、多方位的复杂系统工程,对于联合体各成员的行为刻画更需要借鉴于经济学、行为科学、组织科学等多学科的交叉融合,因此,本文只是在该领域的初步尝试,后续研究需要在跨学科理念指导下,构建更符合现实系统的风险分配模型,对其进行更为精细的研究。 [1] Flyvbjerg B. Over budget, over time, over and over again: Managing major projects[M]// Morris PWG, Pinto J K, Soderlund J. The Oxford handbook of project management.Oxford: Oxford University Press, 2011: 321-344. [2] Flyvbjerg B. What you should know about megaprojects and why: An overview[J]. Project Management Journal, 2014, 45(2): 6-19. [3] Hartman F, Snelgrove P, Ashrafi R. Effective wording to improve risk allocation in lump sum contracts[J]. Journal of Construction Engineering and Management, 1997, 123(4):379-387. [4] Khazaeni G, Khanzadi M,Afshar A. Optimum risk allocation model for construction contracts: Fuzzy TOPSIS approach[J]. Canadian Journal of Civil Engineering, 2012, 39(7):789- 800. [5] Lam K C, Wang Dan, Patricia T K, et al. Modelling risk allocation decision in construction contracts[J]. International Journal of Project Management, 2007, 25 (5):485-493. [6] Levi S. Design-build project delivery[M]. Windsor: McGraw Hill Financial Inc., 2007. [7] The Construction Management Association of America. An owner’s guide to project delivery methods[R]. 2012 https://cmaanet.org/files/. [8] Barnes M. How to allocate risks in construction contracts[J]. International Journal of Project Management, 1983, 1(1): 24-28. [9] Abu-Hijleh S F. and Ibbs C W. Schedule-based construction incentives[J]. Journal of Construction and Engineering Management, 1989, 115(3):430-443. [10] Yeo K T, Tiong R L K.Positive management of differences for risk reduction in BOT projects[J]. International Journal of Project Management, 2000, 18(4): 257-265. [11] Yamaguchi H, Uher T E, Runeson G. Risk allocation in PFI projects[C]//Proceedings of the 17th Association of Researchers in Construction Management (ARCOM) Annual Conference. Salford, UK, 2001,Septem ber 5-7. [12] Jin Xiaohua H,Doloi H. Interpreting risk allocation mechanism in public-private partnership projects: an empirical study in a transaction cost economics perspective[J].Construction Management and Economics, 2008, 26(7):707-721. [13] Xu Yelin, Chan A P C, Yeung J F Y. Developing a fuzzy risk allocation model for PPP projects in China[J]. Journal of Construction Engineering and Management, 2010, 136 (8):894-903. [14] Jin Xiaohua, Zhang Guomin. Modelling optimal risk allocation in PPP projects using artificial neural networks[J]. International Journal of Project Management, 2011, 29 (5):591-603. [15] Medda F. A game theory approach for the allocation of risks in transport public private partnerships[J]. International Journal of Project Management, 2007, 25 (3):213-218. [16] Nasirzadeh F, Khanzadi M, Rezaie M. Dynamic modeling of the quantitative risk allocation in construction projects[J]. International Journal of Project Management, 2014, 32 (3):442-451. [17] Chang Chenyu.Principal-agent model of risk allocation in construction contracts and its critique[J]. Journal of Construction Engineering and Management, 2014, 140 (1): 04013032-1-9. [18] Camerer C F, Lowensten G, Rabin M. Advances in behavioral economics[M].Princeton: Princeton University Press, 2004. [19] Camerer C F. Behavioral game theory: Experiments in strategic interaction[M]. Princeton:Princeton University Press, 2003. [20] Henrich J, Boyd R, Bowles S, et al. In search of homo economicus: Behavioral experiments in 15 small-scale societies[J]. American Economic Review, 2001, 91(2): 73-78. [21] Clark A E, Masclet D, Villeval M. Effort and comparison income: Experimental and survey evidence[J]. Industrial and Labor Relations Review, 2010, 63(3): 407-426. [22] Kube S, Marechal M A, Puppe C. The currency of reciprocity: Gift exchange in the workplace[J]. American Economic Review, 2012, 102(4):1644-1662. [23] Ho T H, Zhang Juanjuan. Designing pricing contracts for boundedly rational customers: Does the framing of the fixed fee matter[J]? Management Science,2008, 54(4): 686-700. [24] Loch C H, Wu Yaozhong. Social preferences and supply chain performance:an experimental study[J]. Management Science, 2008, 54(11):1835-1849. [25] Katok E, Pavlov V. Fairness in supply chain contracts:A laboratory study[J]. Journal of Operations Management, 2013, 31(3):129-137. [26] Mohamed K A, Khoury S S, Hafez S M. Contractor’s decision for bid profit reduction within opportunistic bidding behavior of claims recovery[J]. International Journal of Project Management, 2011, 29(1):93-107. [27] Bowen P A, Edwards P J, Catell K.Corruption in the South African construction industry: A thematic analysis of verbatim comments from survey participants[J]. Construction Management and Economics, 2012, 30(10):885-901. [28] Fehr E, Schmidt K M. A theory of fairness, competition and cooperation[J]. Quarterly Journal of Economics, 1999, 114(3): 817-868. [29] Bolton G E, Ockenfels A.A theory of equity, reciprocity and competition[J]. American Economic Review, 2000, 90(1):166-193. [30] 晏艳阳,金鹏. 公平偏好下的多任务目标与国企高管薪酬激励[J].中国管理科学,2014,22(7):82-93. [31] Rabin M. Incorporating fairness into game theory and economics[J]. American Economic Review, 1993, 83(5):1281-1302. [32] 盛昭瀚,张劲文,李迁,等.基于计算实验的工程供应链研究[M].上海:上海三联书店出版社,2013. [33] Johansson P, Johansson C.Perceptions and challenges with knowledge sharing-enterprise collaboration in a virtual aeronautical enterprise[C]//Proceedings of the 18thinternational conference on engineering design: Impacting society through engineering design, Copenhagen, Denmark,2011, August 15-19. [34] Laffont J J, Martimort D. The theory of incentives:the principal-agent model[M]. Princeton:Princeton University Press, 2001. [35] Chapman C, Ward S. Project risk management: processes, techniques, and insights[M]. New York:John Wiley & Sons, 2003. [36] Zou P X W, Chen Ying, Chan T Y. Understanding and improving your risk management capability: Assessment model for construction organizations[J]. Journal of Construction Engineering and Management, 2010, 136(8): 854-863. [37] Xiong Bo, Skitmore M, Xia Bo, et al. Examining the influence of participant performance factors on contractor satisfaction: A structural equation model[J]. International Journal of Project Management, 2014, 32(3):482-491. [38] 李真,孟庆峰,盛昭瀚,等.工程质量优化的承包商群体激励效率演化分析[J].中国管理科学,2012,20(3):112-121. [39] Camerer C F, Loewenstein G. Psychological perspectives on justice: Theory and applications[M]. Cambridge:Cambridge University Press, 1993. [40] Shaked A, Sutton J. Involuntary unemployment as a perfect equilibrium in a bargaining model[J]. Econometrica, 1984, 52(6):1351-1364. [41] Neumann V J, Oscar M. Theory of games and economic behavior[M].Princeton: Princeton University Press, 2004. [42] Fehr E, Schmidt K M. Fairness, incentives, and contractual choices[J]. European economic review, 2000, 44(4-6):1057-1068. Optimal Leader-follower Risk Allocation Strategies for Design-Build Coalitions Based on Fair Process and Social Preferences (FS) Model DING Xiang1, CHEN Yong-tai2,3, SHENG Zhao-han3, LI Qian3 (1.School of Government, Nanjing University, Nanjing 210093,China;2. School of Management and Engineering,Nanjing Audit University Nanjing 211815,China;3.School of Management and Engineering, Nanjing University, Nanjing 210093,China) Design-build is proved to be a preferred project delivery method for infrastructure projects, yet how to design an appropriate and fair risk sharing mechanism within design-build coalition (DBC) is essential to achieve project success. Further, despite the well documented literature on risk allocation for infrastructure projects, prior research has largely neglected participants’ social preference which is proved to be salience in affecting their attitudes, behavior and, in turn, decision-making process. Accordingly, participants’ risk management behavior will be situational, which means they will response to the risk sharing mechanism based on their perception whether the allocation ratio is fair to them. To address the gaps, a quantitative approach is presented to analyze risk sharing arrangement in design-build project by considering DBC member's fairness preference. Fehr and Schmidt's inequity aversion (IA) model is integrated into the proposed risk allocation model. The objective of this paper is to derive results for DBC leader's optimal risk-sharing ratio and DBC members' optimal risk-management effort simultaneously. The derivation is based on solving a restrained optimization problem using the conception and methods from Stackelberg game theory. Analysis results show that: (1) DBC members are prone to different fairness preference (in terms of envy preference and sympathy preference) depending on the value of risk-sharing ratio; (2) DBC members’ optimal risk investment decreases with the enhancement of IA level when DBC member is envy preference; (3) DBC members’ optimal risk investment increases with the enhancement of IA level when DBC members are sympathy preference; (4) It is beneficial for DBC leader to allocate more risk-sharing ratio to DBC members as their levels of envious preference increase; (5) DBC leader can allocate less risk-sharing ratio to DBC members as their levels of sympathy preference increase.Practically, the article will benefit for those who write DBC negotiation with recommendations on risk allocation strategies. Theoretically, this research sheds a light on establishing optimal risk allocation via considering members’ social preference, and fills the gaps where traditional risk allocation models are based on the hypothesis of completely rational person. Accordingly, literature is enriched by providing mathematical evidence on designing a fair risk allocation strategy and, in turn, future research directions are provided for scholars to explore empirical evidence to support notions proposed in this paper. design-build; coalition; stakelberg game theory; FS model; risk allocation 1003-207(2016)07-0043-11 10.16381/j.cnki.issn1003-207x.2016.07.006 2014-12-09; 2015-05-08 国家自然科学基金资助项目(71300521,71301070,71301062,71471077,71571098); 教育部人文社会科学研究青年基金项目(12YJCZH020);交通运输部建设科技项目(2013318282310) 陈永泰(1977-),男(汉族),甘肃会宁人,南京审计大学工程管理学院,副教授,研究方向:项目管理,E-mail:emailschen@163.com. C930 A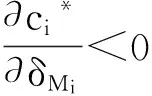
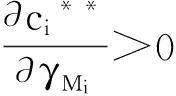





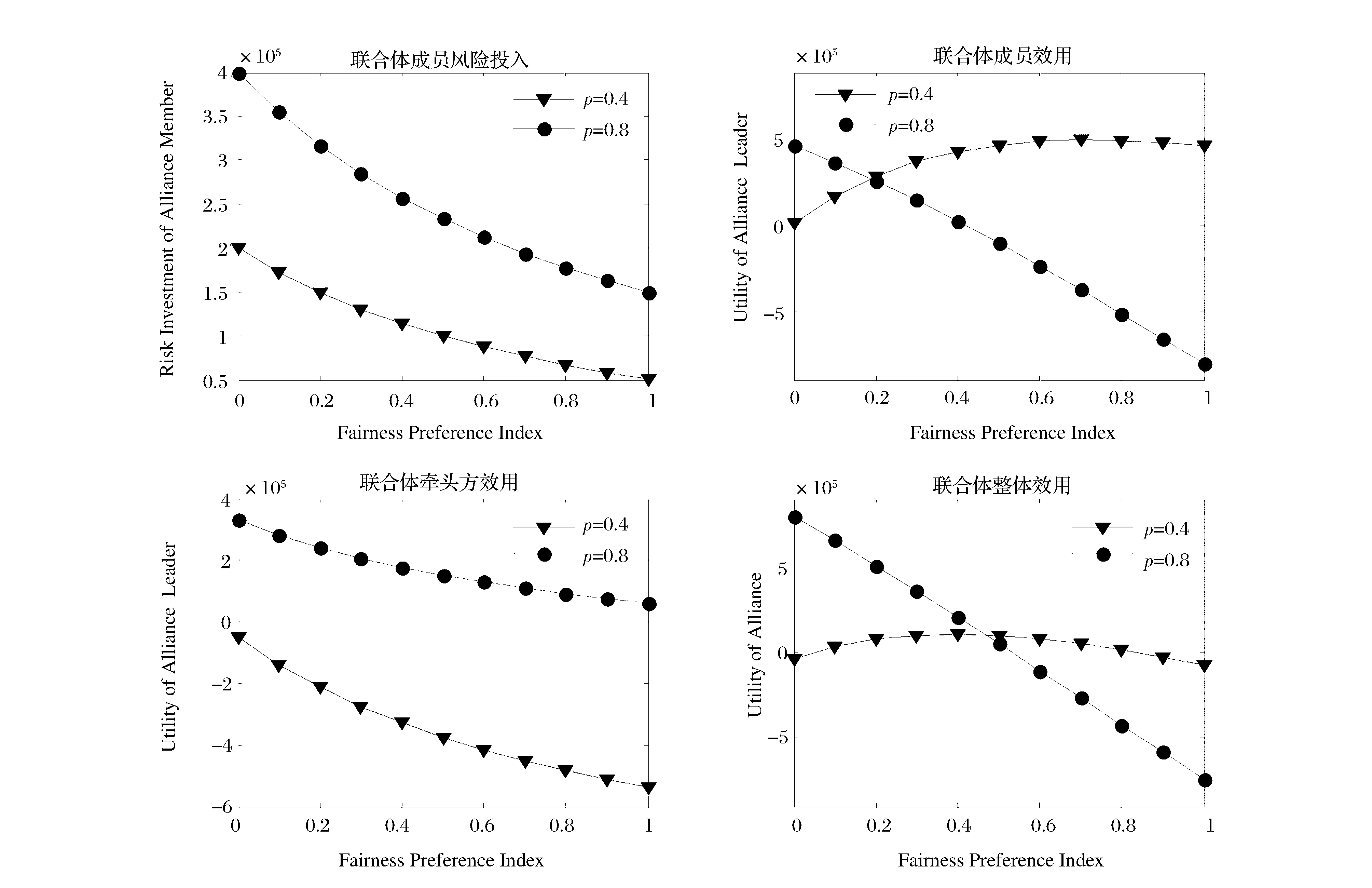
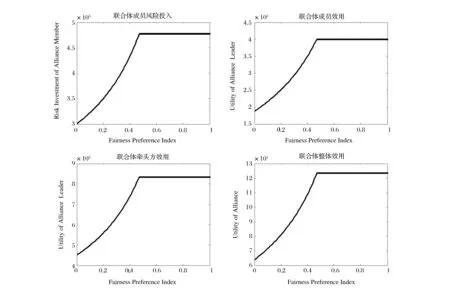
5 算例分析
6 结语
