基于或有可转换证券的投资和融资决策
2016-04-11赵志明杨招军
赵志明,杨招军,王 淼
(1. 湘潭大学商学院,湖南 湘潭 410005; 2.南方科技大学金融系,广东 深圳 518055;3.湖南大学金融与统计学院,湖南 长沙 410079)
基于或有可转换证券的投资和融资决策
赵志明1,杨招军2,王 淼3
(1. 湘潭大学商学院,湖南 湘潭 410005; 2.南方科技大学金融系,广东 深圳 518055;3.湖南大学金融与统计学院,湖南 长沙 410079)
通过引入新的融资工具或有可转换证券(CCS),应用最优控制和最优停时理论、分析基于实物期权视角下的公司最优投融资决策问题,计算了公司各证券价值、有限期破产概率及公司最优资本结构,获得代理成本为零的一个充分条件。数值仿真及静态比较分析表明:CCS作为融资工具能够降低投资项目破产风险和普通债券的收益率差价,能够显著增加实物期权的价值,促使管理者提前投资,且显著降低代理成本。
或有资本;实物期权;资本结构;最优停时
1 引言
2008年全球金融危机致使各国政府对系统性重要银行(Systematically Important Banks)采取了规模空前的救助行动。由于这一外部救助(Bail out)存在很大的道德风险,因此,如何提高银行自我救助(Bail In)能力是摆在各国政府及学者面前的共同挑战。解决这一问题的秘密武器—或有可转换债券(Contingent Convertible Bonds,以下简称CCB或CC)应运而生。英国劳埃德银行集团和荷兰合作银行分别于2009 年和2010 年率先发行CCB。CCB是一种混合证券,兼具股权和债权的特点。在发行初期阶段,CCB表现为债券特性,投资者获得固定券息,且公司能获得相应的税收减免;一旦公司陷入经营困境或是外部经济环境极度恶化,CCB自动转换为公司股权,以帮助公司走出困境。
Flannery[1]首先提出CCB这一概念,不过这篇文献仅在定性层面对CCB进行了分析,而Albul等[2]首次建立了严格的定量模型,解析地给出了CCB 的若干性质,分别从发行公司和监管部门的角度考虑了最优资本结构问题。随后许多经济学者对这一新的金融工具进行深入研究。CCB的设计主要涉及转换机制,其包含两个方面:转换方式和转换触发点。在转换方式方面,Metzler和Reesor[3]设定CCB为一次性转换,研究了公司证券的定价和风险问题。Glasserman和Nouri[4]则考虑连续转换方式,一旦公司资本率低于最低监管资本比要求,CCB自动转换为股权以满足资本比要求,直至所有CCB转换完为止。在转换触发点设计方面,Pennacchi[5]以公司市场资本比为触发指标,假设银行资产的收益服从一个跳扩散过程,研究了银行风险参数、合约条款、与CCB 及股权均衡价格的相互关系。McDonald[6]提出双触发机制:以公司股票市场价格和金融景气指数为触发指标,研究了这种触发机制下CCB 的优势和不足。Bolton 和 Samama[7]设计CCB的转换触发是一个美式期权,股东决定转换时刻,并研究了股东、CCB投资者、监管部门之间的相互影响。 Sundaresan和Wang Zhenyu[8]提出不能以公司股票价格作为转换触发点,并指出这种转换机制将导致CCB 的价格出现多重均衡及均衡不存在问题,给出了均衡价格存在的充要条件。
上述关于CCB的文献均考虑转换是单方向的(即只允许CCB由债权转换为股权)。直观上,如果CCB可以在债权和股权之间来回转换,则公司可在不增加其破产风险的条件下获得更多税收减免。基于此,本文引入或有可转换证券(Contingent Convertible Security,以下简称CCS)。CCS首先由Yang Zhaojun 和Zhao Zhiming[9]提出,该文主要考虑资产收益过程为连续情形下的CCS设计及相关性质问题,Yang Zhaojun和Zhao Zhiming[10]则进一步推广到跳扩散情形,但二者都没有考虑基于 CCS 的实物投资问题。CCS类似于CCB,但有本质区别,其主要特征为:依赖于与公司经济健康状况密切相关的两个指标,如公司现金流水平,CCS在债券和股权之间可以自动来回转换。
与本文研究内容密切相关的另一领域为不确定环境下的投资理论。在公司金融中,由于市场环境的日新月异,不确定性已成为影响公司投融资决策的重要因素。实物期权法为管理者在不确定性环境下的投融资决策提供了有利工具。实物期权概念首先由Myers[11]提出。近30多年,许多学者在这一领域进行积极探索。McDonald[12]建立了标准的实物期权模型并研究公司管理者投资、融资决策问题。Dixit和Pindyck[13]系统阐述了实物期权概念。在项目投资中,股东与债权人的利益目标并不完全一致,分析他们之间代理冲突问题是实物期权领域的一个热门方向,Childs[14],Mauer[15]和Andrikopoulos[16]在这方面做出了突出贡献。国内学者在实物期权应用方面也进行了深入研究[17]。如宋小保[18]在实物期权视角下研究股权集中、股东异质对公司投融资决策的影响。
本文贡献在于:一,首次将CCS引入到基于实物期权视角的公司投融资决策领域,发展基于CCS的公司动态投融资决策理论。二,本文发现通过设置合理的CCS转换率可以使股东-债权人代理成本为零,且获得了转换率的解析表达式。现有研究公司动态投融资的文献都没能完全解决股东—债权人代理冲突问题。虽然Lyandres等[19]提出普通可转债可以消除这一代理冲突问题,但仅仅给出了数值解。三,投资项目的价值最大化和破产风险最小化始终是项目管理者关注的核心问题。本文发现基于CCS融资工具的投资者最优投资时机要早于基于CCB或传统资本结构的投资时机,论述了CCS在提高投资项目价值和降低破产概率等方面比普通债券及CCB具有明显优势。本文进一步得到了以公司价值最大化和以股东价值最大化两种目标下的公司最优投资时机和最优资本结构。
本文其余内容安排如下:第二部分为模型建立,计算公司证券及实物期权价值,并且得到股东-债权人代理成本为零的CCS转换率解析式;第三部分为数值分析及比较静态分析;第四部分为结束语。
2 模型建立和公司证券定价
2.1 模型建立
考虑一家公司,拥有一个不可逆、可延迟且收益不确定的风险投资项目,项目投资额(沉没成本)为I。根据实物期权理论,公司的这种投资选择是一个实物期权问题。与普通实物期权不同,本文考虑的沉没成本除通过股东自有资金筹集外,余下部分全部通过发行 CCS和普通债券的融资聚道筹集。代表股东利益的管理层面临两个决策问题:选择最优投资时刻及确定最优资本结构。一旦公司管理者执行实物期权,则通过以下三个金融工具融资:一是普通债券(Straight Bond,以下简称SB),发行量为Ks,其券息为Cs;二是CCS,发行量为Kc,其券息为Cc;余下全部由现有股东出资筹集。代表股东利益的管理层的目的是极大化现有股东的利益。
假定投资项目运行后所产生的税后现金流满足几何布朗运动:
dδt/δt=μdt+σdZt,δ0给定
(1)
其中μ,σ为常数,分别为现金流的平均增长率和波动率,dt为时间增量,Z为定义在完备概率空间(Ω,F,Q)上的标准布朗运动,测度Q为风险中性概率测度。事实上,假定项目预期现金流服从几何布朗运动是比较常见的做法,如McDonald等[12]、Dixit等[13]、Childs等[14]。这一假定能比较准确地刻画项目的现金流过程,同时,在数学处理上也比较方便,因此,在研究实物期权问题时对项目现金流进行这样假设得到广泛认可。
假设无风险利率为r,税率为r,破产损失率为α。在项目运行良好(即δt>δd)时,CCS表现为债券形式;当项目经营恶化(即δt<δe)时,CCS由债权状态转为股权,转换率为β。参照Kozid等[20],我们设定δe≡φ1(Cs+Cc),δd≡φ2(Cs+Cc),其中0<φ1<φ2由监管机构确定。不失一般性,假定管理者在项目预期现金流处于较高水平时选择执行项目。自然地,在投资初始时点T0,我们假定CCS为债权状态。
接下来,分析CCS投资者的收益构成。定义停时T1≡inf{t>T0|δt≤δe},由上面分析知,当t∈[T0,T1),CCS为债权状态,一旦现金流δt首次等于或低于δe,也即当t>T1时,CCS转换为公司股权;设破产边界为δb,再定义破产停时Tb≡inf{t>T0|δt≤δb}和T2≡inf{t>T1,t
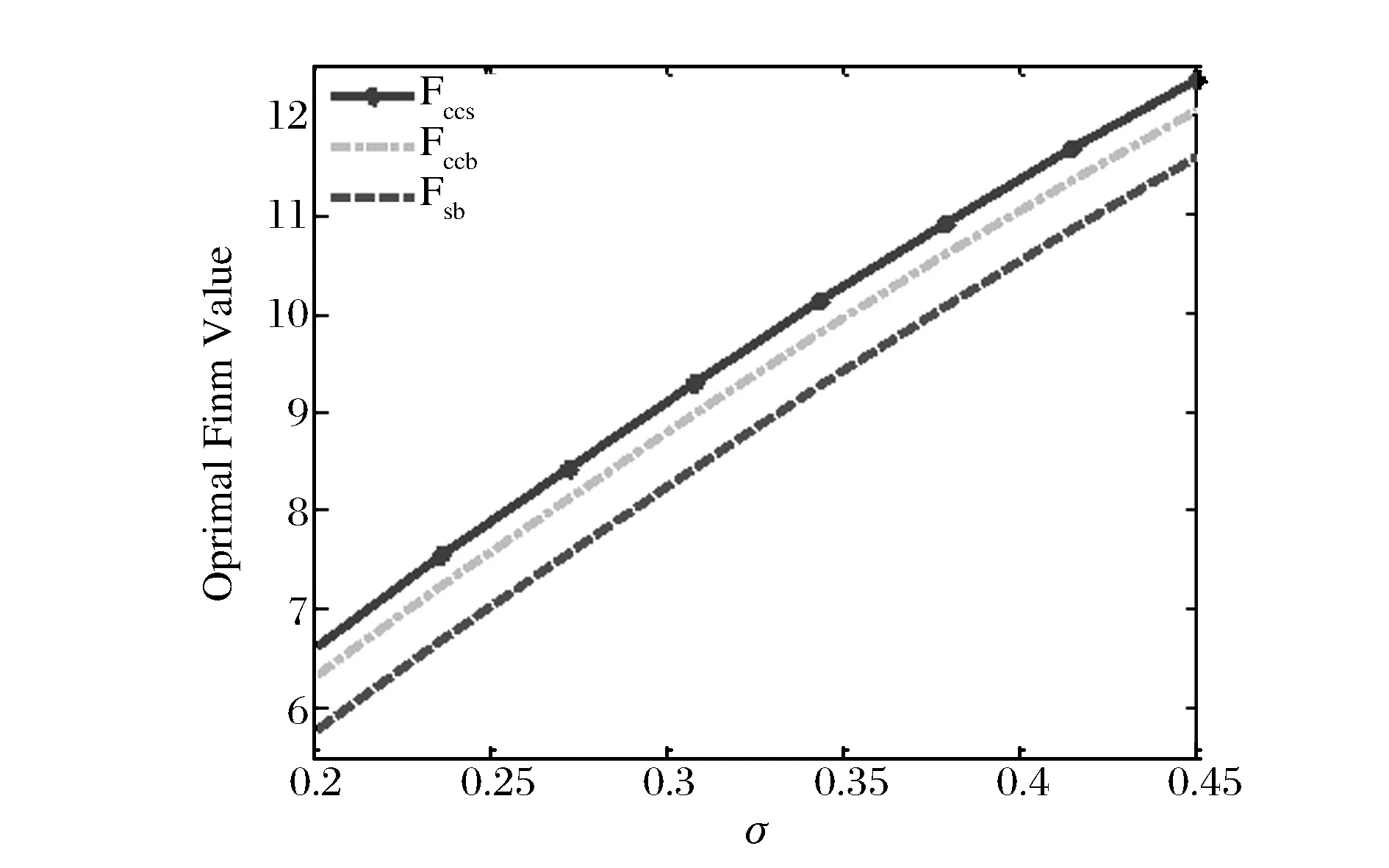
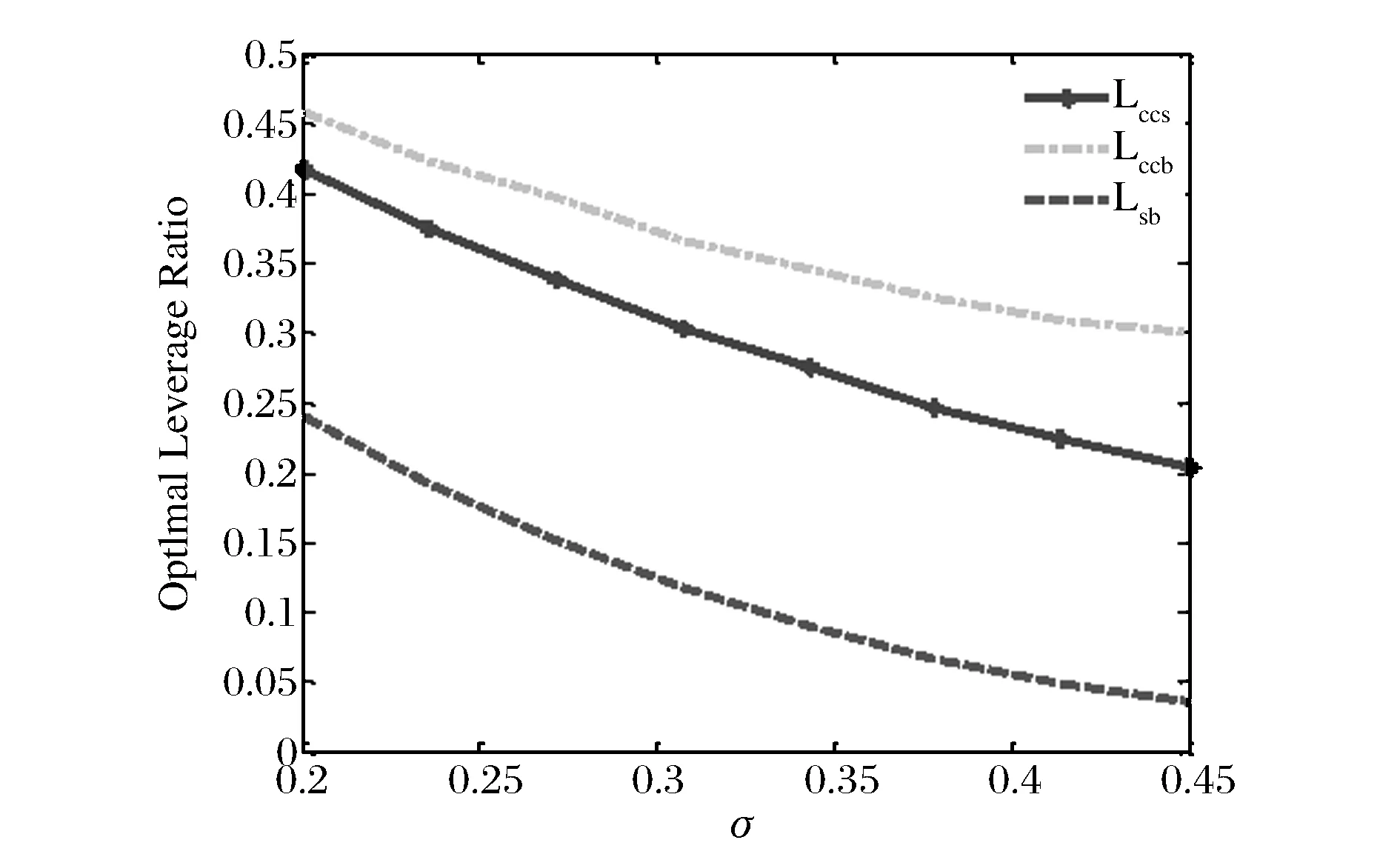
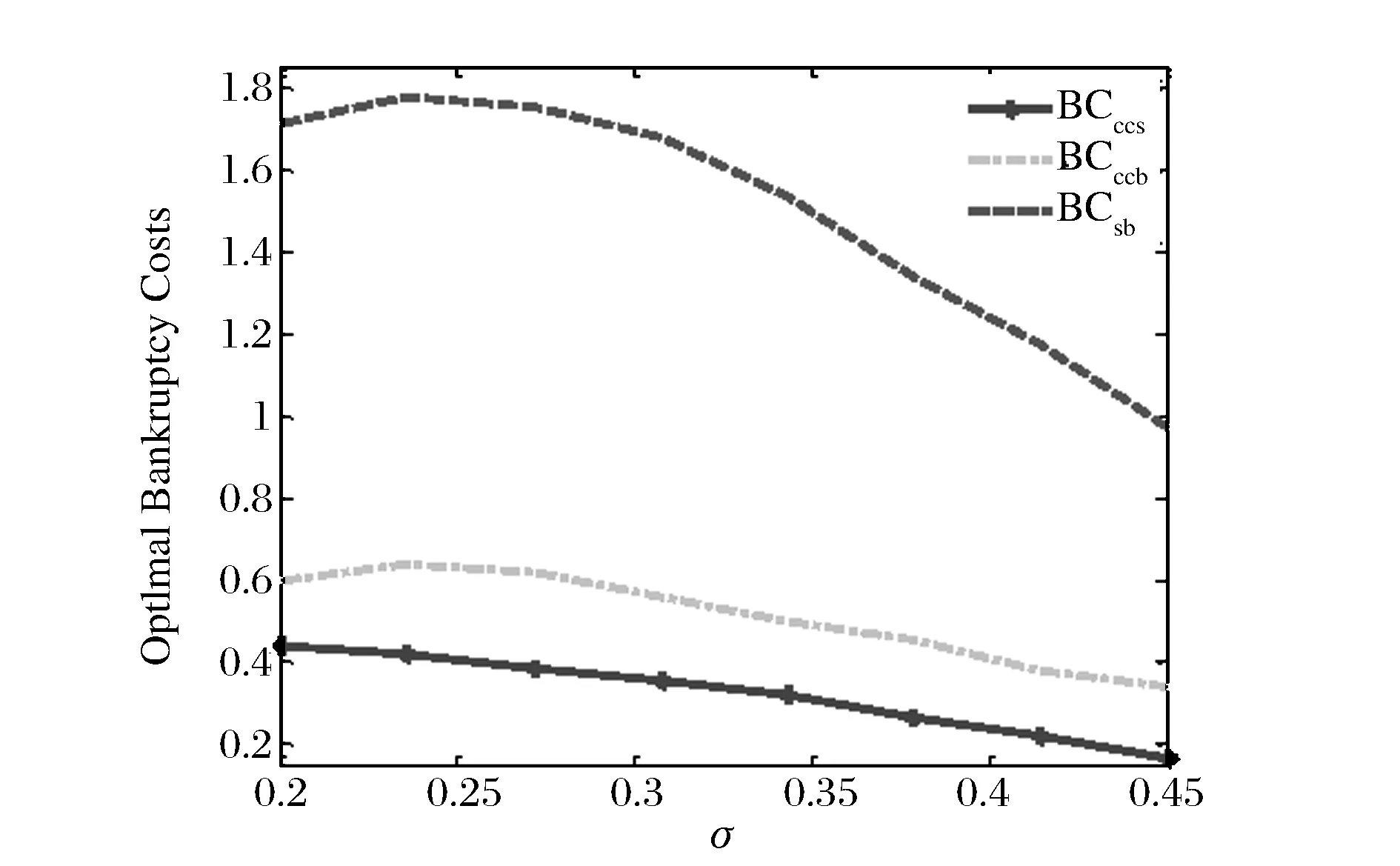
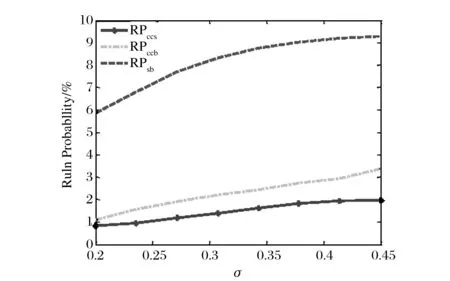
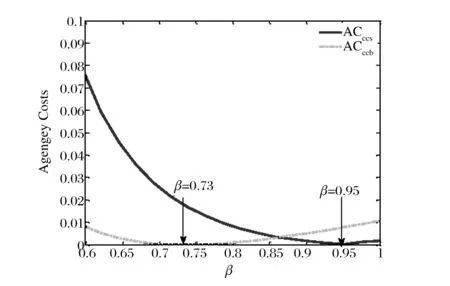
其中k=0,1,2,3…,T2k+1≡inf{t>T2k,t 2.2 公司证券定价 接下来,我们将在风险中性定价原则下计算公司证券的价值。普通债券所有者在公司破产之前一直获得稳定券息Cs。当公司破产时,扣除公司破产成本,债权人获得剩余价值。利用动态规划原理可得,普通债券价值D满足: μxDx+0.5σ2x2Dxx+Cs=rD,x>δb (2) (3) 其中第一个等式经济意义为当现金流趋于无穷大时,CCS表现为无风险债券,其价值为券息与无风险利率比值,即Cs/r;第二个等式表示当公司破产水平时,债权人获得公司剩余价值的1-α。我们通常假定r>μ,在这个条件下,式(3)债券价值D为有限值。利用条件(3)可求得债券价值为: (4) 在公司执行实物期权时刻,CCS为债权状态,投资者获得券息Cs,记此时CCS价值为Vd,并记股权状态下CCS价值为Ve。 定理1:在公司宣布破产前,CCS处于债权状态(或股权状态),对应价值分别为Vd(Ve),我们有: (5) 其中系数A2,A3,A4满足下列线性方程组: (6) 证明:为计算或有可转换证券CCS的价值,需分两种情况讨论: 首先,在CCS为债权状态时,CCS持有者获得连续券息Cc,直至其现金流δt≤δe,CCS转换为公司股权,则其价值Vd满足如下微分方程: (7) 边界条件: (8) 其中等一个等式表示经济意义与式(3)第一个等式一致;第二个等式为价值匹配条件:现金流达到转股点δe时,CCS在两种状态下价值相同。显然,式(7)通解为: 系数A2我们下面将给出具体形式。 其次,当CCS转换为股权状态时,CCS持有者成为公司新的股东,与原股东共同分享公司息税后现金流,则CCS投资者得到现金流为β(δt-(1-τ)Cs),因此,股权状态下CCS的价值Ve满足如下微分方程: (9) 边界条件为: Ve(δd)=Vd(δd)和Ve(δb)=0 (10) 其中第一个等式与式(8)第二个等式经济意义一致,即价值匹配条件;第二个等式表示为当公司现金流达到破产水平δb时,CCS投资者获得公司剩余价值为零。式(9)通解为: 其中A3,A4由边界条件确定。利用式(10)并化简后可得系数A2,A3,A4满足矩阵(6),证毕。 原始股权价值与CCS所处债权状态(股权状态)有关,分别记其价值为Ed(Ee)。当CCS处于债权状态时,公司支付券息Cs+Cc,股东获得现金流为δt-(1-τ)(Cs+Cc)(一旦现金流δt-(1-τ)(Cs+Cc)为负时,公司稀释股权,以偿付债息。参见Glasserman[4]及SongDandan和YangZhaojun[21];当CCS为股权状态时,公司支付券息,息税后净利润由CCS投资者和原始股东共同所有,原始股东获得1-β比例,也即(1-β)(δt-(1-τ)Cs)。 定理2:在公司破产之前, 原始股权价值Ed(Ee)满足: (11) 其中系数A5,A6,A7满足下列线性方程组: (12) 证明:定理二证明思路类似于定理一。这里不再累赘,证毕。 在已知公司各证券价值的条件下,利用式(4)、(5)、(11),可得公司总价值TV为: (13) 2.3 实物期权定价及最优投融资策略 在公司执行实物期权之前,项目不产生现金流。记期权价值为,股东选择适当投资时机以使股权价值最大,也即求解以下最优停时问题: (14) (15) (16) 管理者确定最优融资规模也即确定Cs,Cc使得股东价值最大化。因此,我们需求解以下二元最优化问题: (17) 2.4 代理冲突 (18) 类似文献Mauer等[15]和Andrikopoulos[16],我们定义冲突成本为: (19) (20) 这个结果本质上与SongDandan和YangZhaojun(2016)[21]结果一致。 3.1 数值比较 本节我们分析公司引入或有可转换证券(CCS)作为融资工具对实物期权的影响。假设项目可利用三种方式获得投资所需成本:第一种仅以股权和债券(SB)融资,记为方式A;第二种为股权、SB以及CCB,记为方式B;第三种为股权、SB以及CCS记为方式C。参考Pennacchi[5]和Song Dandan等[21],本文模型基本参数设为:现金流平均增长率μ=0.01,无风险利率r=0.05,现金流波动率σ=0.25,破产损失率α=0.5,税率τ=0.35,初始现金流δ0=1,沉没成本I=35,CCS转换率β=0.6,由监管机构确定φ1=0.9,φ2=1.1,投资期限T=10。需要说明的是,均衡解往往依赖于初值的选取。然而,本文讨论的是一个具体的经济学问题,我们从经济学直观上考虑可知本文问题的均衡是唯一的,数值计算也支持这一观点,其结论也是符合经济学意义的。 从图1我们可以看出,CCS对提升期权价值有显著影响。随着项目风险的增加,期权的价值也单调增加。同时可以看出:存在或有资本情况下,投资者所获得的实物期权价值远高于传统资本结构下的期权价值。更重要的是,在引入CCS后,实物期权价值在方式B的基础上,又得到大幅度提高。也就是说,与CCB相比,CCS能显著提高实物期权的价值。如在项目风险σ=0.27时,采用方式A、B、C融资,其项目价值分别为7.55、8.11和8.42;方式B在A的基础上提高7.4%;而方式C可提高11.5%。因此,发行CCS进行项目融资能在很大程度上吸引投资者入场,从而提升市场的参与度。新兴行业与高科技行业由于其创新性以及未来收益的不确定性使得其难以获得初始投资,CCS的引入对其融资具有重要意义。 图1 实物期权价值随风险σ变化规律 图2 最优投资水平随σ变化规律 在有关实物期权的文献中,投资时机的选择是研究者普遍关注的一个问题。从图2可以清楚看出,随着项目风险增加,股东选择最优的投资水平也随之增加。且CC的引入,使得管理者选择最优投资时机比方式A融资结构情形更早,并且在CCS情形下,管理者选择投资时机最早。对此我们的分析是:一,由于或有资本在实物期权实施之后的前期表现为债券,其避税优势使得管理者(本文即股东)愿意更早实施项目;二,或有资本的保险功能也使得管理者愿意早于融资方式A情形承担风险,实施投资项目。 由于CC在公司经营状况陷入困境时,提供公司及时救助的特性,增强了公司抵御风险的能力。而且,CC的债券性质使还得公司能获得税收减免。因此,股东愿意进行更多的债券融资,以减少资金成本。从而,将CC引入公司的资本结构后,管理者必将提高公司杠杆率,从图3我们可以清晰的看到这一特征:在同等风险水平下,包含CCB和CCS的融资方式B和C的最优杠杆率显著高于方式A的杠杆率。同时,我们也注意到:随着风险增加,三种融资结构下公司的最优杠杆率都不断降低。这是因为CCB和CCS虽然能转换为股权,但是并不能完全替代股权。所以随着风险的增加,管理者仍需提高股权比例,降低杠杆率,增强公司的抗风险性。 图3 最优杠杆率随风险σ变化规律 图4 破产成本随风险σ变化规律 图4表明,随着风险增加,公司的破产成本呈下降趋势,其部分原因可以从图3的分析结果中看出。与方式A相比,融资方式B、C极大地降低了破产成本。这是因为,当项目风险增加时,公司管理者选择的最优资本结构会增加或有资本,而减少普通债券,从而也降低了破产边界,减少了破产成本(由表达式可知)。并且,我们看出CCS在减少公司破产成本方面最具优势。公司项目的稳健经营是管理者关注的核心问题之一。在考虑投资期限情形下,我们分析了公司的破产概率变化规律。从图5可以看出,所有资本结构下的公司破产概率都与风险σ呈现正相关性。但是,CCS(CCB)的发行能显著地减少公司破产风险。因此,或有资本,特别是CCS所具有的降低公司风险的特性,将使其受到广泛欢迎。 图5 破产概率随风险σ变化规律 从图6、7我们看到,债券的收益率差价与公司风险呈正相关性。当风险σ增加时,债券的收益率差价也增加。进一步我们发现,公司资本结构中包含CCS(或CCB)时,普通债券SB的收益率差价大幅小于方式A情形,也即公司发行CCS(或CCB)极大降低了普通债券投资者的风险。可见,将CCS、CCB引入资本结构后,将公司总的现金流分割成若干不同的子现金流,一方面显著提升了各个子现金流价值的总和,另一方面可以满足不同风险。 图6 SB收益率差价随风险σ变化规律 图7 CC收益率差价随风险σ变化规律 承受能力和风险结构投资者的投资需求,实现了公司风险在不同融资工具上的分担,比如CCS的引入就极大的降低了普通债券的风险,公司投资者根据自身的风险偏好对公司的不同融资工具进行选择,从而改善投资者的风险承受结构。 图8研究了公司代理成本与转换率β之间的关系。在设定参数Cs=0.4,Cc=1.2条件下,由图8可以看出,代理成本AC呈U型,即随着β增加,代理成本表现出先减后增的趋势。转换率意味对原始股权的稀释,较大β对原始股东是一种惩罚,可避免公司收益越差股东收益越高的无效现象。事实上,如果较小,当δt接近δe,原始股东可以通过“烧钱”促使转换提前实现,从而获利。一般地,股东与债权人的利益并不一致,见刘星[22]。对于CCS情形,在转股率β=0.95条件下,管理者在两种目标下的投资时机是一致的,则代理成本为零。β越大,意味对原始股东惩罚力度越大。为避免惩罚,原始股东会选择延迟投资以降低转换发生可能性。而对于CCB而言,设定β=0.73可满足这一要求。 图8 代理成本随转换率β变化规律 3.2 静态比较分析 本小节研究了波动率等六个重要参数对公司的最优融资结构(Cs,Cc)、最优投资时机δt、实物期权价值F、最优杠杆率L、债券收益率差价(CDs,CDc)及债券代理成本(AC)的影响,且给出了分别以公司价值最大化和股东价值最大化为经营目标的静态比较结果。 首先考虑公司波动率σ变化的影响。随着波动率σ增大,实物期权的价值和投资触发水平正向增加,而代理成本减少。一般情形下,股东愿意提前投资以获得更多税收减免,但当公司面临更大的未来不确定性时,股东有更强动机选择延迟投资,使得股东与债券人的目标趋于一致,从而降低代理成本,此结论与Mauer等[15]一致。例如,波动率σ从0.2增大到0.4,等待投资时机的价值(股权价值最大化情形下)Fe从6.42增加到11.15,投资触发水平则由2.2变为3.86,而代理成本由4.67%变为3.23%。同时,波动率σ增加,意味着公司面临现金流风险增加,公司愿意持有更多CCS而减少SB的持有。相应地,公司最优杠杆率也降低。管理目标的不同对普通债券的收益率差价影响并不大,但显著影响CCS,这点从表1第一栏中容易发现。 接下来我们考虑漂移系数μ,μ为现金流的平均增长率。随着μ增加,表明公司具有更好的未来发展前景,因此实物期权的价值增大,这也鼓励股东选择推迟投资(即更高投资触发水平δl)。同时,我们发现与上面分析情形相反,公司在具有好的发展预期下选择持有更多的普通债券,而减少CCS,原因是显然的。并且债券的收益率差价、代理成本、公司杠杆均与漂移率μ呈反向变化。 表1第三栏分析了无风险利率r改变所产生的影响。r越大则意味更大的折扣率,因此,我们得到了与漂移率相反的结论。如r从0.055增加到0.07,而实物期权价值从5.93减少到2.92,代理成本也由4.20增为4.58。沉没成本I增加导致期权的价值显著减少,相应地,股东推迟投资时机。这与传统的经济理论相一致,高利率和高的沉没成本将在一定程度上抑制投资。但从第四栏我们得到,沉没成本的改变对公司的最优杠杆率几乎没有影响,这一数值结果发现与Childs等[14]和Mauer等[15]一致。下面我们分析税率变化产生的影响。公司最优融资结构均为混合融资,也即包含债权和股权。这是由于债券具有税盾效应,可以提高公司总价值,但同时也提高了公司破产触发水平,这是公司金融基本理论。随着税率τ增加,债券的税盾效应更加明显,则公司将发行更多债券,实物期权价值增加,这从表1第5栏可以清楚看出。同时,股东加速投资(即δl变小)。然而, 债券投资人所面临的风险以及公司代理成本也随税率 呈正向变化。也就是说,随着税率 增加,两种管理目标的不一致性更加明显。 表1 基本参数条件下的静态比较结果 最后,我们分析破产损失率α变化产生的影响。由表1最后一栏的数值可以发现:随着破产损失率α变大,公司减少普通债券的发行,而增加CCS的发行,即用CCS替代部分普通债券。破产损失率α的变大,对投资时机的影响比较微小,但实物期权的价值、债券收益率差价、代理成本均减小。这也表明面临破产损失率的增加,股东的投资目标与公司总目标越接近。 本文考虑基于CCS的公司最优投融资问题,得到了基于融资工具CCS的公司各证券价格显式解,并求得公司的最优资本结构、最优投资触发水平,显式地给出了代理成本为零的一个充分条件。通过数值分析表明:相较于普通公司或发行CCB的公司而言,发行CCS可以进一步显著提高实物期权的价值,降低公司的下行风险、减少公司破产成本;由于CCS的“风险屏蔽”效应,CCS可以显著减少普通债券的风险;CCS显著提升了实物期权的价值进而促使投资者更早地实施投资。总之,在忽略管理成本的条件下,CCS作为一种新型的融资工具,在降低公司破产风险、维护公司稳健经营、减少公司代理成本方面具有显著优势。 [1] Flannery M J. No pain, no gain? Effecting market discipline via reverse convertible debentures[C]//Proceedings of "Rish and Stability in the Financial System" Conference, 2002, June 13-14. [2] Albul B, Jaffee M D, Tchistyi A. Contingent convertible bonds and capital structure decisions[R]. Working Paper, University of Berkeley Coleman Fung Risk Management Research Center, 2010. [3] Metzler A, Reesor R M. Valuation of contingent capital bonds in merton-type structural models[R]. Working Paper, Department of Applied Mathematics, University of Western Ontario, 2011. [4] Glasserman P, Nouri B. Contingent capital with a capital-ratio trigger[J]. Management Science, 2012, 58(10): 1816-1833. [5] Pennacchi G. A structural model of contingent bank capital[R]. Working Paper, University of Illinois at Urbana-Champaign, 2010. [6] McDonald R L. Contingent capital with a dual price trigger[J]. Journal of Financial Stability, 2013, 9(2): 230-241. [7] Bolton P, Samama F. Capital access bonds: contingent capital with an option to convert[J]. Economic Policy, 2012, 27(70): 275-317. [8] Sundaresan S, Wang Zhenyu . On the design of contingent capital with a market trigger[J]. The Journal of Finance, 2015, 70(2): 881-920. [9] Yang Zhaojun, Zhao Zhiming. Contingent capital with repeated interconversion between debt and equity[R]. Available at SSRN 2200883, 2014. [10] Yang Zhaojun, Zhao Zhiming. Valuation and analysis of contingent convertible securities with jump risk[J]. International Review of Financial Analysis, 2015, 41: 124-135. [11] Myers S C. Determinants of corporate borrowing[J]. Journal of Financial Economics, 1977, 5(2): 147-175. [12] McDonald R, Siegel D. The value of waiting to invest[J]. The Quarterly Journal of Economics, 1986, 101(4): 707-727. [13] Dixit A K, Pindyck R S. Investment under uncertainty[M]. Princeton, New Jersey:Princeton University Press, 1994. [14] Childs P D, Mauer D C, Ott S H. Interactions of corporate financing and investment decisions: The effects of agency conflicts[J]. Journal of Financial Economics, 2005, 76(3): 667-690. [15] Mauer D C, Sarkar S. Real option, agency conflicts, and optimal capital structure[J]. Journal of Banking & Finance, 2005, 29(6): 1405-1428. [16] Andrikopoulos A. Irreversible investment, managerial discretion and optimal capital structure[J]. Journal of Banking & Finance, 2009, 33(4): 709-718. [17] 彭程, 杨红, 黄荣. 基于税收利益与破产成本的企业投融资决策互动关系研究[J]. 中国管理科学, 2011, (3): 46-54. [18] 宋小保. 股权集中,投资决策与代理成本[J]. 中国管理科学, 2013, 21(4): 152-161. [19] Lyandres E, Zhdanov A. Convertible debt and investment timing[J]. Journal of Corporate Finance, 2014, 24: 21-37. [20] Koziol C, Lawrenz J. Contingent convertibles. Solving or seeding the next banking crisis?[J]. Journal of Banking & Finance, 2012, 36(1): 90-104. [21] Song Dandan, Yang Zhaojun. Contingent capital, real options and agency costs[J]. International Review of Finance, 2016, 16(1): 3-40. [22] 刘星, 计方, 郝颖. 大股东控制、集团内部资本市场运作与公司现金持有[J]. 中国管理科学, 2014, 22(4): 124-133. Investment and Financing Policy Based on Contingent Convertible Security ZHAO Zhi-ming1, YANG Zhao-jun2, WANG Miao3 (1.Business School, Xiangtan University, Xiangtan 411105, China;2.Department of Finance,South University of Science and Technology of China,Shenzhen 518055,China;3.College of Finance and Statistics,Hunan University,Changsha 410079,China) In this paper, an innovative financing instrument called contingent convertible security (CCS) is introduced. Using the optimal control, optimal stopping and real options theory, the optimal investment and financing decisions of a firm that issues CCS together with equity and the straight bond is examined. The risk-neutral prices of all the corporate securities, ruin probability within a given time horizon and optimal capital structure are provided. It's shown that there is an optimal fraction of equity allocated to the CCS holders upon conversion that eliminates the agency cost of debt. The optimal fraction is given explicitly. The numerical simulation is performed and static comparative analysis is provided. The numerical examples prove the rationality of the model and the validity of conclusions. In particular, It's demostrated the new invented CCS can significantly increase the value of the option to invest. In contrast to the standard capital structure that issues equity and the straight bond only, issuing CCS can lead to as much as 11.5 percent increase in the real option's value but the number declines to 7.4 percent if the contingent convertible bond is issued instead of CCS. CCS decreases bankruptcy risk as well as the yield spread of the straight bond. With a growth of the volatility rate of the investment project, the issuing firm will increase the investment trigger, the amount of CCS issued, instead of the straight bond and the firm’s leverage. contingent capital; real options; capital structure; optimal stopping 1003-207(2016)07-0018-09 10.16381/j.cnki.issn1003-207x.2016.07.003 2014-09-01; 2016-03-28 国家自然科学基金资助项目(71171078,71371068);湘潭大学博士科研启动项目(KZ08069) 杨招军(1964-),男(汉族),湖南人,南方科技大学金融系副教授,博士生导师,研究方向:金融工程、数量金融与风险管理,E-mail:yangzj@sustc.edu.cn. F830 A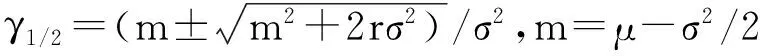








3 数值分析




4 结语
