基于遗传算法的汽车磁流变减振器多目标优化*

郑 玲，牛伯瑶，李以农，庞 剑，李传兵，徐小敏，付江华

(1.重庆大学汽车工程学院，机械传动国家重点实验室，重庆 400044； 2. 汽车噪声振动和安全技术国家重点实验室，重庆 401120； 3.长安汽车工程研究总院，重庆 401120)

2016137

基于遗传算法的汽车磁流变减振器多目标优化*

郑 玲1,2，牛伯瑶1，李以农1，庞 剑2，3，李传兵2，3，徐小敏2，3，付江华2，3

(1.重庆大学汽车工程学院，机械传动国家重点实验室，重庆 400044； 2. 汽车噪声振动和安全技术国家重点实验室，重庆 401120； 3.长安汽车工程研究总院，重庆 401120)

为满足汽车半主动悬架系统的功能需求，宜设计具有大阻尼力调节范围、低能耗、响应迅速的磁流变减振器。本文中分别以磁流变减振器线圈耗能功率和响应时间为目标函数，以输出阻尼力和磁流变减振器阻尼通道处磁感应强度为约束条件，建立了磁流变减振器多目标优化模型，采用带精英策略的非支配排序遗传算法，获得了磁流变减振器多目标优化的最优Pareto解集。结果表明：多目标优化不仅能满足阻尼力可调范围的工程需求，且线圈功率损耗大大减小，响应时间明显缩短，为汽车磁流变减振器的结构优化提供了有效方法。。

磁流变减振器；带精英策略的非支配排序遗传算法；多目标优化

前言

磁流变液体作为一种典型智能材料，一直倍受关注并在诸多工程领域得以应用，例如建筑、汽车、船舶等，具体应用有汽车的减振器[1]、离合器[2]和制动器[3]，桥梁等建筑结构的阻尼器[4]，动力装置隔振器[5]和传感器[6]等。

磁流变减振器由于其响应频率高、阻尼变化范围大、工作电压低、耗能少、调节装置结构简单等特点，在汽车半主动悬架系统中有着广阔的应用前景。美国Lord公司[7]、Delphi公司[8]，德国BASF公司[9]等已经研发出商业产品并在实车中进行试装及性能试验。可见，基于磁流变减振器的汽车半主动悬架系统代表了未来汽车智能悬架系统发展的方向。磁流变减振器作为悬架系统的关键执行元件，其设计直接影响到汽车半主动悬架系统的性能，设计输出阻尼力范围大、响应时间短、能量消耗少的磁流变减振器，对于改善汽车半主动悬架系统性能，加速汽车半主动悬架系统的发展和应用，具有重要的理论意义和工程应用价值。

国内外已有很多学者对磁流变减振器的优化设计方法进行了研究，但大多是将输出阻尼力调节范围、磁流变液工作缝隙处最大磁感应强度或响应时间等设为目标，对磁流变减振器进行结构设计和优化[10-12]。文献[13]中以磁流变阀的调节比例为优化目标，体积为约束条件，对磁流变阀进行了结构优化设计；文献[14]中将输出阻尼力、可调范围和响应常数都列入优化目标，用3个总和为1的系数分别作为其加权系数，本质上仍是单目标优化，对各个子目标的权重很难做到最优配比。文献[15]中以磁流变阀的能量消耗为优化目标，时间响应常数为约束条件，对磁流变阀进行了结构优化，获得了满足调节比例的磁流变阀最优结构尺寸。可见，目前对磁流变器件的结构优化主要是单目标优化，对磁流变器件的结构多目标优化的研究较少。

本文中以轿车磁流变减振器为研究对象，以线圈消耗功率和时间常数为目标函数，以磁流变减振器的输出阻尼力和通道处的磁感应强度为约束条件，研究使目标函数最小化的磁流变减振器多目标结构优化方法。设计变量涉及结构几何参数和线圈参数。采用ANSYS参数化设计语言(APDL)，构建优化设计流程，使电磁场有限元分析纳入结构优化设计全过程，通过对磁流变减振器性能的准确预测，实现其结构设计参数的优化。

1 磁流变减振器结构设计

本文中针对某电动轿车磁流变半主动悬架系统的开发，设计了基于流动模式的单筒单出杆的轿车磁流变减振器，运动时活塞杆进出缸筒会造成压强差，因此在减振器底部设计了气体补偿装置，结构如图1所示。活塞头和减振器缸筒内壁之间构成环形阻尼通道，通过改变线圈中的励磁电流，使环形阻尼通道中的磁感应强度发生变化，从而改变阻尼通道中的磁流变液的黏度，得到连续可调的输出阻尼力。

流动模式工作原理如图2所示。与阻尼通道宽度相比，活塞头外表面和减振器缸筒内表面可视为两固定不动的平行极板，它们之间的缝隙内充满磁流变液，活塞头中绕有线圈，其中的变化电流产生磁场，方向垂直于极板，这时阻尼通道中的磁流变液发生磁流变效应，屈服应力发生变化，实现输出阻尼力连续变化的目的。

流动模式下阻尼通道内磁流变液的流动状态如图3所示。

根据图3，x方向的流量为

(1)

其中：h=R2-R1；h1=r1-R1；h2=R2-r2

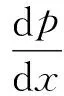
(2)

体积流量为

Q=Apisv=2πRaveq

(3)

结合图2和图3可推导出由外加磁场引起的压力差为

(4)

式中：L为阻尼通道长度；τy为磁场作用下磁流变液的剪切屈服应力；c为减振器设计参数，取值范围从2.07(Δpτ/Δpμ<1)到3.07(Δpτ/Δpμ>100)，经验公式为

(5)

由磁流变液自身黏度引起的压力差为

(6)

(7)

式中：Agap为阻尼通道的环形横截面积；Aave为阻尼通道圆形横截面积。

忽略气体补偿装置的压力，则减振器输出阻尼力F即为

F=Fτ+Fμ=(Δpτ+Δpμ)Apis

(8)

式中：Fτ为剪切阻尼力；Fμ为黏性阻尼力。

因此Fτ和Fμ可写为

(9)

减振器的最大输出阻尼力满足车辆要求是减振器设计的首要标准，同时阻尼力的可调范围越大，表明减振器对不同工况的适应能力越强，因此评价磁流变减振器性能的另一重要指标是磁流变减振器的阻尼比，定义为剪切阻尼力与黏性阻尼力的比值D：

D=Fτ/Fμ

(10)

D值越大，磁流变减振器的输出阻尼力可调范围越大，控制性能越好。

2 优化模型

2.1 优化目标

本文中在所设计磁流变减振器初始尺寸的基础上，对关键部件(活塞头等)的关键尺寸进行优化，以期得到更加合理的结构，使磁流变减振器的性能得以改善。性能优异的磁流变减振器不仅要做到输出阻尼力大、可调范围广，还需反应迅速，因此本文中将响应时间短作为减振器优化目标之一。本文中设计的减振器应用于小型电动车，因此将线圈消耗功率作为另一个优化目标。

首先通过磁路分析推导出磁流变减振器响应时间、线圈消耗功率与结构尺寸的关系。磁流变减振器的磁路结构如图4所示，由活塞头、磁流变液体和减振器缸筒构成闭环回路。

根据磁通量定律和磁路安培法则：

Φ=BkAk

(11)

(12)

式中：Φ为磁通量；Bk和Ak分别为磁路各部分的磁感应强度和磁通面积；N为线圈匝数；I为励磁电流；Hc和lc分别为磁路各部分的磁场强度和磁路长度。

由式(12)可以看出：通过优化活塞头结构，减小活塞头尺寸，能实现在lg不变的情况下，增大阻尼通道处的磁场强度Hg，磁感应强度Bg也随之增大。由磁流变液流变特性，增大阻尼通道处磁感应强度能有效增加磁流变液体的剪切屈服应力，进而增大输出阻尼力，改善磁流变减振器性能。

磁流变减振器中的励磁线圈的消耗功率为

(13)

式中：Rw为励磁线圈电阻；η为能量管理电路的效率。

电阻可表示为

(14)

线圈感应时间即磁路响应时间为

(15)

式中：Lin为励磁线圈的电感；φ为磁路磁通量密度。

2.2 优化变量和约束条件

根据减振器的设计准则和加工工艺要求，可以确定活塞杆直径d、减振器缸筒厚度tw和阻尼通道径向宽度lg取值分别为4，5和1mm。根据图4磁流变减振器磁路结构示意图，各区域磁路长度和线圈平均直径均可由结构参数活塞头半径R1、线圈槽深度tc、阻尼通道长度l和线圈槽长度b表示：

(16)

将上述4个参数定为优化参数，其优化范围如表1所示。

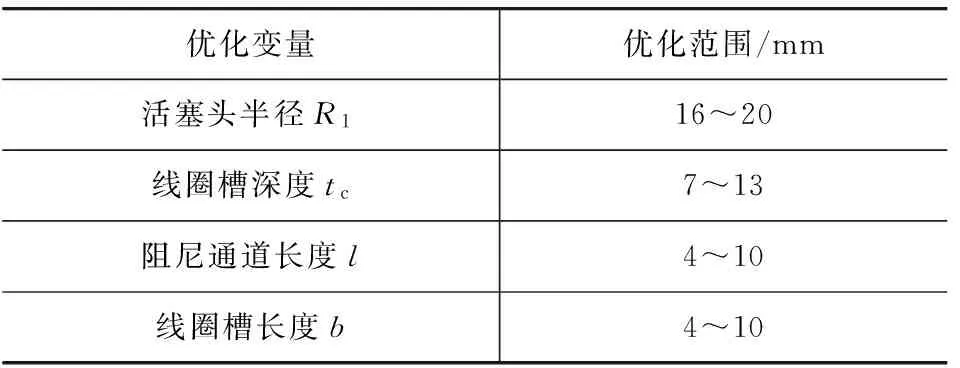
表1 磁流变减振器结构优化变量表

目标函数线圈耗能功率和响应时间可表示为

(17)

(18)

磁流变减振器的约束变量如表2所示。

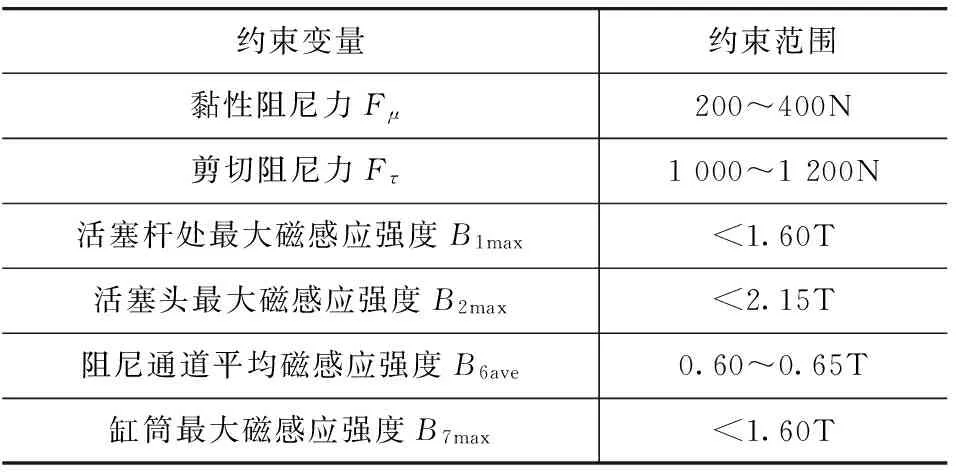
表2 磁流变减振器结构优化约束变量

3 优化方法

本文中优化问题的目标为

(19)

不难看出，磁流变减振器的响应时间和消耗功率作为优化设计的两个子目标函数是相互矛盾的。所以只能在两个子目标函数之间进行折中，使最后的综合结果尽可能达到最优。因此这是一个典型的多目标优化问题，与单目标优化的根本区别在于其优化结果不唯一，而是一组由众多Pareto最优解[17]组成的解集。

传统的多目标优化算法有加权法、约束法、目标规划法和目标满意法等，这些方法计算量小，理论成熟，易于理解和实现。总体而言，传统多目标优化方法的根本思想都是将各子目标聚合成一个带权重系数的单目标函数，然后利用罚函数法将约束最优问题转化为无约束最优化问题，系数由决策者自行确定，或由优化方法自动调整[18]。传统优化方法对目标函数提出了诸多要求，如凸性、连续性或线性，其次权重系数的确定带有很大主观性，且往往不容易获得，因此，传统优化算法的应用受到了很大限制。

目前，越来越多的学者致力于研究更高效的多目标优化算法和理论，如遗传算法、粒子群算法、蚁群算法、模拟退火算法和人工免疫系统等。通过对比分析，本文中选取了遗传算法中的带精英策略的非支配排序遗传算法(NSGA-II)，相比于其他多目标优化算法，NSGA-II的突出特点[19]是鲁棒性好，运行效率高，解集有良好的分布性，特别是对于低维优化问题具有较好的表现，缺点是在高维问题中解集多样性不理想。本文中的多目标优化问题只有2个目标函数，属于低维优化，故不存在上述问题。

NSGA-II[20]的基本思想为：(1)随机生成一定个体数的初始种群，通过非支配排序及遗传算法中的选择、交叉和变异3个基本操作，获得第一代子代种群；(2)从第二代种群开始，将父代种群和子代合并，进行快速非支配排序，同时计算每个非支配层中个体的拥挤度，根据非支配关系和个体的拥挤度，选择合适的个体组成新的父代；(3)重复选择、交叉、变异操作，再次产生新的子代种群；(4)以此为循环，直到进化代数或生成的种群满足程序的终止条件。

本文中磁流变减振器结构优化的基本步骤是：(1)在MATLAB中编写NSGA-II遗传算法主程序，开始运行时随机产生一定规模的初始种群，种群中每一个元素是一组优化变量；(2)将初始种群的每一组变量赋值到APDL语言编写的log文件中，并调用ANSYS进行磁场分析，获得阻尼通道等各处磁感应强度；(3)将数据读出，返回到MATLAB的主程序中，统计计算出阻尼通道磁感应强度平均值，通过代入式(9)、式(17)和式(18)得出阻尼力、线圈消耗功率和响应时间等；(4)通过NSGA-II遗传算法的迭代，获得最优解集。相应的流程如图5所示。

4 优化结果

根据经验将主程序的终止条件设定为迭代次数为100，经过100次迭代后，退出优化程序。输出响应时间和耗能功率2个子目标函数值随迭代次数的变化曲线，如图6和图7所示，可见2个子函数经过迭代最终达到平衡，得到较稳定的函数值。绘制Pareto最优前沿可视图，如图8所示，将其中的第一级个体提出列表，如表3所示，它们互相不可支配，即优化得到的13组最优解，分别代表13组结构参数。

从表3中任选一组数据，如第8组数据：R1=0.0190m，tc=0.0098m，l=0.0046m，b=0.0083m，阻尼通道宽度1mm，缸筒壁厚5mm，在ANSYS中建模仿真，得到阻尼通道平均磁感应强度曲线如图9所示。可以看出，磁流变减振器阻尼通道处的磁感应强度在0.628～0.679T之间，平均值在磁流变液工作磁感应强度0.6～0.65T范围内。

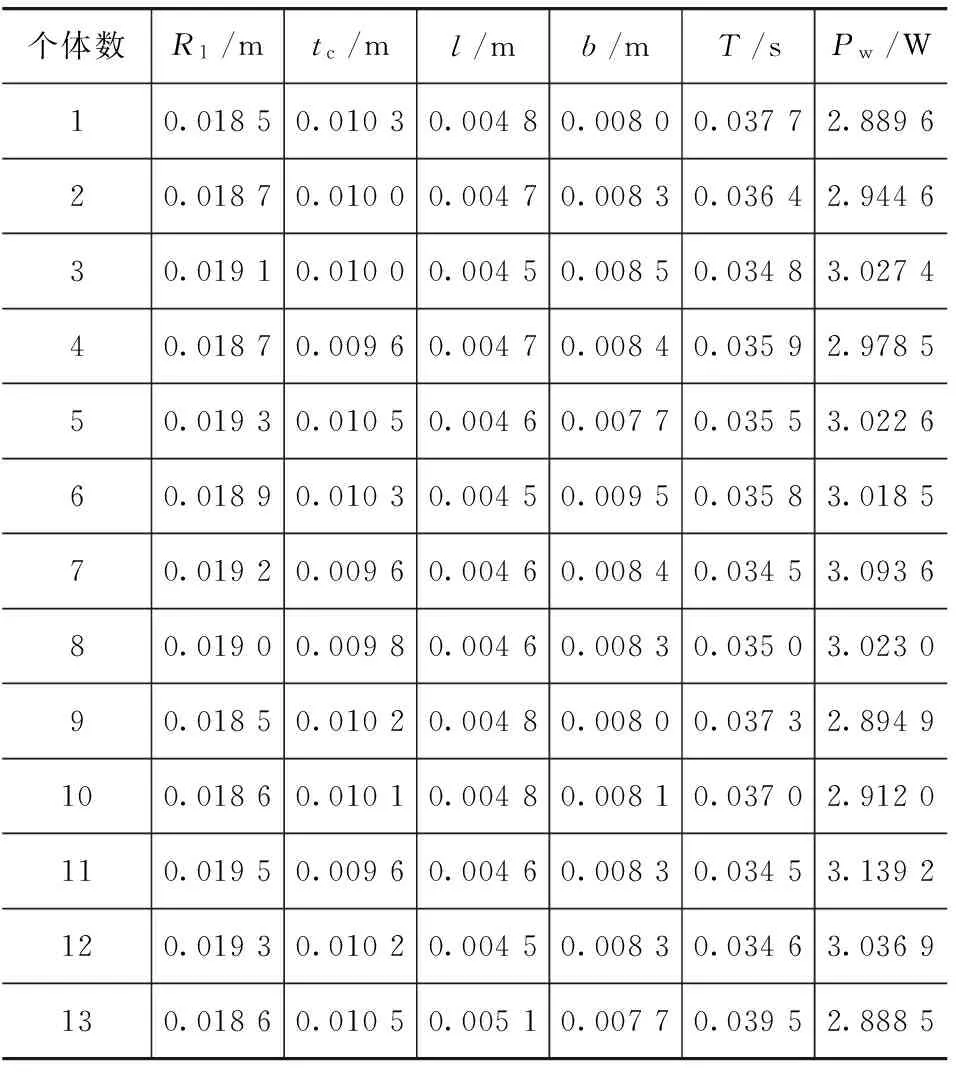
个体数R1/mtc/ml/mb/mT/sPw/W10.01850.01030.00480.00800.03772.889620.01870.01000.00470.00830.03642.944630.01910.01000.00450.00850.03483.027440.01870.00960.00470.00840.03592.978550.01930.01050.00460.00770.03553.022660.01890.01030.00450.00950.03583.018570.01920.00960.00460.00840.03453.093680.01900.00980.00460.00830.03503.023090.01850.01020.00480.00800.03732.8949100.01860.01010.00480.00810.03702.9120110.01950.00960.00460.00830.03453.1392120.01930.01020.00450.00830.03463.0369130.01860.01050.00510.00770.03952.8885

图10为优化前后的磁流变减振器结构内磁感应强度的分布云图。图10(a)中优化前的减振器磁感应强度最大值超过1.8T，远远超出活塞杆材料的饱和磁感应强度，而优化后的图10(b)中最大磁感应强度集中在饱和磁感应强度高的活塞头部分，活塞杆部分的磁感应强度没有超过规定的1.6T。

根据推导出的式(8)和式(9)输出阻尼力可得优化后的磁流变减振器输出阻尼力大小及范围，如表4所示。

表4 优化后磁流变减振器输出阻尼力

表5为优化前后目标函数值和尺寸参数对比，优化后的磁流变减振器消耗功率和响应时间分别降低了19.9%和15%，活塞头直径减小2mm，优化效果显著。

表5 优化结果及其对应的尺寸参数对比

5 结论

本文中根据磁流变减振器的工作特性，建立了磁流变减振器的结构优化模型，采用ANSYS参数化设计语言APDL，以流动模式磁流变减振器为例，对磁流变减振器进行了结构优化，得到如下结论。

(1)以线圈功率消耗和响应时间为目标函数，输出阻尼力和减振器各处磁感应强度为约束条件，建立的优化模型能使磁流变减振器在满足各约束条件下，降低电磁线圈功率消耗，缩短响应时间，同时改善磁流变减振器的静、动态特性。

(2)优化后磁流变减振器的线圈功率消耗减少19.9%，时间响应降低15%，表明优化流程与优化程序正确，迭代过程收敛。

[1] 王冰，韩冰源，王岩，等. 汽车磁流变减震器研究综述[J]. 森林工程，2008, 24(4): 39-43.

[2] 徐晓美，张明刚，曾才民. 磁流变液风扇离合器的设计与分析[J]. 工程机械，2010, 41(1):30-33.

[3] 蒋科军，刘成晔. 车用磁流变液制动器制动效果分析与研究[J]. 拖拉机与农用运输车，2009,36(6):25-27.

[4] 关新春，欧进萍.磁流变耗能器的阻尼力模型及其参数的确定[J].振动与冲击，2001,20(1):5-8.

[5] 李锐，陈伟民，廖昌荣，等. 基于磁流变技术的发动机隔振控制[J].机械工程学报，2009,45(3):183-190.

[6] 黄豪彩，黄宜坚. 磁流变技术及其在机械工程中的应用[J].制造技术与机床，2003(4):24-26.

[7] CARLSON J D, et al.Magnetorheological fluid damper: 5277281[P], 1994.

[8] 于学华，彭来森. 汽车磁流变悬架技术进展[J]. 新技术新工艺，2009(8):19-21.

[9] CARLSON J D,CATANZARITE D M, ST CLAIR K A. Commercial magneto-rheological fluid devices[J]. International Journal of Modern Physics B, 2012, 10(10):2857-2865.

[10] 郑玲,兰晓辉,李以农. 基于组合目标函数的磁流变减振器优化设计[J]. 振动工程学报,2011,24(6):600-606.

[11] 苏富强. 汽车悬架磁流变减振器的优化设计及仿真[J]. 机电工程,2007,24(7):22-25.

[12] 祝世兴,卢铭涛. 磁流变减振器磁路结构的参数化优化设计[J]. 机械设计与制造,2013(3):41-45.

[13] NGUYEN Q H, HAN Y M, CHOI S B, et al. Geometry optimization of MR valves constrained in a specific volume using the finite element method[J]. Smart Materials and Structures, 2007, 16(6):2242-2252.

[14] NGUYEN Quoc-Hung, CHOI Seung-Bok. Optimal design of a vehicle magnetorheological damper considering the damping force and dynamic range[J]. Smart Materials and Structures, 2009, 18(1): 1-10.

[15] CHOI S B, NGUYEN Q H, WERELEY N M. Optimal design of magnetorheological valves via a finite element method considering control energy and a time constant[J]. Smart Material and Structures, 2008, 17(2): 1-12.

[16] 隋莉莉，欧进萍. 半主动磁流变减振驱动器的工作原理及应用[J].哈尔滨建筑大学学报， 2002, 35(3):9-13.

[17] GOLDBERG D E. Genetic algorithm in search, optimization and machine learning[M]. New York: Addison-Wesley, 1989:152-154.

[18] 阮宏博.基于遗传算法的工程多目标优化研究[D].大连：大连理工大学，2007.

[19] 肖晓伟,肖迪,林锦国,等.多目标优化问题的研究概述[J]. 计算机应用研究，2011,38(3):805-808.

[20] 郑强.带精英策略的非支配排序遗传算法的研究与应用[D].杭州：浙江大学，2006.

Multi-objective Optimization of Vehicle MR Damper Based on Genetic Algorithm

Zheng Ling1,2, Niu Boyao1, Li Yinong1,Pang Jian2,3, Li Chuanbing2,3, Xu Xiaomin2,3& Fu Jianghua2,3

1.CollegeofAutomobileEngineering,ChongqingUniversity,StateKeyLaboratoryofMechanicalTransmission,Chongqing400044；2.StateKeyLaboratoryofVehicleNVHandSafetyTechnology,Chongqing401120； 3.Chang′anAutomobileResearchInstitute,Chongqing401120

To meet the functional requirements of vehicle semi-active suspension system, it is appropriate to design a magneto-rheological (MR) damper with low energy consumption, quick response and a wide adjustable range of damping force. In this paper, a multi-objective optimization model for MR damper is set up and NSGA-II algorithm is adopted to conduct a multi-objective optimization for MR damper, with its power consumption in coil and response time as objectives, and its output damping force and magnetic induction intensity at damping channel as constraints. An optimal Pareto solution set is then obtained and the results show that multi-objective optimization not only met the engineering requirements on the adjustable range of damping force, but also greatly reduce the power consumption in coil and significantly shorten response time, so providing an effective method for the structural optimization of MR damper.

MR damper; NSGA-II algorithm; multi-objective optimization

*汽车噪声振动和安全技术国家重点实验室开放基金(NVHSKL-201405)和国家自然科学基金(51275541)资助。

原稿收到日期为2015年1月22日。