铁路网瓶颈区段动态车流推算及运力资源分配优化方法

王　龙，林柏梁，马建军，闻克宇

(1.中国铁路经济规划研究院 运输研究所，北京　100038；2.北京交通大学 交通运输学院，北京　100044；3.中国铁路总公司 运输局，北京　100844)

随着高速铁路的逐步建成通车，与高速铁路并行的既有线的货运能力获得了一定程度的释放，大部分区段的通过能力基本可以满足其运量需求，然而，仍有少部分区段一直处于超负荷运输状态，成为阻碍路网车流运输顺畅的瓶颈区段。

在“实货制”的铁路货运组织模式下，货主的装车需求以“实货”为基础，这就为瓶颈区段车流的有效推算创造了条件，然而如何准确推算出瓶颈区段的动态车流量及其车流时空结构，成为合理制定调度决策的关键。同时，如何将瓶颈区段有限的运力资源分配给各装车需求，对于实现货运装车综合效益最大化具有重要意义。

在铁路网车流推算方面，文献[1]提出了利用确报系统、货票系统、车号自动识别系统所提供的数据推算实时及中远期车流的基本思路，并论述了基于请求车系统推算铁路局管内运用车保有量及局间分界口排空流量的方法。文献[2]通过对列车工作计划、分界口出入车流等动态数据的实时处理实现了对铁路局管内日常车流的推算，以18点各铁路局装车去向数据为依据实现了远期接入自卸重车的流量推算。上述研究基本停留在推算一些具有轮廓性的宏观指标的研究层面，而在一些更为精细化的运输指标的推算方面存在明显的局限性。在装车需求优化受理方面，文献[3]综合考虑了请求车优先级、货运收益、当前货运任务系数、站段优先级等指标，并分析了承认车的资源能力限制条件，构建了承认车最优分配模型。文献[4]在文献[3]的基础上采用日期均衡、分配批次均衡和货运计划均衡对模型进行了修正和改进。文献[5]在日装车计划的基础上，考虑早6点调整计划必须解决的3个方面问题，对可变类型的请求车进行调整，建立了改进的日班计划调整模型。文献[6]建立了装车效益综合评价指标体系，并以装车综合效益最大化为目标给出了装车决策问题的数学描述。以上文献虽对影响承认车优化分配的相关因素进行了较为全面的分析，但其中关于承认车对于运能占用的约束表达缺乏动态性的考虑，往往导致运量负荷与资源能力难以有效匹配。

本文基于最远站法则依次获取车流的有调和无调中转作业地点，从而提出车流运输时间的精确推算方法，以此实现瓶颈区段动态车流的有效推算；采用动态资源分配思想，基于推算的瓶颈区段动态车流量及其构成，考虑影响承运装车的多项指标，建立瓶颈区段运力资源分配多目标规划模型，同时基于线性加权和法设计模型求解算法。

1　瓶颈区段动态车流推算

瓶颈区段动态车流推算，是指在决策基准时刻，根据所掌握的车流数据(包括在途重车车流和未来一段时间内的装车需求车流)，提取其中途经瓶颈区段的车流，通过计算其运输至瓶颈区段的时间，推算目标日期瓶颈区段的动态车流量及其结构。例如，假设在某年某月10日6:00推算该年该月15日瓶颈区段的车流时，决策基准时刻即为10日6:00、目标日期为15日，所考虑的车流数据包括10日6:00时路网中的在途重车，以及在10日6:00至15日18:00(即15日终止时刻)期间的装车需求。

1.1　车流分析

根据车辆状态，进一步细分在途重车车流和装车需求车流的种类如下。

(1)根据在途重车的运行或作业状态，可将其划分为如下3类。

①随列车在途中运行(包括在区间内运行和在中间站待避停留)的车流。

②在技术站进行技术作业(包括有调作业和无调作业)的车流。

③在装车站处于装车状态(包括正在装车和装毕待发)的车流。

(2)根据是否已经获得受理，装车需求车流分为如下2类。

①已获受理而尚未开始装车的车流。

②尚未受理的需求车流。

1.2　车流运输时间推算

首先，从广义角度分析铁路网中任意1股车流自开始装车至送达目的地的运输时间由3部分构成。分别为：①从开始装车到从装车站出发的停留时间T停；②在区段内的旅行时间T旅；③在沿途技术站的中转滞留时间T中(包括有调中转时间T有和无调中转时间T无)。

车流有调作业站点序列的判断需以列车编组计划为依据，通过分析编组去向的吸引范围确定车流沿途改编链。在此，本文采用文献[7]中阐述的最远站法则确定车流依次编入的直达去向，从而获取车流沿途进行有调作业的站点集合。车流随直达列车在技术站的无调中转作业主要为更换机车或乘务人员交接，所以本文参考文献[8]，以机车交路作为车流无调作业站点序列的推断依据。此处需要说明的是，通常情况下，车流的改编作业过程包含换挂机车等无调作业内容，所以若根据机车交路推算出车流进行无调作业的站点集合，那么其中必然已涵盖了进行有调作业的全部站点，因而在中转作业时间推算方面，只计入对应车站的有调中转作业时间。以图1为例，根据图中列举的编组去向和机车交路可以判断S1→S6车流的沿途有调作业站点为S3，无调作业站点依次为S2，S3，S4，因此在S1→S6车流运输时间的推算过程中，只计入S3站的有调中转时间。

图1　车流有调、无调作业站点序列示例

对于任意1股动态车流，其从决策基准时刻或从开始装车至送达瓶颈区段的运输过程，均可视为在该车流整个走行过程中截取的部分子过程，由此即可为推断动态车流从其所在位置至瓶颈区段所需的运输时间提供方法依据。

1)在途重车车流的运输时间

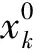
由此则有

(1)

推算得到每一类在途重车车流k送达瓶颈区段的运输时间Tk后，从基准时刻开始向后延伸时长Tk，即可推算出所有在途重车车流送达瓶颈区段的日期与时刻。

2)装车需求车流的运输时间

(2)

由于装车需求车流为尚未装车的潜在车流，而通过要车计划仅能获知开始装车的日期，具体的开始装车时刻尚不得而知。对此，可通过分析以往数日车流k的装车站取送车计划推算得到空车配送时刻的分布规律，进而给出货物开始装车时刻的合理取值，从装车时刻开始向后延伸时长Tk，即可推算出装车需求车流送达瓶颈区段的日期与时刻。

1.3　瓶颈区段动态车流及其结构的推算

在分别推算出每一股动态车流的运输时间及其送达瓶颈区段的日期后，即可反推出目标日期瓶颈区段的动态车流结构[9]。仍以10日6:00推算15日瓶颈区段动态车流为例，图2中共有5个车站的始发车流经过瓶颈区段。

图2　瓶颈区段动态车流结构简例

根据图2，形成目标日期(15日)瓶颈区段车流量的动态车流结构见表1，其中，在途重车由于已经装车，因而推算出的在途重车车流与实际较为吻合；装车需求车流中，已受理的部分亦为确切流量(若不考虑后续承运计划的修正)，而未受理的部分，将由于能力限制可能会有所削减。至于削减的程度大小，可依车流推算结论而定，同时为更进一步的瓶颈区段运力资源分配提供计算条件。

表1　简例中瓶颈区段动态车流结构

此外，不难发现，决策基准时刻距离目标日终止时刻的时长与车流运输时间的比对关系决定了“装车需求→在途重车”的转化关系，若运输时间大于此时长，则在基准时刻，相应的要车计划号必然已开始装车，由此，从动态角度来看，若使1次装车决策能够覆盖路网中全部相关装车地的货运需求，则决策基准时刻应具备足够的提前量。

2　瓶颈区段运力资源动态优化分配

既有的相关文献中对于优化承认车决策的研究[3-6]主要以合理制定次日的装车计划为目的，研究对象为次日装车的货运需求，而其中关于承认车对区段通过能力占用限制的表达缺乏动态性的考虑，导致运量负荷与区段通过能力难以有效匹配。本文基于推算的动态车流，将瓶颈区段的运力资源限额分配给各个装车需求，从而使得推算出的目标日期瓶颈区段运量负荷与其通过能力更加匹配。

2.1　瓶颈区段运力资源动态优化分配多目标规划模型

2.1.1装车需求限额承运的影响因素分析

装车需求限额承运决策的制定是一个复杂的问题，既要考虑货物运输的经济效益，又要兼顾社会效益，对此本文从如下若干方面探讨影响装车需求限额承运的效益指标，从而实现瓶颈区段运力资源的合理分配。

(1)经济效益：承运装车的经济效益主要体现为单车运输收入(即运费)与运输成本的差值。运费的主要影响因素表现为与货物品类相关的运价号及运输里程等，而运输成本主要包括货车使用费用、内燃和电力机车能耗费用等。通常，在经济效益最大化的驱使下，铁路运输更倾向于运距长且具有高附加值的货物。

(2)货物优先级：铁路运输的社会效益体现为货物装车的优先级。对于救灾和军用急需物资、国家重点物资以及指令性计划应予以优先装车，其他物资次之。对此，本文采用评分原则确定每一要车计划号的优先级指标，评分越高表明优先级越高。

(3)任务完成情况：目前铁路对大宗货物采用协议运输，实行月计划的受理方式；而对于非协议运输的零散货物，原则上敞开受理，随到随运，但由于瓶颈区段通过能力的限制，部分运输需求仍难以落实“随到随运”，需要在承运装车数量上进行删减，或者在受理日期上向后延伸。对此，本文利用任务系数来描述运输任务的完成动态。

对于大宗货物，设当月计划装车数为Qm，从月初至今已受理装车数为Qc，则其任务系数为

(3)

对于零散货物，参考前2日的要车受理情况，设计划日提报的要车数为λ0，计划日前1日的要车数和承运装车数分别为λ1和θ1，计划日前2日的要车数和承运装车数分别为λ2和θ2，则其任务系数为

(4)

(4)受理均衡性：在上述任意单一目标的驱使下，承运装车决策极易造成“两极分化”的分布态势，即瓶颈区段的运力资源更为集中地分配给单车效益指标较高的要车计划号，而其他客户的运输需求则很少甚至无法得到满足，从而造成铁路货源的大量流失。对此，本文将装车需求的不满足率作为1项考核指标引入装车需求限额承运决策，并以实现该指标的均衡分布为目标进行优化。

2.1.2模型假设

模型的构建基于如下假设。

(1)路网中除瓶颈区段外其余路段的通过能力均有富余。

(2)瓶颈区段的通过能力已扣除空车流占用的通过能力，即所考虑的通过能力约束仅表示重车通过能力。

(3)装车需求的优化受理暂不考虑空车能否有效配送的问题，在实际操作中可将此问题融合到模型的装车能力限制这一约束中。

2.1.3模型参数与变量定义

针对某个瓶颈区段，设其扣除空车流和当前在途重车流占用的通过能力后，可为潜在装车需求提供的剩余通过能力为B，基于车流推算结论，设N为在目标日期内到达瓶颈区段的要车计划号集合。令qn为第n(n∈N)个计划号提报的要车数，并定义决策变量xn为该计划号的受理车数，即为其所分配的瓶颈区段运力资源。

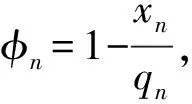
2.1.4模型构建

由此，综合考虑装车需求限额分配的多项效益指标，构建瓶颈区段运力资源动态优化分配的多目标数学规划模型Z如下。

(5)

(6)

(7)

(8)

s.t.

xn≤min{qn,ln}∀n∈N

(9)

(10)

(11)

在模型Z的目标函数中：式(5)表示承运装车的经济效益最大；式(6)表示承运装车货物的优先级最高；式(7)表示装车任务完成量最大；式(8)表示实现各个要车计划号的均衡分配。在模型Z的约束条件中：式(9)表示每个计划号承运装车数限制，即第n个计划号的承运装车数不得超过该计划号的装车需求数量和相应的装车能力的最小值；式(10)表示目标日期经过瓶颈区段的承运装车总量不得超过瓶颈区段的剩余通过能力；式(11)表示决策变量为非负整数。

2.2　求解算法

求解多目标规划模型Z的思路为：分别为每一目标函数赋以权系数，将多目标整合为单目标；以该单目标规划的解作为原多目标规划的解。该求解方法的难点是如何找到合理的权系数，使多个目标用同一尺度统一起来。对此，本文基于运筹学的线性加权和法[10-11]确定任意目标函数的权系数。设模型Z的4个目标对应的权系数分别为αi，且αi>0(i=1,2，3，4)，M为任意的常数(M≠0)，则整合后的单目标为

U(x)=max[α1Z1(x)+α2Z2(x)+α3Z3(x)-α4Z4(x)]

(12)

αi(i=1,2，3,4)的值由下述方程组确定：

(13)

其中，

Zij=Zj(x(i))i,j=1,2，3,4且i≠j

式中：x(i)为在任意单个目标函数及其式(9)—式(11)约束条件下求得的优化解。

由此可见，如何分别在任意单个目标下求得优化解x(i)，是本问题求解的关键。由于模型Z的前3个目标函数均为线性函数，所以，本文以其中任意1个目标函数结合约束条件式(9)—式(11)为单目标函数优化模型，设计1种“贪婪”式算法，求解单个目标函数优化模型的最优解x(i)。算法步骤如下。

Step 1：算法开始，设变量f为要车计划号集合N中的总计受理数量，即将在目标日经过瓶颈区段的潜在车流量，且f的初始值为0。

Step 2：遍历集合N，根据每一要车计划号n的经济收益(rn-cn)、货物优先级ωn、任务系数δn，按照从大到小的顺序排序(序号依次为1,2,…)。

Step 3：设变量y表示依次取到的序号，p(y)表示序号y对应的要车计划号，p(y)∈N，y的初始值取1； 设zy表示序号y对应的要车计划号p(y)可受理车数的上限， 即zy=min{lp(y),qp(y)}。

Step 5：输出装车需求限额承运分配方案，算法结束。

基于上述算法流程，可分别计算得到x(1)，x(2)，x(3)。

由于模型Z的第4个目标函数式(8)为最小化的二次目标函数，因此，将其分解展开可得

(14)

可见，以式(15)为目标函数、以式(9)—式(11)为约束条件的单目标规划模型的形式与经典最优化理论中的二次规划问题完全相同。经典最优化理论中的二次规划问题模型(Z-q)为

(15)

s.t.

Ax≥b

(16)

x≥0

(17)

对于二次规划问题模型(Z-q)，采用Lemke方法[12]进行求解。

对应本文问题，H为|N|阶对称矩阵，c为|N|维0向量，A为(|N|+1)×|N|矩阵，A的质为|N|；采用Lemke方法计算可以得到以式(15)为单目标函数的二次规划最优解x(4)。

根据计算得到的x(1)，x(2)，x(3)，x(4)，由式(14)可计算得到Zij(i，j=1，2，3，4)，然后将其带入方程组式(13)进行求解，可得到模型Z中的权重系数αi(i=1，2，3，4)(由于αi的表达式过于复杂，在此不予罗列)。

将权重系数αi(i=1，2，3，4)的值带入式(12)，并以此为目标函数、以式(9)—式(11)为约束条件，从而将多目标规划模型Z转化为单目标规划模型，该单目标规划亦为形如模型(Z-q)的二次规划模型，仍可运用Lemke方法进行求解，此时，H仍为|N|阶对称矩阵，只是对应元素应分别乘以系数α4，c为|N|维列向量，并且ci=α1(ri-bi)+α2ωi+α3δi，其余参数不变。由此即可计算得到多目标规划模型Z的解。

3　实例分析

陇海线的洛阳东→铁炉区段为路网中能力紧张的典型瓶颈区段之一，该区段的日重车通过能力约为3 200车，本文以此为实例进行车流的推算和运力资源的分配。

以2013-11-10 T6：0：0为预测基准时刻，即以此刻的实时车流分布状态和所掌握的装车需求情况作为决策的初始条件，动态推算2013-11-15该区段的车流量。在假设尚未受理的装车需求全部作为潜在车流量并将其计入推算条件的前提下，经过对在途重车和装车需求车流运输时间的测算，预测得到2013-11-15洛阳东→铁炉区段的重车流量为5 462车，其中在途重车897车、装车需求4 565车(共涵盖306个要车计划号，限于篇幅，仅列举其中部分计划号，见表2)。可见，推算而得的2013-11-15瓶颈区段理论车流量超出通过能力达2 262车之多，即4 565车的装车需求中，最多只能有2 303车得到满足。

将相关参数带入优化模型，基于线性加权和法计算得到模型Z中各目标的权重系数分别为：α1=0.000 006 2,α2=0.001 221 5,α3=0.304 472 6,α4=0.694 299 7，再将其带入式(12)进行单目标规划模型求解，从而获取多目标规划模型的优化解，即瓶颈区段运力资源动态分配方案，对应表2给出部分决策方案，详见表2中的承运装车数。

以表2中序号为16的拟定于2013-11-13由胡集站装车发往绥化站的一股车流为例进行分析，该要车计划号的装车需求车数为5车，经测算，由装车站胡集至瓶颈区段入口站洛阳东站的运输时间为40.66 h，则预计该股车流将于2013-11-15运抵瓶颈区段，从而成为构成此日瓶颈区段流量负荷的潜在流量之一。在对目标日期(2013-11-15)瓶颈区段的运力资源进行优化分配时，考虑到该要车计划号的单车收益较高、优先级较低、任务系数适中等因素，综合考虑各项效益指标，为该计划号分配4辆承运车，即在瓶颈区段2 303车的剩余运能中将有4车的运力资源分配给该装车需求。

对优化获取的瓶颈区段运力资源分配方案进行总体分析可知：方案共计承运装车2 303车，分布于279个要车计划号，即有27个计划号完全落空；装车需求的平均满足率为81.8%，其中只有204个计划号的装车需求得到了完全满足；相关的承运装车决策将创造1.68×107元的经济收益，虽然较理论上的最大收益减少了0.58×107元，但承运货物的优先级得到了保证，并且兼顾了任务受理的完成情况，装车需求限额承运分配更具时空均衡性；此外，具有动态特性的瓶颈区段运力资源分配方案也将使得瓶颈区段的运量负荷与其通过能力更加匹配。

4　结　论

本文针对路网中的瓶颈区段，基于决策基准时刻的在途重车和未来一定时间内的装车需求数据，动态推算瓶颈区段未来某一目标日期的潜在流量负荷；考虑到装车需求的完全受理将给瓶颈区段带来超负荷的运输压力，综合考虑多项效益指标，对将于同一目标日期内送达瓶颈区段的装车需求进行限额受理，构建瓶颈区段运力资源动态优化分配多目标规划模型，并基于运筹学的线性加权和法设计模型的求解算法，实现了瓶颈区段运力资源的优化分配，平衡了运量与通过能力的适应关系。以陇海线瓶颈区段洛阳东→铁炉区段为实例，验证了瓶颈区段车流推算及运力资源分配优化方法的合理性与有效性。今后，在车流运输时间参数设定方面，如何基于随机理论将影响车流运行的各种不确定因素融入车流作业时间的参数设定之中，还有待于进一步的研究。

[1]李晓海. 铁路运输调度车流推算辅助决策系统[J]. 中国铁路，2011 (1):58-60.

(LI Xiaohai. Decision Support System for Train Flow Calculation in Railway Dispatching[J]. Chinese Railway, 2011(1):58-60. in Chinese)

[2]范英书，崔增仁，林郁山，等. 铁路局运输调度车流推算及调整系统[J]. 中国铁路，2009(2):10-12,15.

(FAN Yingshu, CUI Zengren, LIN Yushan, et al. Traffic Flow Estimation and Adjusting System for Traffic Dispatching in Railway Administrations[J]. Chinese Railways, 2009(2):10-12,15. in Chinese)

[3]江南，史峰，任少卿. 铁路承认车最优分配模型与算法研究[J]. 铁道学报，2005,27(5):19-23.

(JIANG Nan, SHI Feng, REN Shaoqing. The Optimal Model and Algorithm for Approved Rail Car Allocation[J]. Journal of the China Railway Society, 2005, 27(5):19-23. in Chinese)

[4]江南，史峰，玉清，等. 铁路承认车均衡审批模型及算法[J]. 中国铁道科学，2008,29(4):121-126.

(JIANG Nan, SHI Feng, YU Qing，et al. The Equilibrium Approving Model and Algorithm of Rail Approved Car[J]. China Railway Science, 2008,29(4):121-126. in Chinese)

[5]江南，宰停，韦成燕，等. 铁路承认车早6点调整计划优化模型及算法[J]. 中国铁道科学，2007,28(3):117-121.

(JIANG Nan, ZAI Ting, WEI Chengyan, et al. The Optimal Model and Algorithm of 6am Adjustment Plan for Rail Approved Car[J]. China Railway Science, 2007,28(3):117-121.in Chinese)

[6]李文庆. 铁路装车效益综合评价及智能决策问题的研究[D]. 北京：北京交通大学，2005.

(LI Wenqing. Research on Rail Loading Benefit Evaluation and Intellectual Decision Problem[D]. Beijing: Beijing Jiaotong University, 2005. in Chinese)

[7]林柏梁，田亚明，王志美. 基于最远站法则的列车编组计划优化双层规划模型[J]. 中国铁道科学，2011,32(5):108-113.

(LIN Boliang, TIAN Yaming, WANG Zhimei. The Bi-Level Programming Model for Optimizing Train Formation Plan and Technical Station Load Distribution Based on the Remote Re-Classification Rule[J]. China Railway Science, 2011, 32(5):108-113. in Chinese)

[8]林柏梁.机车长交路条件下的技术站列车编组计划无调作业参数模型[J].铁道学报，1999,21(6):6-9.

(LIN Boliang. Non-Resort Operating Parameter Model for Technical Station’s Train Formation Plan with Locomotive Extended Routing[J]. Journal of the China Railway Society, 1999,21(6):6-9. in Chinese)

[9]林柏梁. “实货制”条件下铁路网瓶颈区段流量动态推算技术[R]. 北京：北京交通大学，2015.

[10]甘应爱，田丰，李维铮，等. 运筹学[M]. 北京：清华大学出版社，2005.

[11]MARLER R T, ARORA J S. The Weighted Sum Method for Multi-Objective Optimization: New Insights[J]. Structural and Multidisciplinary Optimization, 2010,41(6):853-862.

[12]陈宝林. 最优化理论与算法[M]. 北京：清华大学出版社，2005.