基于视觉测量的太阳翼模态参数在轨辨识*
2016-04-10吴小猷李文博张国琪
吴小猷,李文博,张国琪,关 新,郭 胜,刘 易
(1.北京航空航天大学,北京100191;2.北京控制工程研究所,北京100190)
学术研究
基于视觉测量的太阳翼模态参数在轨辨识*
吴小猷1,李文博2,张国琪2,关 新2,郭 胜1,刘 易1
(1.北京航空航天大学,北京100191;2.北京控制工程研究所,北京100190)
针对传统接触式振动测量方法的缺点,提出一种基于视觉测量的太阳翼模态参数在轨辨识方法.具体过程包括相机标定、标志点检测、三维坐标解算和模态辨识等.利用两台相机和一台计算机构成的双目立体视觉测量系统进行了地面试验,测量得到了太阳翼测点处的振动位移响应,然后采用ERA算法辨识出了真实太阳翼的两阶主要模态参数.通过与激光测振仪测量结果进行比较,验证了上述方案的有效性.实验表明,视觉测量方法设备简单,灵活性高,是一种理想的在轨振动测量方法.
模态辨识;视觉测量;太阳翼;振动测量
0 引言
为满足现代航天应用技术对航天器提出的更高性能、更大功率与更大容量等发展需求,同时受发射质量与体积的制约,带轻质超大型复杂可展开挠性结构的航天器已成为现代大型航天器的发展趋势.超大型空间挠性结构由于其结构复杂,自身刚度低,一般具有低频模态密集和模态阻尼比很小的特点.此类结构在阻尼很小的空间环境中,一旦受到外界扰动激励,便会引起长时间振动且难以衰减,从而影响卫星姿态稳定,甚至导致星上有效载荷无法正常工作.为了对这类对象进行有效的振动控制,需要首先了解其动力学参数,即固有频率、振型、阻尼等.但由于此类对象呈现出复杂的非线性多体运动特性,对这类航天器进行理论或有限元精确建模非常困难.而采用地面试验建模的方式获取这类对象的模型受到地面重力、卸载条件、空气阻尼以及试验环境的影响,所得到的模型参数与在轨参数相比仍存在较大差异.因此,为可靠地获取这类对象的动力学模型参数,提高控制器设计的品质,开展此类航天器在轨辨识技术的研究,意义非常明显[1-2].
为获取结构的振动响应数据用于模态辨识,可采用接触式测量和非接触测量两种测量方式.传统模态参数辨识一般是基于接触式测量方法,采用压电陶瓷、加速度传感器和陀螺仪等获取振动信息[3-5].这种接触式测量方法不仅存在信号迟滞、对噪声敏感、温漂等问题,还会给太阳翼等轻质结构带来附加的质量和约束,影响其动态性能和测量结果.而非接触测量作为近年来新兴的一种振动测量方式,具有对被测结构无损伤,不影响其动态性能和正常工作,以及降低传感器带来的在轨设备复杂度和成本等优点.在各类非接触测量方法中,视觉测量还具有高灵活性,低成本,大范围同步测量等优点,是一种理想的复杂大挠性结构在轨振动测量方法.
1996年,NASA首次将视觉摄影测量应用于航天器挠性附件模态参数辨识.试验时通过航天飞机搭载摄影测量设备对和平号空间站的太阳能帆板进行了模态测试[6],以帆板边缘上的角点作为测点,成功辨识出了太阳能帆板的在轨模态参数.1998年,NASA仍采用太阳帆板的边缘角点作为检测点,利用摄像测量法获得了不同环境下哈勃望远镜太阳翼的变形信息[7],并在此基础上开展了模态辨识实验.国内尚未见到利用视觉测量进行挠性航天器在轨模态参数辨识的在轨试验报道,目前还处于理论研究和地面试验仿真阶段[8-10].
本文提出了一种基于视觉测量的太阳翼模态参数在轨辨识方法,通过由两台相机和一台计算机构成的双目立体视觉测量系统测量太阳翼测点处的振动位移,再利用振动位移辨识得到所需的模态信息.与NASA基于角点检测的摄影测量方法不同,本文在太阳翼表面布置圆形标志点作为测点,通过标志点检测技术获取测点处的振动位移信息.具体过程包括相机标定,标志点检测,三维坐标解算和模态辨识等.通过搭建由真实太阳翼、两台测量相机和一台计算机等组成的物理试验仿真系统,开展了面向在轨辨识的地面仿真实验,成功辨识出了太阳翼的两阶主要模态参数,验证了所述方案的正确性和有效性,为中国未来航天器大型挠性结构模态参数在轨辨识积累了初步的技术基础.
1 双目视觉测量技术
双目立体视觉是机器视觉领域中的一项重要技术.采用双目立体视觉能实现对运动物体的实时测量,从而达到在线检测的目的.双目立体视觉系统由左右两台相机和一台计算机组成,通过检测物体在左右相机中的成像差异计算物体在相机坐标系中的三维坐标.双目视觉测量技术主要包括:相机标定、标志点检测和三维坐标解算.
1.1 相机标定
相机标定主要包括两部分:相机内参数标定[11]和相机外参数标定.相机内参数标定获取相机的畸变参数和内参数矩阵;相机外参数标定获取相机坐标系之间、相机坐标系与世界坐标系之间的旋转和平移矩阵.相机畸变参数用于矫正相机成像中存在的径向畸变和切向畸变,相机内参数矩阵用于建立图像坐标系和相机坐标系之间的相对位置关系;相机外参数用于建立相机坐标系之间、相机坐标系与世界坐标系之间的相对位置关系.
1.2 标志点检测
由于太阳翼尺寸较大,因此相机的成像距离较远,翼上的局部细节信息无法清晰投影到相机成像平面上.本文采用圆形标志点作为靶面,取标志点中心为检测点,检测标志点在相机图像上的成像区域,通过对该区域进行椭圆拟合求取标志点中心,进而解算出检测点的三维坐标.与角点检测的方法相比,具有检测精度高、抗干扰性强等特点.
当圆形靶点贴在太阳翼上时,会与太阳翼上太阳能电池阵列的网格纹理交叉,影响靶点轮廓的提取.本文首先采用灰度形态学方法[12],滤除了图像上靶点邻域的干扰纹理;然后使用大津阈值[13]对图像进行分割,滤除图像中的干扰轮廓,得到靶点轮廓;最后采用最小二乘法对轮廓进行椭圆拟合,得到标志点图像坐标见图1.

图1 标志点检测流程图Fig.1 Marking point detection flow
1.3 三维坐标解算
通过标志点检测算法能够获得标志点在左右相机图像坐标系中的像素坐标,根据标志点在左右相机中的像素坐标和图像坐标系和相机坐标系之间的相对位置关系即相机内参数,能够获得标志点在左右相机中的反投影射线.根据左右相机之间的相对位置关系,将其中一个相机中的反投影射线转换到另一个相机坐标系下,计算两条射线的交点即为标志点在相机坐标系下的三维坐标.最后,根据相机坐标系和世界坐标系之间的相对位置关系即可获得标志点在世界坐标系下的三维坐标.
综上所述,利用视觉测量法测量太阳翼等在轨挠性结构振动的步骤可以总结如下:(1)分别对左右相机进行内外参数标定;(2)使用相机对振动结构进行拍摄并对图像进行存储;(3)分析图像并利用标志点检测算法获得测点的像素坐标;(4)利用三维坐标解算方法获得测点的世界坐标;(5)利用测点不同时刻的世界坐标获得其位移振动曲线.
2 模态辨识算法理论
在通过双目视觉测量系统获得太阳翼测点处的振动位移响应后,便可以输入辨识算法进行模态参数辨识.本文采用的辨识算法是特征系统实现算法ERA[14].其基本思想是根据系统的脉冲响应,构造Hankel矩阵,然后对该 Hankel矩阵进行奇异值分解,通过奇异值分解的结果得到该系统的最小实现,系统的动力学参数就可以从最小实现系统矩阵中提取.其基本流程可阐述如下.
(1)根据脉冲响应数据构建Hankel矩阵
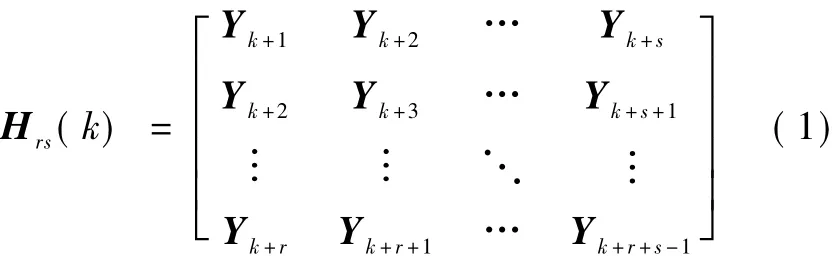
式中Y为系统的Markov参数.
(2)对Hrs(0)进行奇异值分解
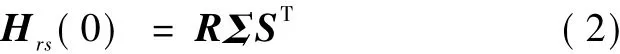
式中,Σ是Hrs(0)的奇异值降序对角阵,R和 S为左右奇异值向量矩阵.
(3)计算系统最小实现矩阵为

对 A^进行特征系统分解,就可以得到系统的频率、阻尼比、振型及模态幅值相干系数[15]等动力学参数.
3 仿真实验
为了验证上述方案的可行性,着手搭建了由真实太阳翼、两台测量相机和一台计算机等组成的物理实验仿真系统.
实验系统如图2所示,太阳翼由3块链接在一起的1 000 mm×2 000 mm碳纤维板组成,通过桁架固定在距离模型星体表面1 000 mm处.相机选择分辨率为2 048×2 048,帧率为90帧/s,具有全局快门和外部触发的工业相机.相机安装在距离桁架1 700 mm星体边沿处,相机之间的间距为1 724 mm.在测点处(中心黑点处)粘贴直径为40 mm的3 M圆形反光膜,调节相机角度使左右相机的立体视场包含太阳翼上的整个检测区域,然后调节相机光圈和焦距使整个测量区域在相机景深范围内.

图2 实验模型示意图Fig.2 Schematic diagram of experimental model
试验步骤如下:
(1)采用尺寸为1 000 mm×1 000 mm的黑白相间棋盘格对相机进行标定,如图3所示.标定时,左右相机分别获得棋盘格在不同指向平面内的9张图像,然后提取每张图像中的内角点在左右相机中的像素坐标,根据角点的已知坐标,求解相机的内参数.
根据步骤1求得的左右相机内参数矩阵M1, M2分别为:


图3 左右相机标定图像Fig.3 Calibration images of left camera and right camera
(2)保持相机位置不变,采集一帧太阳翼图像,然后计算出太阳翼上的点在相机坐标系下的三维坐标,再根据已知检测点在目标坐标系下的三维坐标,利用相机外参数标定方法求解相机的外参数.
按照步骤2标定获得的左右相机外参数矩阵W1,W2分别为:
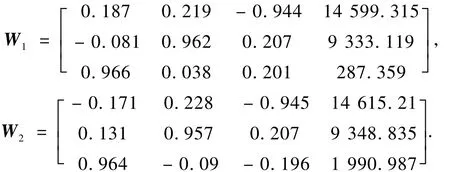

图4 测点1、2、4、5、6、7、8、9、10的Z轴方向振动位移曲线Fig.4 Vibration displacement curves of making point 1,2,4,5,6,7,8,9,10
(3)保持相机位置不变,调节相机焦距与曝光时间,设置相机的触发模式为外部同步触发,设置采集存储帧率为50帧/s.
(4)在测点1处将太阳翼末端拉偏,同时触发相机开始采集.对采集的图像进行保存,用于后续的分析处理.
(5)对采集的图像进行标志点检测,然后利用三维坐标解算方法得到每个测点的在目标坐标系下的三维坐标及Z轴方向的振动位移曲线,其中Z轴为垂直于太阳翼平面的方向.图4给出了视觉测量得到的测点1、2、4、5、6、7、8、9、10的Z轴方向振动位移曲线.
为了检验视觉测量结果的精度,将测点3处视觉测量结果与激光测振仪测得的结果进行对比,并给出两者的相对误差曲线,如图5所示.

图5 视觉测量结果与激光测振仪结果对比Fig.5 Results comparison between visual measurement and laser measurement
分析结果可知,视觉测量结果与激光测振仪测得的结果基本一致,平均绝对测量误差仅0.461 mm,最大相对误差不超过2.6 mm,满足测量精度要求.
(6)将上述10个测点的振动位移响应输入ERA算法进行辨识,得到Hankel矩阵的奇异值分布曲线如图6.
由奇异值曲线初步判定系统阶次为5,其中有一阶为虚假模态,将其剔除后可得到系统真实模态频率和阻尼比.将辨识得到的太阳翼模态参数与激光测振仪测得的结果比较如表1所示.
可以看出,太阳翼的固有频率很低,且在1点处将其拉偏时只能明显激发出两阶模态振动.而采用基于视觉测量的模态参数辨识方法可以有效辨识出真实太阳翼的这两阶模态参数,与激光测振仪测得的结果相比,各阶频率相对误差不高于3%,各阶阻尼比相对误差不高于11%,总体辨识结果理想.
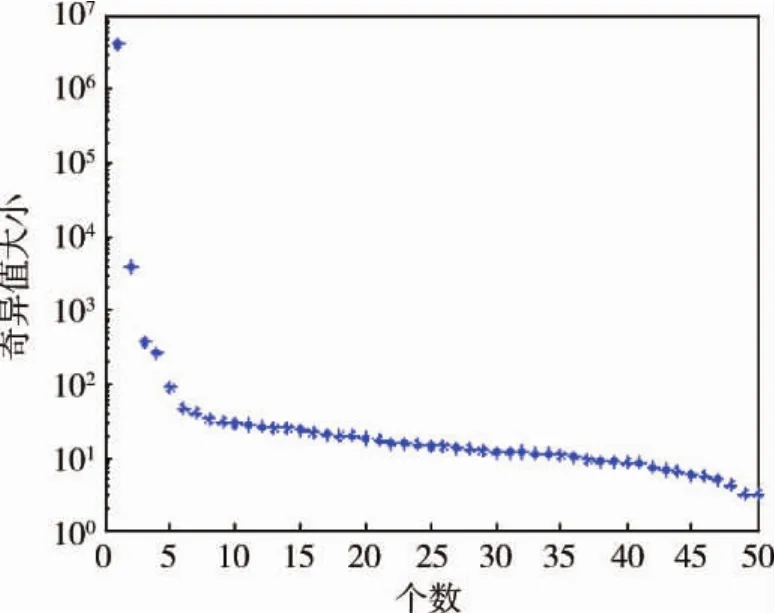
图6 Hankel矩阵的奇异值分布曲线Fig.6 The singular value distribution curve of Hankel matrix

表1 ERA算法辨识结果与激光测振仪结果对比Tab.1 Identification results comparison between ERA and laser measurement
4 结论
针对太阳翼模态参数在轨辨识问题,本文提出了一种基于视觉测量的太阳翼模态参数在轨辨识方法.首先,对两台相机进行内外参数标定,然后采集得到太阳翼测点处的动态图像,通过标志点检测算法获得测点的图像坐标,再利用三维坐标解算方法得到每个测点的三维坐标和Z轴方向的振动位移曲线,最后将振动位移响应输入辨识算法,辨识得到所需的模态信息.利用两台相机、一台计算机构成的双目立体视觉测量系统和真实太阳翼进行了地面试验,得到了真实太阳翼的两阶主要模态参数.试验表明,本文提出的基于视觉测量的模态参数辨识方法可以有效地对太阳翼等大型挠性结构进行在轨模态参数辨识.该方法不仅设备简单,而且测量灵活性很高,是一种理想的在轨振动测量方法.
[1]周舟,陆秋海,任革学.低密频太阳能帆板动力学参数在轨辨识和振动控制[J].工程力学,2004(3):84-89.ZHOU Z,LU Q H,REN G X.On-orbit identification and vibration control for solar arrays with low and close frequencies[J].Engineering Mechanics,2004(3):84-89.
[2]赵发刚,周徐斌,申军烽,等.航天器在轨模态辨识技术的探讨[C]//国际功能制造与机械动力学会议.杭州:中国振动工程学会,2011.
[3]刘泊,郭建英,孙永全.压电陶瓷微位移驱动器建模与控制[J].光学精密工程,2013,21(6):1503-1509.LIU B,GUO J Y,SUN Y Q.Modeling and control for PZT micro-displacement actuator[J].Optics and Precision Engineering,2013,21(6):1503-1509.
[4]靳振宇,吴建德,范玉刚,等.基于MEMS加速度计的管道位移检测系统设计[J].传感器与微系统,2012,31(1):140-142.JIN Z Y,WU J D,FAN Y G,et al.Design of pipeline displacement detecting system based on MEMS accelerometer[J].Transducer and Microsystem Technologies,2012,31(1):140-142.
[5]成宇翔,张卫平,陈文元,等.MEMS微陀螺仪研究进展[J].微纳电子技术,2011,48(5):277-285.CHENG Y X,ZHANG W P,CHEN W Y,et al.Research development of MEMS micro-gyroscopes[J].Micronanoelectronic Technology,2011,48(5):277-285.
[6]GILBERT M G,WELCH S S,PAPPA R S,et al.STS-74/MIR photogrammetric appendage structural dynamics experiment preliminary data analysis[M].Langley Research Center:National Aeronautics and Space Administration,1997.
[7]SAPP C,CENTER L B J S.Photogrammetric assessment of the hubble space telescope solar arrays during the second servicing mission:final report[M].Johnson Space Center:National Aeronautics and Space Administration,1998.
[8]邱志成,张祥通.基于视觉的柔性结构振动测量及其控制[J].振动、测试与诊断,2012,32(1):11-16.QIU Z C,ZHANG X T.Vision-based vibration measurement and control of flexible structure[J].Journal of Vibration Measurement&Diagnosis,2012,32(1):11-16,157-158.
[9]张春芳.基于双目立体视觉的大型柔性结构在轨振动测量研究[D].哈尔滨:哈尔滨工业大学,2014.ZHANG C F.The on-orbit vibration measurement research of large-scale flexible structures based on binocular stereo vision[D].Herbin:Harbin Institute of Technology,2014.
[10]许畅,王聪,高晶波.基于摄像测量法的在轨柔性结构模态参数辨识[J].哈尔滨工业大学学报,2014,11:17-23.XU C,WANG C,GAO J B.Videogrammetric based modal identification of on-orbit flexible structures[J].Journal of Harbin Institute of Technology,2014,11: 17-23.
[11]ZHANG Z.A flexible new technique for camera calibration[J].Pattern Analysis and Machine Intelligence,IEEE Transactions on,2000,22(11):1330-1334.
[12]SERRA J.Image analysis and mathematical morphology[M].New York:Academic Press,1982.
[13]OTSU N.A threshold selection method from gray-level histograms[J].Automatica,1975,11(285-296):23-27.
[14]JUANG J N,PAPPA R S.An eigensystem realization algorithm(ERA)for modal parameter identification and model reduction[J].Journal of Guidance Control and Dynamics,1985,8(5):620-627.
[15]PAPPA R S,ELLIOTT K B,SCHENK A.Consistentmode indicator for the eigensystem realization algorithm[J].Journal of Guidance Control&Dynamics,1993,16(5):852-858.
Aiming at the disadvantages of traditional contact vibration measurement,an on-orbit modal parameters identification method is presented based on photogrammetry for solar arrays.The specific process includes camera calibration,marking point detection,3D coordinate calculation and modal identification.A binocular stereo vision measurement system made of two cameras and a computer are used for the ground test.The vibration displacement response of measuring points on solar array is obtained.ERA algorithm is used to identify the two main modal parameters of solar array.By comparing with the results measured by laser vibrometer,the effectiveness of the scheme is verified.The experiment shows that the photogrammetry is an ideal method in vibration measurement,which has high flexibility and requires for simple devices.
modal identification;photogrammetry;solar arrays;vibration measurement
V44
A
1674-1579(2016)03-0009-06
10.3969/j.issn.1674-1579.2016.03.002
Photogrammetry-Based on-Orbit Modal Identification of Solar Arrays
吴小猷(1993—),男,硕士,研究方向为航天器动力学与模态辨识;李文博(1984—),男,工程师,研究方向为航天器扰性结构辨识与振动抑制;张国琪(1978—),男,高级工程师,研究方向为控制理论与控制工程;关 新(1986—),男,高级工程师,研究方向为航天器动力学与控制;郭 胜(1991—),男,硕士,研究方向为图像融合与机器视觉;刘 易(1990—),男,硕士,研究方向为视频处理与机器视觉.
*国家自然科学基金资助项目(61403029).
2016-01-29
WU Xiaoyou1,LI Wenbo2,ZHANG Guoqi2,GUAN Xin2,GUO Sheng1,LIU Yi1(1.Beijing University of Aeronautics and Astronautics,Beijing 100191,China;
2.Beijing Institute of Control Engineering,Beijing 100190,China)
