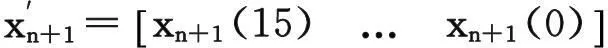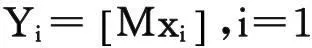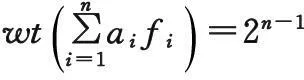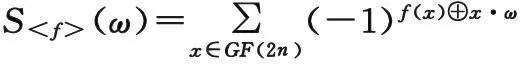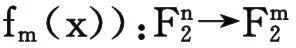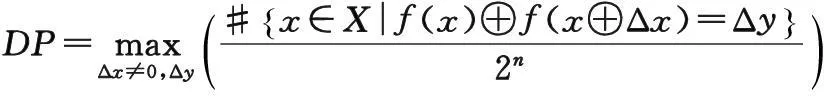分组密码中基于混沌映射的动态S盒构造

2016-04-09范明慧仰枫帆

无线电工程 2016年3期

关键词：信息安全

范明慧，仰枫帆

(南京航空航天大学电子信息工程学院，江苏南京 210016)

分组密码中基于混沌映射的动态S盒构造

范明慧，仰枫帆

(南京航空航天大学电子信息工程学院，江苏南京 210016)

摘要S盒是分组密码算法的唯一非线性部件，为了产生更加安全的动态S盒，提出了一种基于Logistic混沌映射和Tent混沌映射构造动态S盒的方法。在Logistic混沌映射的初值敏感性的基础上，生成的动态S盒是与密钥相关的。对S盒的双射性、非线性度、严格雪崩准则、输出比特间独立性、均匀差分性和灵敏度进行了测试和分析。各项理论分析和实验结果表明，该算法产生的动态S盒能够较好地符合各项设计准则，可以满足密码算法的安全性。

关键词S盒；混沌映射；分组密码；信息安全

A Method to Construct Dynamic S-box Based on Chaotic Map in Block Cipher

FAN Ming-hui,YANG Feng-fan

(CollegeofElectronicandInformationEngineering,NanjingUniversityofAeronauticsandAstronautics,NanjingJiangsu210016,China)

AbstractS-box is the only nonlinear component for block cipher algorithm.To generate more secure dynamic S-box,a method is proposed to construct S-box dynamically by two chaotic maps(Logistic and Tent chaotic maps).On the basis of the sensitivity to initial condition of Logistic chaotic map,the generated dynamic S-box is key dependent.Then the performance indices of S-box are summarized.Six properties,such as bijective property,nonlinearity,strict avalanche criterion,output bits independence criterion,equiprobable input/output XOR distribution and sensitivity,are tested and analyzed.Simulation tests show that the criterion for designing good S-box can be met approximately.The S-box can satisfy the security of the cryptography.

Key wordsS-box;chaotic map;block cipher;information security

0引言

在分组密码中，S盒为分组密码算法提供了混乱的作用，是分组密码设计的关键。近年来的研究表明，由于混沌理论系统具有很好的安全特性，如对初值和参数的敏感性、类随机性等特点，利用混沌映射构造的S盒取代传统S盒成为主流。

2001年，Jakimosk和Kocarev[1]首次提出了利用混沌映射构造出S盒的方法。该方法给出了一种基于离散化Logistic映射的混沌S盒。但是文献[1]仅仅分析了S盒的非线性度和差分均匀度。2009年，文献[2]中提出了一种新的基于连续混沌映射的动态S盒。由于混沌映射是连续的，因此需要进行离散采样。

本文提出一种新的基于离散混沌映射的算法构造动态S盒。以密钥作为Logistic映射的初值生成初始S盒，再以Tent映射生成的整数对对S盒进行置乱。由于该S盒由混沌映射的初值和控制参数决定，可以通过改变混沌映射的初值和控制参数产生不同的S盒。

1混沌原理

Logistic混沌映射[3]的数学表达式为:

xn+1=μxn(1-xn)。

(1)

虽然Logistic映射是简单的一维混沌映射，但是却能产生非常好的混沌行为，所以在相关研究中经常选取Logistic映射为研究对象。

Tent混沌映射是分段式一维映射，数学描述为:

xn+1=μmin(xn,1-xn)。

(2)

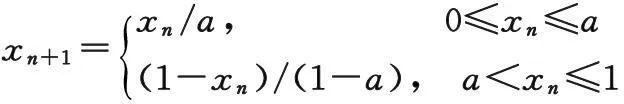
(3)

在不同的控制参数a下，斜Tent映射均处于混沌状态。

2基于Logistic-Tent映射的S盒构造

将混沌函数应用于8×8动态S盒的生成，总体流程分为2部分：

第1部分：首先将Logistic映射的参数设置为4，再以密钥作为Logistic映射的初始值。对于不同的密钥，生成的混沌序列是不同的，由此实现了动态S盒的产生。具体的算法步骤如下：

① 将密钥映射为混沌函数的初值：x0=K。其中x0为Logistic映射的初值，K为128 bit的初始密钥；

② 将x0带入混沌函数，其混沌函数为Logistic映射转化为大整数的形式。其数学表达式为：

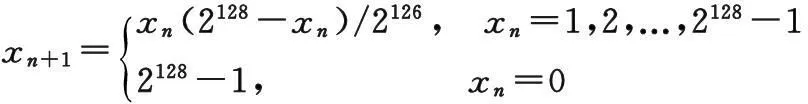
(4)

式中，0

③ 将128 bit的值xn+1按字节分组，共16 byte，xn+1=xn+1(0)xn+1(1)...xn+1(15)；

④ 将上述16 byte按位异或，得到1 byte的输出Y(i)，其中0≤i≤255，Y(i)=xn+1(0)⊕...⊕xn+1(15)，Y(i)∈(0,255)；

⑥ 依次将Y(i)放入S盒中，若Y(i)=Y(j)，j>i，i,j为自然数，则舍去Y(j)，若S盒的256个数值尚未填满，返回步骤②；若S盒已填满，则S盒生成结束。

第2部分：使用斜Tent映射对初始S盒进行置乱，得到满足一定非线性指标和差分均匀度的动态S盒。具体步骤如下：

① 设置斜Tent映射的参数a∈(0,1)和初始值x0∈(0,1)；

② 计算斜Tent映射的混沌迭代方程，得到长度为n的实数序列x1,x2,...,xn；

④ 根据G(i)交换S盒Yi和Yi+n/2位置上的元素，得到新的S盒，计算该S盒的非线性度和差分均匀度，若满足所设置的门限要求，则S盒生成结束；否则令i=i+1，继续步骤④；

至此，整个动态S盒的构造结束。

取Logistic映射的初值

x0=9C2B2E74D242D-8279398B9719E5AF043，

每轮运算中Logistic混沌映射迭代200次，经过1 511轮运算之后生成初始S盒；设置Tent映射初值x0=0.235 6，控制参数a=0.423 53，迭代步长n=2 000。设置门限要求：非线性度平均值不小于105，差分均匀度最大值为10，根据这1 000组随机整数，对初始S盒进行置乱，经过32次置换后得到8×8的S盒。下面给出S盒的部分数值：

3动态S盒性能分析与验证

S盒设计通常有5个准则：双射性、非线性度、严格雪崩准则、输出比特间独立性和差分均匀性。本文还对S盒进行了灵敏度分析，通过改变Logistic混沌映射的初值，即改变系统的密钥，判断S盒对密钥的敏感性。

3.1双射性

通常要求S盒是可逆的，尤其在代替置换网络中所使用的S盒必须是双射的。文献[4]给出了满足双射的充分必要条件：各分量布尔函数fi的线性运算之和为2n-1，即

(5)

式中，ai∈{0,1},(a1,a2,...,an)≠(0,0,...,0)；wt()表示汉明权重。如果式(5)成立，则f是平衡的，且是双射的。

本文中n=8，根据式(5)，满足双射性的标准值是128。该S盒的8个布尔向量共有255种线性组合形式。通过计算每种组合形式下向量异或值的汉明重量，可以发现结果均为28-1=128。因此该S盒满足双射性。

3.2非线性度

线性密码分析的目的是寻找密文、明文和密钥之间的有效线性表达式。S盒必须具有较高的非线性以抵御线性密码分析。

在实际运算时，通常将布尔函数f(x)转换成Walsh谱：

(6)

式中，ω∈GF(2n)；x·ω表示x和ω的点积，定义为x·ω=x1·ω1⊕...⊕xn·ωn。

则Walsh谱表示的非线性度为：

(7)

根据式(7)，S盒的非线性度输出为104、106、104、108、104、106、104和104。S盒和其他经典S盒[1,2,5,6]的非线性比较如表1所示。

表1　本文S盒非线性度与其他经典S盒比较

从表1中可以看出，S盒的非线性度平均值为105，优于其他几个经典的S盒生成方案。这说明该S盒能抵挡最佳线性逼近的进攻。

3.3严格雪崩准则(SAC)

为抵抗以输入的改变导致输出有相对较大改变为基础的攻击方法，Webster和Tavare首次提出严格雪崩准则。如果函数满足严格雪崩准则，则意味着一个输入比特的改变，将有一半的输出结果发生改变。

在实际运用中通过构造相关矩阵来验证布尔函数f是否满足SAC。在文献[7]给出相关矩阵的构造方法，对于相关矩阵A，如果其每个元素的值都接近0.5，则表明S满足SAC。

通过计算，得到该S盒的相关矩阵：

矩阵的均值为0.501 22，非常接近于理想值0.5。而Jakimoski的相关矩阵的平均值为0.497 2，Tang的相关矩阵的平均值为0.499 3，Chen的相关矩阵的平均值为0.499 9，Özkaynak的相关矩阵的平均值为0.504 8。进行对比，可发现该S盒的相关矩阵优于其余经典的S盒，说明该S盒能够很好地满足严格雪崩准则。

3.4输出比特间独立性(BIC)

文献[8]中指出，对于其中任意2个布尔函数fj,fk(j≠k)，如果fj⊕fk高度非线性且尽可能地满足严格雪崩准则，则可以保证当一个输入比特取反时，每个输出比特对的相关性接近于0。因此，可以通过验证S盒的任意2个输出异或fj⊕fk是否满足严格雪崩效应，来校验S盒的BIC特性。

通过计算，可得fj⊕fk(1≤j≤8,1≤k≤8)的非线性度矩阵：

其均值为103.643。而Jakimoski的BIC-非线性度的平均值为104.25，Tang的BIC-非线性度的平均值为102.96，Chen的BIC-非线性度的平均值为103.36，Özkaynak的BIC-非线性度的平均值为103.82。可以发现S盒在BIC-非线性度与经典的S盒不相上下。

计算输入序列中一个比特取反前后，输出序列y的任意2个比特异或值yj⊕yk变化的概率可得BIC-SAC：

BIC-SAC的均值为0.5000 7，非常接近理想值0.5。而Jakimoski的BIC-SAC的平均值为0.503 2，Tang的BIC-SAC的平均值为0.504 4，Chen的BIC-SAC的平均值为0.502 4，Özkaynak的BIC-SAC的平均值为0.500 7。对比发现，S盒的BIC-SAC平均值优于其他的经典S盒，说明该S盒具有较好的输出比特间独立性。

3.5差分均匀性

(8)

式中，α∈GF(2n)；β∈GF(2n)。

在实际计算中，也可以用差分逼近概率[10]来表示输入输出的异或分布状况：

(9)

式中，x∈GF(2n)。式(9)即表示给定输入差分为Δx，输出差分为Δy的最大可能性。

根据式(9)得到S盒的差分分布表，如表2所示。从表2中可以发现，输出差分的最大值为10。与经典S盒进行比较，Jakimoski的差分均匀度为10，Tang的差分均匀度为10，Chen的差分均匀度为12，Özkaynak的差分均匀度为10。由于差分表中的最大值越小，S盒的抗差分攻击能力越好。对比其他S盒的差分均匀度，可以发现该S盒与Tang和Özkaynak的方案同样具有很好的抗差分攻击能力。

表2本文S盒的输入输出差分分布表

3.6灵敏度分析

除上述5种准则外，动态S盒还需要具有对初始密钥有较高敏感性的特性。对于上述的128 bit密钥K改变最低位，得到新的初值K1，此时初值为x0=9C2B2E74D242D8279398B9719E5AF042，产生新的S盒。下面给出了与本文生成的S盒相应位置的部分数值：

通过比较这些相应数值可以看出，即使初始密钥的改变是微小的，所生成的S盒的变化很大。128 bit的密钥对应的密钥空间为2128，那么穷举攻击在理论上是不可行的。如果以子密钥作为动态S盒算法的初值，则随着每一轮子密钥的不同，将产生不同的S盒，更加增加了密码系统的加密强度。

4结束语

本文提出了依据系统密钥的动态S盒构造方法。该方法利用混沌映射的伪随机性，解决了S盒的固定结构问题，产生了对密钥敏感的动态S盒。而该算法主要的优点是通过改变系统的密钥可以产生许多不同的S盒，并且本文产生的动态S盒通过了评判标准。经过与经典S盒进行对比分析，发现该S盒具有最大的非线性度平均值，最接近0.5的SAC和BIC-SAC，最大值为10的输出差分。说明S盒可以有效地抵抗线性分析盒差分分析，具有优良的性能，适用于开发新的分组密码算法。

参考文献

[1]JAKIMOSKI G,KOCAREV L.Chaos and Cryptography:Block Encryption Ciphers Based on Chaotic Maps[J].Circuits & Systems I Fundamental Theory & Applications IEEE Transactions on,2001,48(2):163-169.

[2]ÖZKAYNAK F,ÖZER A B.A Method for Designing Strong Sboxes Based on Chaotic Lorenz System[J].Physis Letters A,2010(374):3 733-3 738.

[3]宋春艳.基于混沌理论的信息加密技术研究[D].哈尔滨：哈尔滨工程大学，2013.

[4]ADAM C,TAVARES S.The Structured Design of Cryptographically Good S-boxes[J].JCryptol,1990,3(1):27-41.

[5]CHEN G,CHEN Y,LIAO X F.An Extended Method for Obtaining S-boxes Based on Three-dimentional Chaotic Baker Maps[J].Chaos,Solitons and Fractals,2007,31(3):571-579.

[6]TANG G P,LIAO X F,CHEN Y.A Novel Method for Designing S-boxes Based on Chaotic Maps[J].Chaos,Solitons& Fractals,2005(23):413-419.

[7]WEBSTER A F,TAVARES S E.On the Design of S-Boxes[C]∥Advances in Cryptology CRYPTO ’85 Proceedings.Springer Berlin Heidelberg,1986:523-534.

[8]刘强，方锦清，赵耿，等.基于FPGA技术的混沌加密系统研究[J].物理学报，2012，61(13)：130508-1-5.

[9]BIHAM E,SHAMIR A.Differential Cryptanalysis of DES-like Cryptosystems[J].Journal of Cryptology,1991,4(1):63-72.

[10]HALE J K,VERDYNLUNEL S M.Introduction to Functional Differential Equations[M].New York:Springer-Verlag,1993.

范明慧女，(1989—)，硕士。主要研究方向：数字通信、信道编码和密码学。

仰枫帆男，(1966—)，教授，博士生导师。主要研究方向：信道编码理论和应用、信息论和协作通信等。

作者简介

收稿日期：2015-12-02

中图分类号TN918

文献标识码A

文章编号1003-3106(2016)03-0033-04