基于矩形独立覆盖初步实现结构静力分析的自动计算

苏海东,龚亚琦,颉志强,祁勇峰

（长江科学院材料与结构研究所,武汉 430010 )



基于矩形独立覆盖初步实现结构静力分析的自动计算

苏海东,龚亚琦,颉志强,祁勇峰

（长江科学院材料与结构研究所,武汉 430010 )

摘 要：采用前期研究的基于矩形独立覆盖的新型数值流形法,提出结构线弹性静力分析的自动计算方法,包括自动的前处理、自适应分析等。根据独立覆盖的特点提出几个后验误差指标:独立覆盖之间条形连接区域的应变连续性指标；边界应力指标和独立覆盖的高阶误差指标。利用新方法的h型网格加密及p型升阶的方便性,选择一种路径尝试h-p型的混合自适应,其中,对于矩形独立覆盖采用简单的二分法实现覆盖加密。通过几个二维算例验证了新方法实现自动计算的可行性,只需人工输入结构外形、材料参数和边界条件,其它工作完全交由计算机完成,最终得到满足一定精度的计算结果。

关键词：数值流形方法；独立覆盖；自动计算；误差估计；h-p混合自适应；静力分析

2016,33（02):144-150

1 研究背景

计算机辅助工程（Computer Aided Engineering, CAE),主要是指用计算机辅助求解复杂工程和产品的结构强度、刚度、动力响应、弹塑性等力学性能的分析计算［1］。提高分析效率对CAE意义重大,未来的发展趋势是让计算机自动、高效地完成分析,即CAE分析技术的自动化。

本文提出自动计算的思想,其目标是基本做到无需人工参与就能获得理想结果的分析,当然,必要的结构外形、材料参数和边界条件的人工输入除外。要达到此目标,必须解决CAE前处理的自动化、计算收敛效率及自适应等问题。其中,自适应是指在分析过程中由程序根据计算精度要求自动地提高数值计算中的近似函数的逼近程度,包括h型（加密网格)和p型（提高局部近似函数阶次)以及两者的混合方式［2］。目前来看,即使对于最基本的结构线弹性静力分析而言,以有限元法为代表的各种数值方法离自动计算的目标仍有不小距离。

有限元法在CAE中应用最为广泛,但其前处理的网格划分经常会耗费大量的人工工作量（据统计,前处理在计算分析总时间中所占比例往往高达80%以上［1］)。其原因在于,有限元网格不仅要模拟结构外形,还要保持合适的网格形状,以及网格之间通过结点的正确连接,而实际工程结构的复杂性使得网格剖分的难度较大。同时,由于求解域内物理场分布的复杂程度不同,需要网格密度的变化,比如目前广泛使用的h型自适应需要对精度不佳的区域进行网格细分,涉及到的大小网格过渡通常不太方便,要保持网格合适形状较为不易。在计算收敛效率方面,对于存在强奇异性的裂纹尖端（以下简称裂尖)等复杂应力场分布区域,用常规的有限单元插值函数逼近往往效果不佳。

广义有限元在结点上引入级数提高近似函数逼近能力,但其主要问题是高阶近似函数情况下的方程组线性相关［3-4］。扩展有限元在单元结点上增加附加函数:加入阶跃函数模拟裂纹两边的间断,可使裂纹横穿网格,同时在裂尖引入渐近位移场函数更好地模拟奇异性［5-6］。上述2种方法一般推荐采用均匀布置的规则有限元网格对求解域进行覆盖,但均匀网格在计算量上通常不经济,而不均匀网格的布置就仍存在大小网格的过渡问题。

无网格法直接借助离散点可构造出高阶连续的整体近似函数,在很大程度上克服了有限元法网格剖分的困难［7-8］。但其主要问题是:没有了网格,近似函数的构造要比有限元法难度大,计算成本较高,且在积分上一般需要特殊处理［8］。

综上所述,有限元法存在网格剖分困难、裂尖奇异区收敛慢等不足,无网格法存在实现相对复杂和计算量大等缺点,广义有限元存在的线性相关等问题,成为制约其实现自动计算的瓶颈。因此,笔者提出基于独立覆盖的新型数值流形方法,尝试结构静力分析及其自动计算的新途径。

2 新型数值流形方法

1991年,石根华博士［9］首次将现代数学“流形”思想引入工程计算,发明了数值流形方法（以下简称流形法),其中很关键的一点是:与有限元法将求解域离散成网格的方式不同,流形法构造物理场近似解的所谓“数学网格”与实际求解域分离（后者只用于定义积分区域),要求数学网格在空间上完全覆盖求解域。如图1（a)所示,图中着色的椭圆形物理区域被矩形数学网格完全覆盖。

对应于数学流形中的“覆盖”,数学网格又被称为数学覆盖。数值计算中,在各覆盖上定义覆盖函数作为局部近似函数Vi,通过单位分解函数φi联系

n起来形成整体近似函数V＝∑＝

φiVi（n为覆盖

i1 数)［9-10］。局部近似函数Vi一般为多项式级数,当然也可以是其它的完备级数,甚至是解析解级数。

到目前为止,流形法的数学网格一般是有限元网格［11］,并且推荐采用均匀的规则网格布置,在有限元结点上定义级数作为局部近似函数,单位分解函数就是有限单元的形函数。笔者称这种采用有限元数学网格的流形法为“常规流形法”,该方法实际上与广义有限元非常相似,也存在高阶函数情况下的方程组线性相关等问题。

从覆盖形式上看,有限元网格是一种完全重叠的覆盖,各覆盖没有自己的独立区域。2012年以来,笔者首次提出了部分重叠覆盖的“新型流形法”［12-13］,引入了“独立覆盖”,即单位分解函数φi＝1、近似函数就是给定级数Vi的覆盖区域。

首先研究了部分重叠的矩形覆盖。如图1（a)所示,标识为a—p的大网格即矩形的独立覆盖,覆盖之间只有较小的条形重叠区域。以图1（b)、图1 （c)中局部4个覆盖为例,每个覆盖包含1个独立区域和几个重叠区域,图中的大矩形为独立区域（即独立覆盖),P1—P4为相邻2个覆盖之间的重叠区域,P5为4个覆盖共同的重叠区域。建议条形厚度取较小尺寸,其单位分解函数φi取有限元的形函数实现覆盖之间的线性过渡［12,14］。独立覆盖还可以扩展到任意形状［15］。

笔者在文献［14］中进一步明确了新型流形法是基于独立覆盖的分析,并指出,独立覆盖具有任意形状、任意连接及任意加密的优良特性,突破了有限元网格的种种限制。如图2所示,只需对独立覆盖进行简单的再分块就可以方便地实现覆盖加密［13,16］,因此在h型自适应上具有很大优势,便于有针对性地加密覆盖及进行大小覆盖的连接过渡,从而提高求解效率。新方法在独立覆盖上直接给出某一阶的完备级数（如完全多项式),因此p型升阶也很方便。

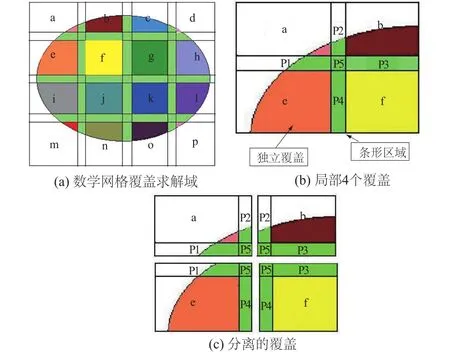
图1 部分重叠的矩形数学覆盖Fig.1 Schematic diagrams of rectangular mathematical covers with partially overlapping

图2 矩形独立覆盖的加密Fig.2 Refinement of a rectangular independent cover

新型流形法的部分重叠覆盖形式不仅解决了广义有限元和常规流形法在高阶情况下的线性相关问题［17］,而且还能在局部区域采用特殊覆盖函数以适合物理场局部特征。以裂缝分析为例,与扩展有限元在裂尖处的单元结点上增加渐近位移场的部分特征函数相比,新型流形法采用Williams解析解级数的独立覆盖函数是对裂尖位移场的最佳逼近,因此收敛更快［13,18］。另外,如果刚度矩阵采用数值积分方式,那么在计算公式及其程序实现上并不比有限元法复杂多少［12,18］,同样的带状稀疏正定矩阵适用于大型计算且计算量可控。

考虑到真实场函数的分布未知,靠人工布置覆盖及设定级数阶次以获得满意的计算结果仍然是不太容易。因此采用自动的前处理技术并结合有效的误差估计进行自适应分析是非常必要的,这就是自动计算的主要内容。相比其它方法而言,正是由于新型流形法具有的诸多优势,才使得在结构静力分析中尽早地实现自动计算成为可能。

3 误差估计初步研究

对当前计算结果进行精度分析的所谓“后验”误差估计主要有2种方法［19］:计算局部区域平衡方程残值的残值法；基于数值解的后处理结果的误差估计,如O.C.Zienkiewicz和J.Z.Zhu提出的ZZ法。前者数学理论基础比较完善,但由于形式复杂而没有得到广泛应用；后者具有计算简单、易于理解的优点,受到工程界的广泛欢迎。本文以后者为主。

设ε为精确应变（对于常量弹性矩阵D,研究应力或应变效果相同),ε＾为数值计算得出的应变,则差值为

能量范数误差定义为［19］

精确的能量为［19］

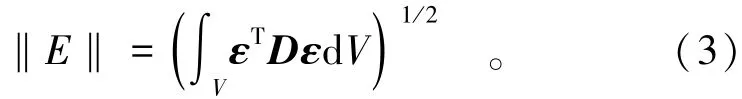
真实应变ε通常是未知的,改用一个相对准确值ε*代替,则‖E‖和‖ΔE‖分别成为‖E*‖和‖ΔE*‖。定义误差估计的有效性指数［19］为

其值趋向于1表明有渐近精确性。

相对误差定义为［19］

关于相对准确值ε*,本文研究了以下几种误差指标。

3.1 条形处的应变连续性指标η1

有限元中的ZZ法对相邻单元结点的应力平均,或对多个单元组成的单元片进行最小二乘的应力平滑,作为相对准确解。前者方法简单但精度不高,后者的精度随单元片增大而提高,但计算量上升。

新型流形法在覆盖的独立区域已具备高阶光滑的应变,只是在覆盖的条形重叠区域容易发生应变的突变,是误差最大的地方。受ZZ法的启发,本文以条形区域的应变为突破口:当2个覆盖在其条形重叠区域的应变相差不大时,表明在这2个覆盖区域的应力基本连续平滑；当更多的覆盖达到此要求后,将使成片区域以至于整个求解域的应力平滑,这样就可以避免采用最小二乘法进行应力平滑的较大计算量。

图3 两个相邻覆盖及其条形区域的应变Fig.3 Strains of two adjacent covers and strip area

以一维问题的2个覆盖为例,假设应变分布如图3所示。图中左、右两边的黑色曲线分别表示覆盖1和覆盖2的应变曲线ε1和ε2,灰线为

研究实例表明,随着覆盖函数阶次的提高和覆盖尺寸的减小,ε1和ε2两条应变曲线在条形连接处逐渐接近,因此将其接近程度作为应变连续甚至平滑的判据是很直观的想法。可将红线作为相对准确的应变ε*,即Δε＝ε*-ε1或Δε＝ε*-ε2,两者相同,然后按式（5)计算η1。

3.2 独立覆盖内的自由表面应力指标η2

在具有自由表面的独立覆盖内,计算

3.3 独立覆盖内的高阶误差指标η3

参考文献［20］,以一维为例,精确解u按近似解的级数uh展开到m阶,即

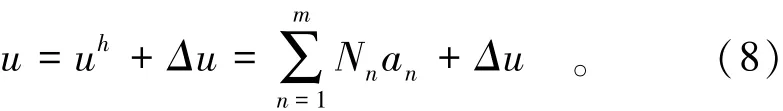
式中: Nn和an分别为级数的单个函数及其系数,两者的差值假设为级数的第m＋1阶函数,即

应变误差为

则一般情况下的二维和三维能量范数误差

假定当Nm＋1am＋1加入到近似解时,原来参数a1,…,am保持不变。设RV为取到m项时将uh代入到微分方程后的残值,再次应用伽辽金法逼近am＋1,得到

将式（12)代入式（11)得到

然后按式（5)计算η3,其中ε*按当前近似解uh计算。

该指标表明了采用高阶后对计算结果的改进,但其主要问题是［20］:Nm＋1可能与积分域内的残差RV正交,得到误差估计为0；假定a1,…,am保持不变,且新解与原来解之间的任何相互影响都忽略不计,而这些条件在实际计算中很难完全达到。文献［20］用一维算例说明,这种方式得到的‖ΔE‖是误差能量模的上限。

4 自动计算初步研究

新型流形法的前处理包含2个步骤,其一是形成如图1所示的矩形数学网格；其二是切割操作,即数学网格与物理边界相互切割,生成网格内的物理积分区域（又称为流形单元)。需要强调的是,切割只涉及简单几何运算［21］,可完全自动化,规则的矩形数学网格（含独立覆盖及其条形连接)的生成也很简单,因此前处理难度大大降低。目前,上述过程已编写了计算机程序,只需人工输入结构的轮廓,就能自动完成网格生成和切割操作,再结合人工输入的材料参数和边界条件,自动生成计算数据,实现完全自动化的前处理。

新型流形法具有h型覆盖加密和p型覆盖函数升阶的双重便利性,理论上可通过h型和p型的适当组合达到最高的计算收敛效率,这就是h-p型自适应的最佳路径。本文暂不考虑计算效率问题,而是选择一种路径尝试h-p型的混合自适应,其计算步骤为:

（1)在初始的矩形覆盖网格上,首先进行独立覆盖函数的p型升阶——对于多项式级数,从2阶开始,最高升至4阶；对于裂尖Williams解析级数, 从3阶开始,最高升至5阶。

（2)如果精度不满足,再进行h型覆盖加密,对于本文研究的矩形覆盖,暂时采用最简单的二分法,如图4所示,将图4（a)的一个独立覆盖沿x向和y向分别均分为二,一共划分为图4（b)的4个小覆盖。然后,重新进行前处理。

（3)再回复到步骤（1)进行p型升阶,目前仍从最低阶开始计算。

循环往复直至所有区域达到设定的误差指标。但对于凹角、裂尖等具有奇异性的区域,网格越加密,应力越大,不可能达到预设精度,因此设定网格加密的最多次数适时停止计算。

覆盖加密和升阶判断中的误差指标是第3节中定义的η1,η2和η3,对于η1超标时涉及的2个覆盖都进行升阶或加密操作,如图4（b)所示,当右边水平向条形的误差超标时,加密成图4（c)的形式。

以上自适应过程由计算机自动完成。再加上自动化的前处理,就能初步实现自动计算。

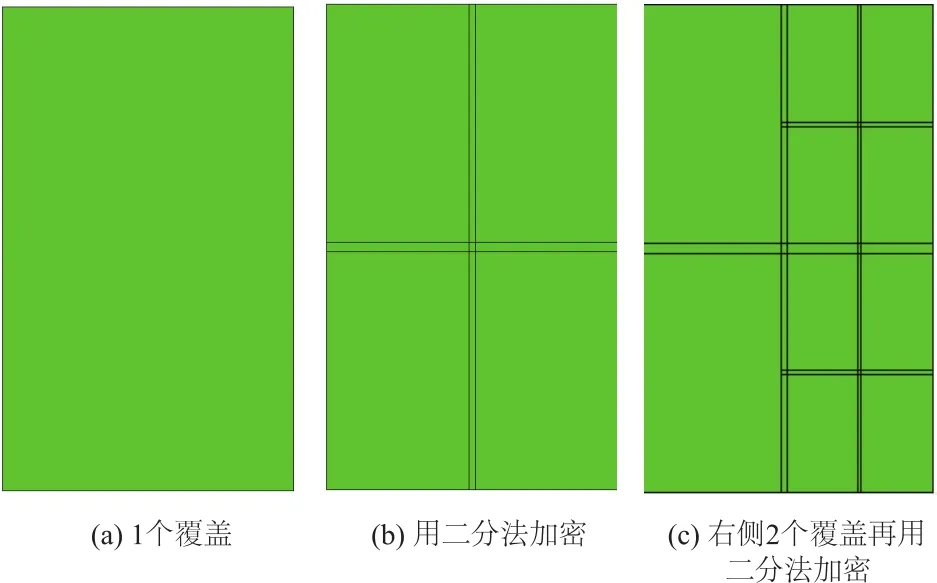
图4 矩形覆盖加密的二分法Fig.4 Bisection method for refinement of rectangular covers

5 结构静力分析的自动计算算例

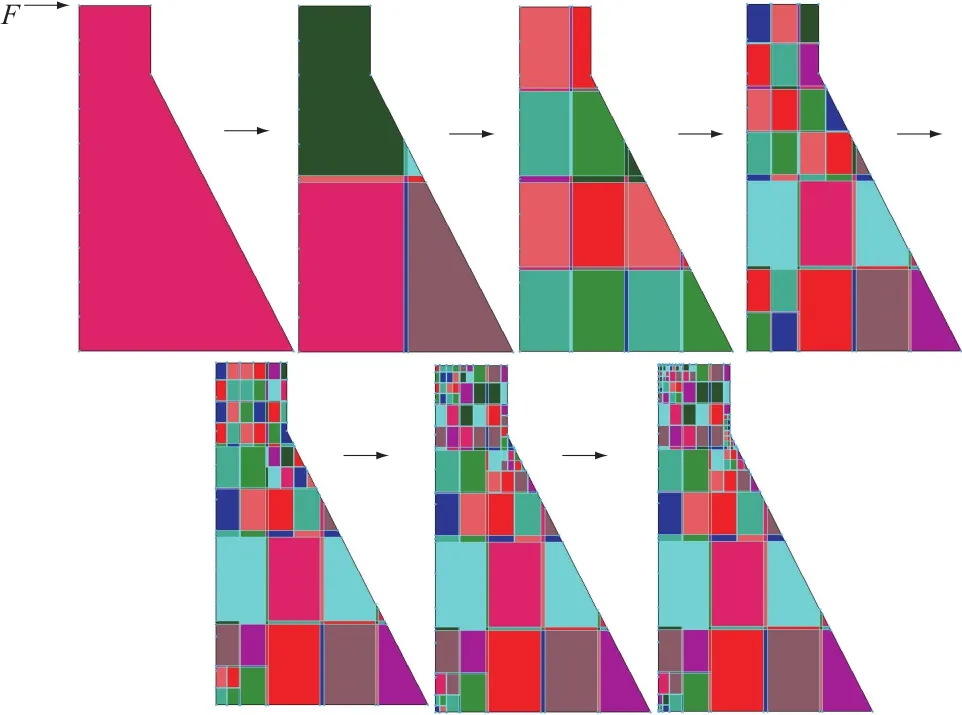
图5 重力坝的覆盖自动加密过程Fig.5 Procedures of automatically refining covers in a gravity dam model

5.1 算例1——上游表面顶点受集中力作用的重力坝

如图5所示的重力坝,坝高100 m,坝底长60 m,坝顶宽度20 m,下游面折角处距坝顶20 m。坝体弹性模量为30 GPa,泊松比为0.167。上游表面顶点受集中力作用F＝1 000 kN。采用积分形式的罚函数法（即硬弹簧)实现底部的全约束。另采用稠密网格的有限元计算结果作为参考解。预设误差指标为:η1＝0.05,η2＝0.15,η3＝0.05。

不妨从1个覆盖开始计算。程序在误差指标的控制下自动地进行覆盖函数升阶及覆盖加密,如图5所示,加密的覆盖逐渐趋向于集中力作用点、坝踵及下游坝面拐点等应力奇异部位。最终得到的上游面应力见图6,图6（a)的垂直应力与细密网格的有限元参考解吻合很好,相对误差均在2%以下, 图6（b)的自由面应力大都在0.001 MPa以下,与理论应力值为0非常接近。

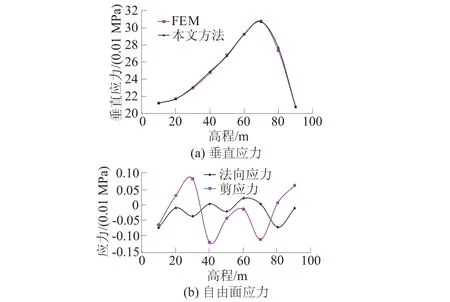
图6 重力坝上游面应力Fig.6 Stresses on the upstream surface of the gravity dam

5.2 算例2——方孔

中部开小方孔的矩形板在上、下两端受均布拉力p＝10 kN/ m2,采用如图7所示的1/4计算模型,左边和底部用积分形式的罚函数法施加法向约束。同样从1个覆盖开始计算（当然也可以事先自动划分较多的覆盖)。从表1可见,经过5次自动加密后,孔口测量点的应力值与有限元细密网格参考解的误差在3%以下。加密的覆盖也是逐渐趋向于孔口的角点奇异部位,而在应力变化平缓的区域则是自动地采用大覆盖和较低的多项式阶次（2阶居多),在计算量上体现出经济性。

图7 方孔的1/4计算模型Fig.7 1/4 model of a rectangular plate with a small internal square hole

5.3 算例3——I型裂缝的应力强度因子

图8 两端受均布拉力的长条平板示意图(含边界裂纹)Fig.8 A long plate with a boundary crack subjected to a uniform tension

如图8所示的无限长条平板两端受均布拉力P＝3 kN/ m,平板宽w＝0.4 m,含边界裂纹长a＝0.05 m。应力强度因子KI的理论值1.45 kPa/ m1/ 2［22］。

如图9所示,经过图9（a)至图9（e)的几次自动加密后,裂尖应力强度因子KI计算值分别为1.67, 1.40,1.52,1.46,1.47,最后与理论值1.45很接近。

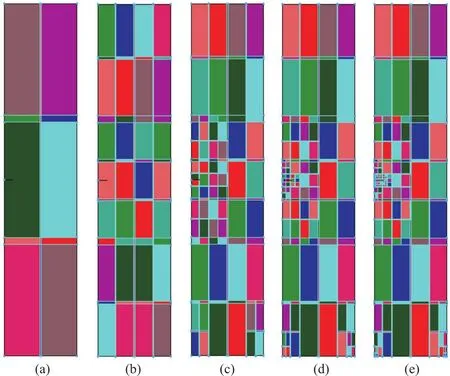
图9 计算应力强度因子的流形元网格Fig.9 NMM meshes for calculated stress intensity factor

表1 孔口测量点切向应力比较Table 1 Tangential stresses of the measuring points at the orifice　0.01 MPa

本例的特点是在裂尖所在的局部覆盖中采用了Williams解析级数作为覆盖函数,即图10中的裂尖解析覆盖,因此收敛很快,计算精度高,而且应力强度因子作为级数的系数直接得到。

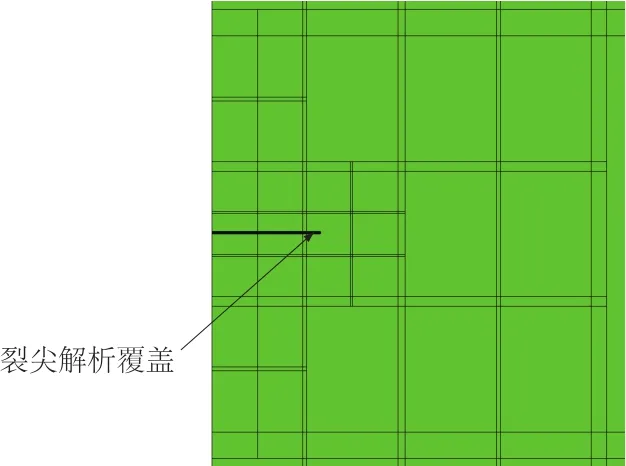
图10 图9(d)中的裂尖附近局部网格Fig.10 Local NMM meshes around the crack tip in Fig.9(d)

此例加密覆盖时,为避免条形区域落到裂尖附近,对裂尖所在的覆盖在y方向采用了三等份。但实际操作中不容易使裂尖位于独立覆盖的中心。如图9（c)所示,当裂尖靠近独立覆盖的边缘时,计算精度会下降。

另一个发现是,裂尖附近并非越加密越好。这是因为,越靠近裂尖,位移场和应力场的变化梯度越大,与解析覆盖相连的数值覆盖就要求达到更高的阶次。因此,对于裂尖等奇异区,如何合理地划分覆盖及设定覆盖函数阶次的问题需要进一步研究。

6 结 语

本文采用基于矩形独立覆盖的新型流形法,初步实现了二维结构线弹性静力分析的自动计算:只需人工输入结构外形、材料参数和边界条件,其它过程完全交由计算机自动完成,最终能得到满足一定精度的计算结果。但限于研究时间较短,在h-p自适应路径及计算效率上没有优化,因此只是自动计算的初步研究。考虑到计算效率是关系到新方法是否具有实际应用价值的重要问题,下一步将从以下几方面加以改进。

（1)将矩形覆盖扩展到任意形状覆盖。本文基于矩形覆盖进行的自动计算,可以直接推广到三维长方体覆盖。但对于复杂求解域,矩形覆盖很可能造成边界附近各覆盖内的材料体大小不均,位移和应力的复杂程度分布不均,使自适应分析效率下降。因此,针对求解域形状进行覆盖划分是有必要的,这就要将矩形覆盖扩展到任意形状覆盖,使覆盖贴合结构外形并能模拟不同材料分区,同时也能做到准确施加本质边界条件。

（2)研究覆盖的合理布置。考虑到新型流形法的灵活性,总会有相对合适的覆盖形状、大小以及连接方式可使计算效率大幅提升。从本文几个算例可知,裂尖、孔口角点等处具有应力分布的奇异性,自适应分析后期的很多过程都围绕它们进行。如果能够根据物理场的先验知识,研究出合理的覆盖及函数形式在这些局部区域预先布置,就可以减少自适应分析的步骤,大大提高计算效率。

（3)研究h-p自适应的最佳路径和提高计算速度的算法。新型流形法的计算量可控,理论上可以通过h-p自适应的最佳路径达到最小的计算量。同时,自适应分析需要反复计算,如何利用前次计算结果以加快当前计算速度还有待研究。因此,新方法的自动计算还有很大的效率提升空间。

（4)误差估计理论有待进一步完善。目前的误差指标与真实误差的差别有多大（需要研究各指标的有效性指数)？是否对所有情况都有效？如果只关注局部区域的精度,如何确定局部误差？这些问题还有待解决。

最后需要指出,本文提出的自动计算思想不仅是上述的自动前处理和h-p型混合自适应,而且是贯穿整个计算过程的自动化:采用可具有任意形状、任意连接、任意加密的覆盖网格,基于CAD精确几何描述进行自动化的前处理；针对求解域形状特征、根据物理场先验知识进行自动化的覆盖布置和覆盖函数选取；通过最佳的h-p型混合路径进行高效的自适应重复计算；最后基于高精度应力结果进行自动化的后处理。最终目标是结构分析自动化CAE软件。

致谢：部分重叠覆盖的思想来自于石根华博士。笔者的研究一直受到石根华博士的指导，在此表示由衷的感谢。

［1］ 百度百科.CAE［EB/ OL］.（2015-06-11)［2015-07-10］. http:∥baike.baidu.com/ view/112169.htm.

［2］ ZIENKIEWICZ O C, TAYLOR R L. The Finite Element Method（The Fifth Edition)［M］. Oxford, Great Britain: Butterworth-Heinemann, 2000.

［3］ DUARTE C A, BABUSKA I, ODEN J T. Generalized Finite Element Methods for Three-dimensional Structural Mechanics Problems［J］. Computer＆Structures, 2000, 77:215-232.

［4］ 李录贤,刘书静,张慧华,等.广义有限元方法研究进展［J］.应用力学学报, 2009, 26（1): 96-108.

［5］ MOES N, DOLBOW J, BELYTSCHKO T. A Finite Element Method for Crack Growth without Remeshing［J］. International Journal for Numerical Methods in Engineering, 1999, 46: 131-150.

［6］ 李录贤,王铁军.扩展有限元法（XFEM)及其应用［J］.力学进展, 2005, 35（1): 5-20.

［7］ BELYTSCHKO T, KRONGAUZ Y, ORGAN D, et al, Meshless Methods: An Overview and Recent Developments［J］. Computer Methods in Applied Mechanics and Engineering , 1996, 139: 3-47.

［8］ 张 雄,刘 岩,马 上.无网格法的理论及应用［J］.力学进展, 2009, 39（1): 1-36.

［9］ SHI G H. Manifold Method of Material Analysis［C］∥U. S. Army Research Office. Transactions of the Ninth Army Conference on Applied Mathematics and Computing. Minneapolis, Minnesota, U S A, June 18-21,1991:57-76.

［10］BABUSKA I,MELENK J M.The Partition of Unity Method ［J］. International Journal for Numerical Methods in Engineering,1997, 40:727-758.

［11］张湘伟,章争荣,吕文阁,等.数值流形方法研究及应用进展［J］.力学进展, 2010, 40（1): 1-12.

［12］祁勇峰,苏海东,崔建华.部分重叠覆盖的数值流形方法初步研究［J］.长江科学院院报, 2013, 30（1): 65-70.

［13］SU Hai-dong, QI Yong-feng, GONG Ya-qi, et al. Preliminary Research of Numerical Manifold Method Based on Partly Overlapping Rectangular Covers［C］∥DDA Commission of International Society for Rock Mechanics. Proceedings of the 11th International Conference on Analysis of Discontinuous Deformation（ICADD11).Fukuoka, Japan, August 27-29, 2013: 341-347.

［14］苏海东,颉志强,龚亚琦,等.基于独立覆盖的流形法的收敛性及覆盖网格特性［J］.长江科学院院报, 2016,（2):131-136.

［15］苏海东,祁勇峰,龚亚琦,等.任意形状覆盖的数值流形方法初步研究［J］.长江科学院院报,2013,30（12): 91-96.

［16］苏海东,祁勇峰.部分重叠覆盖流形法的覆盖加密方法［J］.长江科学院院报, 2013, 30（7): 95-100.

［17］林绍忠,苏海东.数值流形法独立覆盖区域的一种自动选取方法［J］.长江科学院院报,2014,31（12):88-91.

［18］苏海东,祁勇峰,龚亚琦.裂纹尖端解析解与周边数值解联合求解应力强度因子［J］.长江科学院院报, 2013, 30（6): 83-89 .

［19］AKIN J E.Finite Element Analysis with Error Estimators ［M］. Oxford, Great Britain: Elseviewer Butterworth -Heinemann,2005.

［20］O C辛克维奇,K摩根.有限元与近似法［M］.陶振宗,张述良,周之德,译.北京:人民交通出版社,1989.

［21］石根华.数值流形方法与非连续变形分析［M］.裴觉民译.北京:清华大学出版社, 1997 .

［22］中国航空研究院.应力强度因子手册［M］.北京:科学出版社,1993.

（编辑:刘运飞)

Preliminary Implementation of Automatic Computation for Static Analysis of Structures Using NMM Based on Independent Rectangular Covers

SU Hai-dong, GONG Ya-qi, XIE Zhi-qiang, QI Yong-feng
（Material and Engineering Structure Department,Yangtze River Scientific Research Institute, Wuhan 430010,China)

Abstract:By means of numerical manifold method（NMM) based on independent rectangular covers proposed in previous study, we present an automatic computation method for static analysis of linear-elastic structures, including automatic pre-processing, self-adaptive analyses and so on. According to the characteristics of independent covers, we give 3 indexes for posterior error such as index of strain continuity in strip area between two covers, stress index on boundary surfaces and high-order error in an independent cover. By using convenient h-version mesh refinement and p-version order increasing in the new method, we implement h-p version self-adaptivity in a selected way to realize h-version refinement of rectangular covers by using simple bisection method. Some 2D numerical examples are given to illustrate the feasibility of automatic computation, in which all the procedures are automatically accomplished by the computer, except for necessary manual input of structural outlines, material parameters, and boundary conditions. Finally, we obtain calculated data with certain precision.

Key words:numerical manifold method（NMM)；independent covers；automatic computation；error estimation；h-p hybrid adaptivity；static analysis of structures

作者简介：苏海东（1968-),男,湖北武汉人,教授级高级工程师,博士,主要从事水工结构数值分析工作和计算方法研究,（电话)027-82927167（电子信箱)suhd@ mail.crsri.cn。

基金项目：国家自然科学基金项目（51409012)；中央级公益性科研院所基本科研业务费项目（CKSF2013031/ CL,CKSF2014054/ CL)

收稿日期：2015-10-30;修回日期：2015-11-25

doi:10.11988/ ckyyb.20150919

中图分类号：TB115;TV311

文献标志码：A

文章编号：1001-5485(2016)02-0144-07