面向大规模图数据的并行图布局算法

2016-04-08程致远鲍玉斌冷芳玲

大数据 2016年5期

关键词：引力复杂度顶点

程致远，鲍玉斌，冷芳玲

东北大学计算机科学系，辽宁沈阳 110819

面向大规模图数据的并行图布局算法

程致远，鲍玉斌，冷芳玲

东北大学计算机科学系，辽宁沈阳 110819

图模型是一种广泛使用的建模工具。图的可视化作为一种直观的图数据分析工具被广泛使用。图数据可视化中最关键的技术是图布局算法，但是目前并没有高效的并行图布局算法，因此目前对于海量图数据的可视化是一个挑战性问题。针对这一问题，在力导向布局算法基础上，忽略弱关联顶点间的斥力计算，提出了k-friend布局算法；并针对海量图数据设计了高效的并行图布局算法。在人工和实际数据集上的测试结果表明，在布局质量降低可容忍的情况下，该算法大幅度提升了布局的速度。

力导向算法；可视化分析；社交网络；并行布局算法

1 引言

图模型是一种广泛使用的建模工具，许多应用问题都可以抽象成图，如社交网络就可以用图模型进行表示。图数据的可视化技术可以将图的邻接表或者邻接矩阵转换为直观的、用点和线组成的图形，可以令研究人员直观地看到图数据的关联关系和结构，是图数据分析的一种非常常用并且重要的手段。图可视化技术中关键的一个环节是图的布局算法。

力导向布局算法是目前最为常用的图布局算法，其优点是可以清晰地展现出图的社区结构，并且也能很好地展现出顶点之间的关联关系，是由Peter Eades提出的。该算法通过模拟物理学的概念，认为图中的每一个点都受到引力和斥力的影响，邻居顶点之间互相有吸引力，所有顶点之间存在排斥力，如果两个顶点之间的吸引力大于排斥力，则这两个顶点会被调整到更近的位置；反之，如果两个顶点之间的排斥力大于吸引力，则这两个顶点会被调整到较远的位置。其意义是可以使得关系紧密的顶点最终被放置到相对靠近的位置，不相关的顶点会被放置到相对较远的位置。从而，用户可以根据两个顶点间的距离得知这两个顶点的相关性的强弱，同时，排斥力还可以使顶点之间存在一定的距离，使得网络中的顶点不会因为太密集或者重叠而影响视觉观察效果。

但是目前力导向算法的时间复杂度大多都是O(n2)，难以对大规模图数据进行布局，并且由于图数据的特点是顶点之间的关系错综复杂，其中任何一个顶点位置的改变都会影响其他所有顶点的位置，因此很难进行并行化。

以上原因使得目前的图布局算法不能适用于顶点数和边数很大的图。面对目前数据量越来越大的社交网络数据，亟待一个能够对大规模图数据进行布局的布局算法。本文通过忽略部分弱关联顶点的斥力计算，在牺牲少量布局质量的情况下，大幅度提升布局的速度，并且在此基础上提出了并行计算的算法，最后测试表明，本文提出的图布局算法在图顶点数较多时，在计算速度上有比较大的提升，并且布局质量下降的并不明显。

2 相关工作

通常应用问题建模得到的图结构（如社交网络结构、Web连接图结构等）都是拓扑图。拓扑图可视化技术的核心是图布局算法。关于图布局算法已经有许多的研究，同时也提出了一些图可视化布局算法。目前图布局算法主要分为3种：力导向布局算法、限定图的展现形式和利用数据自身属性信息的布局方法。

力导向布局算法[1]的主要思想是将整个拓扑图看作一个物理系统，相邻顶点之间存在引力，不相邻的顶点间存在斥力，每次迭代计算顶点受到的合力，并根据合力移动顶点，最终使整个系统达到一个能量的极小值。该布局算法对目前的社交数据有很好的展现效果，可以清晰地表现出顶点间的邻接关系以及整个图的社区结构。代表性的算法有Fruchterman等人的FR算法[2]、Hu Y F提出的Hu氏算法[3]、Hadany等人提出的HH算法[4]、Kamada等人提出的KK算法[5]、GGK算法[6]等。力导向布局算法最早是由Eades在1984年提出的，基本思想是将整个图看作一个顶点为钢圈、边为弹簧的物理系统，每个顶点被赋予初始位置后会根据受到的斥力和引力调整位置，直到整个系统达到一个稳定的状态。之后很多研究者针对Eades的算法提出了一些改进算法，如KK算法、FR算法。HH算法首次使用了分层布局的手段，先返回一个粗略的结果，再绘制细节。这些算法的每一步迭代的时间复杂度都为O(n2)。Hu氏算法将远距离的一簇顶点聚集为一个超点，将每次迭代的时间复杂度降低到O(nlgn)。2014年Jacomy M针对FR算法提出了很多工程上的改进，提出了局部速度的概念，使得每个顶点每次迭代可以移动的最大位移与其出度成正比，加快了算法收敛的速度，但其本质仍是FR算法，时间复杂度为O(n2)。力导向布局算法布局效果如图1所示，本文提出的算法也是基于力导向算法的思想，但是由于这种算法的时间复杂度较高，一般不适合做大规模图数据的展现，因此本文对这种算法进行了改进：对图中顶点间的斥力的计算进行了近似处理，认为不（直接）相关联的顶点之间的斥力可以近似计算，以提高算法的计算效率。

限定图的展现形式的思想是对图进行布局之前，预先设定好图的展现形式，每一个顶点在布局时都直接放在预先设定好的位置上，不需要考虑图的整体拓扑结构，从而可以快速地对海量数据进行布局。该算法的时间复杂度为O(n)。但是这种布局算法并不能反映出顶点之间的关联关系，所以，一般不会用于对需要反映图数据的整体结构的数据进行布局。这类算法的代表有圆形布局法[7]和矩形布局法[8]等。

图1 力导向图示例

目前很多图数据都会附带地理位置等信息，因此在这类图数据进行布局时可以利用数据自身的位置属性信息。利用数据自身属性信息的布局方法就是充分利用图数据自身的这部分信息进行布局，如地图布局[9]等。这类算法的时间复杂度为O(n)，但是并不是所有的图数据都有可以利用的属性信息，因此不能用于没有位置信息的图数据的布局。

以上布局方法中，只有限定图的展现形式和利用属性信息的算法可以对大规模图数据进行布局，但是它们具有局限性。力导向类算法由于时间复杂度太大，不适合对大规模图数据进行布局。因此，这方面的研究比较少，Tikhonova A提出了一种FR算法的并行实现策略[10]，实验表明该算法随着处理器核心数量的提高，算法的计算时间线性减少，但是作者并没有测试这种算法在大数据下的性能，因为FR算法每次迭代的时间复杂度为O(n2)，所以在数据量变大时该算法的性能不会很好。

力导向算法在处理社交数据时有很大的优势，可以清晰地显示图社交数据的社区结构和关联关系。因此，目前对于社交数据的布局大都使用力导向布局算法。力导向布局算法又称为“弹簧算法”，目前最广泛使用的是FR算法。

FR算法定义直接相连的顶点间存在引力，不直接相连的顶点间存在斥力，每一次迭代，分为3步：第一，对每个点计算其与相邻顶点之间的引力；第二，对每个点计算其与其他所有顶点之间的斥力；第三，对每个顶点根据其引力和斥力的合力，调整其位置。调整位置的距离取决于一个退火函数。然后根据新得到的位置不断迭代上述的3步，直到达到指定的迭代次数，或者这个系统的能量小于一个阈值。所有的力导向布局算法基本都是基于这个框架。由于FR算法要计算任意不相邻顶点之间的斥力，所以导致算法每一次迭代的时间复杂度为O(n2)。

传统力导向布局算法之所以要对任意的两个顶点计算斥力是为了使不相关的顶点之间的距离尽可能的远。而通过观察发现，在对大规模图数据进行分析时，通常只关心关系比较紧密的顶点之间的位置关系，而对于关系不紧密，甚至无关的两个顶点，并不关心它们之间的距离是否跟它们之间关系的紧密程度成正比。换言之，人们只是希望这两个顶点的距离不要太近，至于它们之间的距离到底多远，对分析数据几乎没有影响。在这个前提下，可以通过只计算与一个顶点关系紧密的k个顶点（如它的第一跳和第二跳邻居）之间的引力和斥力的方法，将原本O(n2)时间复杂度的布局算法改进为时间复杂度为O(kn)的算法。k的值越大，计算越精确，同时性能也越低，当k为n-1（n为图的顶点数）时，本文算法就退化为FR算法，时间复杂度变为O(n2)。用户需要根据自己对于计算结果精确度的需要，设置k的大小。

3 近似力导向布局算法（k-friend布局算法）

传统的力导向算法认为任何顶点之间都存在斥力，这样可以使得不相干的顶点之间的距离较远，但这样也使得计算的时间复杂度达到了O(n2)。在处理大规模图数据时，人们往往只关心关联关系较大的顶点之间的位置关系，而不相关或者相关性很小的两个顶点之间的位置人们并不关心。换言之，人们希望看到关联相对紧密的顶点之间的距离与关联的紧密程度成正比，关联程度越紧密，它们的距离越近，而对于关联程度弱的顶点，它们之间的距离具体有多远，人们并不关心，只要不是太近就可以接受。因此对于联系不紧密的顶点，可以不计算他们之间的斥力，即在用传统力导向算法计算任意顶点间的斥力时，只计算关系最紧密的k个顶点之间的斥力，这样可以在很大程度上降低算法的时间复杂度。因此，本文称这种算法为k-friend布局算法。这里的k实际上是一个控制顶点数量的参数，它的确定应该与一个顶点的平均几跳邻居数有关，如果只考虑一跳邻居，则是只考虑与一个顶点直接相连的邻居数，如果考虑两跳邻居，则是一个顶点的两跳之内的所有邻居之和。当这个顶点数超过了k的限制，就要采取一些措施控制邻居的总数。这是因为，在真实图中，很可能会存在超级顶点，即这个顶点的邻居数远远大于其他顶点，这时从计算效率考虑，需要从中选择k个顶点。k-friend布局算法具体的实现原理如下。

先介绍算法需要的数据结构。每一个顶点包括顶点信息vertex和边信息edges，使用二元组表示为＜vertex,edges＞；顶点v信息中包含顶点ID、顶点属性、坐标信息和与该顶点关系最紧密的k个顶点的集合friendSet（friendSet=＜friend1,friend2…friendk＞），即vertex=＜vertexID,attr,coord, friendSet＞。其中，friendSet中每一个数据项friend包括顶点u的ID和与顶点v之间的深度deep（即顶点v与顶点u之间的连接跳数），即friendi=＜vertexID,deep＞；坐标信息中包括上一次迭代和本次迭代顶点的坐标，即coord=＜oldx,oldy,x,y＞。边的信息包括目的顶点I D和边的权值，即edges=＜(destVertexID1,weight1), (destVertexID2,weight2), …, (destVertexIDm, weightm)＞。

k-friend布局算法主要分为如下4个步骤。

步骤1 对图数据进行预处理，对每个顶点使用深度优先搜索找出其跳邻居，n表示顶点与其n阶以上的邻居之间的关系是可以被忽略的，n越大，布局越接近FR算法，同时计算时间也会变长，因此用户要根据自己对于精确度的需要来设置n的大小，如果数量大于k则在其中随机选取k个。将这k个顶点的顶点ID和深度保存在顶点的friendSet中。经过以上步骤后，会得到每个顶点的n跳邻居集合friendSet =＜(vertexI D1,deep1),(vertexID2,deep2)，…，(vertexIDk, deepk)＞。

步骤2 为每个顶点分配一个初始位置。位置的分配策略已经有很多的研究成果，本文采用与FR算法一样的随机分配策略。

步骤3 计算引力和斥力。对于每个顶点计算其与邻居节点之间的引力fa(u,v)。计算其与friendSet中的节点的斥力fr(u,v)。具体引力斥力计算式有很多选择，可以根据需要选择不同的引力计算式，本文采用的是fa=d2/k、fr=k2/d，k为用户认为顶点之间最理想的距离，不影响布局结果，调整k相当于对图进行整体缩放，d为两个顶点之间的距离。引力和斥力计算式的算法会影响布局结果的社区属性，可以通过调整引力和斥力的计算式使得布局结果更有社区结构，参考文献[11]进行了深入的研究和探讨。引力计算式的选择不影响布局算法的本质，只会对布局细节产生影响。

步骤4 根据顶点受到的斥力和引力调整顶点的位置。顶点移动的最大距离可以根据退火算法进行动态的调整。

步骤5 重复执行步骤3和步骤4，直到达到最大迭代步数，或者整个系统的能量小于给定的阈值。

该算法在布局阶段每一次迭代的时间复杂度可以达到O(kn)。k为每个顶点friendSet的大小，在预处理阶段由用户指定。

k-friend布局算法描述如下。

要注意的是本算法虽然提升了时间复杂度，但是增加了空间复杂度，需要O(kn)的额外空间用以存储顶点的friendSet。不过目前图布局算法的瓶颈在于计算速度方面，内存相对很宽裕，尤其是对于分布式计算系统而言。并且笔者认为如果要使算法高效地并行化，那么friendSet是必不可少的。值得注意的是k的值越大，计算越精确，同时性能也越低，当k为正无穷大时，本文算法等于FR算法，时间复杂度退化为O(n2)。用户需要根据自己对于计算结果精确度的需要设置k的大小。

4 分层策略

由于只计算了关系相对紧密的顶点之间的斥力，这可能会导致关联不紧密的顶点被布局到非常近的位置，虽然这样的概率很低，这种情况会通过分层布局的方式进一步降低这种情况的发生概率。

分层策略采用O DL（out degree layout）算法[12]，ODL算法是Chan提出的一种基于力导引算法的变种算法，并针对幂率分布的网络提出了分层算法，比较适合于社交网络。

ODL算法如下：首先对图节点按照出度分类，将节点划分到不同的层级L1…LM，然后从出度最大的一层开始布局，将顶点不断地加入上一层中，最终形成完整的布局结果。只要保证最初的第一级节点构成的图能够近似地反映图的整体结构，那么后面全部节点的调整过程将会大大缩短，同时也会使得不相关的顶点不被放置到相近的位置。这是因为不相关的顶点往往都会与不同的上层顶点有关系，所以会被放置在不同的上层顶点附近，而对于上层顶点可以采用精确的计算。因此，不同的上层顶点位置不会太近。ODL算法在计算第一层的时候会使用传统的力导向算法，后面各层的计算采用改进的力导向算法。ODL算法如下。

5 并行的近似计算力导向布局算法

虽然进行了上面提到的种种优化，但是面对目前数百万顶点的数据还是显得力不从心，因此笔者使用分布式并行计算的方法进一步提升算法的计算能力。关于大数据的并行计算模型有很多，如MapReduce模型和大块同步模型（BSP模型）。本文使用BSP编程模型进行编码。

主要过程如下。

步骤1 找到每个顶点的n阶邻居，并将其存储在顶点的friendSet中。

步骤2 将处理好的顶点数据分发到每一台机器中，每台机器会遍历顶点数据。对于每一个顶点，将其位置发送给其friendSet中的顶点。

步骤3 每一个顶点在收到其friendSet中的顶点给自己发送来的位置后，算出自己与这个顶点的距离，然后判断这个顶点是不是与自己有边的顶点，如果是，则计算引力和斥力；如果不是，则只计算斥力，然后根据引力和斥力的合力，调整自己的位置，再次将自己的新位置发送给friendSet中的顶点。

步骤4 重复步骤3，直到达到迭代次数，或者整个系统趋于稳定。

图2 100个节点布局情况

图3 1000个节点布局情况

基于pregel模型的k-friend布局算法（pk-friend布局算法）的伪代码如下。

6 性能测试

本文算法分为单机和并行两个版本。单机版本采用Java语言编写，测试环境为：I7处理器，8 GB内存。并行版本采用Scala语言编写，测试环境为40台高性能计算机组成的小型集群，具体配置为Intel-酷睿I7 CPU，8 GB内存，Spark1.41版本分布式并行计算平台，Hadoop2.6版本。

对于单机版本，笔者测试了100个节点的图数据和1000个节点的平均出度为5的生成图数据。布局效果如图2和图3所示。

效果基本与传统力导向算法无异，其差别人眼很难分辨，因此笔者制定了量化的指标对两种算法进行了对比。因为在大图数据分析的情况下，布局的目的是令邻居节点位置尽量近，非邻居节点之间的距离尽量远，并且忽略关系不紧密的顶点之间的位置关系，所以定义可视化质量度量指标Q如式（1）所示。

其中，E是相互之间存在边的顶点对的集合，F是顶点与它的friendSet中的点分别组成的顶点对的集合。式（1）中，分母表示有边的顶点之间的平均距离，分子表示每个顶点与其friendSet中顶点之间的平均距离，因此，Q值越大说明布局效果越好。

通过随机生成的图数据对比了本文提出的k-friend布局算法和FR算法的性能。参数设置为：迭代次数为200次，退火函数为tn=0.95×tn-1，t1=140，深度值n为3，k为1000。

从图4和图5可以看出，本文算法与FR算法在布局质量上的差距大概只有1%，几乎可以忽略不计，而在计算时间上，本文算法有压倒性的优势，尤其是在顶点数多的情况下，与顶点数目成线性关系，并且斜率也较小。

直观上，本文提出的k-friend布局算法中的friendset的大小对算法的性能是有影响的，当k等于图的顶点数时，就与FR算法等效，当k较小时，算法的速度会很快，但是算法的布局质量就会下降。k又与考虑的邻居的深度层数n有关。因此，本文测试了n值对布局结果的影响，使用爬取到的微博转发信息对算法进行测试。微博是小米手机在2015年1月7日发布的其将在1月15日举办产品发布会的一条微博，微博地址：http://weibo.com/2202387347/BEp EoDfJf?type=repost&retcode=6102#_ rnd1470800271407。布局效果如图6所示，每一条边代表一次转发，每一个顶点代表一个转发的人。

可以看到，随着n的减少，由于斥力计算被减少了，会使得关系不紧密的顶点相对近一些，具体n如何选择，要根据用户的具体需求来确定。

对于并行算法的可扩展性，本文设计节点数增加时算法的计算时间变化情况。使用爬取到的网站链接图，顶点数为201582，边数为230425。输入参数为迭代次数为50次，退火函数为tn=0.95×tn-1，t1=140（即第一次迭代时的最大位移量，与tn=0.95×tn-1对应），n=5。

从图7可以看到，随着处理器核数的增加，计算时间减少。

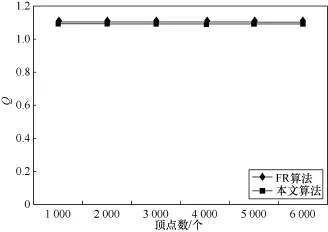
图4 质量对比

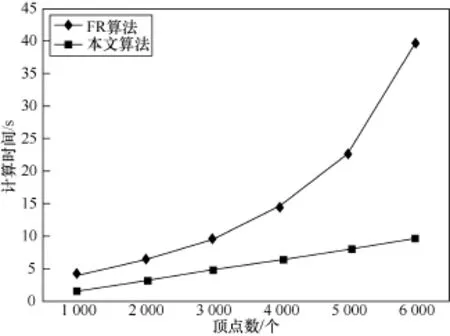
图5 时间对比

图6 布局算法性能对比

图7 分布式版本性能测试

7 结束语

本文提出了k-friend布局算法，通过只计算关联紧密顶点之间的斥力，使得在牺牲少量布局质量的情况下，大幅度提升计算效率，同时也使得该算法的并行化成为了可能。使用分层的策略，既降低了不相邻顶点被放置到相近位置的可能性，又提升了算法的执行效率，而且采用这种策略可以使用户在比较短的时间内看到较概括的上层布局，在用户观察上层布局的同时，计算详细的下层布局，提升了用户体验。最后，使用分布式计算框架BSP框架实现了k-friend布局算法的并行算法，使得图布局算法真正地可以处理海量的图数据。

通过实验发现，本文提出的算法无论是在处理速度上还是处理的数据量上，都优于现有的其他算法，并能够有效地对社交网络数据进行可视化分析。

[1] QUIGLEY A, EADES P.FADE: graph drawing, clustering, and visual abstraction[C]//The 8th Symposium on Graph Drawing, September 20-23, 2000, Colonial Williamsburg, VA, USA.London: Springer-Verlag, 2000: 197-210.

[2] REINGOLD E.Graph drawing by forcedirected placement[J].Software: Practice and Experience, 1991, 21(11): 1129-1164.

[3] HU Y F.Efficient and high quality forcedirected graph drawing[J].Mathematica Journal, 2005, 10(6): 37-71.

[4] HADANY R, HAREL D.A multi-scale algorithm for drawing graphs nicely[J].Discrete Applied Mathematics, 2001, 113(1) : 3-21.

[5] KAMADA T, KAWAI S.An algorithm for drawing general undirected graphs[J].Information Processing Letters, 1989, 31(1) : 7-15.

[6] GAJER P, GOODRICH M T, KOBOUROV S G.A fast multi-dimensional algorithmfor drawing large graphs[J].Computational Geometry: Theory and Applications, 2004, 29(1) : 3-18.

[7] BREITKREUTZ B J, STARK C, TYERS M.Osprey: a network visualization system[J].Genome Biology, 2003, 4(3) : 22-24.

[8] ELMQVIST N, DO T N, GOODELL H, et al.ZAME: interactive large scale graph visualization[C]//IEEE Pacific Visualization Symposium, March 5-7, 2008, Kyoto, Japan.New Jersey: IEEE Press, 2008: 215-222.

[9] BECKER R A, EICK S G, WILKS A R.Visualizing network data[J].IEEE Trans on Visualization and Computer Graphics, 1995, 1(1): 16-28.

[10] TIKHONOVA A, MA K L.A scalable parallel force-directed graph layout algorithm[C]// Eurographics Conference on Parallel Graphics and Visualization, April 14-15, 2008, Crete, Greece.New York: ACM Press, 2008: 25-32.

[11] JACOMY M, VENTURINI T, HEYMANN S, et al.ForceAtlas2, a continuous graph layout algorithm for handy network visualization designed for the gephi software[J].Plos One, 2014, 9(6): e98679.

[12] CHAN S M, CHUA K S, LECKIE C, et al.Visualisation of power-law network topologies[C]// The 11th IEEE International Conference on Networks(ICON2003), September 28-October 1, 2003, Sydney, NSW, Australia.New Jersey: IEEE Press, 2003: 69-74.

Parallel graph layout algorithm for large-scale graph data

CHENG Zhiyuan, BAO Yubin, LENG Fangling
Department of Computer Science of Northeastern University, Shenyang 110819, China

Graph models are modeling tools which are widely used.Data visualization techniques have been widely used as intuitive data analysis tools.Graph layout algorithm is the most critical technique of graph visualization, while there are no effective parallel graph layout algorithms.So to study on visualization of massive graph data is a challenging problem.Aiming at this problem, based on the force-directed layout algorithm and ignoring the repulsion force computation between weakly associated vertexes partially, a k-friend approximate layout algorithm was proposed, and an effective parallel layout algorithm was designed for massive graph data.The experimental results on artificial and real dataset show that the algorithms proposed greatly improve the layout speed.

force-directed algorithm, visualization analysis, social network, parallel layout algorithm

TP391

10.11959/j.issn.2096-0271.2016050