导弹末端弹道光学测量方法研究*

2016-04-08袁震宇钟志通林彬彬

舰船电子工程 2016年1期

关键词：误差分析

袁震宇　钟志通　张　林　林彬彬

(海军大连舰艇学院　大连　116018)

导弹末端弹道光学测量方法研究*

袁震宇钟志通张林林彬彬

(海军大连舰艇学院大连116018)

摘要使用光学测量方法对导弹末端弹道进行测量面临的一个重要问题是,相机标定时所需要处理的视场太大,但根据导弹末端弹道测量对测量精度要求不高的特点,采用透视变换模型对相机进行标定,忽略镜头畸变的影响完成光学测量,算例计算结果和误差分析表明了方法的可行性。

关键词导弹末端弹道测量; 大视场; 透视变换模型; 误差分析

Research on the Optical Measurement of Missile Terminal Ballistic Curve

YUAN ZhenyuZHONG ZhitongZHANG LinLIN Binbin

(Dalian Naval Academy, Dalian116018)

AbstractWhen estimating the missile terminal curve through the optical measurement, a problem had to be faced was that the view area was too large to calibrate, however, based on the characteristic that the high precision was not the most needed, a perspective transform model was used to calibrate the camera, and the aberration of lens was ignored, then an example of optical measurement and its error analysis indicated the feasibility of the method.

Key Wordsmissile terminal curve estimation, large view area, perspective transform model, error analysis

Class NumberV557

1引言

导弹弹道末端测量是导弹武器作战效能评估的一个重要环节。由于导弹速度快,卫星定位数据由于频率不够高使得导弹末端弹道的测量点不够;而使用雷达进行测量成本高,结构复杂,而且雷达一般需要人工操作,不适合在高危险的导弹弹着区使用。近年来,基于双目定位原理的光学测量方法由于其可以实现非接触测量、且测量精度高的优点而被广泛应用于工业控制、外科手术器械精确定位、立体视觉等众多测量领域。

双目定位原理的实质是通过两台相机从不同角度拍摄的图像中恢复出被拍摄物体三维信息的过程。实现该过程一般包括图像获取、相机标定、特征提取与匹配和三维信息恢复几个过程[1～4]。

基于双目定位原理对导弹末端弹道测量是通过在导弹靶标附近适当位置安放的两台相机采集导弹过靶图像,然后通过对两台相机所获取的图像对的处理完成对每对图像中导弹目标的定位,进而拟合导弹的末端弹道。

2图像获取

使用两台带外触发的工业相机对导弹末端过靶图像进行采集,通过使用同一个脉冲触发器对两台相机提供相机快门开合的脉冲信号,以保证两台相机同步采集导弹过靶图像,避免因数据采集不同步造成的测量误差。因为导弹飞行速度特别快,设亚音速的导弹飞行速度为300m/s,相机图像采集频率为25Hz,则若不采用同步触发装置使相机图像采集时机同步,则两台相机图像采集的时间差最大为

对应两个相机图像中导弹的位置之差为

Δs=Δt*300=6m

极大地影响了测量的精度。

3相机标定

相机的成像模型因镜头的畸变等因素的影响,通常是一个非线性的模型,尤其是小焦距的广角镜头,成像的鱼眼现象严重,因此确定相机成像模型的相机的标定过程是一个难点步骤,是影响测量精度一个重要环节。为了对相机的整个视场中的点进行成像模型校正,当前的相机标定方法通常要求已知尺寸的定标参照物几乎充满相机视场,因而当前使用光学测量方法进行高精度测量的测量区域的大小有限,对于大视场条件下,由于无法制作覆盖大视场的定标参照物而难以对相机进行精确标定,因此相关研究较少。

使用光学测量法对导弹末端弹道进行测量,要保证至少有3帧图像捕捉到导弹,则对应的相机视场宽度至少为

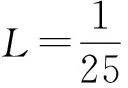
设相机视场长宽比为4∶3,则视场的高度为27m,对于36m×27m宽的视场,必然没有能够覆盖视场的定标参照物。考虑到导弹战斗部的威力较大,常规战斗部一般杀伤半径可达10m,因此,对导弹末端弹道估计存在的误差可能不影响导弹作战效能的评估,同时采用的非短焦镜头畸变较小,可忽略镜头畸变的影响,直接采用透视变换矩阵模型对相机进行标定[5～6]。

透视变换标定方法采用线性针孔摄像机模型。利用投影变换矩阵进行标定,有如下方程[2]:

(1)

其中(Xw,Yw,Zw,1)是空间三维点的世界齐次坐标,(u,v,1)为像素坐标系下点的齐次坐标,将上式展开,消去参数Zc,可得如下含有参数mij的两个方程:

XWm11+YWm12+ZWm13+m14-uXWm31

-uYWm32-uZWm33=um34

(2)

XWm21+YWm22+ZWm23+m24-vXWm31

-vYWm32-vZWm33=vm34

(3)

如果已知三维世界坐标和相应的图像坐标,将变换矩阵看作未知数,则共有12个未知数。对于每一个目标点,都有如式(2)、式(3)两个方程,一般可假设m34=1,则共有11个未知数,设有n个目标点,其世界坐标为(Xwi,Ywi,Zwi),i=1,2,…,n,对应的图像坐标为(ui,vi),i=1,2,…,n,则可得2n个方程,联立这些方程可得一个方程组,并写出矩阵形式如下:

T*M=B

(4)

其中:

M=[m11…m14m21…m24m31…m33]T

B=[u1…unv1…vn]T

若n≥6,则该方程组是个超定线性方程组,利用最小二乘法可以很容易求出上述线性方程组的解:

M=(TTT)-1TTb

(5)

采用更多的已知点,可以使方程的个数大大超过未知数的个数,用最小二乘法求解可以降低误差造成的影响。

4特征点匹配

通过对两个摄像机的标定可确定两个相机的投影变换矩阵,下步即提取目标在左右相机成像面上的特征点,并将对应特征点匹配,进而获得目标特征点的深度信息。

由于已知两个摄像机的内外部参数,对于一个图像上的某个特征点,它在另外一个图上的特征点的位置满足极线约束[2]:

(6)

因此根据极线约束可进行自动特征点匹配。

5三维坐标计算

设通过摄像机标定和立体匹配确定了空间点P在左右两个摄像机成像平面上的图像坐标分别是p1(ul,vl),p2(ur,vr),那么,根据摄像机成像模型,可得[3]

(7)

(8)

其中,Ml、Mr为左右两个摄像机的投影矩阵,ml34=mr34=1,(x,y,z)为欲求的P点的三维坐标。

消去zl,zr得:

(9)

将上式化简得:

AP=b

(10)

其中

P=[xyz]T

根据最小二乘,解得空间点P的坐标为

P=(ATA)-1ATb

(11)

因此完成了对空间点P的定位。

6算例分析

对制作的模型从不同角度采集两幅图像如图1、图2所示,图中圆圈中的交叉点为已知世界坐标的点,用于相机的标定,方框中的角点则为已知世界坐标的测试点,用于分析该光学测量方法的误差。

图1　左图

图2　右图

图中三列圆圈内交叉点的世界坐标由左到右如表1。

表1　标定点世界坐标

左右图中圆圈内交叉点图像坐标如表2、表3所示。

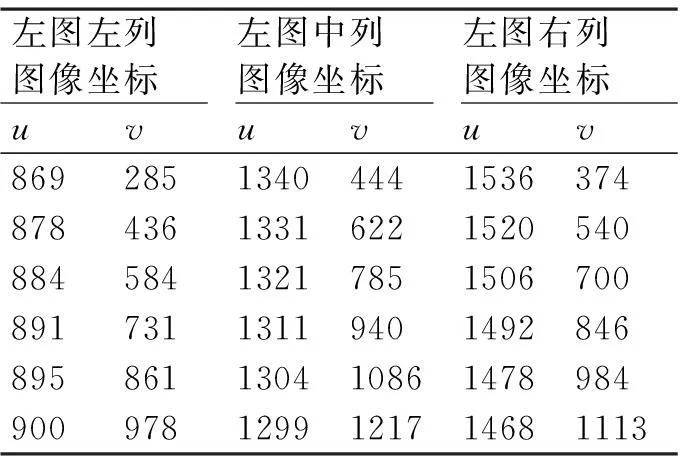
表2　标定点在左相机图像坐标

表3　标定点在右相机图像坐标

根据式(3)、式(4)可得左图对应的相机的投影矩阵为

右图对应的相机的投影矩阵为

图中五个测试点在左右两图中的图像坐标如表4所示。

表4　测试点在两图中的图像坐标

根据获得的两个相机的投影矩阵以及测试点在左右两图中的图像坐标,即可计算出测试点世界坐标的估计值[7],如表5所示。

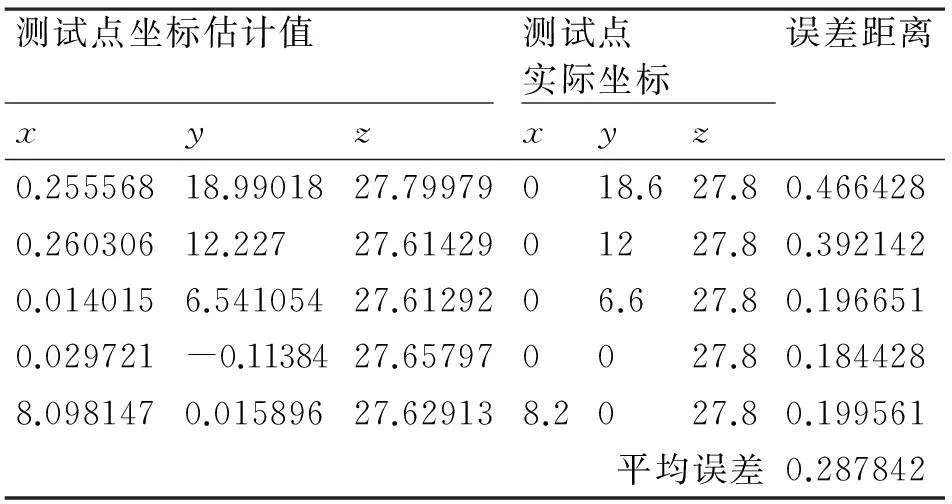
表5　测试点实际坐标及估计值

7误差分析

根据光的直线传播原理可设实验中各标定点、测试点的世界坐标单位为m,则实验中相机的视场不小于36m×27m的视场大小,由测试结果误差距离可以看出,测试点测量的平均误差距离为0.288m,相对于导弹战斗部10m左右量级的杀伤半径,该误差是可以接受的,同时计算左右两相机投影矩阵时进行最小二乘估计使用的系数矩阵的条件数分别为7.3×104和8.2×104,而计算测试点世界坐标是进行最小二乘估计使用的系数矩阵的条件数如表6所示。