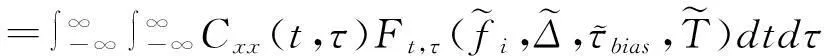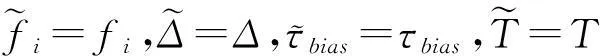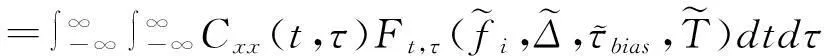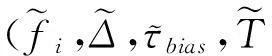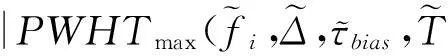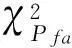基于周期Wigner-Hough变换的线性调频连续波信号检测算法*

宦爱奇　刘　锋　王泽众

(1.海军航空工程学院　山东　264001)(2.海军装备研究院　北京　100249)



基于周期Wigner-Hough变换的线性调频连续波信号检测算法*

宦爱奇1刘锋1王泽众2

(1.海军航空工程学院山东264001)(2.海军装备研究院北京100249)

摘要提出了一种周期Wigner-Hough变换(PWHT)对线性调频连续波(LFMCW)信号的检测算法。分析了线性调频连续波信号的PWHT及其性质,并对无先验知识条件下的LFMCW信号检测问题进行研究,给出了基于PWHT的LFMCW信号检测流程。仿真验证了该算法由观测时间带来的检测性能增长与噪声方差不为1时的检测性能变化趋势。

关键词周期Wigner-Hough变换; 线性调频连续波; 信号检测

Linear Frequency Modulation Continuous Wave Radar Signal Detection Algorithm Based on Periodic Wigner-Hough Transform

HUAN Aiqi1LIU Feng1WANG Zezhong2

(1. Naval Aeronautical and Astronautical University, Yantai264001) (2. Naval Armament Research Institute, Beijing100249)

AbstractA linear frequency modulation continuous wave radar signal detection algorithm which was based on periodic Wigner-Hough Transform was proposed. Firstly, the properties of the periodic WHT of a linearly frequency modulated continuous wave signal were analyzed. Secondly, LFMCW signal detection with no prior knowledge was studied. Thirdly, the workflow of the application of the algorithm was proposed. Finally, the increase in detection performance by observation time and the detection performance variation trend when noise variance wasn’t 1 were verified by simulation.

Key WordsPWHT, linear frequency modulated continuous wave, signal detection

Class NumberTN95

1引言

低截获概率(Low Probability Intercept,LPI)雷达信号具有波形复杂、功率低、带宽宽等特点,雷达侦察接收机很难对其进行可靠的识别。而线性调频连续波(Linear Frequency Modulated Continuous Wave,LFMCW)信号是LPI雷达常采用的信号形式,它不仅具有良好的距离/速度分辨力和测量精度,还具有良好的抗干扰能力和低截获性能。在雷达侦察中,如何对这类信号进行快速有效地识别已成为一大难点,也是近几年电子侦察方向研究的一大热点[1]。

为了更好的处理此类信号,文献[2～5]、[6～11]分别基于镜像滤波器组(QMFB)、WHT、FRFT和Choi-Williams分布(CWD)等算法,对LFMCW信号的检测与参数估计问题进行了研究,但是效果都不理想。其中,QMFB不具抗噪功能,需要首先对信号进行消噪处理,导致信号检测与参数提取能力受消噪能力影响较大;由于受多分量LFM周期交叉项的影响,基于WHT和FRFT的方法在低信噪比条件下很难提取LFMCW的信号特征并进行识别,且在多分量连续波信号存在的条件下,不可避免地受到交叉项干扰;CWD可以避免交叉项的影响,但是它的时频分辨力下降比较严重,从而降低了LFMCW信号特征提取和识别能力。

周期WHT是2010年由Francis G. Geroleo[12]提出的结合WHT和雷达信号处理中相干积累思想的算法。该算法将LFMCW信号的LFM周期性特征考虑在内,可以实现一次观测时间内的周期性能量积累,通过寻找LFMCW的周期性调制特征,实现对LFMCW信号的检测。同时,由于在周期WHT域LFMCW信号特征较WHT域特征更加清晰、直观,较后者更适合LFMCW雷达信号的识别。周期WHT算法比较新,对其离散化算法性能分析以及实际应用还有待研究。

本文对雷达侦察中采用周期WHT进行LFMCW信号的检测与参数估计的问题进行了深入研究,以期更好地解决LFMCW信号在低信噪比条件下的检测与参数估计问题。

2LFMCW信号及其PWHT

对于脉冲雷达信号,由于其相对较高的峰值功率,即使在时域或频域检测不到信号,往往也可以通过特定变换域的峰值对其进行检测。然而,连续波雷达信号比脉冲雷达信号的峰值功率要小得多,一般仅有后者的1%左右。所以,即使对于脉冲信号有良好效果的特定变换域检测,对于连续波信号来讲,在相对更低的信噪比条件下是无法进行有效检测的。

周期WHT算法将相干积累的思想引入雷达信号侦察系统的LFMCW弱信号检测问题中,可以实现一次观测时间内LFMCW不同调制周期信号能量的积累,较已有的基于WHT的LFMCW信号检测算法有更好的检测能力。

LFMCW信号是LFM脉冲信号的周期拓展,由有限时间长度内多个LFM脉冲信号的时间连续组合而成。设一次接收机观测时间为Tobs,T为一个LFM调制周期的时间长度,则观测时间内的LFM调制脉冲数M=Tobs/T。LFMCW信号模型如下所示:

x(t)=Aej(φ+2πfit+πΔ[mod(t+τbias,T)]2)

(1)

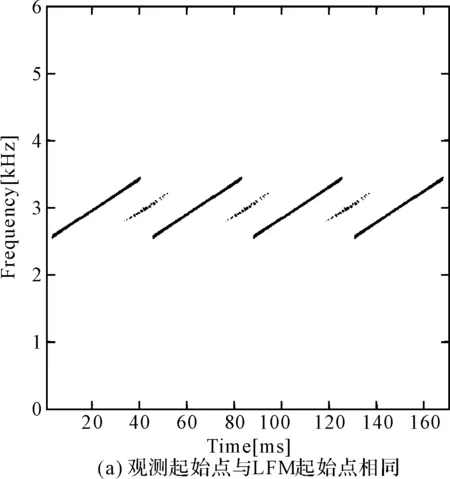
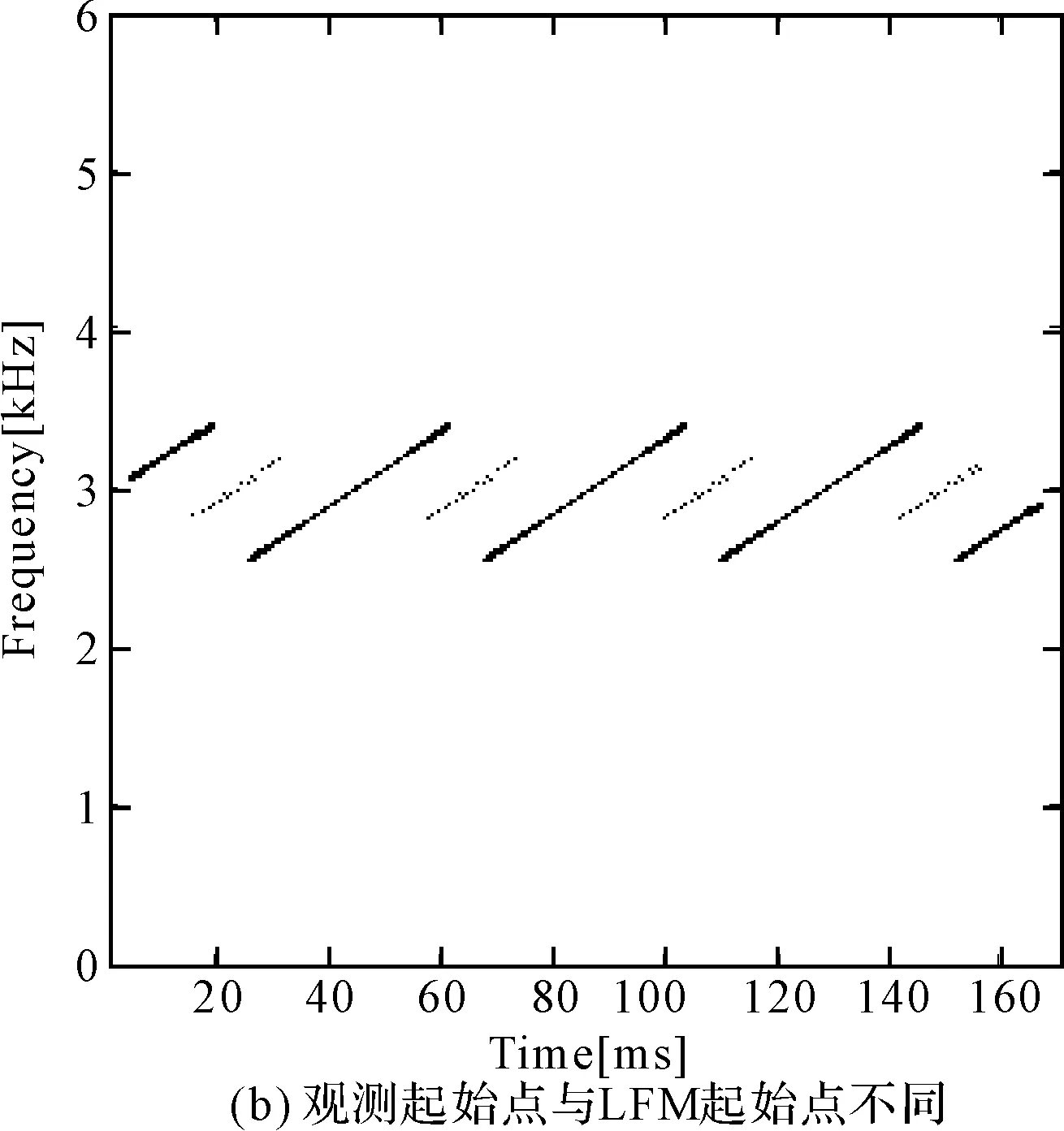
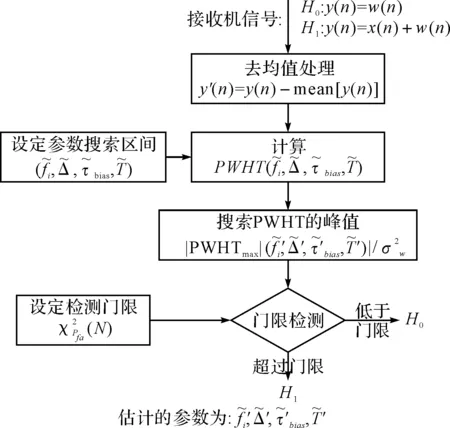
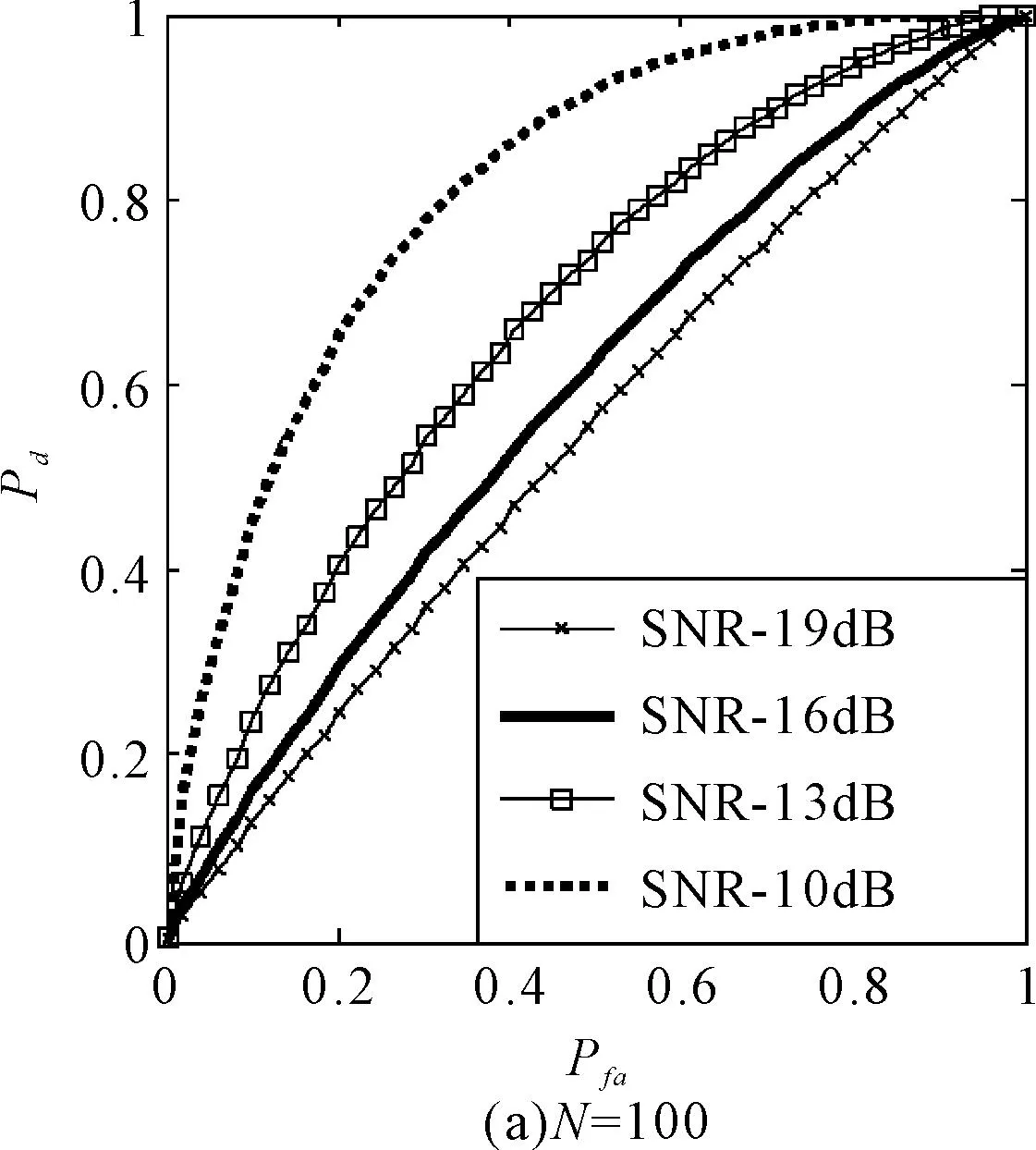
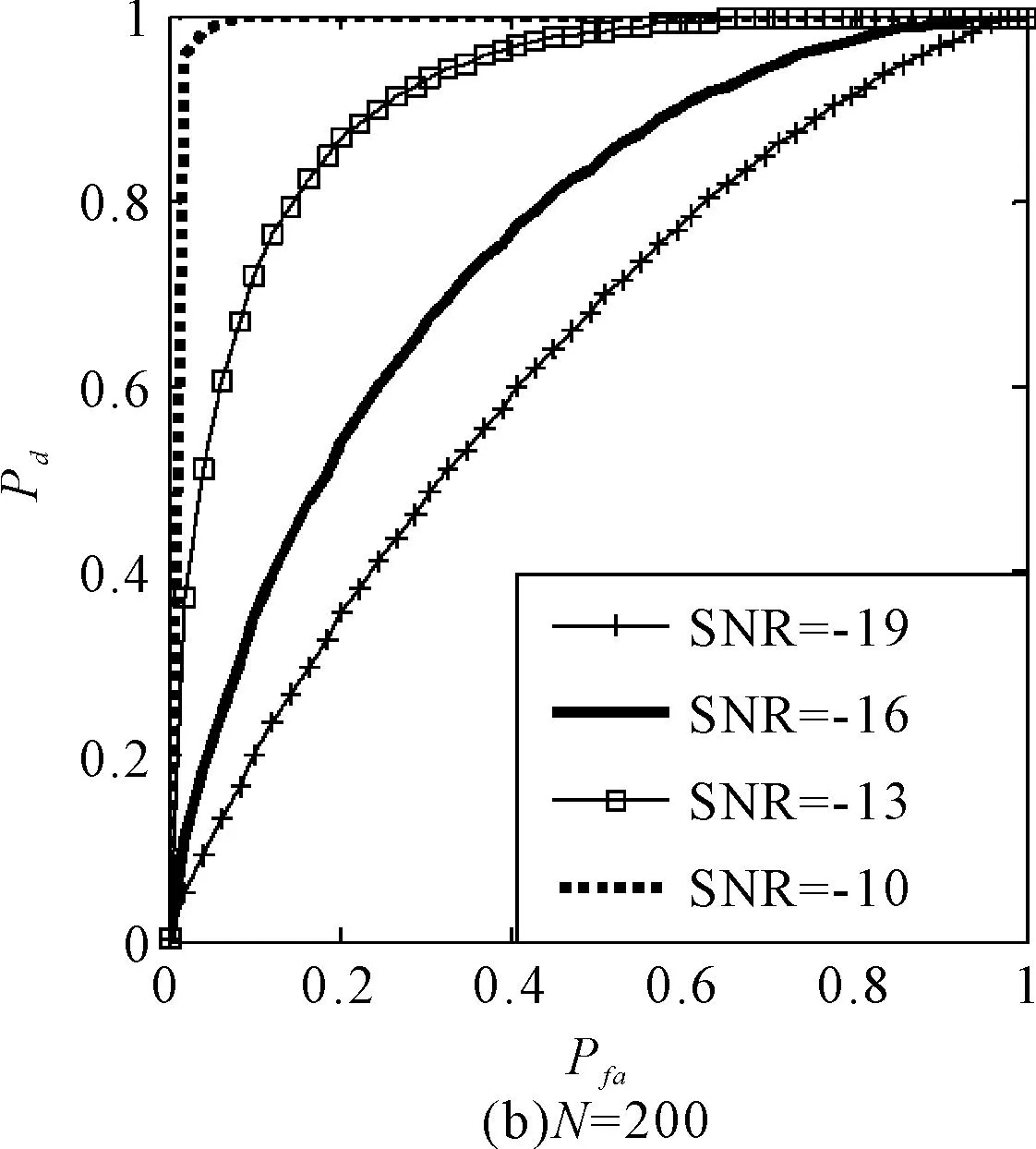
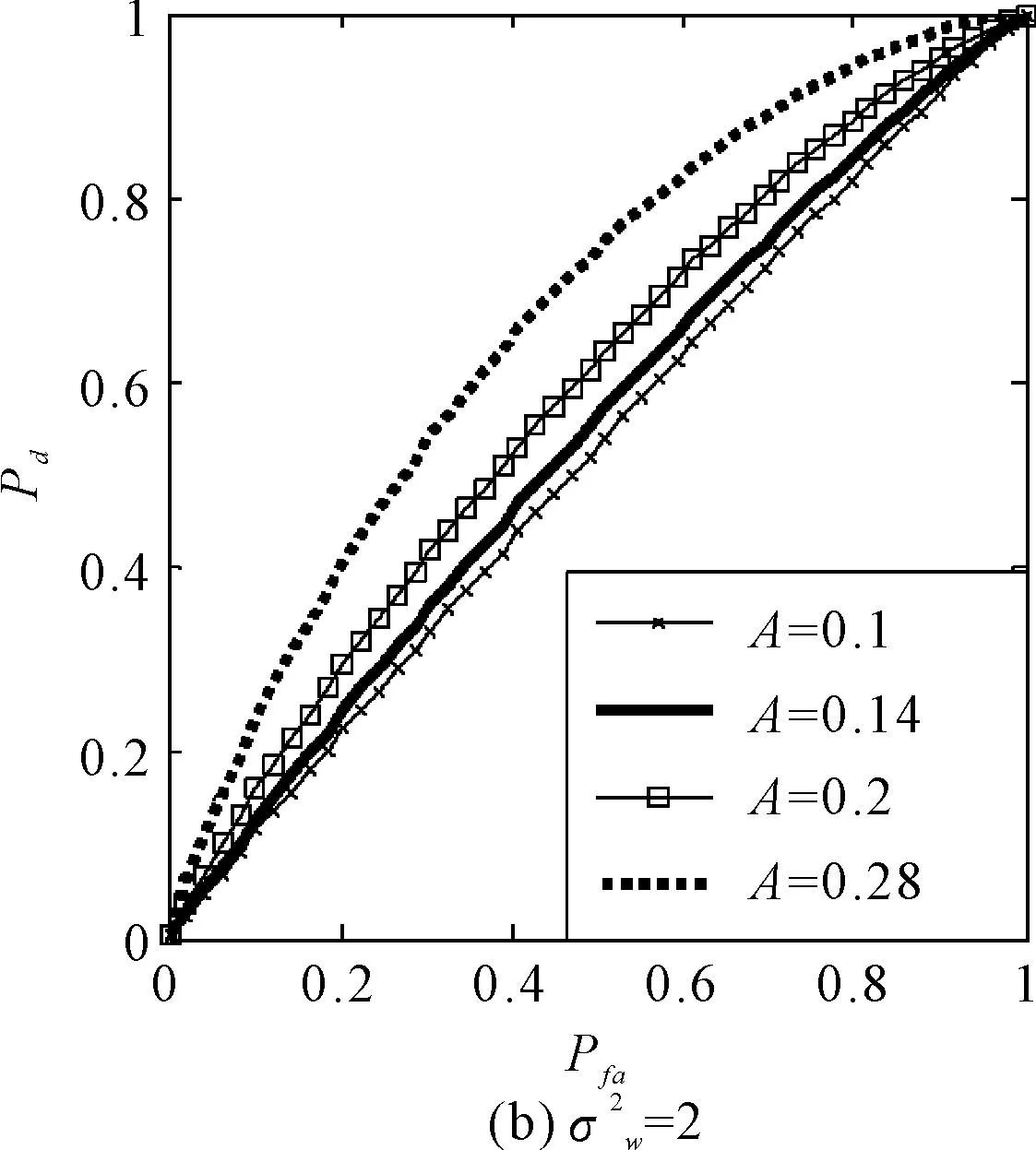
式中:A为幅度,φ为初始相位,fi为初始频率,Δ为调频率,mod(·)表示取模算子,mod(a,b)表示a除以b所得的余数。τbias为信号的时间偏移,并且0≤τ

图1　基于Pseudo Wigner-Ville变换的LFMCW信号时频分布

令M=4,通过Pseudo Wigner-Ville变换,可以得到LFMCW信号的时频分布特征(如图1),图1(a)为观测起始点与LFM起始点相同,图1(b)表示两者起始点存在1/2调制周期的时间偏移。由图1都可以看出,LFMCW信号在时频域表现出明显的周期线性调频特征。

设

Ft,τ(fi,Δ,τbias,T)

(2)

定义LFMCW信号的周期WHT为

(3)

(4)

3LFMCW信号检测与参数估计算法研究

对于雷达侦察系统而言,无法提前预知敌方雷达信号的先验知识,在这种非合作条件下,由于输入噪声存在不确定性,信号的检测问题可以采用统计学方法,通过门线检测描述LFMCW信号检测过程。设置门限的目的在于将检测判决输出划分为信号区和噪声区,即将信号检测问题等效为一个二元假设检验问题。

设待检测信号x(n)为LFMCW信号,则二元假设检验问题可以表示为

H0:y(n)=ω(n)只有噪声

H1:y(n)=x(n)+ω(n)信号加噪声

式中:ω(n)为噪声,x(n)为与噪声独立的LFMCW信号,n=1,2,…,N,N表示采样点的数量。

由于通常无法事先确定先验概率和代价因子,所以采用纽曼-皮尔逊准则设计检测器,使得在确定的虚警概率Pfa的情况下,检测概率Pd达到最大。在周期WHT域,检验统计量I为

(5)

则虚警概率Pfa为

(6)

检测概率为Pd为

(7)

式中:β表示检测门限。

门限β的选取可以通过周期WHT域H0条件下I的概率密度函数p(I|H0)和设定的虚警概率Pfa在式(6)中取得。将选取后的门限β代入式(7),结合H1条件下I的概率密度函数p(I|H1),可以得到最佳检测系统的检测概率Pd。所以,H0条件下I的概率密度函数p(I|H0)和H1条件下I的概率密度函数p(I|H1)的表示起关键作用。

4检测与参数估计流程

在加性高斯白噪声中,雷达侦察接收机基于PWHT的LFMCW信号检测与特征参数估计流程如图2所示。

图2　检测与参数估计流程图

具体流程描述为:

步骤一:对离散采样信号做均值化处理:y′(n)=y(n)-mean[y(n)]。其中mean[·]为均值算子。

5仿真实验与分析

5.1观测时间不同周期WHT的检测性能

设采样点数N=100、N=200(在采样频率固定的前提下,对应不同的观测时间),噪声为为0均值,方差为1的高斯白噪声,输入信噪比为-19dB,-16dB,-13dB,-10dB。

取虚警概率Pfa=0～1,可以得到基于周期WHT检测算法的接收机特性曲线(如图3)。由图3可以看出:随着信噪比的改善,基于周期WHT的接收机特性曲线在更低虚警概率下具有更好的检测能力;采样点数越多(即观测时间越长),基于周期WHT的接收机特性曲线在更低虚警概率下具有更好的检测能力。

图的加性高斯白噪声中周期WHT的ROC

仿真实验证实了噪声为为0均值,方差为1的高斯白噪声条件下,基于周期WHT的LFMCW检测算法随着观测时间增长(对应了采样点数增多)而带来的检测能力的改进。

5.2一般噪声条件下周期WHT的检测性能

将条件推广到一般的情况下,设采样点数N=100,噪声是均值为0,方差为0.5和2的高斯白噪声,信号振幅A为0.1、0.14、0.2和0.28。取虚警概率Pfa=0～1,可以得到方差不为1的加性高斯白噪声条件下的基于周期WHT检测算法的接收机特性曲线(如图4)。由图4和图3(a)可以看出:随着噪声方差由0.5到1再到2,接收机的检测能力逐渐下降。在方差为2时,对LFMCW的检测能力基本上比较弱了。

图≠1加性高斯白噪声条件下周期WHT的ROC

仿真实验证实了方差不为1的高斯白噪声条件下,基于周期WHT的LFMCW检测算法随着噪声方差增长(对应了信噪比的降低)而带来的检测能力的退化。

6结语

本文对周期WHT在LFMCW信号检测与参数估计进行了研究,采用基于周期WHT的LFMCW信号的检测与参数估计算法,提出了加性高斯白噪声背景下,周期WHT域LFMCW信号的检

测与参数估计算法,给出了LFMCW信号检测的参数估计流程,并对周期WHT域的LFMCW信号的检测性能进行了仿真验证。仿真结果表明,随着观测时间的增长,基于WHT的LFMCW信号检测算法检测性能增长;随着信号噪声方差的增长(信噪比的降低),算法检测性能随之降低。

参 考 文 献

[1] WIRTH W D. Polyphase coded CW radar[C]//Proceedings of the IEEE Fourth International Symposium on Spread Spectrum Techniques and Applications. Mainz,1996:186-190.

[2] 徐会法.基于FrFT的一类低截获概率雷达信号截获与识别研究[D].烟台:海军航空工程学院,2011.

[3] D. B. Copeland, P. E. Pace. Detection and analysis of FMCW and P4 polyphase LPI waveforms using quadrature mirror filter trees[J]. 2002 IEEE International Conference on Acoustics Speech and Signal Processing. Orlando,2002,4:3960-3963.

[4] Qi Lin, Tao Ran, Zhou Si-yong, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China Ser.F.,2004,47(2):184-198.

[5] H. I. Choi, W. J. Williams. Improved Time-Frequency Representation of Multicomponent Signals Using Exponential Kernels[J]. IEEE Trans. on Acoustics, Speech, and Signal Processing,1989,37(6):862-871.

[6] S. Barbarossa. Analyses of multicomponent LFM signals by a combined Wigner-Hough transform[J]. IEEE Transactions on Signal Processing,1995,43(6):1511-1515.

[7] S. Barbarossa, A. Scaglione, S. Spalletta. Adaptive suppression of wideband interferences in spread-spectrum communications using the Wigner-Hough transforms[J]. IEEE International Conference on Acoustics, Speech, and Signal Processing,1997,5:3861-3854.

[8] 孙晓昶,皇甫堪.基于Wigner-Hough变换的多分量LFM信号检测及离散计算方法[J].电子学报,2003,31(2):1-4.

[9] 梁红,胡旭娟,朱云周.基于RSPWVD-Hough的多分量LFM信号检测[J].系统仿真学报,2007,13:3030-3032.

[10] 夏云龙,朴胜春,付永庆.一种基于时间反转镜和Wigner-Hough变换的线性调频信号检测方法[J].中南大学学报(自然科学版),2009,40(3):719-724.

[11] 刘锋,孙大鹏,黄宇,等.基于改进Wigner-Hough变换的多分量LFM信号特征提取[J].北京理工大学学报,2008,28(10):914-917.

[12] F. G. Geroleo, M. B. Pearce. Detection and Estimation of Multi-Pulse LFMCW Radar Signals[C]//2010 IEEE International Radar Conference,2010:1009-1013.

中图分类号TN95

DOI:10.3969/j.issn.1672-9730.2016.01.014

作者简介:宦爱奇,男,硕士研究生,研究方向:雷达侦察信号处理。刘锋,男,博士,教授,博士生导师,研究方向:电子信息战理论及应用。王泽众,男,博士,研究方向:复杂调制信号截获与识别。

*收稿日期:2015年7月8日,修回日期:2015年8月29日