静力弹塑性分析在框架结构中的运用
2016-04-07汤晓刚吕冬春
汤晓刚 吕冬春
(安徽华电工程咨询设计有限公司,安徽合肥 230022)
静力弹塑性分析在框架结构中的运用
汤晓刚吕冬春
(安徽华电工程咨询设计有限公司,安徽合肥230022)
摘要:阐述了静力弹塑性分析方法的基本原理,以某框架结构为例,利用有限元软件ETABS,对该结构进行了静力弹塑性分析,评估了结构的抗震性能,指出这种静力弹塑性分析方法具有较好的工程实用价值,发展前景广阔。
关键词:静力弹塑性分析,能力谱法,框架结构
弹塑性时程分析法和静力弹塑性分析法是混凝土结构非线性地震反应分析的两种主要方法。其中弹塑性时程分析法是弹塑性分析最为可靠的方法之一,但由于地震作用的随机性,结构在随机的地震作用下,恢复力模型是不确定的,所以限制了弹塑性时程分析法的应用。而静力弹塑性方法即推覆分析方法,可在较短的时间里对结构进行分析,通过观察塑性铰的产生与发展,可以找出结构的薄弱环节,具有较高的工程实用价值[1]
1 静力弹塑性分析方法的基本原理
静力弹塑性分析是沿结构高度施加一定形式的模拟地震作用的侧向荷载,等效侧向荷载强度由小到大逐步增强,使结构由弹性阶段逐步进入弹塑性阶段并分析结构的非线性性能,由此判定结构和构件是否满足在罕遇地震作用下的抗震设防要求。
结构进行Pushover分析其加载步骤[2-4]:
1)建立结构分析模型,求出梁两端的极限弯矩、极限转角和极限承载力,柱M—N关系曲线上的轴压、平衡和纯弯的控制点。其模型包括对结构强度、刚度、稳定性等有较大影响的构件。然后施加竖向重力荷载进行静力分析,将分析得到的应力作为下一步分析的基础并储存。2)初始屈服点应力分析。施加水平地震作用,对结构进行反应谱动力分析,将得到的结构应力与上一步分析结果进行叠加,找出结构中达到屈服应力或接近屈服应力的构件。计算一个比例α1,使得施加α1倍的最大初始加速度时,结构恰好有某些构件进入屈服状态,即结构出现塑性铰。将分析的应力结构储存并作为下一步分析的初始值,即:初始应力+原先反应谱应力×α1=屈服点应力。3)对上一步中进入屈服阶段的构件端部施加塑性铰,修改结构的刚度,算出此时结构的自振周期等,对新的结构施加水平荷载,重复上一步的计算方法得出一个比例α2。此时,上一步计算应力+本步骤计算应力×α2作为下一步应力计算初始值。4)使用上述方法求出比例α3,α4,…,αn,第n步为结构达到目标位移或塑性铰过多形成机构。即:步骤(n-1)+步骤(n)×αn=屈服(n);αn的总和αi为该结构的强度系数,当αi<1.0时,表示结构在指定水平地震作用下会发生破坏,结构不安全。当αi>1.0时,表示结构在指定水平地震作用下安全可靠。
2 某框架结构的能力谱法分析
如图1所示,某工程为规则的10层钢筋混凝土框架结构,板厚120 mm,结构层高3 m,柱截面尺寸:650 mm×650 mm(1层~。5层),550 mm×550 mm(6层~10层),梁截面尺寸:250 mm× 500 mm,250 mm×400 mm。抗震设防烈度为:8度(0.2g),工程场地类别:Ⅱ类,设计地震分组:第一组,楼层均布恒荷载取值: 4.8 kN/m2(楼面),7.0 kN/m2(屋面),楼层均布活荷载取值2.0 kN/m2(楼面),0.7 kN/m2(不上人屋面),考虑X,Y向的风荷载作用,基本风压取值:0.45 kN/m2。混凝土强度等级:C35,钢筋强度等级:fy=360 N/mm2,fyv=210 N/mm2。

图1 框架结构平、立面示意图
2.1结构计算模拟方法
利用ETABS软件进行建模,假定楼板平面内刚度为无穷大[5-8]。弹性分析过程中,框架结构梁柱假定为线弹性单元;在进行静力弹塑性(Pushover)分析时,通过定义梁柱非线性铰来模拟梁柱的非线性单元,其中框架柱单元采用软件提供的PMM型轴力弯矩塑性铰,梁单元塑性铰模拟时,不考虑轴向力对截面抗弯承载力的影响,即采用软件提供的M3主弯矩铰类型,使用FEMA推荐的恢复力特征曲线作为本算例杆件的恢复力特征曲线,如图2所示。
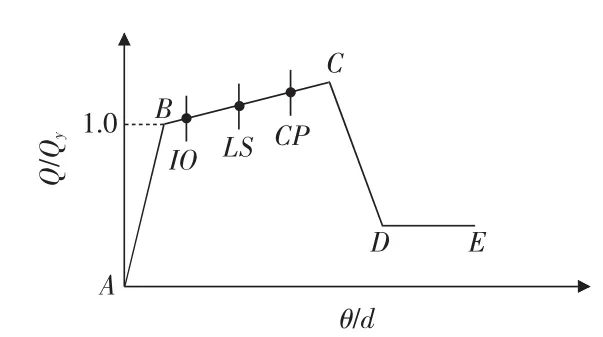
图2 FEMA推荐的非线性恢复力特征曲线
点B代表屈服,在B点之前铰处于刚性状态,无塑性铰,没有塑性变形,BC段是铰处于塑性变形阶段,到达C点时铰达到Pushover分析的极限承载力,CD段铰的承载力逐渐下降,D点为Pushover分析的残余强度,E点则表示铰完全失效。点IO,LS,CP分别代表铰能力水平的几个控制点,其中IO表示立即使用,LS表示生命安全,CP表示防止倒塌。在进行Pushover分析后,可以通过查看软件中变形形状选项来查看结构塑性铰的变化和分布情况,从而判断结构在地震作用下能否达到预定的能力目标。
2.2荷载—位移曲线
软件分析过程中,推覆至位移值600 mm,即0.02结构总高度,构件卸载方法为全结构卸载方法,几何非线性效应为考虑P—Δ效应[9]。可绘制相应的荷载—位移曲线即基底剪力—顶点位移曲线或结构能力曲线,如图3所示。由图可以看出进行推覆分析时结构承载力的变化情况,进入塑性变形后,结构有较长的硬化段才进入屈服段,结构有较大的能量储备。当剪力到达最大值后,基底剪力突然减小,随即结构失效[10],此时的基底剪力为3 401.5 kN,顶点位移为359.2 mm。
2.3能力谱法—结构性能点的确定
1)将结构Pushover分析得到的基底剪力—顶点位移曲线转化为能力谱曲线。以谱位移Sd(C)为横坐标,谱加速度Sa(C)为纵坐标可得到该算例结构能力谱曲线,如图4所示。
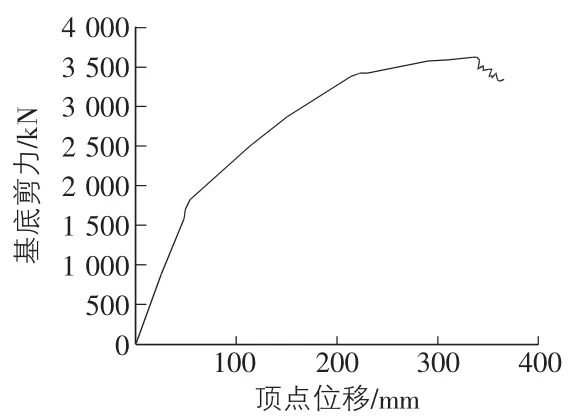
图3 Y向结构能力曲线
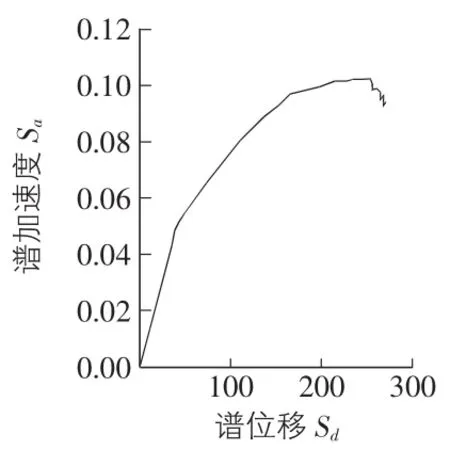
图4 Y向结构能力谱曲线
2)等效周期Teff和等效阻尼比的确定是依据等面积原则,图5,图6分别为等效双线型能力谱曲线和附加阻尼比计算参数图示。
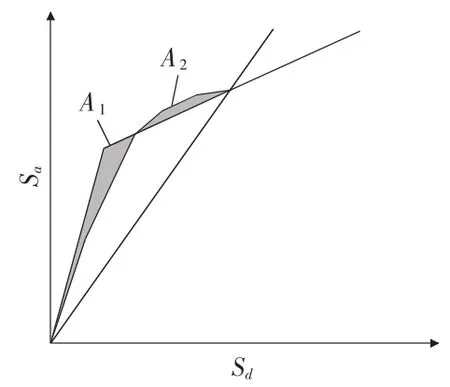
图5 等效双线型能力谱曲线
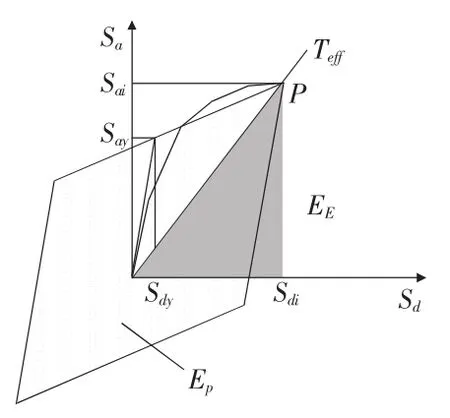
图6 附加阻尼比计算参数示意图
3)如图7所示,能力谱曲线和需求谱曲线的交点为结构在地震作用下的性能点,性能点坐标(Sdt,Sat)=(272.1 mm,0.194 g)。
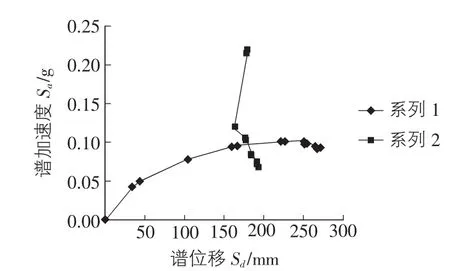
图7 结构性能点示意图
2.4能力谱法—结构性能的评定
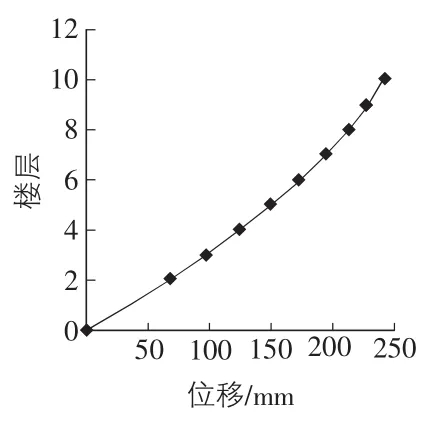
图8 结构性能点处楼层—位移曲线

图9 结构性能点处楼层—层间位移角曲线
根据以上分析对结构性能评价,采用数值插值的方法可求出相应的楼层位移,表1为性能点处各楼层的位移,如图8所示。根据楼层位移可得到Pushover分析各步楼层的层间位移角,采用插值方法可求出性能点处的层间位移角,表2为性能点处各楼层的层间位移角,如图9所示。

表1 性能点处楼层位移 mm

表2 性能点处各楼层的层间位移角 rad
由图9可知该结构性能点处的最大层间位移角在第1层,其数值为1/84,小于规范规定的1/50的限制。因此,在大震作用下,结构Y向能满足“小震不倒,中震可修,大震不倒”的抗震设防要求。
3 结语
1)用ETABS软件对结构进行静力弹塑性分析来评定结构抗震性能时,具有操作简单、概念明确清晰等优点。在对结构抗震性能进行评估时,只需求出结构层间位移角并与规范的规定值进行比较,就可得出结论。2)通过对结构的分析结果和后续处理可以看出结构的塑性铰分布及层间位移角的大小,用能力谱法分析得出结果符合结构的实际情况。3)通过对梁柱塑性铰观察可以看出结构的塑性铰是从梁端开展并逐步向柱端发展的,说明算例是按照抗震规范上的“强柱弱梁”的思想设计的,结构的塑性铰开展情况说明结构存在薄弱层,薄弱层处的结构设计有待进一步加强,但是结构的塑性铰分布仍不是很充分,说明结构具有大震作用下的抗震性能。
综上可知,静力弹塑性Pushover分析方法会有较好的发展前景,随着人们对地震作用机理及结构在地震作用下的反应等方面认识和研究的突破,该分析方法的合理性和工程实用性会变得更加明显。
参考文献:
[1]小古俊介.日本基于性能结构抗震设计方法的进展[J].建筑结构学报,2000,21(1):37-51.
[2]Applied Technology Council.Seismic evaluation and retrofit of concrete buildings.ATC-40,1996.
[3]Federal Emergency Management Agency.NEHRP Guidelines for the seismic rehabilitation of buildings.FEMA273,1997.
[4]王亚勇,戴国莹.建筑结构抗震设计规范算例[M].北京:中国建筑工业出版社,2006:25-27.
[5]李应斌,刘伯权,史庆轩.基于结构性能的抗震设计理论研究与展望[J].地震工程与工程振动,2001,21(4):12.
[6]叶燎原,潘文.结构静力弹塑性分析(push-over)的原理和计算实例[J].建筑结构学报,2000,20(2):37-43.
[7]叶献国.多层建筑结构抗震性能的近似评估—改进的能力谱方法[J].工程抗震,1998,12(4):10-14.
[8]叶献国,周锡元.建筑结构地震反应简化分析方法的进一步改进[J].合肥工业大学学报,2000,23(2):149-153.
[9]侯爽,欧进萍.结构Pushover分析的侧向力分布及高阶振型影响[J].地震工程与工程振动,2004,24(3):89-97.
[10]汪大绥,贺军利,张凤新.静力弹塑性分析(Pushover Analysis)的基本原理和计算实例[J].世界地震工程,2004,20 (1):45-53.
作者简介:汤晓刚(1984-),男,工程师;吕冬春(1979-),男,工程师
收稿日期:2015-10-29
文章编号:1009-6825(2016)01-0046-03
中图分类号:TU323.5
文献标识码:A
