一种借助虚拟观测降低单站测向误差的方法

郁　涛

(中国电子科技集团公司第五十一研究所，上海 201802)



一种借助虚拟观测降低单站测向误差的方法

郁涛

(中国电子科技集团公司第五十一研究所，上海 201802)

摘要针对短基线测向精度难以提高的问题，提出了一种借助虚拟观测降低单站测向误差的方法。利用一个实测单站的相差定位测量结果，由三角函数关系可得到异地虚拟站点相对于目标的径向距离，由此得到异地虚拟站点与实测单站之间的虚拟程差，在此基础上，分别分析了借助虚拟单、双站的测向方法。误差分析表明，通过选择合适的虚拟基线长度，能有限地提高测向精度。

关键词测向；相差定位；虚拟观测；长基线；无源定位

A Method of Reducing Single-station DF Error with the Help of Virtual Observation

YU Tao

(The51stResearchInstituteofCETC，Shanghai201802，China)

AbstractIn view of the difficulties of improving the accuracy of short-baseline direction finding direction finding (DF)，this paper proposes a method of reducing single-station DF error with the help of virtual observation.By using the phase difference location result from a test site，the radial distance from virtual site of different station to the target can be derived by circular function.Thus，the virtual path difference can be obtained between the test site and the virtual site of different place.On this basis，the DF method is analyzed respectively based on virtual single and double stations.The error analysis shows that the DF precision can be slightly improved by selecting appropriate length of virtual baseline.

Key wordsDF;phase difference location;virtual observation;long baseline;passive location

0引言

相差测向的精度是和基线长度成正比的，在相差测量的均方根误差已确定的情况下，为提高测向精度可采用的一个主要方法就是增加基线长度。尽管从纯理论分析的角度，增加基线长度能提高测向精度，但事实上现有的困难在于：在增加基线长度后，原有的对长度仅为几十个波长的短基线解相位模糊的算法将无法继续利用。同时，在长基线情况下，阵列间相差测量的精度亦难以得到保证，一个难以克服的问题是因微波频段相差测量的敏感性，在基线长度上的微小变化就有可能带来巨大的测量误差。因此，企图通过直接增加基线长度以实现长基线相差测向的做法似乎不满足目前工程实际可实现的条件[1-7]。

事实上，相差定位亦属于程差定位的范畴，如果能间接获取与长基线相对应的站点间的程差，则就有可能避开解相差模糊等问题。作为一种探索，本文研究了一种借助虚拟观测方法实现对基线长度的拓展，并用以提高测向精度的方法。

1虚拟程差

1.1虚拟布站

虚拟多站定位阵列如图1所示。

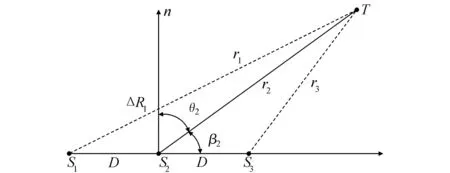
图1　虚拟多站定位阵列

对图1所示的三站定位阵列，考虑2种虚拟拓展基线的方法：① 假设左右两侧都设置有虚拟站点，中间站点安置有一个使用短基线的一维双基相差测量阵列；② 仅在实测站点的右侧安置虚拟站点。左右虚拟2站相对目标的径向距离都是通过中间实测站点的定位结果得到的。

1.2短基线相差测距

一维双基阵如图2所示，以一维双基阵中点为基准的短基线相差测距解是[8,9]:

(1)

式中，d为短基线长度；Δri为基于相差测量的程差；

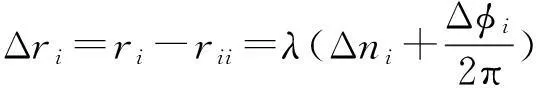
(2)

式中，Δni=ni-ni+1为程差所包含的波长整周数；Δφi=φi-φi+1为两阵元之间的相位差。

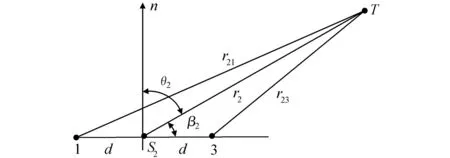
图2　一维双基阵

为和利用虚拟基线三维定位阵列中的径向距离相区别，实测站点内基于短基线阵列得到的径向距离采用双下标表示。

1.3借助虚拟程差的测向

由中间实测站点的测距和测向结果，以及虚拟基线，按三角函数关系可得到左右虚拟站点相对目标的径向距离：

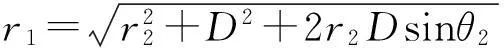
(3)

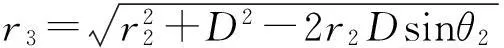
(4)

由虚拟测距结果可得到在2个虚拟站点之间的虚拟程差：

ΔR13=r1-r3。

(5)

或得到实测单站与右侧虚拟站点之间的虚拟程差：

ΔR23=r2-r3。

(6)

根据文献[10]的最新研究结果，对于长基线双站测向可使用如下计算式：

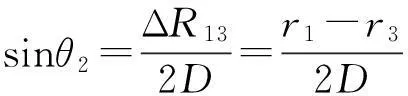
(7)

如仅利用右侧虚拟站点进行虚拟测向，则直接利用短基线近似测向式：

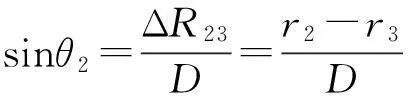
(8)

2误差分析

2.1实测单站测距误差

求解测距式(1)中的各个观测量Δφi的偏微分，对各个相差D的偏微分有如下相乘关系,且为简明起见，式中径向距离的下标已省略：

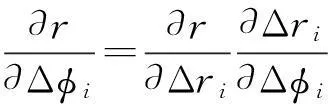
(9)

在假定相位差测量项中所包含的整周数是常数的情况下，Δri项对相差的微分是：

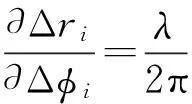
为简洁，式中所包含的相位测量项都用程差Δri等价替代，经求解后有：

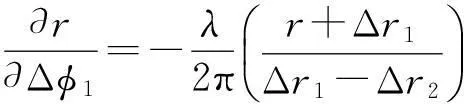
(10)

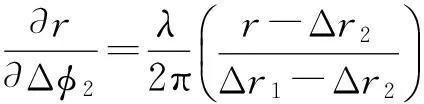
(11)

2.2实测单站测向误差

为分析简单，采用短基线近似测向式，且设方位测量仅与Δφ1相关：

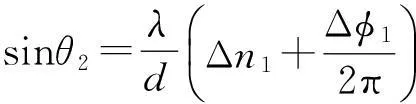
(12)

可求得对方位角的微分为：

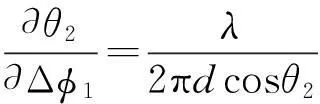
(13)

2.3虚拟站点的测距误差

对于左侧站点，有

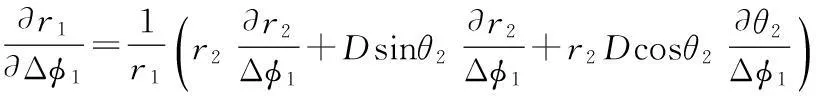
(14)

(15)

对于右侧站点有：

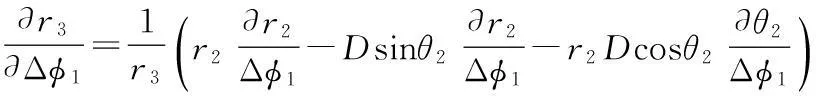
(16)

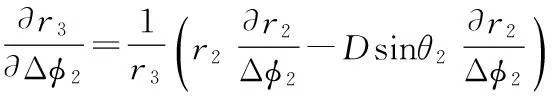
(17)

2.4虚拟双站测向误差

基于实测单站相差测量的虚拟双站测向误差分量为：

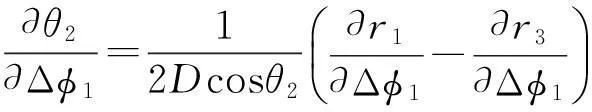
(18)

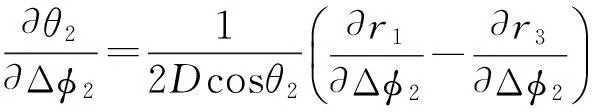
(19)

根据误差测量原理，以度为单位的总的测向误差是：

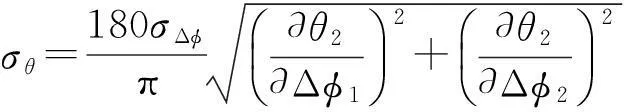
(20)

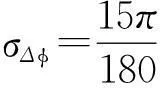
不同虚拟基线时的方位测量误差如图3所示，并和短基线近似测向式的测量误差做了比较。模拟计算表明，当虚拟基线较短时，其测量误差是和短基线近似测向误差基本接近的，当虚拟基线逐渐增加到某个值域时会呈现比单基近似测向更好的测量精度，随后如继续增加虚拟基线的长度，则测量精度开始变劣。 此测量特性并不随目标对实测站点的径向距离以及信号波长的变化而改变。

模拟计算所用的参数：r2=100km，λ=0.15m。

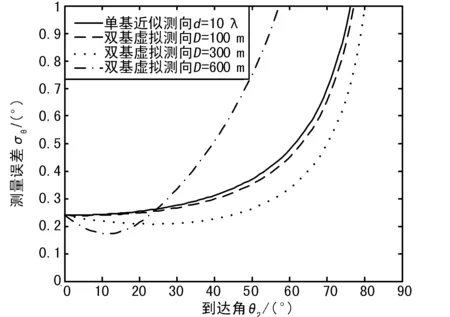
图3　虚拟双站测向误差

2.5虚拟单站测向误差

基于实测单站相差测量的虚拟单站测向误差分量是：

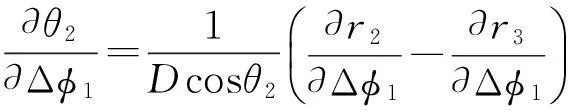
(21)

(22)

仅利一个右侧虚拟站点的虚拟测向误差如图4所示。

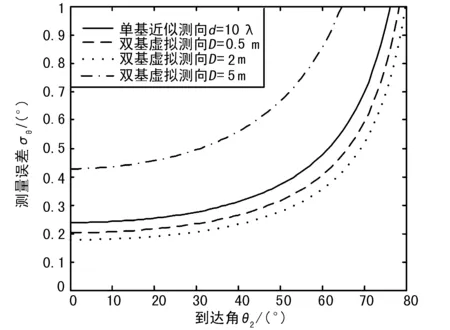
图4　虚拟单站测向误差

其中，误差随虚拟基线长度的变化特性和虚拟双站基本类似，但在整个到达角象限内，其误差曲线基本上是和单基近似测向的误差曲线等距平行的，而虚拟双站在到达角趋于零度时的测量误差是固定不变的。另一个不同特性是所选择的虚拟基线长度仅在几米范围之内，这事实上恰好是和近似短基线测向式的使用条件相吻合的。

3结束语

基于数学模型的分析结果表明，借助虚拟观测拓展基线长度，由此间接通过虚拟程差求解目标方位的方式能提高单站测向精度，但提高的程度似乎还是比较有限的。目前一个可行的用途是均衡在整个探测区域内的测向精度，现有的单基近似测向误差是随到达角的增加而逐渐增大，而利用虚拟双站所得到的测向误差则具有先随到达角下降然后再上升的特性。

仔细观察还可以发现，仅利用一个虚拟观测站能得到更高一些的测向精度，这从数学形式上来说应是合理的。因为，对于多站定位，总的定位误差将是多个不同的、独立的测量参量的误差分量之和，于是多站点的定位误差肯定将比具有较少站点的定位误差更大些。

参考文献

[1]张锡祥,肖开奇,顾杰.新体制雷达对抗导论[M].北京：北京理工大学出版社，2010.

[2]唐永年.雷达对抗工程[M].北京：北京航空航天大学出版社,2012.

[3]左乐，聂剑坤.一种高精度求解入射角的新方法[J].电子信息对抗技术，2014(4): 23-26.

[4]何晓明，赵波，吴琳.基于数字干涉仪的机载ESM系统实现方法及测向误差分析[J].舰船电子对抗,2013,36(6):1-5.

[5]罗贤欣，刘光斌，王忠.干涉仪测向技术研究[J].舰船电子工程，2012(8):74-76.

[6]王志荣.高精度的来波方位估计[J].无线电工程，2007,37(11): 24-25.

[7]杨忠.一种基于干涉仪体制的机载测向技术研究[J].无线电工程，2010,40(12): 58-60.

[8]郁涛.基于基线相似扩展的相差定位技术[J].中国电子科学研究院学报,2012，6(6):650-654.

[9]郁涛.对相似递推程差的一种修正方法[J].现代导航，2014,5(4):288-292.

[10]郁涛.一种长基线高精度时差测向算法[J].无线电工程，2015，45(9)：34-36.

doi:郁涛男，(1957—)，高级工程师。主要研究方向：无源定位。10.3969/j.issn.1003-3106.2016.02.18

作者简介

中图分类号TN97

文献标识码A

文章编号1003-3106(2016)02-0069-03

收稿日期：2015-11-17

引用格式：郁涛.一种借助虚拟观测降低单站测向误差的方法[J].无线电工程,2016,46(2):69-71.