箔条弹RCS测量数据异常值的检验与剔除算法研究

韩 伟, 张鸿喜

(91404部队93分队,秦皇岛 066001)

箔条弹RCS测量数据异常值的检验与剔除算法研究

韩 伟, 张鸿喜

(91404部队93分队,秦皇岛 066001)

传统的异常值剔除方法主要是针对静态测量数据,箔条弹RCS(雷达反射截面积)特性测量属于动态测量,由于动态系统测量中的数据是不断变化的,因此不能沿用静态测量中的数据异常值的剔除方法和判别准则。针对这个问题,提出了利用绝对均值法和基于邻近去最值均值滤波检测方法两种方法,对箔条弹RCS测量数据中的异常值进行剔除,并给出了实际算例。研究结果可为箔条弹RCS测量试验中数据处理及其他动态测量异常数据剔除提供方法借鉴。

动态测量; 异常值; 均值滤波; 雷达截面积

1 引 言

在箔条弹RCS(雷达反射截面积)测量试验过程中,由于各种各样的原因,会出现概率很小但作用强烈的偶发性干扰等,从而产生了异常数据。在数据采集测量过程中,有时会出现一些严重偏离样本集合散布中心(或数据主体趋势)的小部分样本点,即使是高质量的原始采样数据,由于受到多种偶然因素的影响,往往包含有较大的随机误差,在统计学中,将这种测量所得数据称之为异常值,又称野值或者粗大误差。

目前对静态测量数据中的异常值比较容易判别,已有成熟理论。对于动态测量数据异常值剔除方法,当前研究较多的是卡尔曼滤波辨识方法,卡尔曼滤波辨识方法依赖于过去正常的测量值对当前时刻的预报值。但箔条弹布放后形成的箔条云目标比较复杂,再加上海面背景及其自身的闪烁特性,RCS测量数据有快速大动态的起伏属于正常情况。因此卡尔曼滤波法不适合对箔条弹RCS测量数据进行异常值检测。本文对如何判别箔条弹RCS测量数据异常值以及剔除方法进行研究。

2 箔条弹RCS动态测量分析

2.1 动态测量的基本特征

动态测量具有以下四个基本特征:

(1) 时空性。在某些动态测量中,被测量或测量信号随时间而变,动态测量数据也表现为测量时间的函数,即动态测量具有时变性,可用时间参数来描述;而在有些情况下,例如对大多数几何量测量系统,尤其是在数据处理时,用空间参数描述更为方便合理,从这个意义上来说,动态测量具有空间性。因而,动态测量具有时空性。

(2) 随机性。由于在动态测量过程中,难免存在各种外界干扰,因此它是一个高斯或非高斯过程,总表现为时间的随机函数;另外,被测量自身也可能是个随机函数,当测量系统对被测量进行采样时,得到的是若干个随机序列(或随机过程)。因而,动态测量具有随机性。

(3) 相关性。由于测量系统的输出值不仅仅和该时刻的输入值有关,而且和被测量在该时刻以前的量值变化历程有关,必须从所获取测量值的整体数据推估被测量的量值。因而,动态测量具有相关性。

(4) 动态性。在测量过程中,测量系统始终处于运动状态,需要用微分方程(或差分方程)来描述其所输入的含有被测量信息的信号与所输出的动态测量结果之间的关系,或以该系统内部状态变量形成的状态方程来描述,一般常用与之等价的传递函数、时域上的脉冲响应函数或频域上的频率响应函数等来反映该测量系统的动态特性[1]。

2.2 影响箔条弹RCS测量精度的因素分析

箔条弹爆开后形成箔条云的RCS随时间而变,RCS时间特性表现为测量时间的函数,因此箔条弹RCS测量是动态测量。在实际测量过程一般采用相对测量法,即通过与RCS已知的标准球的回波进行比较的方法来得到复杂目标的RCS。这样RCS动态测量的误差来源主要有两部分:一部分是由目标测量过程引入的;另一部分是由对金属球的定标过程引入的。

影响RCS动态测量精度的主要因素有:

(1) 测量雷达的性能

在RCS动态测量中,一方面持续工作时间较长,另一方面,目标回波的信噪比较低,且表现出剧烈的起伏,表现出很大的动态范围。所以RCS动态测量雷达的稳定性、精度、灵敏度、动态范围等都会对测量结果产生重要的影响。

(2) 标准球自身误差

RCS动态测量中用来定标的标准球,在理论上金属球的RCS是各向同性的。但由于机械公差等因索的影响,球的规则性、表面的光度、洁度等方面都会存在一些问题,作为标准体的金属球,其RCS也会随着测量条件的不同同而发生一定的变化,特别是对于较短的波长特别是毫米波照射时,金属球的误差将对被测目标的RCS精度产生很大的影响。

(3) 测距误差

该项误差是由测量系统中的跟踪雷达的测距误差造成的,由于RCS测量采用相对测量法,因此对被测目标的测距误差和对标准球的测距误差都会影响RCS的测量精度。

3 箔条弹RCS异常数据的判别方法

箔条弹RCS测量过程中的异常值混入测量值中必然会影响到对箔条弹RCS特性的分析,如果不把测量数据中的这些异常值进行预先剔除,将会给数据处理带来很大的误差,从而影响对箔条弹战技指标的评定。传统的异常值辨识与剔除方法主要是针对静态测量数据,由于动态系统测量中的数据是不断变化的,所以不能沿用静态测量中的数据异常值的剔除方法和判别准则。而应该按照动态测量系统函数具有连续性的特点,检验动态测量数据的合理性,对数据的取舍作出正确判断。在动态测量中预先对异常值进行分析和剔除,有效地排除了杂波及各种干扰因素对测量的影响,得到的数据才能更科学合理地反映目标的真实特性,保证原始数据的可靠性及其有关计算的准确性。

图1为某型箔条弹RCS时间特性测量曲线,可以看出,测量值中存在异常值,如何从测量值中选出异常值并进行剔除呢？下面给出几种方法。

图1 箔条弹RCS时间特性原始测量曲线Fig.1 Original measurement of chaff bomb time response

3.1 绝对均值法

在动态测量中,运用数据采集设备所获得的信号是离散有限的数字时序信号,可表示为:

(1)

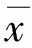
对于零均值数字时序信号则可表示为:

(2)

(3)

其中,n为总的数据长度,k是经验取值系数。

在不同的试验对象和测量系统中k值的确定可通过几次试算来获得,一般地取4-5较为合理[1]。

3.2 基于邻近去最值均值滤波检测

均值滤波算法是基于统计理论的一种能有效抑制噪声的非线性信号处理技术。通常应用于图像处理中的平滑和去噪。其基本原理是对图像中的每个合法像素点邻域中的像素按照灰度级进行排序,然后将该组的均值输出作为该像素点的值。均值滤波定义如下:

(4)

式中,g(x,y)为(x,y)的输出值;f(s,t)为以(x,y)点为中心的邻域内(s,t)点的输入值;Sx,y为以(x,y)点为中心的邻域。邻域类型可以根据研究或应用需要选择方形、一字形、十字形、X形等,邻域大小一般可以选择3×3,5×5。对本文数据类型进行均值滤波,相当于一字形窗口。均值滤波可以消除图像中的椒盐噪声和突变点,但是会改变图像中的原始数据。基于邻近去最值均值滤波是对均值滤波的改进,它对模板S内的数据做了去最值修正处理,即在得到模板S内的数据后,去除了其中的最大最小值(以f(s,t)′表示),再进行均值滤波。该滤波方法极大减小了由于异常点参与运算而导致的滤波结果偏离真值的影响,在不修改原始数据的前提下找出数据中的异常点。因此,本文根据下面的公式给出如下判别规则[2]:

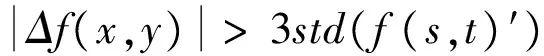
(5)

其中,Δf(x,y)=f(x,y)-mean(f(s,t)′)

式中,f(s,t)′为去除模板内数据的最大最小值的其它数据。若式(5)成立,则(x,y)点为异常点。根据箔条云RCS数据的变化特性,可以采取一滑动检测窗口,对箔条云RCS数据异常值进行检测。具体检测方法为:

(1) 设计一滑动检测窗口,长度为n。

(2) 对窗口内的数据去除最大值和最小值后,求均值及标准差。

4 箔条弹RCS异常数据的判别结果及分析

4.1 绝对均值法判别结果及分析

从图1看出,在箔条云持续时间内,出现了几个数量级为几万的大值,很明显这几个值为异常数据。按照绝对均值法对图1所示的箔条弹RCS数据进行异常数据剔除,结果见图2所示。从图2可以看出,异常数据被有效剔除。

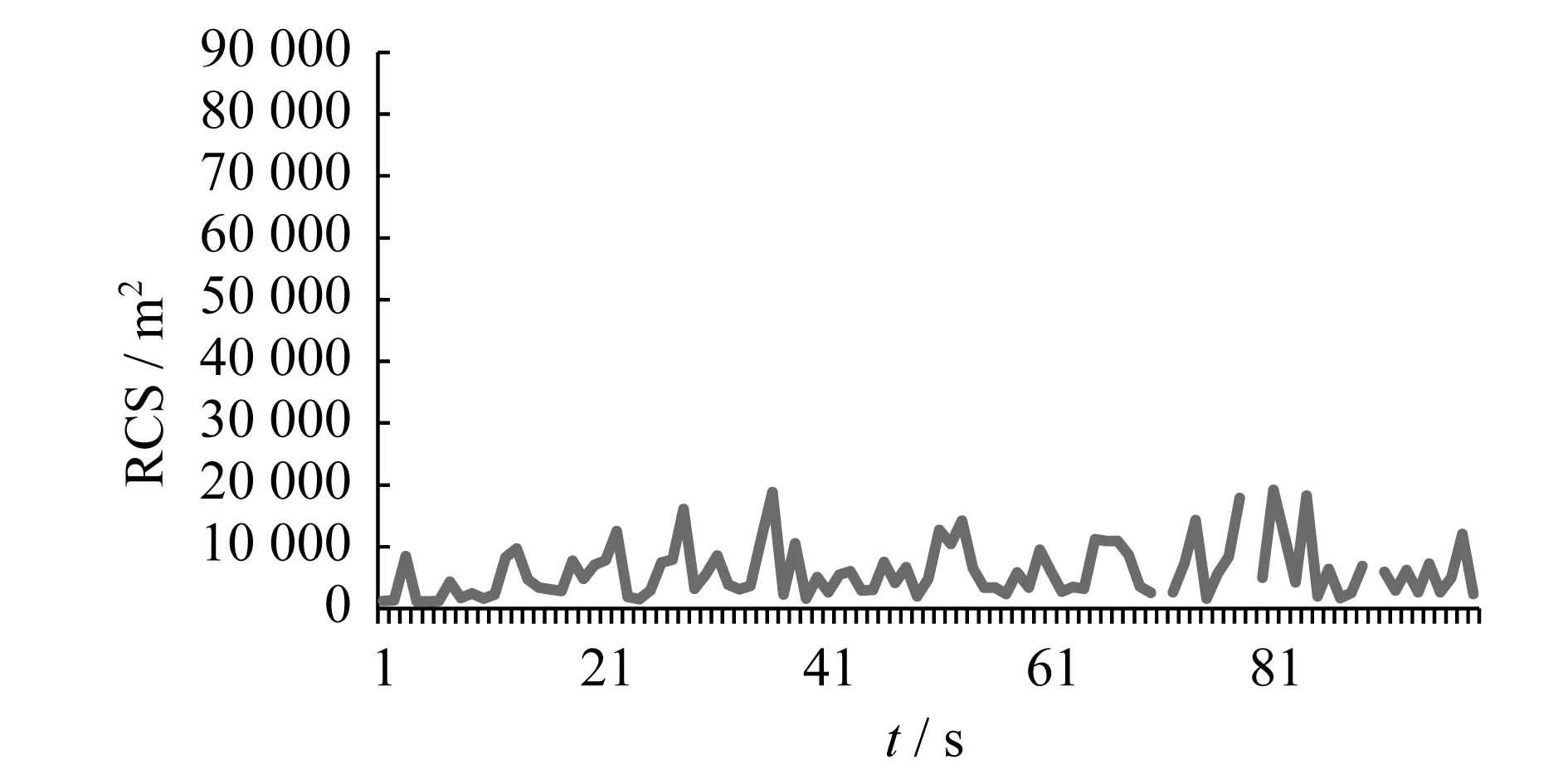
图2 箔条弹RCS时间特性曲线Fig.2 Measurement of chaff bomb time response

4.2 基于邻近去最值均值滤波检测结果及分析

按照基于邻近去最值均值滤波检测方法,设计滑动检测窗口长度为10,对图1的RCS测量数据进行判别,结果如图3所示。

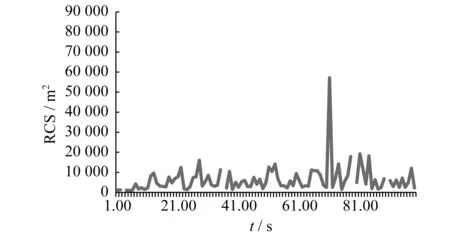
图3 箔条弹RCS时间特性曲线Fig.3 Measurement of chaff bomb time response

由图3可以看出,利用基于邻近去最值均值滤波法剔除异常数据后,仍然存在一明显异常数据,这是因为该方法能够检测出滑动检测窗口内数据中的单个异常跳变,若在滑动窗口内存在多个或连续异常数据,该方法不能剔除全部异常数据。

综上所述,对箔条弹RCS测量数据异常值的判别可以综合使用绝对均值法和基于邻近去最值均值滤波检测方法两种方法,对测量数据中的异常值进行分析和剔除,有效地排除杂波及各种干扰因素对测量的影响,得到能科学合理地反映目标真实散射特性的数据。

5 结 论

在实际工程测量中,测量数据出现异常值的现象是经常发生的。本文对RCS测量雷达测量数据异常值检测问题进行了研究,给出绝对均值法和基于邻近去最值均值滤波检测方法两种方法,对实测数据异常值进行了检测。结果表明,本文算法能够有效剔除数据异常点,是一种有效、可行的箔条弹RCS测量数据异常值检测方法,使测量数据能够真实地反映箔条弹的RCS特性,保证测量数据的可靠性。

[1] 邢靖虹.动态测量数据处理研究[D].西安:西安石油大学,2011.

XING Jinghong.Research on dynamic measurement data processing[D].Xi’an:Xi’an Shiyou University,2011.

[2] 辛欣,周娜,王震.数据异常值检测及修正方法研究[J].现代电子技术,2013,36(11):5-7.

XIN Xin,ZHOU Na,WANG Zhen.Research on data outlier detection and correction method[J].Modern Electronics Technique,2013,36(11):5-7.

[3] 贾沛璋.误差分析与数据处理[M].北京:国防工业出版社,1992.

JIA Peizhang.Errors Analysis and Data Process[M].Beijing:National defense industry press,1992.

[4] 吴石林,张玘.误差分析与数据处理[M].北京:清华大学出版社,2010.

WU Shilin,ZHANG Qi,Errors analysis and data process[M].Beijing:Qinghua university press,2010.

[5] Ronald Kleiss,Achilleas Lazopoulos error in monte carlo,quasi-error in quasi-monte carlo[J].Computer Physics Communications,2005,175(2):93-115.

韩 伟 女(1977-),河北迁西人,高级工程师,主要研究方向为雷达对抗试验及试验数据处理。

张鸿喜 男(1972-),河北秦皇岛人,高级工程师,主要研究方向为电子对抗试验。

OutliersDetection and Removing in RCS MeasurementData of Chaff Bomb

HANWei,ZHANGHongxi

(Unit 93,No.91404 Troops of PLA,Qinhuangdao 066001,China)

Traditional outlier removing method is aiming at static measurement data,measurement of the chaff bomb RCS characteristics is dynamic.Since dynamical measurement data is constantly changing,the outliers detection and removing method for static measurement cannot be adoped anymore.To address this problem,absolute mean value method and the average value filtering method based on the adjacent are proposed to remove the outliers in the chaff bomb RCS data,and some examples are siven.The main results of this study can provide solutions for the the chaff bomb RCS data process and outliers removing of the related dynamical measurement.

dynamical measurement; outliers; average value filtering; radar cross section

TP 391

A