基于改进型遗传算法的PSS系统参数整定及应用

武海南，李 杰

（广东粤电新会发电有限公司，广东 江门 529149）

基于改进型遗传算法的PSS系统参数整定及应用

武海南，李 杰

（广东粤电新会发电有限公司，广东 江门 529149）

在电网大区域联络的背景下，各区域电网的低频振荡问题变得越来越明显。为了保证电网的安全稳定运行，解除低频振荡对联络线传输功率的限制，采用PSS抑制电力系统的低频振荡必不可少。抑制低频振荡的效果主要决定于PSS参数的整定。借用自适应遗传算法对PSS参数整定优化，并以仿真和实际应用验证其正确性，表明取得良好的效果。

PSS；低频振荡；参数整定；遗传算法；自适应

0 引言

电力系统低频振荡的频率范围在0.2～2.5 Hz，对于低频振荡出现的原因，存在着多种解释。其中认可程度最大的当属负阻尼机理，认为电力系统中使用快速、高放大倍数特性的励磁系统调节器，会导致出现负阻尼效果。这种负阻尼会与系统中原有的正阻尼发生中和，从而使得整个电力系统进入了弱阻尼的状态。当系统受到扰动的频率与系统的自然频率存在某种特殊关系时，将会引起功率的增幅或者不衰减的振荡，进而导致系统不能稳定运行[1]。发电机组应用电力系统稳定器（以下简称PSS）是抑制低频振荡的有力措施。

PSS系统的参数整定效果决定了其抑制低频振荡的能力。应用于参数整定的传统方法有继续提升的空间，自适应遗传算法保证群体的多样性，在优化能力上更优。

1 PSS原理

电力系统输送电力的范围大、距离长而且负荷也较重。一旦有干扰因素影响系统，功角出现振荡，此时励磁系统电压调节器提供的附加力矩的相位落后于电网的实际相位，产生了负阻尼，进而使功率振荡更加剧烈。为了消除此种情况，PSS通过引入一个附加的反馈信号，通过提供附加磁链相位上超前功角的相位，使得正阻尼变大，以此削弱低频振荡带来的影响[2]。

目前，PSS的控制算法是以IEEE Std 421.5-2005中PSS2B为基础的。PSS接入信号来源于转速偏差Δω、功率偏差ΔP、频率偏差Δf 3个变量中里的1项或者2项，经过超前、滞后环节来补偿励磁系统中的时滞，产生图1中所示的在Δω轴的附加转矩分量增加系统阻尼，抑制低频振荡[3]。本文中用的NES5100励磁调节器附加的反馈信号为转速偏差Δω、功率偏差ΔP，其数学模型如图2所示[4]，图中T为时间常数，K为放大倍数。

图1 PSS引入向量

图2 NES5100 PSS2B数学模型

根据PSS整定试验导则，PSS输出的转矩相量对应Δω轴在超前10°到滞后 45°，即在-80°～-135°有补偿特性，并使本机振荡频率力矩对应Δω轴角度在0°到滞后30°之间，以产生较大的附加阻尼转矩和较小的附加同步转矩[4]。

当PSS的附加力矩ΔPePSS与Δω同相位，即ΔPePSS只产生的正阻尼正好大于励磁调节器的电磁转矩ΔPe在Δω产生的负阻尼，使励磁调节器提供正阻尼而不产生多余附加分量，在实际中ΔPePSS与Δω同相位是不可能的。当ω变化时，要求ΔPePSS滞后于Δω轴0°到45°即可。

2 PSS参数的自适应遗传算法整定

2.1 自适应算法原理

遗传算法通过模仿生物的遗传、进化机理，进而引用随机统计理论而形成。借助遗传算法中选择、交叉和变异等操作，求解过程是一代代递进式寻找最优解。“适者生存”的核心是淘汰不好的个体，新的一代在各项指标上比上一代好，以此进行下去，一代比一代好。

自适应遗传算法的一般步骤：编码；遗传操作，包括选择、交叉、变异；参数控制；适应函数定标等。具体流程如图3所示。

图3 遗传算法流程

区别于传统遗传算法，自适应遗传算法的交叉率pc和变异率pm要随时调整，其公式为：

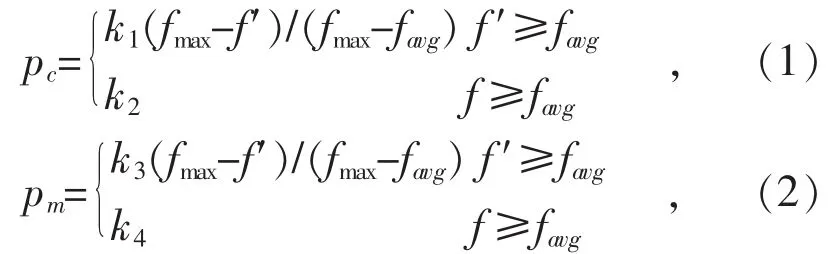
式中：fmax为群体最大适应度值；favg为群体平均适应度值；f′为要交叉的2个个体中最大的适应度值；f为要变异个体的适应度值。

交叉率和变异率随时调整确保了算法的收敛特性，是区别于传统遗传算法的优势所在。

2.2 PSS参数整定

PSS参数整定的过程：根据实测无补偿频率响应特性的测试结果，利用自适应遗传算法进行参数优化，找出多于或等于一组参数，使得不仅能够在低频振荡全部频率范围上出现补偿阻尼，同时也可以对整个系统发挥良性阻尼效果。

通过在线无补偿频率响应特性测试，获得PSS输出和产生阻尼转矩二者之内的全部频率段的相频特性曲线β，如图3所示。某发电机组在满载时，A柜相频特性曲线存在一个低谷，测得凹陷处滞后角为-158.94°，对应频率为1.2 Hz。这是由于机组在本机振荡处阻尼较弱及频率响应测量时相干性等影响造成的，一般可以不考虑这段突变，而将其平滑拉直进行考虑[5]。在0.2～2.0 Hz的低频振荡频段内，测得的滞后角从-15.27°下降到-93.42°。实验预期的理想结果是接入信号通过PSS的滞后角α与β的相互作用产生的相同方向的力矩，也就是制造出一个特定的阻尼转矩。

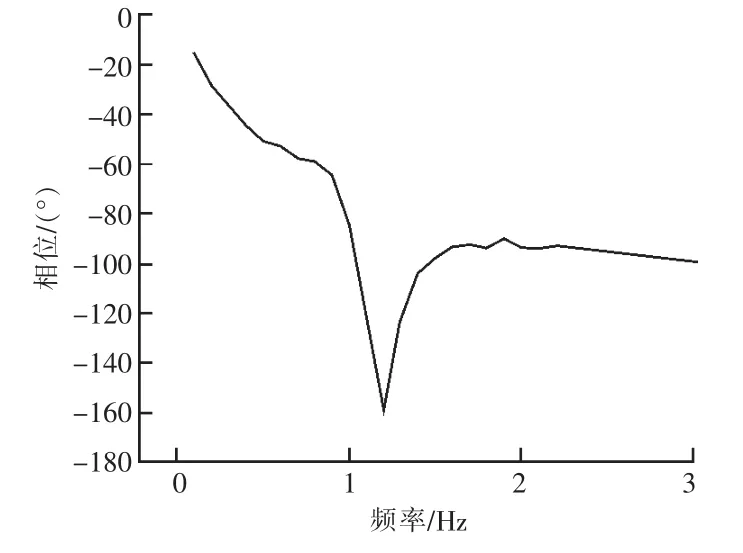
图4 某发电机组满载A柜在线无补偿相频特性

有部分PSS参数必须进行处理，主要包括超前滞后环节T1～T4，它的取值范围0.01～5，增益Ks1值在经过临界增益试验最终确定的。其他参数根据系统推荐设定，隔直环节时间参数Tw1=Tw2= Tw3=4，Tw4=0惯性时间常数T7=4；斜坡时间常数T8=0.2，T9=0.1；放大倍数Ks2=0.5，Ks3=0.5。

参数整定过程如下：

（1）编码、解码。超前滞后过程阶段T1～T4，最小值为Tmin=0.01，最大值为Tmax=5。使用遗传算法将PSS参数进行整定，需要将参数T1～T4进行二进制编码。具体操作为：首先把所有的参数按10位二进制进行编码，相当于把整个取值范围进行1023等分，然后需要对每个分节点进行取值；解码把二进制进行处理，形成对应的实际参数[6]。解码的计算方程式：

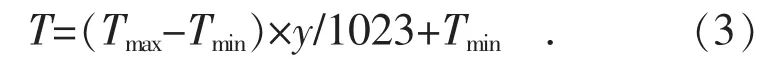
（2）初始种群的产生。遗传算法中最初种群的确定方式是随机的，此处采用MATLAB中的Rand（4×10，个体数）函数产生。

（3）适应度函数设计。遗传算法中最重要的部分是适应度函数，主要作用为锁定预期目标。通过适应度确定达标的优秀群粒子，由于遗传几率的大小与适应程度成正相关的关系，所以只需采用测算群粒子适应度的计算函数就可以对其遗传几率的大小进行评估[7]。在此过程中需要注意前后要保证用同一个原则，并且尽可能筛选出适应性最强的群粒子。群粒子适用度的计算函数要以目标函数为导向，完成筛选过程的重要参考条件。一般情况下，由于T1～T4取值确定，那么弧度s的取值就成为了决定稳定器相频特性值的唯一变量，二者之间的对应关系如式（4）所示：

设函数f（α，β）=α（s）+β（s）-90，设目标函数的表达式如下：

式中：s1至s2为主频率带上对应的弧度值。

式（5）表示的整个频率分布带通过补偿后形成的积分，代表的是相频曲线和Y轴所围成图形的面积。由此可知，设计的目标函数G越小，则通过补偿后出现的附加转矩在低频振荡频率活动范围上越接近方向。

由于适应度函数J与理想预期函数G存在着互为倒数，欲使理想预期函数G取得最小值，需要通过适应度函数的测算筛选出适应程度最高的群粒子。

（4）遗传操作。进行遗传操作的任务是筛选出适应度高群粒子，并且同步把锁定的优秀目标进行交叉和变异，从而达到在全局范围内搜寻优秀目标，在完成这个任务的过程中运用的手段有选择、复制、交叉、变异操作。

（5）参数控制。采用遗传算法最终取得效果的优劣与控制参数确定环节有很大的关联性，确切地说是参数的偏离程度与遗传算法的收敛程度相关联。由此可知，确定控制参数是遗传算法过程中的重要一环，并且群粒子数目越多，得到最优解的可能性更大，也会耗费较长的运行时间[6]。本文选取群体个数80，遗传代数100，变异率根据式（1）确定、交叉率根据式（2）确定。

（6）目标函数。按照之前适应度函数计算方法中提到的，设定的理想预期函数通过补偿后的相频曲线与Y轴所包围面积导出，可以得到s1到s2的频率范围上处于相同位置。在一些频率范围上，它所处位置的高低与频率范围上的任何其它点是有区别的，并且所处位置越高，相角补偿的效果越好。固有PSS单个频率点与整个频率范围参数一致性是预期理想函数的设计依据。为使PSS参数得到最大程度的优化，确定预期理想函数采用了加权方法，预期理想函数如下：

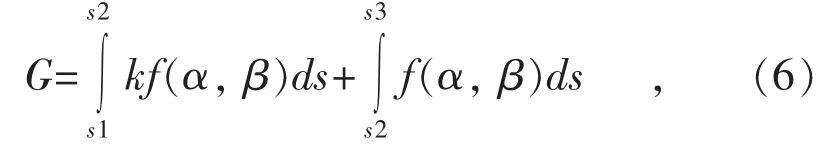
式中：s1到s2表示的是关键频率范围；k表示的是权重值；s1到s3表示的是低频振荡全部频率范围。

将在线无补偿频率响应特性的测试结果与基于自适应遗传算法的机组PSS参数进行综合，获得PSS设计参数见表1。综合过程为：把无补偿频率特性与PSS单元频率响应特性求和，记录求和之后落在0.2～2.0 Hz频率范围的相位滞后结果，并且要确保PSS输出的力矩向量所对应Δω轴在超前10°至滞后45°范围内，同时也必须满足本机振荡频率力矩对应Δω轴在0°至滞后30°范围内[8]。

表1 某机组PSS设计参数

计算得到满载时励磁调节器A柜投入PSS参数时的有补偿相频特性图5所示。

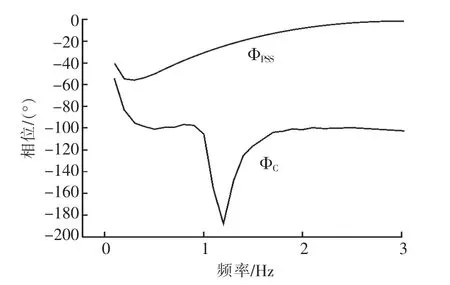
图5 某发电机组满载A柜有补偿相频特性

由图5可知，某发电机组满载PSS参数投入A柜时，在0.2～2.0 Hz的频段内有补偿频率响应的相频特性低频段得到了滞后补偿，在0.2～2.0 Hz的整个频段范围内PSS相位补偿均满足国标的要求[9]。

3 仿真分析验证

3.1 系统参数

结合实际情况及研究需要，以4机2区域系统为仿真对象，2区域联系弱，电力系统容易失去稳定。2区域对称且4台发电机、变压器参数相同。具体参数如表2、表3所示。

表2 发电机变压器主要参数

通过特征值分析，选取最弱阻尼振荡，阻尼比为0.8265%。整定PSS参数后，传统PSS整定阻尼比为7.6%，优化后PSS整定阻尼比为10.3%。

放大倍数KS1值一般取临界增益的1/5～1/3。按照PSS模型的本机振荡频率的模值及PSS的阻尼效果考虑，取KS1=12。

以2%阶跃量作为扰动时，传统遗传算法得到PSS参数加入时，发电机转速偏差，即频率偏差如图6所示。

由图6可知，附加PSS后，振荡得到抑制，大约4 s后基本稳定，但是不太理想。

同样扰动时，自适应遗传算法得到PSS参数加入时，发电机转速偏差如图7所示。

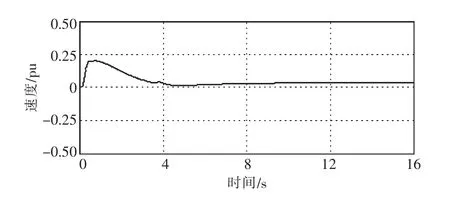
图6 传统遗传算法附加PSS时发电机转速偏差

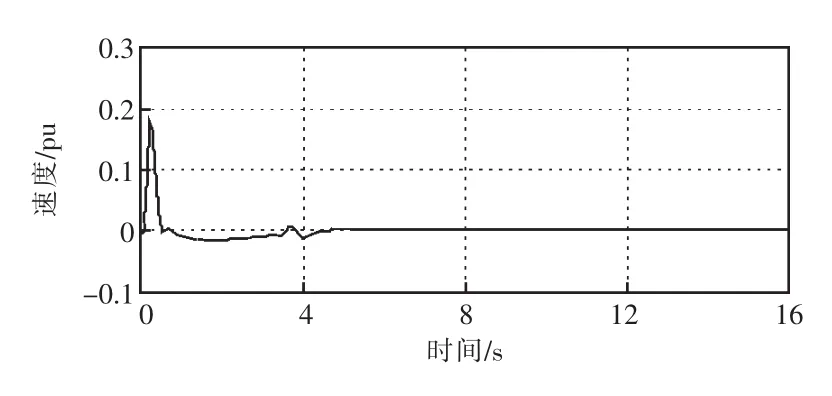
图7 自适应遗传算法附加PSS时发电机转速偏差

由图7可知，自适应算法优化PSS参数后，系统正阻尼良好，1 s左右趋于稳定，振荡幅度明显变小，抑制振荡效果很好。

3.2 试验验证

试验在满载的条件下进行，不投入PSS补偿时逐步增大扰动量，有功功率波动的峰峰值达到30 MW左右或振荡次数大于5，对应的电压扰动量为此次扰动试验的阶跃量，最终选定±1.5%阶跃量。

励磁调节器±1.5%阶跃满载无PSS时的扰动情况如图8所示，从图中可以看到，有功功率峰峰值达到16.78 MW，约为额定有功功率的4.8%。

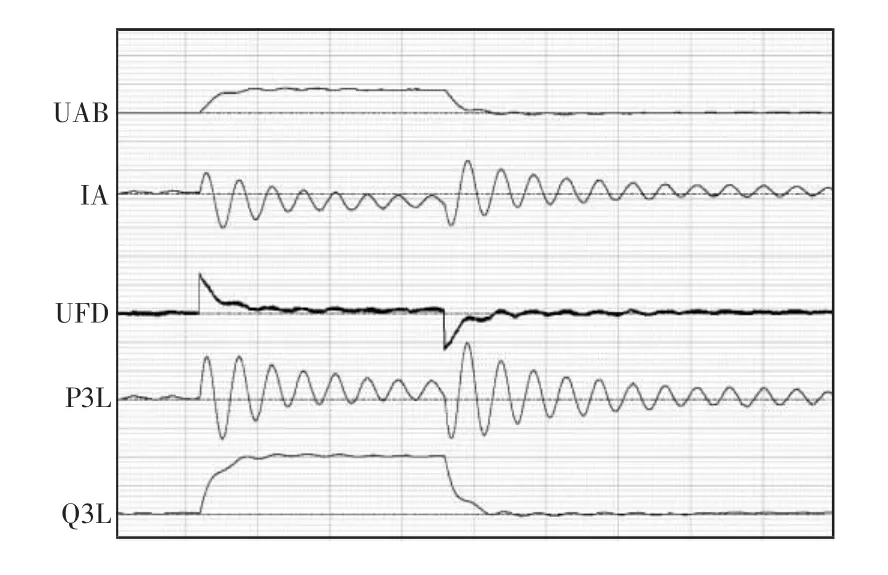
图8 无PSS满载时±1.5%阶跃

如图9、图10所示，输入整定参数投入PSS进行满载±1.5%阶跃试验，传统PSS参数下测得的有功功率峰峰值为13.31 MW，遗传算法PSS参数下测得的有功功率峰峰值为8.77 MW，振荡均持续时间上遗传算法PSS参数下收敛较快，曲线的平滑性更好。其参数对于本机振荡频率1.1 Hz左右的有功振荡有良好抑制效果，证明遗传算法优化整定参数的正确性[9-10]，同时满足在0.2～ 2 Hz较宽频段内的补偿要求。

图9 传统方法PSS参数投入满载时±1.5%阶跃

图10 遗传算法PSS参数投入满载时±1.5%阶跃

励磁调节器±1.5%阶跃60%负载无PSS时的扰动情况如图11所示，从图中可以看到，有功功率峰峰值达到10.73 MW，约为有功功率的5.1%。

图11 无PSS60%负载时±1.5%阶跃

同样在投入遗传算法整定PSS后进行阶跃试验，试验结果如图12所示，有功功率均振荡仅持续了1周就收敛，有功功率波动的最大峰峰值降为4.63 MW，约为额定有功的2.2%，抑制效果明显。

图12 PSS参数投入60%负载时±1.5%阶跃

4 结论

提出自适应遗传算法应用于PSS参数整定，通过仿真及试验，证明其有较好的收敛特性。相比传统的PSS参数整定方法，经过自适应遗传算法优化后的参数在主振荡频率点和全频带的阻尼效果更好，同时，对振荡的抑制能力更强，纹波更少，线形更加平滑。

[1]竺士章．发电机励磁系统试验[M].北京：中国电力出版社，2005:13-15．

[2]吴跨宇，竺士章．发电机励磁系统调差对PSS参数整定的影响与对策[J].电力自动化设备，2010，25（9）：10-15．

[3]南京南瑞集团公司电气控制分公司．南瑞NES5100励磁调节器用户手册[Z].南京：南瑞，2008.

[4]DL/T 1231-2013电力系统稳定器整定试验导则[S].北京：国家能源局，2013.

[5]翁洪杰．电力系统稳定器现场整定试验中若干问题探讨[J].广东电力，2010，25（9）:10-15．

[6]苏琳.基于改进遗传算法的电力系统无功优化[D].成都：西南交通大学，2006.

[7]F P DE MELLO.Concepts of synchronous machine stability as affected byexcitation control[J].IEEE Transactions on Power Apparatus and Systems，2008，88（4）:316-329.

[8]向宝录，刘冠环．电力系统稳定器（PSS）整定试验过程中机组跳闸的探讨[J].电力系统保护与控制，2010，25（9）:10-15．

[9]曾艳，陈迅．基于PSD程序的PSS参数优化设计、现场整定试验及仿真校核计算[J].电力自动化设备，2009，25（9）:10-15．

[10]严伟佳．电力系统低频振荡阻尼控制研究[D].南京：东南大学，2006.

（本文编辑：杨 勇）

Parameter Setting of PSS Based on Improved Genetic Algorithm and the Application

WU Hainan，LI Jie
（Guangdong Yuedian Xinhui Power Generation Co.，Ltd.，Jiangmen Guangdong 529149，China）

In the context of power grid connection in large areas，low-frequency oscillation in regional power grids is becoming more and more obvious.In order to ensure operation safety and stability of power grid and eliminate limit of low-voltage frequency oscillation to transmission power of tie line，power system stabilizer（PSS）is necessary to inhibit the low-frequency oscillation in electric power system.The effect of low-frequency oscillation inhibition mainly depends on the quality of PSS parameter setting.Adaptive genetic algorithm is adopted to optimize PSS parameter setting，and the simulation and practical application are used to verify the correctness of the method，which turns out to be effective.

PSS；low-frequency oscillation；parameters setting；genetic algorithm；adaptive

TM731

B

1007-1881（2016）06-0011-06

2016-03-04

武海南（1987），男，工学硕士，从事发电厂调试以及运行相关工作。