基于模态贡献度系数的大跨度桥梁抖振响应分析

邹孔庆，黄文锋，王美芹，周焕林（合肥工业大学土木与水利工程学院，安徽合肥　230009）



基于模态贡献度系数的大跨度桥梁抖振响应分析

邹孔庆，黄文锋，王美芹，周焕林
（合肥工业大学土木与水利工程学院，安徽合肥230009）

摘要：文章基于结构动力响应分析及模态分析理论，推导了大跨度桥梁模态贡献度系数和最优时间步长计算公式，并编写相应的计算程序。针对普立特悬索桥的结构特点，计算分析其模态贡献度系数及相应的优化时间步长Δt，再将其引入普立特悬索桥在风荷载作用下的抖振时域响应分析。计算结果表明，采用优化时间步长Δt＝0.05计算得到的各方向抖振响应均沿平衡位置上下波动，顺风向比垂直向位移响应大4倍左右。通过对比分析可知，采用优化的时间步长使计算结果在精度和效率上得到很好的保证，为普立特悬索桥的抗风分析提供了依据，可供同类结构精细化的动力分析做参考。

关键词：模态贡献度系数；优化时间步长；大跨度桥梁；抖振响应

周焕林（1973-），男，安徽宿松人，博士，合肥工业大学教授，博士生导师.

0　引　言

大跨度悬索桥为几何形态比较复杂的空间结构受力体系［1］，理论上，该类结构具有无限多的自由度，因而具有无限多个模态，且各模态间存在耦连性。通常结构动力分析中只取对结构响应贡献度较大的有限个模态进行计算，但却很难准确地确定临界点频率位置，从而难以确定在响应计算中所参与的模态数。如果在计算中仅考虑较低阶模态，会引发高阶模态响应的丢失问题，导致计算结果出现偏差并影响整体和局部响应效果，若考虑太多的高阶模态参与计算，使计算过程更加耗时和占用更多内存。因此，合理准确地确定参与模态数及相应的临界频率是十分重要的，同时建立该临界频率与结构动力分析的联系是要解决的关键问题之一。

对大跨度桥梁结构的动力响应分析，常采用模态分析法和逐步积分法。前者采用了叠加原理，故只能适用于线性系统中，但是后者适用于分析任何体系结构以及其非线性动力响应问题。目前，大跨度桥梁结构动力分析更侧重于研究结构的各种非线性行为，特别是分析在随机且变化规律复杂的风荷载作用下结构动力响应的非线性问题，故采用逐步积分法求解更加合适。

但该方法的计算精度与时间步长关联密切，并且由于低通滤波的作用，如果时间步长太大将会过滤掉高阶频率对结构响应的贡献，如果时间步长太小将使计算过程耗时和占用内存，因而需要确定最合理的时间步长。其值本身的确定不涉及结构振型和频率，但可根据结构临界频率确定，从而可建立临界频率和动力分析的关系。而该临界频率可通过各阶模态的贡献度系数分析得到，最终使得结构计算结果在精度和效率上均得到有效保障。

本文在结构动力学及模态分析理论基础上，推导得到桥梁结构模态贡献度系数和最优时间步长的计算公式，并编写了相应的计算程序，再结合普立特悬索桥模态分析结果计算得到该桥梁的各阶模态贡献度系数，将确定的最优时间步长应用到该桥中，并利用逐步积分法进行风荷载作用下桥梁时域内的抖振响应计算分析，对采用不同时间步长的抖振响应计算结果进行了对比分析与讨论。

1　模态柔度矩阵

桥梁结构线性n维多自由度系统受迫振动的动力学方程表达式为：

其中，K、C、M分别为桥梁的n×n阶等效刚度、阻尼和质量矩阵；δ（t）、.δ（t）、¨δ（t）分别为桥梁响应的n维位移、速度和加速度列向量；P（t）为桥梁结构n维激振力矩阵。

对（1）式进行拉普拉斯变换，假设初始的位移、速度及加速度均为0，可得：

相应地，系统的传递函数为：

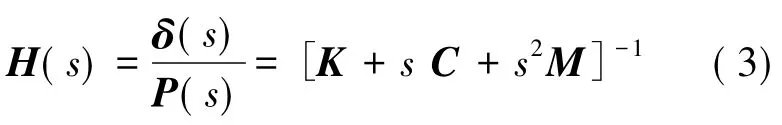
当s＝jω时，（3）式可转化［2］为：

进一步，令ω＝0，则（4）式变为：

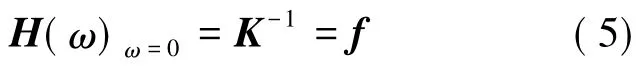
根据模态分析理论，（3）式可表示为：

其中，Φi为第i阶模态向量；λi为第i阶模态特征值，λi＝ω2

i；ω为圆频率；N为结构总模态数；Mi为第i阶模态的模态质量比例系数；*为变量的复共轭对。

从理论上讲，对于有限个模态数，传递函数满足收敛条件。因此，由（5）式、（6）式可得结构的柔度矩阵为：

由于桥梁结构动力特性分析中参与的模态一般为实数值，结构柔度矩阵可表示为：

其中，MAi为比例系数，可根据结构有限元模型计算获取。一般来说，当前N阶结构模态对结构柔度的贡献度大于一定比例（如95%）时，即可较好地逼近结构的真正柔度。

从而可得单位荷载向量作用下结构位移响应的表达式为：

其中，F为施加于柔度矩阵f的单位荷载向量。

2　模态贡献度系数及最优时间步长的确定

桥梁结构贡献度系数为单个模态引起的结构位移所占结构总位移的比重，反映了结构各模态行为对总体动力行为的贡献。即单个模态贡献行为越大，其对结构整体振动的贡献度越大，反之越小。从而，结构第j阶模态的模态贡献度系数［3］可定义为：

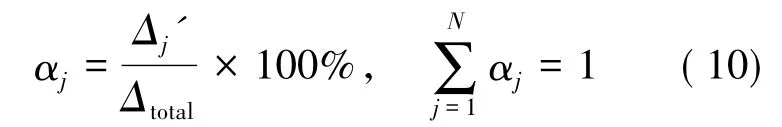
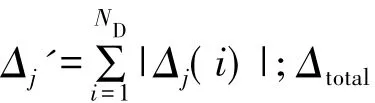
根据结构动力响应分析的逐步积分法，可确定进行结构响应分析所需的最优化时间步长Δt为：

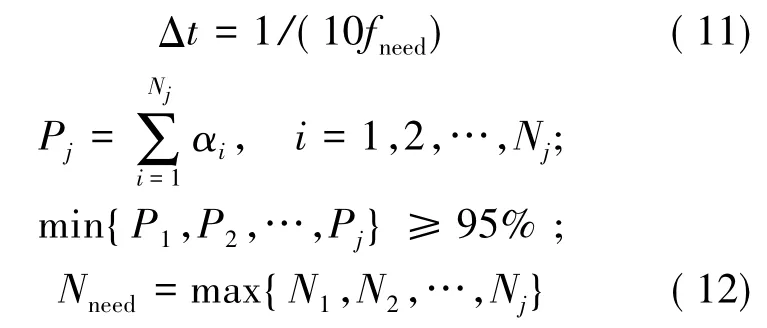
因此，将（10）式代入（11）式、（12）式可以得到当Δt取10倍最高界限频率的倒数时所对应的最优化时间步长，从而可保证得到比较合理的结构响应计算精度和效率。

3　普立特悬索桥模态分析

利用有限元分析软件ANSYS建立了云南普立特悬索桥的三维结构有限元模型，主要由主缆、吊索、主塔、加劲主梁及桥墩等组成，其空间有限元模型如图1所示。整个模型共有908个节点、869个单元，其中主缆单元164个、吊索单元102个、主塔和桥墩单元336个、主梁单元152个，其他均为质量元。

图1　全桥有限元模型

主梁采用空间鱼刺模型，刚性鱼骨刺横梁和主塔通过主缆连接横梁。主缆和吊索采用link8单元模拟，主塔和桥墩采用beam4单元模拟，加劲主梁采用beam4单元模拟，主梁与主塔的连接采用弹簧-阻尼单元combin14和mass21，该全桥空间有限元模型如图1所示。全桥所采用的边界条件为：两桥塔底部完全固结、主缆在两侧锚定固结、塔顶固结。

对于大跨度悬索桥而言，自重刚度是由恒载作用所产生的主缆初始应力所提供的。故在计算普立特悬索桥动力特性时，先计算恒载作用下的非线性静力响应［4］，验证结构处于平衡状态时的几何位置是否合理，并为模态分析计算提供最终的结构刚度。然后在此基础上进行桥梁结构模态分析，得到普立特悬索桥前10阶自振频率及振型见表1所列。

普立特悬索桥的基本周期为8 s左右，表现为主梁侧向漂移和反对称竖弯，频率主要分布在0.12～1 Hz内，其分布较为密集，同时桥塔振动为主的振型出现较晚，如桥塔反对称侧弯发生在0.84 Hz的第31阶，故桥梁结构动力特性主要表现在前几阶振型。

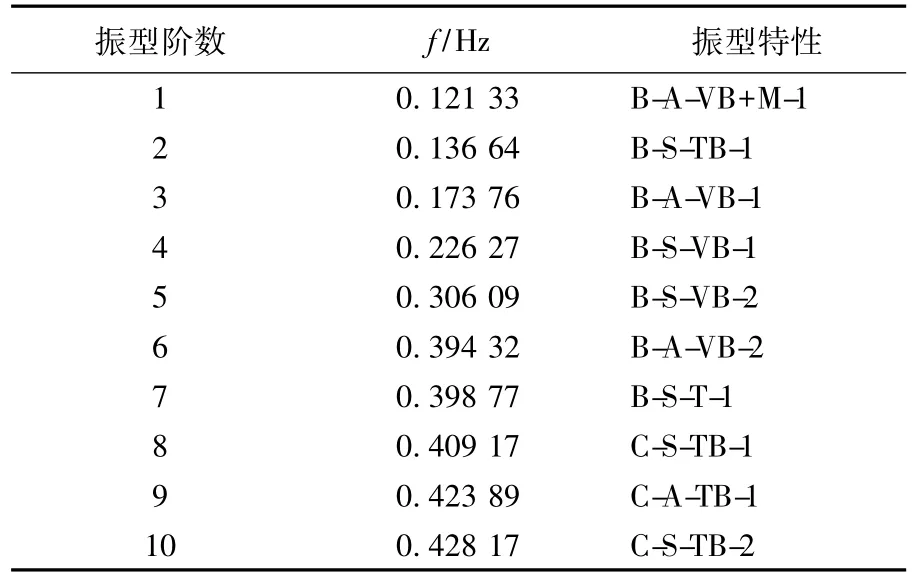
表1　悬索桥自振频率及振型特性

4　普立特悬索桥全桥体系贡献度系数分析

该桥柔度贡献度大于95%所需的模态总数以及总贡献度见表2所列。

表2　模态总数及其总贡献度

从表2可看出，前60阶模态可很好地反映该桥主梁竖向挠曲和扭转以及塔墩横向挠曲、纵向挠曲振动特性，而主梁横向挠曲振动需要考虑到74阶模态。该桥主梁竖、横向挠曲和扭转模态贡献度系数分布如图2所示。

从图2可知，该桥主梁竖弯挠曲刚度集中分布于少数几阶的振动模态中，而主梁横向挠曲、扭转刚度则离散分布于多阶振动模态中。

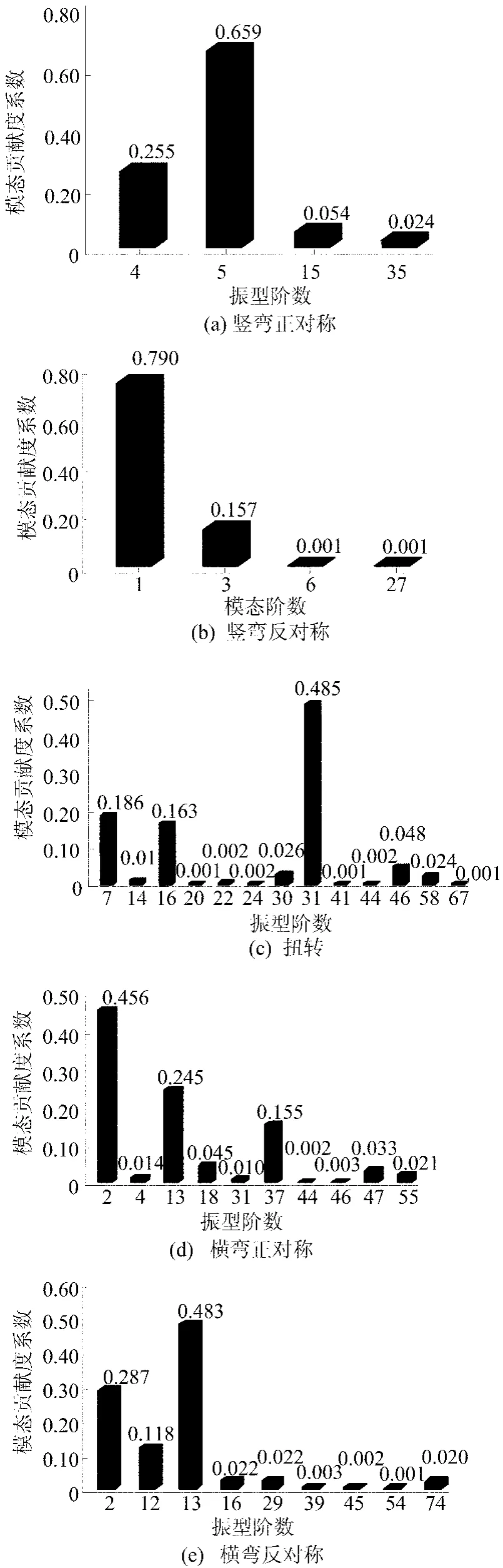
图2　主梁体系模态贡献度系数

5　桥梁结构的响应分析

采用Deodatis的谐波合成法模拟云南普立特大桥处的空间脉动风场［5］，脉动风速时程模拟及检验结果如图3、图4所示。

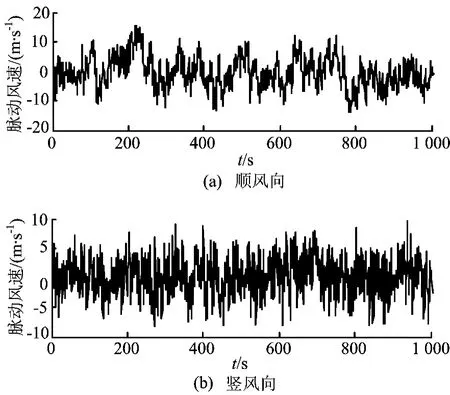
图3　主梁跨中点模拟顺风向、竖风向风速时程

图4　主梁跨中点竖风向脉动模拟结果检验

采用基于准定常理论的抖振力计算公式［6］，将风速时程转化为作用于桥梁上的等效抖振力时程，该过程在Matlab软件中实现了生成数据文本，并考虑了节点的等效迎风面积。再利用ANSYS的APDL进行二次开发即可实现循环加载［7］。计算所采用的主梁气动分力系数由节段模型风洞实验得出，结果如图5所示。

结构的自激力分析采用ANSYS自带MATRIX27单元输入其气动刚度矩阵和气动阻尼矩阵的参数实现［6］，各参数表达式见文献［8］。在计算中应分别考虑-12°～12°共25种工况，本文仅对0°工况进行分析。结构阻尼系数根据近似Raileigh阻尼模型公式并结合模态分析计算可得：α＝0.000 93，β＝0.019 23。

图5　普立特悬索桥气动三分力系数

将得到的抖振力时程施加于该桥的有限元模型上，并考虑自激力的影响，编写其相应的循环加载批量数据和结果后处理程序，计算时间取1 000 s，得到该桥梁的抖振响应如图6所示。

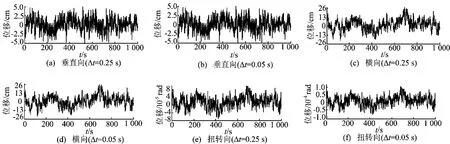
图6　不同时间步长下主梁跨中点抖振位移时程响应

计算过程中考虑结构的几何非线性因素，对云南普立特大桥而言，几何非线性的影响因素主要来源于缆索的垂度效应、结构初应力和结构大变形。本文采取的措施是在ANSYS中打开几何大变形开关（nlgeon，on）、应力刚化（stess stiffening）及更变坐标（upcood，1，on）。动力响应采用Newmark逐步积分方法对该结构进行抖振时域分析，根据上述理论推导出该桥梁结构最优化时间步长为0.05 s，本文设置积分时间步长分别为0.25、0.05 s，此时的结构抖振时域分析结果如图6所示。

由图6可以看出，主梁跨中节点的顺风向、垂直向以及扭转向位移均沿平衡位置上下波动，顺风向位移响应比垂直向位移响应大4倍左右。在采取不同的时间步长进行积分计算后可知，在垂直向位移响应中两者计算的结果相差不大，这是由于振动模态在该方向的贡献度主要集中在前几阶。在顺风向位移响应中0.05 s比0.25 s小5%左右，这与在该方向振动模态的贡献度分布于较多的阶数有关。

而在扭转向位移响应中，后者比前者大15%左右，这是由于扭转方向上振动模态贡献度系数较大的模态阶数主要分布在较高阶频率中。虽然从响应计算结果来看，两者均能很好地描述结构的整体变形，但要更加精确地分析局部构件变形的性质，高频成分就不可忽略。

6　结　论

本文针对普立特悬索桥的结构特点，研究了该桥模态贡献度系数的问题，并利用逐步积分法的Newmark-β方法进行了随机脉动风作用下结构的抖振响应计算时域分析，得到如下结论：

（1）结构模态贡献度系数可综合反映结构各模态刚度对总体贡献度的大小。从贡献度系数分布中可得各振动模态分布的疏密程度，主梁竖弯挠曲刚度集中分布于少数几阶的振动模态中，而主梁横向挠曲、扭转刚度则分布于多阶振动模态中。

（2）利用逐步积分法确定桥梁结构抖振响应，采用最优化方法确定了其最优时间步长为0.05 s。同时考虑了2种不同时间步长下计算得到的抖振响应的差异，证明了采取最优时间步长对结构的分析与计算是十分必要的，可为其他结构动力响应的准确计算提供参考。

（3）普立特悬索桥抖振响应计算结果表明，该桥主梁跨中节点的顺风向、垂直向以及扭转向位移均沿平衡位置上下波动，其中，顺风向位移响应比垂直向位移响应大4倍左右，扭转向的位移响应很弱。

［参考文献］

［1］曾广武，汪本媛，韩振勇.悬索桥主缆初张力对成桥结构性能的影响［J］.中国铁道科学，2007，28（1）：28-32.

［2］曹树谦，张文德，萧龙翔.振动结构模态分析：理论、实验与应用［M］.天津：天津大学出版社，2001：130-197.

［3］马坤全，潘湘文，沈钱斌.空间缆索自锚式悬索桥模态贡献度系数分析［J］.桥梁建设，2009（1）：11-14.

［4］逄焕平，王建国，李雪峰.基于挠度理论的悬索桥静力分析［J］.合肥工业大学学报：自然科学版，2010，33（2）：261-265.

［5］Deodatis G.Simulation of ergodic multivariate stochastic processes［J］.Journal of Engineering Mechanics，1996，122（8）：778 -787.

［6］Sarkar P P，Jones N P，Scanlan R H.Identification of aeroelastic parameters of flexible bridge［J］.Journal of Engineering Mechanics，1994，120（8）：1718-1741.

［7］ANSYS Inc.Theory reference＆ANSYS APDL programmer’s guide［EB/OL］.［2014-10-20］.http：//www.ansys.com.cn.

［8］曾宪武，韩大建.大跨度桥梁风致抖振时域分析及在Ansys中的实现［J］.桥梁建设，2004（1）：9-12.

（责任编辑闫杏丽）

Time domain analysis of buffeting response of long-span bridge based on modal contribution coefficients

ZOU Kong-qing，HUANG Wen-feng，WANG Mei-qin，ZHOU Huan-lin
（School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei 230009，China）

Abstract：Based on the structural dynamics analysis method and modal analysis theory，the modal contribution coefficients and optimal time step for long-span bridge are derived.For Pulite Bridge，the modal contribution coefficients and optimal time step Δt of this bridge are first obtained based on its structural characteristics.Then the buffeting response of this bridge under wind loading in time domain is further calculated by using them.The results show that when optimal time step Δt equals to 0.05，the buffeting response of this bridge varies around equilibrium position for each direction，and the buffeting response in along wind direction is about four times larger than that in vertical direction.Through the comparison with other time step，it can be known that the calculation with optimal time step Δt can give good results in accuracy and efficiency.This research can provide a basic reference for the delicate wind-resistant analysis of Pulite Bridge and other similar bridges.

Key words：modal contribution coefficient；optimal time step；long-span bridge；buffeting response

作者简介：邹孔庆（1990-），男，安徽亳州人，合肥工业大学硕士生；

基金项目：国家自然科学青年基金资助项目（51408174）；安徽省自然科学青年基金资助项目（1408085QE95）；中国博士后科学基金第54批面上资助项目（2013M540511）和中央高校基本科研业务费专项资金资助项目（2013HGBH0037）

收稿日期：2014-12-01；修回日期：2015-02-02

doi：10.3969/j.issn.1003-5060.2016.01.023

中图分类号：U448.25

文献标识码：A

文章编号：1003-5060（2016）01-0122-06