Pω增强型k－ω湍流模型在三角翼旋涡流动的应用

张冬云，李喜乐，杨 永，张 强

（1.中国商用飞机有限责任公司上海飞机设计研究院，上海 201210；2.中国航天空气动力技术研究院，北京 100074；3.西北工业大学翼型、叶栅空气动力学国家重点实验室，陕西西安 710072）

Pω增强型k－ω湍流模型在三角翼旋涡流动的应用

张冬云1，李喜乐2，＊，杨 永3，张 强3

（1.中国商用飞机有限责任公司上海飞机设计研究院，上海 201210；2.中国航天空气动力技术研究院，北京 100074；3.西北工业大学翼型、叶栅空气动力学国家重点实验室，陕西西安 710072）

在三角翼旋涡绕流数值模拟中，标准Wilcoxk－ω湍流模型生成项未考虑旋度的影响而导致预测的旋涡强度较弱。通过引入探测因子区分剪切层和涡核，在旋涡流动的高旋度区域增加ω方程生成项的方法，基于结构化网格上的RANS求解器，加入了Pω增强型k－ω湍流模型，对绕尖前缘三角翼亚声速和跨声速旋涡流场进行了数值模拟。计算结果与NASA的NTF风洞和DLR的DNW－TWG风洞试验数据进行了对比分析，结果表明：不论在亚声速还是跨声速自由来流条件下，Pω增强型k－ω湍流模型计算的压力分布、涡破裂位置均与试验数据吻合良好，准确地预测出了三角翼上翼面的主涡、二次涡结构，特别是跨声速条件下激波干扰导致的涡破裂的临界迎角及涡破裂位置，表明Pω增强型k－ω湍流模型在绕三角翼旋涡流动数值模拟中具有良好的适用性。

k－ω湍流模型；生成项；三角翼；跨声速；临界迎角；涡破裂

0 引 言

现代先进战斗机常采用三角翼布局，绕三角翼大迎角旋涡流动包含复杂的流动现象［1］，它们对战斗机的空气动力特性、操纵性与稳定性、气动弹性和结构动力学特性均会产生重要的影响［2］。因此，近些年科研人员对绕三角翼旋涡流场进行了大量的实验［3－8］和数值模拟［9－14］研究。研究表明在大迎角下，尖前缘三角翼上翼面的旋涡流场包含主分离涡、二次涡，甚至三次涡［15］。随着迎角的增加，分离涡会发生涡破裂现象。亚声速情况下，涡破裂位置随迎角增加逐渐从三角翼后缘向上游移动［16－17］；与亚声速涡破裂现象不同的是，跨声速条件下，由于激波对主涡的干扰作用，在某一临界迎角下，三角翼上会发生涡破裂位置突然前移的现象，使得绕三角翼的跨声速旋涡流动变得更为复杂［11－12，14］。

三角翼上翼面涡破裂的发生与分离涡的许多参数有关（例如基于临界态理论和旋涡稳定性理论的罗斯比数［18－19］，旋转速度、轴向速度和逆压梯度等内部参数的关系等）。因此，在数值模拟研究中，为了准确预测绕三角翼旋涡流动中的涡破裂现象，必须准确预测出分离涡结构。在基于求解RANS方程的三角翼旋涡绕流数值模拟研究中，湍流模型在对涡结构的捕捉中发挥着至关重要的作用，进而影响着对涡破裂的预测。标准的一方程和两方程湍流模型都存在在涡核区域预测的湍流黏性水平过高的问题，导致分离涡较弱，耗散过快，难以准确预测出分离涡结构和涡破裂现象。本文采用Brandsma等［2］提出的方法，在流动的高旋度区域增加ω（耗散率）方程生成项，在基于结构化网格的RANS方程求解器上，加入Pω增强型k－ω湍流模型，对65°后掠角尖前缘三角翼的亚声速和跨声速旋涡流场进行了数值模拟。计算了不同状态下三角翼上翼面的物面压力分布、涡破裂位置，分析了流场结构，通过与试验数据和标准Wilcoxk－ω湍流模型［20］计算结果对比分析，考核了Pω增强型k－ω湍流模型对绕三角翼旋涡流动的数值模拟能力。

1 数值模拟方法

1.1流体力学控制方程

绕三角翼旋涡流场的流动控制方程采用RANS方程，其积分形式为：

其中，V为控制体体积，Q为守恒变量矢量，σ为控制体表面，F为通过表面σ的净通量矢量，包含黏性项和无黏项，n为表面σ的单位外法向矢量。

流动控制方程空间离散采用二阶有限体积方法。无黏通量项的离散采用迎风型通量差分分裂格式（Flux－Difference Splitting）；而对于黏性项，采用二阶中心格式进行离散。定常计算的时间推进采用隐式近似因子化法（Approximate Factorization Method），在每个空间方向上独立进行隐式求解运算。

1.2 标准Wilcoxk－ω湍流模型及其改进

首先，应变率张量和旋转张量分别定义为：

一般情况下，在剪切层内，速度梯度主要为物面法向方向上的梯度，因此，应变率张量和旋转张量大致相等。但是，在接近涡核的区域，流动基本处于旋转状态，旋转张量将会增大。

式（4）从数学上表示了能量从平均流动到脉动速度流场的传递关系，这是由于在涡团拉伸过程中，平均速度梯度和雷诺应力相互作用引起的。其中，只有速度梯度的对称分量（即应变率张量珚Sij）和雷诺应力张量的各向异性分量aij对湍动能有贡献。因此，式（4）可以写为：

可以看出，湍动能的产生与应变率张量是成比例的。对于三角翼旋涡流动，式（5）表明湍流大多出现在剪切层和其周围的流场，不会出现在高速旋转的涡核区域。因此，可以认为涡核区域的湍流度较低，甚至可以认为是层流。

标准Wilcoxk－ω湍流模型是Wilcox［20］基于Boussinesq假设提出的两方程湍流模型，该模型根据湍动能k和湍动能的比耗散率ω来计算涡黏系数，以封闭RANS方程。k－ω模型的湍流涡黏系数定义如下：

为了理解k－ω模型在三角翼旋涡流动中的作用，下面对k－ω模型的生成项进行分析。湍动能的生成项见式（4），与之相关的比耗散率方程生成项为：

由于该模型采用Boussinesq假设计算雷诺应力，湍动能的生成项变为：

从k和ω方程的生成项定义中，可以明显地看出，它只依赖于平均流动的应变率而没有考虑旋度的影响。然而涡核区域为高旋度区域，这种过度的简化导致涡核区域黏性过大，使得预测的旋涡耗散偏大，导致旋涡较弱，并且不能持续，迅速耗散。

为了使标准Wilcoxk－ω模型可以准确预测涡核区域的流动结构，Brandsma等［2］提出了两种不同的旋转修正方法。这些方法建议控制湍动能的生成项，进而控制涡核区域的湍流涡黏系数。第一种方法是直接把耗散项作为限制器来限制k方程的生成项，第二种方法是在流动的高旋度区域增加ω方程的生成项。本文采用第二种旋转修正方法，为了在合理的区域应用旋转修正，引入一个探测因子来区分剪切层和涡核。这个因子定义为平均应变率张量和平均旋转张量大小的比值：

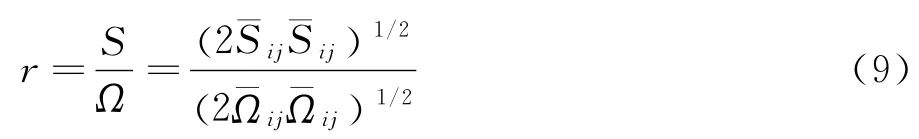
在剪切层内，应变率张量和旋转张量的大小几乎相等，r≈1，在涡核区域，流动接近旋转状态，r1。修正后的生成项定义为：

Pωnew等于ω方程的生成项除以min （r2，1），即：

采用这一修正后，加强了ω方程的生成项，使ω增加，也就更快的耗散k，减小了涡核区域的湍流涡黏性，涡核就不会被过快耗散，改进之后的模型称之为Pω增强型k－ω湍流模型。

2 计算模型

几何模型采用VFE－2实验中Chu和Luckring［4］在美国国家航空航天局（NASA）国家跨声速实验室（National Transonic Facility，NTF）风洞中使用的尖前缘三角翼模型。模型几何尺寸如图1所示，三角翼的根弦长Cr＝0.980m，翼展b＝0.914m，前缘后掠角φ＝65°，机翼面积S＝0.448m2，展弦比AR＝1.86。

3 数值模拟结果分析

首先研究计算网格对计算结果的影响，然后选用合适的计算网格，与标准Wilcoxk－ω湍流模型计算结果进行对比分析，验证Pω增强型k－ω湍流模型的适用性。本文对VFE－2实验中亚声速和跨声速条件下不同的流动状态进行了数值模拟。为方便叙述，各计算状态用表1中对应编号表示。

图1 65°后掠三角翼模型［12］Fig.1 Geometry of the 65°swept leading edge delta wing

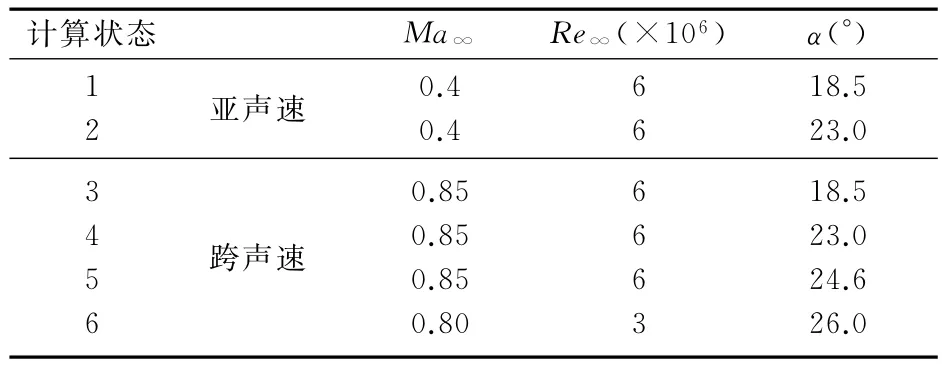
表1 计算状态对比Table 1 CFD cases chosen for summary comparison

3.1 网格影响分析

本文网格采用了H－O型网格拓扑。为了分析网格影响，相对粗网格，对三角翼前、后缘，支架顶点和物面法向区域网格进行加密处理。图2为密网格的拓扑结构、物面网格和空间网格切片，部分网格分布参数见表2。

图2 三角翼拓扑结构及计算网格示意图（fine grid）Fig.2 Mesh and grid topology around the delta wing

表2 计算网格量对比Table 2 Comparison of computational grid size

进行网格影响分析选用的计算状态为：Ma∞＝0.85，α＝23.0°，Re∞＝6×106。在文献［12］中，NASA NTF风洞试验数据显示三角翼上翼面并未发生主涡破裂现象，该迎角与发生涡破裂的临界迎角接近，而文献［12］的CFD方法预测出了涡破裂现象。

图3为选用Pω增强型k－ω湍流模型，粗、密网格的CFD计算结果对比，表明粗、密网格均预测出了三角翼上翼面的主涡峰值和二次涡峰值，前三个站位处，密网格预测的主涡和二次涡峰值均高于粗网格，更接近于试验数据。x／cr＝0.8站位处，粗网格预测的主涡峰值及站位与试验结果吻合良好，但沿展向外侧压力分布均低于试验数据，二次涡峰值不明显；密网格预测的主涡和二次涡峰值均高于试验数据。x／cr＝0.95站位处，粗网格预测的主涡峰值与试验数据吻合较好，但主涡形态较为平滑，密网格预测的主涡峰值偏高，但主涡形态与试验数据接近（即沿展向方向，在主涡外侧的压力系数曲线更为陡峭）。

上述对比表明，两套网格均较为准确地预测出了主涡和二次涡结构，网格密度达到研究要求。为了更为准确地预测绕三角翼旋涡流动中的分离涡、剪切层、激波与涡的干扰现象等，本文后续的研究均采用密网格。

图3 不同网格密度在不同展向站位物面压力系数曲线对比Fig.3 Comparison of surface pressure distribution between coarse and fine grid

3.2 亚声速旋涡流动

3.2.1 涡破裂前的状态——状态1

状态1的自由来流马赫数为Ma∞＝0.4，迎角α＝18.5°，为中度迎角，该状态下绕三角翼上翼面旋涡流场未发生涡破裂。图3给出了该状态的数值模拟结果，其中图4（a）左侧为采用标准k－ω湍流模型计算的物面压力系数分布，右侧为Pω增强型k－ω湍流模型的计算结果，并给出了沿三角翼5个流向站位（x／cr＝0.2，0.4，0.6，0.8，0.95）的物面压力系数分布与NASA NTF风洞试验数据的比较。通过对比可以看出，标准k－ω模型和Pω增强型k－ω模型均预测出了三角翼上翼面的主分离涡结构，但k－ω模型仅预测出了主涡的位置，不同站位处的主涡吸力峰峰值均低于试验数据，且主涡宽度较宽，没有预测出二次涡。Pω增强型k－ω湍流模型预测的主涡峰值和主涡宽度均与试验值吻合良好，且预测出了二次涡吸力峰，但吸力峰值低于试验数据，二次涡吸力峰的展向站位也比试验数据靠近机翼内侧，这是由于在计算中没有考虑横流转捩导致的。

图4（b）为不同站位切片上速度分量U等值线分布图，可以看到清晰的主涡结构，主涡没有发生涡破裂。二次涡结构靠近机翼表面，不够清晰，而图4（a）中x／cr＝0.95站位二次涡位置附近压力峰值消失，分布较为平坦，表明在三角翼后缘附近发生了涡破裂。

3.2.2 涡破裂后的状态——状态2

该亚声速状态发生了涡破裂现象，迎角为α＝23°，和状态1一样给出了标准k－ω模型和Pω增强型k－ω模型的计算结果，如图5（a）所示。通过对比同样可以明显地看出，标准k－ω模型预测的主涡吸力峰值偏低，宽度偏大，主涡强度较弱；Pω增强型k－ω模型预测的主涡吸力峰值与试验数据吻合良好，仅x／cr＝0.80站位处偏高，二次涡峰值高于试验数据。从图4（b）后两个站位切片的速度分量U等值线图及沿涡轴流线可以明显地看出，在三角翼后缘附近，主涡和二次涡均发生了涡破裂。

图5 状态2计算结果Fig.5 Computational results for case 2

3.3 跨声速旋涡流动

3.3.1 涡破裂前的状态——状态3

图6是跨声速状态下涡破裂前的计算状态，α＝18.5°。该状态下，标准k－ω模型没有模拟出明显的主涡结构，主涡吸力峰也不明显，x／cr＝0.20和0.4站位压力系数峰值远低于试验结果；而Pω增强型kω模型预测出了清晰的主涡和二次涡结构，x／cr＝0.20和0.4两个站位处主涡峰值稍低于试验数据，且沿展向方向稍靠近机翼内侧，x／cr＝0.60处预测峰值稍高，沿展向方向稍靠近机翼外侧，最后两个站位与试验数据吻合良好。此外，各个站位处的二次涡峰值均高于试验值。

图6 状态3计算结果与试验数据对比Fig.6 The comparison between the computational results and the experimental data for case 3

3.3.2 涡破裂后的状态——状态4、5

由文献［11－12，14］可知，跨声速下，随着迎角的增加，由于正激波的干扰作用，三角翼上主涡会发生突然的涡破裂现象。当Ma∞＝0.85时，VFE－2尖前缘三角翼发生涡破裂的临界迎角为24.6°，在该迎角下，支架前端正激波的干扰导致主涡在x／cr＝0.60附近发生了涡破裂。

图7为采用标准k－ω模型预测α＝23°时的物面压力分布，从x／cr＝0.60站位处主涡峰值减弱，最后两个站位处主涡峰值消失，变得较为平坦可以明显地看出，当α＝23°时已经发生了涡破裂，表明标准k－ω模型预测的临界迎角偏小。此外，与试验数据对比可知，标准k－ω模型并未预测出明显的二次涡结构，压力系数曲线与α＝24.6°的试验数据更为接近。

图7 标准k－ω模型计算的状态4结果Fig.7 The comparison between computational results of standard Wilcoxk－ωmodel and experimental data for case 4

图8为采用Pω增强型k－ω模型计算的状态4、5状态结果。图8左侧为α＝23°迎角下的计算结果，该状态未发生涡破裂现象，通过物面压力系数云图可以看出清晰的主涡和二次涡结构，与试验数据对比可知，各个站位计算结果与试验数据吻合良好；图8右侧为α＝24.6°迎角下的计算结果，由物面压力系数云图可以看出，该状态在x／cr＝0.60位置附近发生了涡破裂现象。各个站位压力系数曲线与试验值吻合良好，前两个站位处主涡和二次涡吸力峰均比较清晰，x／cr＝0.60站位处主涡峰值降低，这是由于激波干扰导致主涡强度减弱引起的，后两个站位处由于发生了涡破裂现象，主分离涡结构消失，压力分布变得较为平坦。Pω增强型k－ω模型准确地模拟出了这一复杂现象，表明Pω增强型k－ω模型适用于绕三角翼跨声速流场的数值模拟。

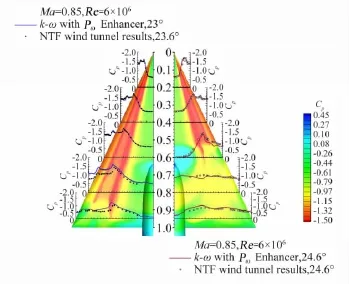
图8Pω增强型k－ω模型计算的状态4、5结果与试验数据对比Fig.8 The comparison between the computational results ofk－ωwithPωenhancer model and the experimental data for case 4and case5

3.3.3 轴向流动预测的验证——状态6

为了进一步考核Pω增强型k－ω模型对涡破裂前旋涡流场轴向流动的预测能力，与konrath等［21］在DLR的PIV试验结果进行了对比。选择对比的实验状态为Ma＝0.8，α＝25.9°，Re＝3×106。CFD计算选用迎角为α＝26°，其他状态参数与试验相同。

图9（a）～（f）为x／cr＝0.5、0.55、0.6、0.7、0.75和0.8站位处采用PIV测量出的速度分量u′（u′＝U／V∞）切片云图，试验中，该状态的涡破裂位置在x／cr＝0.6～0.7之间，图10（a）～（f）给出了采用Pω增强型k－ω模型计算出的与试验相同站位的无量纲速度分量u′切片云图。通过对比可以看出，在x／cr＝0.5站位，数值模拟结果与试验结果一样，主涡均呈扁平形状，试验的主涡形状更为扁平，涡核的展向和法向位置基本一致。在x／cr＝0.55处，主涡特性与前一站位基本一致，CFD和试验预测的二次涡均出现了涡破裂。x／cr＝0.6处，两者出现了较大差异，从图9（c）可以看出，主涡结构仍然存在，但与前两个站位相比，由于接近涡破裂位置，主涡强度已经明显减弱，变得不稳定。CFD方法预测的涡破裂位置在x／cr＝0.59处（从图10可以看出），因此，CFD方法预测结果中，x／cr＝0. 6已处于涡破裂之后。后三个站位均处于涡破裂之后，PIV和CFD的速度云图基本一致。

图9 PIV显示的速度分量u′切片云图［21］Fig.9 Velocity componentu′contours for PIV

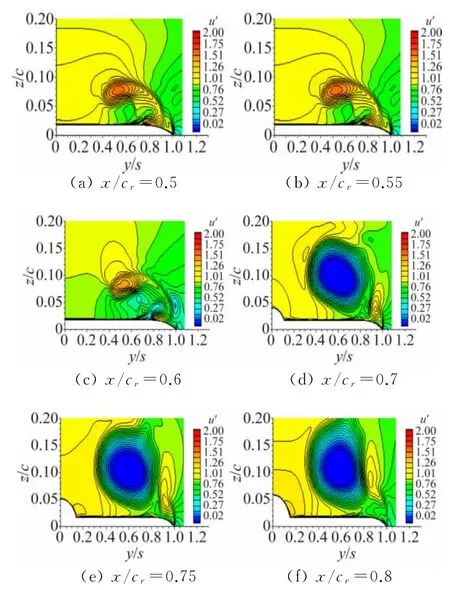
图10 状态6计算所得的速度分量u′切片云图Fig.10 Velocity componentu′contours for computational results of case 6

图11给出了本文CFD方法和Glassgow大学的CFD方法［21］（使用PMB（Parallel Multi－Block）流场求解器，基于多块结构化网格求解非定常RANS方程，控制方程的空间离散采用格心格式的有限体积法。其中，对流通量项的离散采用Osher和Roe迎风型数值通量，采用MUSCL变量插值方法获得二阶空间离散精度，Van Albada限制器消除激波附近的非物理振荡；粘性项离散采用二阶中心差分格式；定常计算采用隐式时间推进格式；湍流模型的处理与本文类似，采用对耗散率方程进行旋转修正的k－ω模型）计算的涡轴处无量纲速度分量u′分布与DLR试验数据的对比，试验给出了x／cr＝0.5、0.55和0.6站位处涡轴上三个点的速度u′，分别为：1.962（x／cr＝0.5处）、1.870（x／cr＝0.55处）、1.522（x／cr＝0.60处）。Glassgow大学和本文CFD方法预测的主涡轴线上u′最大值分别为1.864（x／cr＝0.378处）和1.879（x／cr＝0.55处），可以看出，本文的预测值更接近试验结果。CFD方法预测的涡核轴向速度最大值均低于试验数据，这可能是CFD方法预测的涡破裂位置靠前的原因。

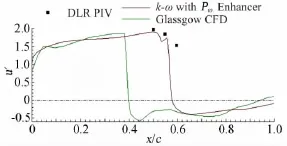
图11 涡核轴线上速度分量u′与试验PIV数据对比Fig.11 Comparison of velocity componentu′through vortex core between computational results and experimental PIV data for case 6

4 结 论

采用Pω增强型k－ω湍流模型，通过对尖前缘三角翼亚声速和跨声速绕流的数值模拟，可以得出以下结论：

1）Pω增强型k－ω湍流模型能够增加旋涡流动高旋度区域ω方程生成项，减小旋涡区域的湍流涡黏系数，而其他区域保持标准Wilcoxk－ω湍流模型基本特性，适用于绕三角翼的亚声速和跨声速旋涡流动数值模拟。

2）Pω增强型k－ω湍流模型能够准确预测出主涡吸力峰值和主涡的展向位置，但预测的二次涡峰值偏高，这与采用全湍流计算，未考虑转捩影响有关。

3）Pω增强型k－ω湍流模型能够准确地预测出跨声速下激波干扰导致主分离涡破裂的临界迎角及涡破裂位置。

［1］Nelson R C，Pelletier A.The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers［J］.Progress in Aerospace Sciences，2003，39（2－3）：185－248.

［2］Brandsma F J，Kok J C，Dol H S，et al.Leading edge vortex flow computations and comparison with DNW－HST wind tunnel data［C］／／Proceeds of the RTO／AVT Symposium on Vortex Flows and High Angle of Attack.NATO RTO／AVT，2001.

［3］Earnshaw P B.An experimental investigation of the structure of a leading edge vortex［R］.RAE Technical Note No.Aero.2740，Royal Aeronatical Establisment，March 1961.

［4］Chu J，Luckring J M.Experimental surface pressure data obtained on a 65°delta wing across Reynolds number and Mach number ranges：Volume 1－sharp leading edge［R］.NASA Technical Memorandum 4645，NASA Langley Research center，February 1996.

［5］Klute S M，Vlachos P P，Telionis D P.High speed digital particle image velocimtery study of vortex breakdown［J］.AIAA Journal，March 2005，43（3）：642－650.

［6］Jobe C E.Vortex breakdown location over 65°delta wing empiricism and experiment［R］.AIAA 1998－2526.

［7］Konrath R，Schrder A，Kompenhans J.Analysis of PIV results obtained for the VFE－2 65°delta wing configuration at sub－and transonic speeds［R］.AIAA Paper 2006－3003.

［8］Schrder A，Agocs J，Frahnert H，et al.Application of stereo PIV to the VFE－2 65°delta wing configuration at sub－and transonic speeds［R］.AIAA 2006－3486.

［9］Morton S A，Forsythe J，Mitchell A M，et al.DES and RANS simulations of delta wing vertical flows［R］.AIAA 2002－0587.

［10］Mitchell A M，Morton S A，Forsythe J R，et al.Analysis of delta wing vortical substructures using detached eddy simulation［J］.AIAA Journal，2006，44（5）：964－972.

［11］Schiavetta L A，Boelens O J，Fritz W.Analysis of Transonic Flow on a slender delta wing using CFD［R］.AIAA 2006－3171.

［12］Schiavetta L A，Boelens O J，Crippa S，et al.Shock effects on delta wing vortex breakdown［R］.AIAA 2008－395.

［13］Wang GuangXue，Deng Xiaogang，Liu Huayong，et al.Application of high－order scheme（WCNS）at high angles of incidence for delta wing［J］.Acta Aerodynamica Sinica，2012，30（1）：28－33.（in Chinese）王光学，邓小刚，刘化勇，等.高阶精度格式WCNS在三角翼大迎角模拟中的应用研究［J］.空气动力学学报，2012，30（1）：28－33.

［14］Li Xile，Yang Yong，Zhang Qiang，et al.Numerical simulation of shock／vortex interaction in transonic flow around a delta wing［J］.Acta Aeronautica et Astronautica Sinica，2013，34（4）：750－761.（in Chinese）李喜乐，杨永，张强，等.绕跨声速三角翼的激波／涡干扰流场数值模拟［J］.航空学报，2013，34（4）：750－761.

［15］Anderson J D.Fundamentals of aerodynamics［M］.2nd edition，McGraw－Hill International Editions，1991，356－364.

［16］Deléry J M.Aspects of vortex breakdown［J］.Progress in Aerospace Sciences，1994，30（1）：1－59.

［17］Hall M G.Vortex breakdown［J］.Annual Review of Fluid Mechanics，1972，4：195－218.

［18］Spall R E，Gatski T B，Grosch C E.A criterion for vortex breakdown［J］.Physics of Fluids，1987，30（11）：3434－3440.

［19］Robinson B A，Barnett R M，Agrawal S.Simple numerical criterion for vortex breakdown［J］.AIAA Journal，1994，32（1）：116－122.

［20］Wilcox D C.Reassessment of the scale determining equation for advanced turbulence models［J］.AIAA Journal，26（11）：1299－1310.

［21］Lucy Schiavetta.Evaluation of URANS and DES predictions of vortical flows over slender delta wings［D］.Department of Aerospace Engineering University of Glassgow，February 2007.

Application of k－ωwith Pωenhancer turbulence model to delta wing vortical flows

Zhang Dongyun1，Li Xile2，＊，Yang Yong3，Zhang Qiang3
（1.Shanghai aircraft design ＆Research Institute，Commercial Aircraft Corporation of China Ltd，Shanghai 201210，China；2.China Academy of Aerospace Aerodynamics，Beijing 100074，China；3.National Key Laboratory of Science and Technology on Aerodynamic Design and Research，Northwestern Polytechnical University，Xi’an 710072，China）

The production ofkωwithin standard Wilcoxk－ωturbulence model is dependent on the mean strain－rate of the flow and does not take the rotation rate into account，resulting in the prediction of a weak vortex which can’t be sustained and diffuses quickly.A suitable sensor is defined to distinguish between shear layers and vortex cores，to increase the production of the dissipation rate（ω）within regions of highly rotational flow.k－ωwithPωenhancer turbulence model is applied to RANS solver for structured grid.Subsonic and transonic flows around a 65oswept leading edge delta wing are simulated numerically.The computational results are compared with detailed experimental data obtained from a series of wind tunnel tests in the NTF at NASA and DNW－TWG at DLR.The comparisons show that thek－ωwithPωenhancer turbulence model produces better results when it comes to capturing the vortex core，the critical angle of attack and the position of vortex breakdown at subsonic and transonic flows，thus is suitable for simulating the vortical flow around delta wing.

k－ωturbulence model；production；delta wing；transonic；critical angle of attack；vortex breakdown

V211.3

Adoi：10.7638／kqdlxxb－2015.0200

0258－1825（2016）04－0461－08

2015－11－25；

2016－03－01

张冬云（1985－），男，安徽合肥人，工程师，主要从事民用飞机气动设计与CFD研究.E－mail：zhangdongyun＠comac.cc

李喜乐（1983－），男，河南洛阳人，博士，工程师，主要从事飞行器设计与CFD研究.E－mail：lxl1027＠163.com

张冬云，李喜乐，杨永，等.Pω增强型k－ω湍流模型在三角翼旋涡流动的应用［J］.空气动力学学报，2016，34（4）：461－467.

10.7638／kqdlxxb－2015.0200 Zhang D Y，Li X L，Yang Y，et al.Application ofk－ωwithPωenhancer turbulence model to delta wing vortical flows［J］.Acta Aerodynamica Sinica，2016，34（4）：461－467.