感知 感受 感悟——《平均数》教学片断与思考

季正伟

【教学片断】

一、在“比”中感知平均数的意义

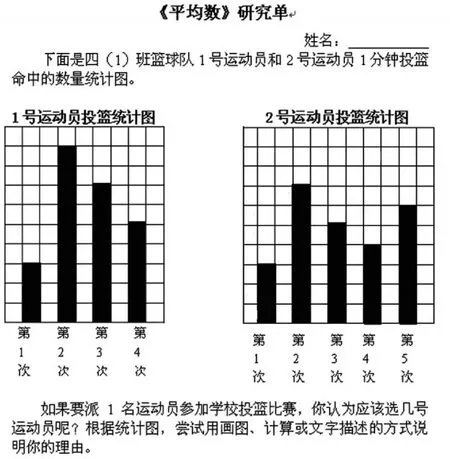
师：如果要派1名运动员参加篮球比赛，你认为应该选几号运动员？

生：1号选手共投中24个，2号选手共投中25个，所以选2号选手。

生：1号4次投中了24个，2号5次才投中了25个，所以比较总数不合适。

师：既然大家觉得两个人投篮的次数不同，比较总数不公平，那怎样比才合理呢？

生：我把1号运动员第2次移3个给第1次，把第3次移1个给第4次，这样1号运动员每次都投中了6个球；2号运动员我是把第2次移2个给第1次，把第5次移1个给第4次，这样2号运动员每次都投中5个球。6比5大，说明1号比2号水平高。

师：大家能看懂他的意思吗？（再找一名学生说一说）为什么要移？

生：这样1号运动员的水平就是6个，2号运动员的水平就是5个。

师：那移之后的这个6表示什么？

生：6表示1号运动员的水平。

生：6表示1号的平均数。

师：6能表示具体哪一次的个数吗？

生：6个不表示哪一次投中的个数，而是表示1号运动员这4次的整体的水平，也就是这4个数的平均数。就好比如这次我们单元练习班级平均分是92分，92分不代表哪一个同学的成绩，而是代表我们班整体的水平。

师：那移之后的5表示什么呢？

生：5表示2号运动员5次平均每次投中5个球，代表2号运动员的整体水平。

师：数学上把这样的方法叫做“移多补少”，通过“移多补少”我们能找出一个数表示一组数据的整体水平，这个数就叫做“平均数。”还有其他方法比较吗？

生：我是计算的，先算出1号运动员一共投中24个球，再除以一共投了4次，算出他平均每次投中6个；2号运动员也是一样，先算出一共投中25个球，再除以5次，算出平均每次投中5个，6比5大，所以应该派1号运动员去。

师：这样的方法数学上叫做“求和平分”，虽然两个同学介绍的方法不一样，但是存在什么联系呢？

生：都是变成一样多了。

生：移多补少是把多的拉下来给少的，使每次一样多。求和平分是先算出总数再平均分，也是使每次一样多。我觉得这是它们一样的地方。

师：不管是哪种方法，目的是让每个数都一样，这里的6就是 3、9、7、5 的平均数，而 5则是 3、7、5、4、6 的平均数，它们代表了两个人投蓝的整体水平。回忆一下，咱们解决谁的水平高这个问题的过程，其实就是我们认识平均数的过程，想想你对平均数有了什么认识？

生：平均数不代表哪一次的水平，而是代表运动员的整体水平。

生：可以用“移多补少”和“求和平分”这两种方法求平均数。

【教学思考：这节课，我用“选几号运动员参加比赛”作为引领学生独立思考、小组讨论、展示分享的主线，让学生通过解决这样一个与生活结合密切的问题来感知平均数的产生、意义以及作用。谁的水平高中的“水平”其实就是平均数的代名词，这一个简洁而易懂的问题，既贴近学生的生活，又调动了学生已有的知识储备和生活经验 。“移多补少”、“求和平分”等形象化的呈现方式是促进理解的最佳途径，在移多补少的基础上，让学生展示求和平分的方法，从而体会求平均数一般有两种方法。】

二、在“选”中感受平均数的方法

【教学片断】

师：平均每个笔筒里有多少支铅笔？

生：6支。

师：反应这么快，怎么知道的？

生：移多补少。

师：这一次平均每个笔筒里有多少支铅笔？

师：为什么反应没刚才快了？这时用什么方法求平均数更合适？

生：求和平分。

师：通过这两个练习，你对平均数又有了哪些新的认识？

生：数据少且接近时用“移多补少”更快一些，数据多且数据相差较大时用“求和平分”更合适一些。

【教学思考：通过两个练习的对比，使学生感受到面对不同的平均数问题应灵活选择不同的方法解决，当面对数量较多且悬殊较大的数据时，选用求和平分的计算方法更合理。】

三、在“变”中感悟平均数的特征

【教学片断】

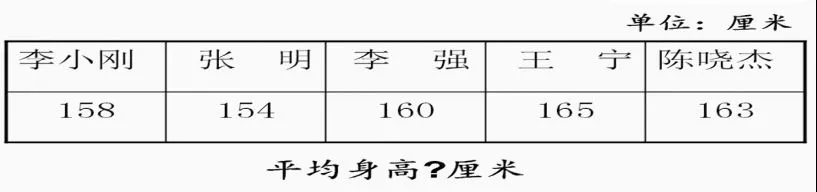
师：大家觉得这次应该选择什么方法求平均身高？

生：求和平分。

师：估一估，你觉得平均数可能是多少？

生：160厘米。

生：161厘米。

生：159厘米。

师：会不会是170厘米呢？

生：不可能，平均数要移多补少，最高的是165厘米，他还要移些给矮的同学，平均身高只会比165矮。

师：那肯定比谁高呢？

生：比154厘米高，因为高的同学还要移些给他，肯定要比154厘米多。

师：看来平均数是有一个范围的。

生：平均数比最小的数大，比最大的数小。

生：我还知道平均数一般接近最大数和最小数中间的一个数。

师：具体是多少呢？算一算。（计算出平均身高是160厘米）

师：通过刚才的练习，你对平均数又有了哪些新的认识？

生：平均数是有范围的，它比最小的数大，比最大的数小。

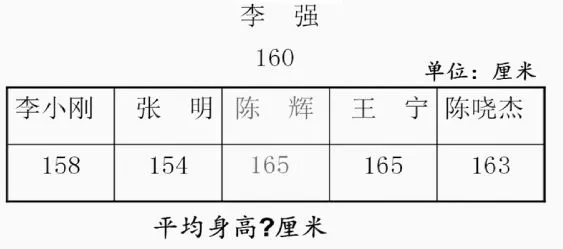
师：一天，由于李强请假了，教练将身高160厘米的李强换成了165厘米的陈辉，现在篮球队的平均身高和原来比有什么变化？

生：我是这样认为的，原来平均身高是160厘米，李强身高也是160厘米，他不要移别人的，也不要移给别人，现在陈辉身高是165厘米，他还可以给别人一些，所以平均身高会增加。

生：原来李强160厘米换成陈辉165厘米，他们的身高总和就多了5厘米，但是人数没变，我们可以把这多的5厘米分给5个人，每人会多出1厘米，所以我可以知道现在篮球队五人的平均身高是161厘米。

师：如果换成170厘米的运动员呢，平均身高会多多少？那换成155厘米的运动员呢？

师：通过刚才的练习，你对平均数又有什么新的认识？

生：一组数据中只要有一个数据变化了，平均数就会发生变化。

师：难怪有人这样形容平均数：“平均数很敏感，任何一个数的风吹草动，都会使平均数发生变化。”现在看来这话有道理吗？所以平均数是具有“不稳定”性的。

【教学思考：在计算平均身高前让学生进行估算，学生根据经验能感觉出大概的平均身高，在学生的不断补充中悟出了平均数的范围，平均数都比最小的数大，比最大的数小。】