基于改进的Bernoulli矩阵压缩感知图像重构算法

蔡荣文杭州万向职业技术学院，浙江杭州310023



基于改进的Bernoulli矩阵压缩感知图像重构算法

蔡荣文
杭州万向职业技术学院，浙江杭州310023

摘要：为克服传统测量矩阵稳定性差的弱点，本文利用Logistic混沌序列优良的随机性质，对Bernoulli测量矩阵进行改进，提出一种复杂度很低的混沌Bernoulli测量矩阵。通过Logistic混沌系统产生混沌序列，之后运用符号函数进行映射生成Bernoulli分布的随机矩阵，将该序列用来构造测量矩阵。实验结果表明，基于Bernoulli测量矩阵图像重构的信噪比优于Bernoulli矩阵和Gaussion矩阵，从而证明该算法的可靠性和有效性。

关键词：Bernoulli矩阵；混沌序列；Logistic系统；图像重构算法

压缩感知理论是近些年来重点研究的采样理论，最先由Donoho[1]和Cande[2]等人提出。压缩感知理论打破传统采样理论对采样频率的限制，在获取数据的同时实现采样信号的压缩，可以降低数据采样量、节约计算时间以及节约数据的存储空间。压缩感知理论主要涉及三个核心问题：（1）信号的稀疏变换；（2）设计测量矩阵；（3）构造重构算法。其中，测量矩阵设计质量的好坏直接影响后面重构信号的误差大小。当前测量矩阵主要分为确定性测量矩阵和随机性测量矩阵。

Lei Yu[3]运用混沌序列构造一个测量矩阵，实验结果表明构造出的矩阵满足RIP性质并且验证出该矩阵是可行的。顾国生等人[4]提出一种基于符号混沌系统的伪随机序列将其作为构造压缩感知观测矩阵，实验结果证明该方法是可行的和有效的，但该方法具有复杂度高和计算量大的缺点。

针对Bernoulli测量矩阵存在稳定性差的缺点，本文利用Logistic混沌序列优良的随机性质，对Bernoulli测量矩阵进行改进，提出一种复杂度很低的混沌Bernoulli测量矩阵。通过Logistic混沌系统产生混沌序列，之后运用符号函数进行映射生成Bernoulli分布的随机矩阵，将该序列用来构造测量矩阵。通过二维图像的不同随机矩阵的仿真对比发现，本文算法构造出的矩阵是有效的和可行的。

1　压缩感知

1.1改进的粒子群算法

假设一维信号X∈RN×1，X可通过一组N×N正交基ψ＝{ψ1，ψ2，…，ψN}进行表达，其表达式如公式（1）所示[5，6]：

公式（1）中，θk＝＜X，ψk＞，X，θ均为N×1维向量。当信号X在某个正交基ψ上当且有K＜＜N个非0系数θk，此时Ψ是信号X的稀疏基。

稀疏采样时，信号X可以被投影在测量矩阵Φ上，因此采样数据Y可以表示成：

其中，Y表示M×1的被测量矩阵，Φ表示M×N（M＜＜N）的测量矩阵。由公式（1）和公式（2）可以得到采样数据和变换矩阵之间的关系式（3）：

稀疏采样可以大大减少采集数据的数量，提高数据采集效率。然而，稀疏采样也会导致信号的重构和恢复出现“病态”问题。压缩感知理论认为信号重构问题可以转化成求解l0范数最小化问题[7]：

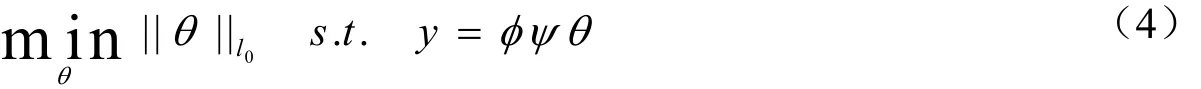
2　基于混沌矩阵的Bernoulli测量矩阵的构造

已知Logistic混沌系统的表达式如公式（5）所示：

公式（5）中，xn∈[-1，1]，µ∈[1.872，2.0]，当公式（5）的初始值x0＝0.23，0.37或0.7的时候，其产生的序列为混沌序列。

将Logistic混沌系统产生的混沌序列{xn}，通过公式（6）符号映射函数转换成新的映射序列{an}。

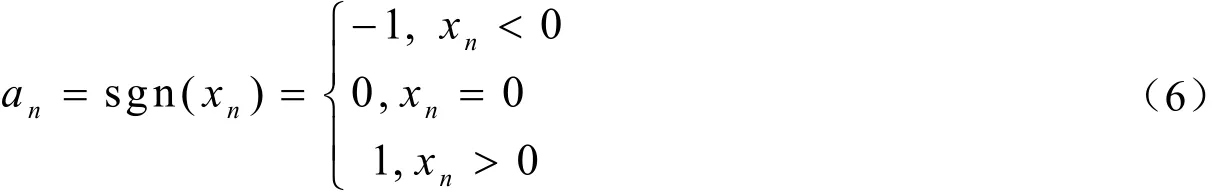
根据参考文献[9]可知，当µ＝2.0时，Logistic混沌系统产生的混沌序列xn符合Bernoulli分布，同时满足RIP性质，所以将Logistic混沌序列进行符号映射所产生的映射序列an作为压缩感知的测量矩阵。

混沌矩阵的Bernoulli测量矩阵的构造步骤如下：

（1）根据公式（5）Logistic混沌系统生成混沌序列{xn}，该序列长度为n，其中n＝M×N-1。依据反复实验对比的结果可知，当µ＝2.0时，初始值x0＝0.23，0.37或0.7时，它们重构误差分别为0.098，0.083，0.090，由此可知，本文选取初始值xo＝0.37，µ＝2.0。

（2）将步骤（1）生成的Logistic混沌序列通过公式（6）进行符号函数映射，生成映射序列{an}。

（3）设定截断长度为N，将映射序列{an}截断，构造出维度大小为M×N的测量矩阵Φ。

参考文献[5]中算法的复杂度远远大于o（N2），而本文提出算法的复杂度为o（M×N）（M＜＜N），复杂度远低于相关参考文献中算法的复杂度。

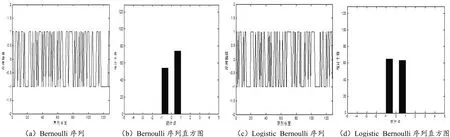
图1　序列和直方图对比图Fig.1　Comparison between sequence and histogram（a）Bernoulli sequence（b）Histogram of Bernoulli sequence（c）Logistic_Bernoulli sequence（d）Histogram of Logistic_Bernoulli sequence

由Logistic-Bernoulli和Bernoulli随机序列对比图和直方图对比图可知，Logistic-Bernoulli随机序列中1和-1的数量差不多多，比值接近于1，说明Logistic-Bernoulli随机序列的稳定性和平均性较好，优于未改进的Bernoulli随机序列。

3　基于Logistic-Bernoulli测量矩阵的OMP算法信号重构

3.1OMP算法

匹配追踪类方法进行信号稀疏重建的实质是求解最小lo范数的问题，本文采用正交匹配追踪（OMP）算法。OMP算法利用Gram-Schmidt正交化方法将所选原子进行正交处理，经过正交化之后的信号投影在正交原子的空间上，获得信号在原子投影空间上的信号分量和信号余量，之后运用同样方法继续分解信号余量。

匹配追踪类算法相关系数u，主要通过计算信号余量r和感知矩阵Φ中各个原子之间内积的绝对值获得[8]：

同时运用最小二乘法实现信号逼近和余量更新：

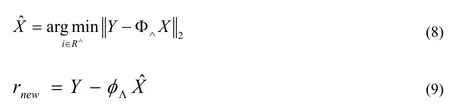
基于Logistic-Bernoulli测量矩阵的OMP算法的算法流程如下：

输入：维度大小为M×N的Logistic-Bernoulli测量矩阵Φ

Step1：初始余量ro＝Y，迭代次数n＝1，索引值集合Λ＝ø，J＝ø

Step2：计算相关系数u，并将u中最大值对应的索引值存入J中；

Step3：更新ΦΛ，其中Λ＝Λ∪J0；

Step5：若ǁrnew-rǁ≥ε2，令r＝rnew，n＝n＋1，转步骤Step2；否则，停止迭代。

3.2评价指标

假设W，H分别表示图像的宽度和高度，I，Î分别表示原始图像和重构图像。本文运用图像信噪比作为重构效果的评价指标。二维图像的信噪比公式如（10）所示：

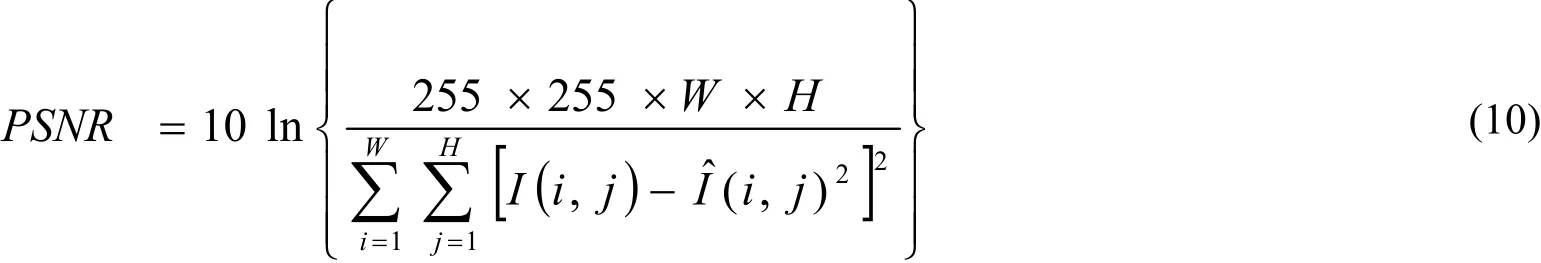
4　仿真实验

为了验证本文算法的有效性，同时为降低实验计算量，图像采用大小为256’256的标准测试图像，以Lena图像为研究对象，研究在压缩比等于0.5时，基于Logistic-Bernoulli测量矩阵、Bernoulli测量矩阵和Gaussion测量矩阵三者之间的图像重构效果，对比图如图2所示：

图2　不同测量矩阵的重构效果Fig.2　Reconstruction results of different measurement matrix（a）Lena image（b）Measurement matrix of Logistic_Bernoulli（c）Measurement matrix of Bernoulli（d）Measurement matrix of Gaussion

由图2不同测量矩阵的重构效果可知，基于Logistic-Bernoulli测量矩阵的图像重构效果优于Bernoulli测量矩阵和Gaussion测量矩阵的重构效果。为了进一步验证算法的有效性和可靠性，分别以Lena、Cameraman和Barbara三幅标准测试图像，对比不同压缩比下，重构图像的信噪比，其对比结果如图3所示：

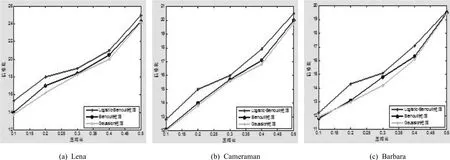
图3　不同图像，压缩比和信噪比的变化图Fig.3　Different image, variation of compression ratio and PSNR（a）Lena（b）Cameraman（c）Barbara

由图3不同图像，压缩比和信噪比的变化图可知，随着压缩比的提高，图像重构信噪比不断增加，此外基于Logistic-Bernoulli测量矩阵图像重构的信噪比优于Bernoulli矩阵和Gaussion矩阵，从而证明了本文算法的可靠性和有效性。

5　结论

针对传统测量矩阵具有随机性和平均性差的缺点，将Logistic混沌序列引入压缩感知理论，构造出新的Logistic-Bernoulli测量矩阵并将其应用于压缩感知代替传统的测量矩阵，构建出基于Logistic-Bernoulli测量矩阵的OMP信号重构算法。实验结果表明，基于Logistic-Bernoulli测量矩阵图像重构的信噪比优于Bernoulli矩阵和Gaussion矩阵，从而证明了本文算法的可靠性和有效性。

[1] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory，2006，52（4）:1289-1306

[2] Candes E.Compressive sampling[C]. Madrid，Spain:Proceedings of the International Congress of Mathematicians，2006

[3] Yu L，Barbot JP，ZhengG，etal.Compressivesensingwithchaoticsequence[J].IEEESignalProcessingLetters，2010，17（8）:731-734

[4]顾国生，战荫伟.一种混沌序列在压缩感知观测矩阵构造中的应用[C]//第十五届全国图像图形学学术会议，2010:111-114

[5] Candes E，Romberg J. Sparsity and incoherence incompressive sampling[J]. Inverse Problems，2007，23（3）:969-985

[6]方红，章权兵，韦穗.基于亚高斯随机投影的图像重建方法[J].计算机研究与发展，2008，45（8）:1402-1407

[7]方红，章权兵，韦穗.基于非常稀疏随机投影的图像重建方法[J].计算机工程与应用，2007，43（22）:25-27

[8]孙玉宝，肖亮，韦志辉，等.基于Gabor感知多成份字典的图像稀疏表示算法研究[J].自动化学报，2008，34（11）:1379-1387

Image Compressed Sensing Reconstruction Algorithm Based on Improved Bernoulli Chaotic Matrix

CAI Rong-wen
Hangzhou Wanxiang Ploytechnic,Hangzhou 310023，China

Abstract:To break through the shortcoming of poor stability in the traditional measurement matrix，this paper used an excellent stochastic property of Logistic to turn the Bernoulli measurement matrix into chaotic one with a very low complexity. Chaotic sequence was generated by Logistic chaotic system and then used the sign function to become the stochastic matrix of Bernoulli distribution to be used to construct the measurement matrix. Experimental results showed that signal-to-noise ratio of image reconstruction based on the chaotic Bernoulli measurement matrix was better than Bernoulli and Gaussion matrix，which proved the reliability and effectiveness of the proposed algorithm.

Keywords:Bernoulli measurement matrix；chaotic sequence；Logistic system；map reconstruction algorithm

作者简介：蔡荣文（1974-），男，浙江苍南人，本科，讲师，主要研究方向计算机应用. E-mail:wxxycrw@126.com

基金项目：浙江省高等学校访问学者教师专业发展项目:基于图像处理的火灾烟雾智能探测研究（FX2014196）

收稿日期：2014-10-11修回日期: 2014-12-23

中图法分类号：TP391.1文献标示码：A

文章编号：1000-2324（2016）01-0107-04