抗滑桩加固后边坡稳定性评价与桩位优化研究进展

宋英杰，陈文强，李长冬

(中国地质大学(武汉)工程学院，湖北武汉430074)

抗滑桩加固后边坡稳定性评价与桩位优化研究进展

宋英杰，陈文强，李长冬

(中国地质大学(武汉)工程学院，湖北武汉430074)

边坡失稳是影响人类工程建设活动安全性的一类常见的地质问题，抗滑桩是边坡治理工程中常用的防治措施之一，但是目前考虑加桩后边坡的稳定性研究较少。针对抗滑桩加固后的边坡稳定性评价和抗滑桩桩位布设优化问题的研究进展进行了概述，重点综述了:抗滑柱加固边坡的稳定性分析方法，即国内外在理论计算、数值模拟和物理模型实验三方面的研究成果，并对比分析了各自的优缺点;目前常用的抗滑桩最优布设分析方法，并指出了各自的适用条件;当前边坡工程中抗滑桩桩位优化研究的现状，并对今后的发展方向进行了展望，可为今后类似研究提供一定借鉴与参考。

边坡;抗滑桩;稳定性分析;桩位优化

近几十年来，伴随着国内外工程建设活动的蓬勃发展，作为自然界中广泛分布的一类地质体，边坡的稳定性分析及加固问题一直是工程领域的研究热点问题。工程实践表明，通过采取边坡加固措施如挡土墙、锚索、抗滑桩等可以显著提高边坡的稳定性，避免工程建筑遭受破坏。通过抗滑桩加固边坡是应用广泛的一种加固措施，目前关于抗滑桩加固边坡的稳定性分析已经发展了多种方法。抗滑桩的桩位布设问题不仅会影响边坡的稳定性，还与实际工程造价有关，合理地布设抗滑桩桩位能大大节约成本，因此很有必要对抗滑桩的合理桩位问题进行研究，但目前关于此问题的研究常由于采用不同的方法得出的结果往往有差异。鉴于此，本文针对抗滑桩加固后的边坡稳定性分析方法和抗滑桩桩位布设优化问题的研究进展进行了总结和分析，并指出当前边坡工程中抗滑桩合理桩位研究领域存在的主要问题，为工程实践和理论研究提供一定的借鉴与参考。

1 抗滑桩加固后的边坡稳定性分析方法研究进展

自20世纪50年代抗滑桩开始被应用于边坡的加固以来，大量的工程实践和理论研究都表明，通过抗滑桩来加固可能或已经滑动的边坡是一种行之有效的方法［1］。国内外许多学者都对抗滑桩加固边坡的稳定性分析进行了广泛的研究，目前主要的研究方法有理论计算、数值模拟、物理模型实验等几个方面。

1．1 理论计算

目前国内外用于计算抗滑桩加固边坡提供的抗滑力与加固后边坡的稳定性系数(也称稳定安全系数)的方法主要包括极限平衡法、极限分析法和强度折减法等。

1．1．1 极限平衡法

极限平衡法是以Mohr-Coulomb强度理论为基础，运用力学平衡原理对即将产生滑动破坏的潜在滑动面上的岩土体用静力平衡条件来求得边坡的稳定性系数［2］。当前国内外以极限平衡法为基础的方法主要有Fellenius法［3］、简化 Bishop法［4］、Morgenstern-Price法［5］、Spencer(1967，1973)法［6-7］、Sarma(1973)法［8］、Janbu(1973)法［9］和国内常用的推力传递法［10］等。

目前，抗滑桩加固边坡的稳定性计算大多是通过计算作用在抗滑桩上的主动土压力或剩余推力来得到边坡的稳定性系数。关于抗滑桩提供的抗滑力的计算方法，国内的计算方法主要可归纳为悬臂桩法和地基系数法［11］;国外Ito等通过运用极限平衡的方法和作者本人导出的作用在单排桩的横向力对地基塑性变形的理论方程(Ito-Matsui方程［12］)，进行了单排桩加固的边坡稳定性分析［13］;穆启超等［14］运用剩余推力法对抗滑桩加固新房村滑坡的可行性进行了研究。

极限平衡法的优点是原理简单、计算过程简便且得出的边坡稳定性分析结果可以应用于实际工程中，因此该法仍是边坡工程中广泛被应用的方法;但该法的缺点是:①需要事先假定滑动面，再通过安全系数的表达式反过来求解可能的滑动面，求解的过程需要通过迭代求解隐式方程组，求解结果存在误差;②对于非均质、分层岩土体，事先假设的滑动面与实际情况相差较大;③没有考虑岩土体的实际应力-应变状态，假设的岩土体的受力情况与实际不符。

1．1．2 极限分析法

极限分析法将岩土体视为理想刚塑性体，满足屈服准则、流动准则和小应变假设，根据所求得的极限解的大小可分为极限分析上限定理和下限定理［15］。由20世纪70年代金属塑性理论发展而来的极限分析法的实质就是通过找出某一个问题最大胆(上限解)和最保守(下限解)的解答后，再从中确定一个解作为问题的正确解。如果上限解等于下限解，则所得的解就是准确解［16］。

极限分析上限法也称能量法，这种方法认为岩土体为理想刚塑性体，然后利用连续介质的虚功原理和塑性力学的上限定理求解边坡稳定性问题。早期Chen［17］和很多学者都用能量法讨论了边坡的稳定性，其基本思路是:从变形协调出发，对于已设定的滑裂面建立协调的速度场，然后以内能耗散和外力功相平衡的原理为基础，得到相应的边坡稳定性系数。该方法假设滑动面如图1所示，为了简化，将坡体视为均质、各向同性和干燥的土体，滑动面的方程为［18］

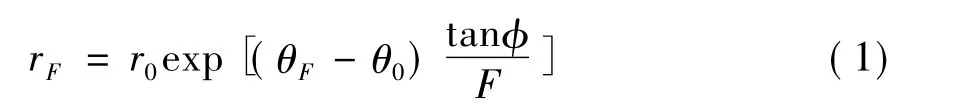
式中:r0为对数螺旋线关于O点的半径(m);rF为与角度θF(rad)有关的半径(m);为土体的内摩擦角(°);F为边坡稳定性系数。

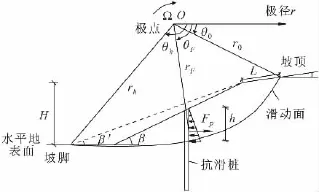
图1 单排桩加固的螺线形边坡滑动面破坏机制示意图［18］Fig．1 Rigid rotation collapse mechanism of slope reinforced with a row of piles

滑体关于O点的旋转角速度为Ω(rad/s)，根据能量法的基本原理，当外部荷载(包括重力)做功功率和内力能量消散功率相等时，坡体处于极限平衡状态。重力做功功率W1(kW)可以表示为［18］

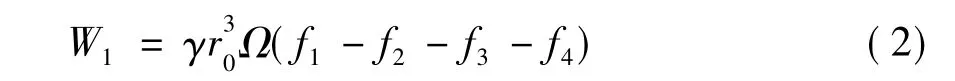
式中:γ为土体的重度(kN/m3);f1～f4为关于α(°)、θ0(rad)、θh(rad)(°)、β(°)和β'(°)的无量纲函数。

对于单排桩加固的边坡，内力所做能量消散功率包括滑动面土体内聚力的能量消散功率D1(kW)和桩体附近本身功率D2(kW)。内力做功功率可以表示为［18］

式中:c为土体的内聚力(kPa)。

桩体做功功率可以表示为［18］

式中:Fp为桩对单位宽度的滑体施加的力(kN/m)。

f1～f5的计算公式如下［18］:

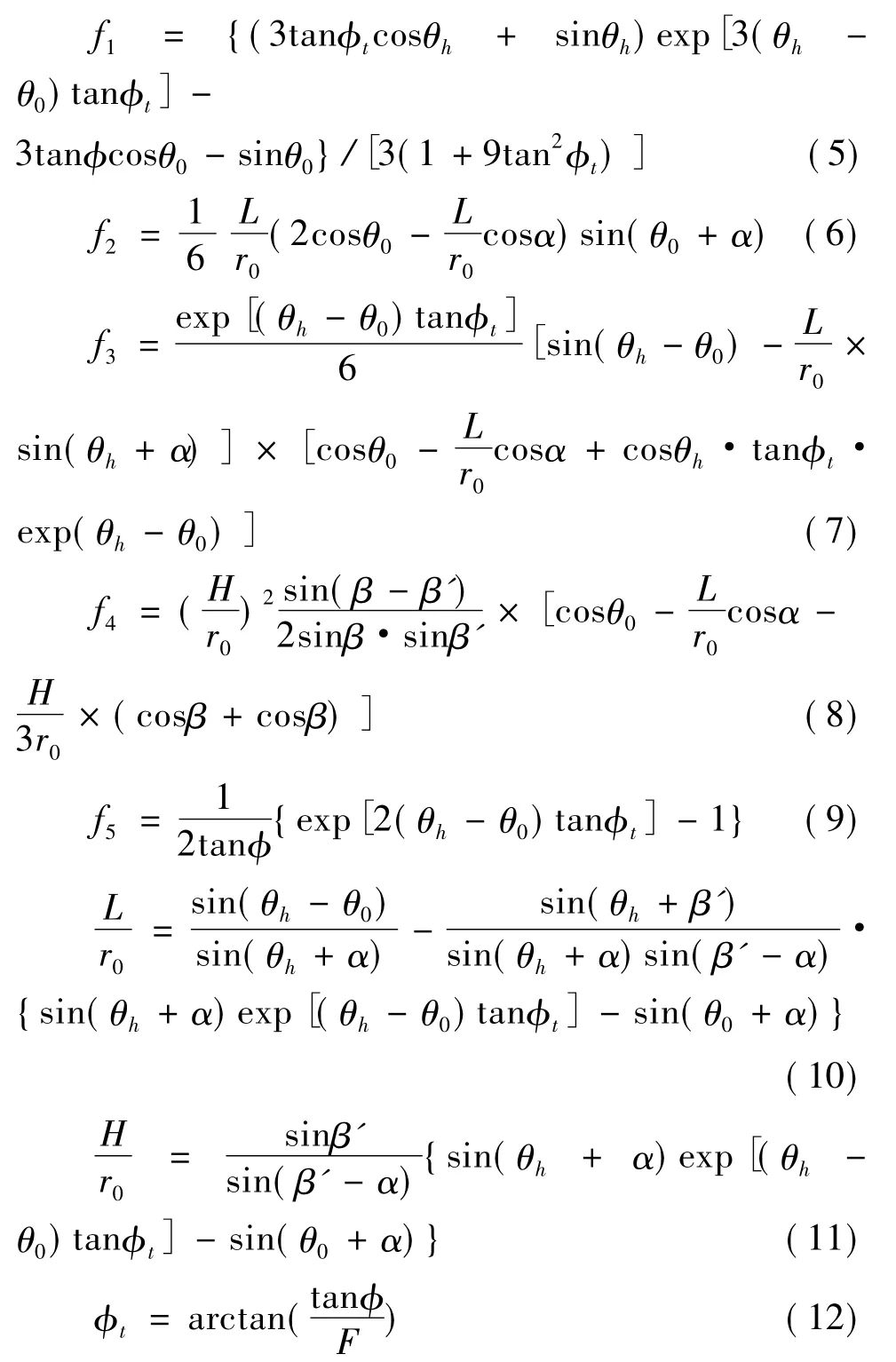
式中:L为坡面与坡顶的交点与滑动面与坡顶的交点之间的距离(m)，见图1;H为坡面与坡顶的交点至水平地表面间的距离(m);为土体的折减内摩擦角(°)。

D1和D2之和就是总的内能耗散，由外力功和内能耗散相平衡的原理可以推导出［18］:

Fp的计算公式为［18］

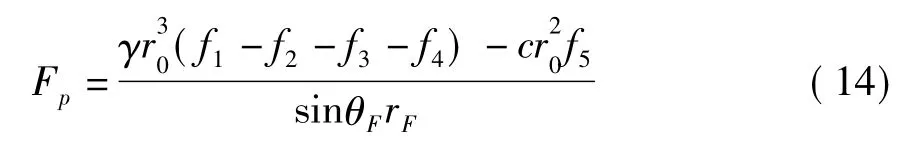
式中Fp可采用Ito和Matsuil的弹塑性理论来求得［13］。因为滑动面和地面之间桩的长度h与Fp的值是相关的，所以当每次选择一个新的滑动面时，要根据新选择的滑动面来计算Fp的大小，即运用公式来求得Fp从而确定一个新的稳定系数，这种方法比传统极限平衡法更方便且符合实际。

1．1．3 强度折减法

20世纪70年代末，Zienkiewice等［19］就已经提出将强度折减技术和有限元法结合起来。近年来，随着数值计算水平的发展，有限元强度折减法已成为比较常用的边坡稳定性分析方法。

Ugai［20］假定土体为理想的弹塑性材料，采用强度折减有限元法对直立边坡、倾斜边坡、非均质边坡及存在孔隙水压力的复杂边坡的稳定性进行了较为系统的研究，指出弹塑性折减有限元法具有较强的适应性。国内最早将强度折减法应用于边坡稳定性分析的是宋二祥，他采用强度折减法对边坡的稳定性进行分析，并以边坡中某一部位的位移作为收敛指标［21］。此外，针对当前强度折减弹塑性有限元法中存在的只对强度参数折减的问题，郑宏等［22］提出了应同时考虑力学参数的影响，并给出了相应的调整措施。

有限元强度折减法的优点是不用预先假定滑动面的形态、位置等，考虑了桩与土的应力-应变关系，与实际情况相符，并且可以求解出应力、位移等情况;缺点是评价塑性破坏的指标未统一，基于迭代数值计算的终止条件不明确，且对于非连续介质该方法不太实用，并存在一定误差。

1．2 数值模拟法

数值模拟法就是把科学研究和实际工程中的问题转变为数学模型，再运用数学方法来模拟实际问题，从而更为方便、迅速地探究其本质和规律，目前数值模拟法已被广泛应用于抗滑桩边坡加固工程研究中。常用的数值模拟软件主要有ABAQUS、FLAC3D、ANSYS等。如邵安东等［23］釆用有限元差分软件FLAC3D，以边坡稳定性系数作为主要的参数指标，对抗滑桩加固边坡的桩位优化进行了数值模拟分析，结果表明当抗滑桩设置在滑坡中部时，桩的支护效果可以达到最佳;戎斌斌［24］运用ABAQUS有限元软件对路堑和挖方公路边坡中常见的滑坡进行了模型简化，并选取弧形边坡的断面进行了抗滑桩桩位的三维有限元分析，结果表明呈矩形分布的抗滑桩的最优桩位处在弧形边坡的中下部区域;Reddish等［25］对桩在不同布设位置的通用边坡进行了量纲数值分析，结果表明一种能够提供递增的稳定性系数的稳定力的简单模型需要结合另一种模型，可以通过此模型来限制排桩的相互作用，从而得到桩距比例对稳定系数影响的直观估计。

1．3 物理模型试验法

物理模型试验可以精确地控制边坡的边界条件、抗滑桩和岩土体的材料特性，因此在研究桩-土相互作用时具有针对性和目的性，同时物理模型试验也具有时效性，可以研究其稳定性随时间的变化规律，还可用其结果验证理论计算和数值模拟结果的正确性。如余小马［26］结合工程实例对抗滑桩滑坡推力和桩前滑体的抗力分布问题以及抗滑桩合理位置确定问题进行了对比研究，实例研究表明:在抗滑桩设计中采用不同的滑坡推力和土体抗力分布形式时，对抗滑桩的内力计算和结构设计将产生较大的差异并影响其效果［26］;张涛等［27］通过开展悬臂式单根锚杆抗滑桩加固黄土滑坡的室内模型试验研究，结果表明:在滑坡推力作用下，悬臂式锚杆抗滑桩受荷段桩后受压、桩前受拉，而嵌固段桩后受拉、桩前受压，锚杆抗滑桩受力形式呈“S”曲线状;悬臂式锚杆抗滑桩的破坏模式主要为塑性铰弯折破坏，而土体中锚杆的破坏模式主要为弯剪-滑移破坏。

综上所述，目前国内外关于抗滑桩加固边坡后的稳定性评价的研究方法主要有理论计算、数值模拟和物理模型试验三个方面。在理论计算中，极限平衡法需要事先假定可能滑动的滑动面，采用条分的方法来逐条计算各条块的受力，该方法原理简单，但并没有考虑岩土体与桩的真实应力-应变状态，且引入的简化假定也与实际情况不符;极限分析法假定岩土体为理想的刚塑性体，应满足屈服准则、流动准则和小应变假设，可找出最可能的滑动面，但该法通常需要假定滑动面的形态;有限元强度折减法不用假定滑动面的位置、形态等，考虑了岩土体的真实应力-应变状态，并且可以求解应力、位移等情况，但该法评价塑性破坏的指标不统一，对于非连续介质也不太实用。相比于理论计算，数值模拟法和物理模型试验法可以获得更多的有关受力、位移等的真实情况，但数值模拟法不能很好地考虑桩与土之间的相互作用且该法往往依赖于数值计算技术，过程较复杂;物理模型试验法不仅很好地考虑了桩与土的相互作用，且具有时效性，能对理论计算和数值模拟的结果进行验证。

2 抗滑桩桩位布设优化研究进展

目前关于抗滑桩的优化设计方面已经取得一些成果，但关于抗滑桩的桩位布设优化方面成果并不多且得出的结论也有所差异。抗滑桩的桩位布设不仅会影响边坡的稳定性，还会影响抗滑桩的设计桩长，从而对工程造价产生影响，因此有必要对抗滑桩的桩位布设进行优化设计，找出合理布设的位置。本文认为抗滑桩的最优布设位置是指将边坡的稳定性系数提高到设计安全系数时抗滑桩所需提供的抗滑力取得最小值的位置;最安全布设位置是指使边坡取得最大稳定性系数的位置。目前常用的抗滑桩最优布设分析方法主要有极限平衡法、极限分析法、有限元强度折减法、数值模拟法、物理模型试验法等。

2．1 极限平衡法

极限平衡法在抗滑桩桩位优化中被广泛应用，其通过研究抗滑桩加固边坡时所提供的抗滑力和稳定安全系数等可以对抗滑桩的桩位进行优化，得出抗滑桩最优布设位置和最安全布设位置等。如Ito等［12］研究表明:当抗滑桩的桩位位于边坡中上部时对边坡稳定性的影响最大;Poulos［28］研究指出，应将抗滑桩桩位布设于临界破坏楔体中部附近，以此来避免仅仅将破坏面定在桩的前面或后面;Lee等［29］通过运用简化的Bishop滑动圆弧法计算得出:对于均质土坡，最有效的布设桩位是坡顶和坡脚处，对于下伏硬岩、上部为软岩的双层土坡，最有效的布设桩位应位于边坡中部与坡顶之间;Hassiotis等［30］通过运用莫尔圆方法和公式计算得出，抗滑桩布设的最安全位置为边坡的坡顶附近，特别是边坡很陡的情况;王亮清等［31］基于剩余推力法，以湖北省巴东县宋家屋场滑坡为例，提出用“结构设计法”来确定抗滑桩的桩位，研究表明:抗滑桩布设在滑坡体中部时的弯矩和剪力比较小，即工程量和工程所需成本较小，此位置即为抗滑桩的合理布设位置;李家平等［32］介绍了一种基于瑞典法和简化Bishop法来分析抗滑桩加固边坡的极限平衡法，通过与某闸室岸坡工程算例结合，得到如下结论:①抗滑桩的布设能够有效地提高边坡的稳定性;②当抗滑桩的布设通过边坡潜在危险滑动面最低点时，其加固边坡的效果最好;③抗滑桩的布设会改变边坡潜在危险滑动面的位置。

运用极限平衡法研究抗滑桩桩位优化问题时，其主要存在如下问题:①引入的简化假定与实际的抗滑桩的受力、位移等情况不符;②不同的假定滑动面情况下，抗滑桩的合理受力形式并没有明确地给出;③对于事先假定的滑动面的选择和岩土条块的划分目前尚没有统一的标准。但由于极限平衡法原理简单，且求解出的结果满足工程应用的要求，因此该方法目前仍是实际工程中研究抗滑桩桩位优化问题的常用方法。

2．2 极限分析法

除了运用极限平衡法之外，很多研究者采用了极限分析法来进行抗滑桩边坡加固工程的优化。如Ausilio等［33］通过运动学的极限分析法，分析了用抗滑桩加固土质边坡的稳定性，研究结果表明:抗滑桩的最优布设位置在近坡脚处，在稳定系数相同的情况下，此时抗滑桩的受力取得最小值，此外当抗滑桩布设在边坡中部到坡脚范围内时，抗滑桩对稳定边坡更有效;Nian等［34］通过极限分析得出:抗滑桩的最优布设位置位于边坡的坡脚处，此时抗滑桩在满足相同稳定安全系数的条件下受力最小;Li等［18］运用极限分析上限定理和Ito等［12］提出的塑性理论来计算抗滑桩提供的水平向抗滑力，并对抗滑桩的合理布设位置进行了研究，并指出:当抗滑桩提供的抗滑力足够大时，最有效的布设位置是靠近坡顶的位置，而考虑抗滑桩能提供的抗滑力与所需提供的抗滑力的关系时，最合适的布设位置与设计的稳定安全系数有关，最安全的布设位置是边坡的中上部区域;Li等［35］考虑抗滑桩加固边坡的土拱效应和强度折减技术，运用极限分析法对堆积层滑坡中抗滑桩的合理布设范围进行了研究，结果表明:抗滑桩的布设存在一个合理的布设范围，在同一截面上，根据桩的受力情况，抗滑桩布设应从中间向两边由密到疏。

目前运用极限分析法研究抗滑桩桩位优化问题时，其主要存在如下问题:①计算求解过程复杂，有时上、下限法得出的上、下限解相差太大，影响实际工程运用可信度;②事先假定的滑动面的形态较少，且与实际滑面形态有差别;③目前尚很少考虑抗滑桩的滑面以下部分的受力等情况及其对桩位优化的影响。由于极限分析法假定边坡岩土体为理想弹塑性体，应满足小应变假设，因此该方法主要用于抗滑桩加固未明显滑动的边坡问题分析中。

2．3 有限元强度折减法

目前有限元强度折减法是比较常用的边坡稳定性分析方法，它通过不断降低岩土体抗剪强度参数，直至达到极限破坏状态，此时的强度折减系数就是稳定安全系数。如韦立德等［36］针对抗滑桩加固边坡的稳定性优化问题，釆用抗剪强度折减弹塑性有限元法进行了研究，结果表明:在坡脚和坡顶水平且岩土体材料是各向同性的边坡中，如釆用单排抗滑桩加固，则抗滑桩布设在边坡中部时最有利于提高边坡的稳定性，且增大抗滑桩的密度比增大桩径更能有效地提高边坡稳定性;雷文杰等［37］采用有限元强度折减法对单排桩、桩间距为4 m的抗滑桩加固滑坡的桩位进行了数值模拟研究，结果表明:当抗滑桩设置在不同的位置时，滑坡的稳定安全系数是不同的，滑动面的位置和形状也相差各异;在稳定安全系数相同的情况下，当抗滑桩位于斜坡中部时所受的滑坡推力、内力最大，从经济角度出发，在中部设置抗滑桩是不合理的;抗滑桩设置在斜坡中部时的稳定安全系数最高，靠近两端时斜坡的稳定安全系数变化规律大致相同;当抗滑桩设置在斜坡中下部时，滑动面为在桩顶或斜坡上部某位置越顶滑出，当抗滑桩设置在斜坡上部时，滑动面沿桩前土体滑出;谭捍华等［38］基于强度折减技术和岩土塑性极限分析理论，从能量法的角度研究了岩土边坡抗滑桩加固位置、桩长和多抗滑桩共同加固边坡的分析方法，结果表明:抗滑桩布设位置的改变对边坡稳定安全系数、临界滑裂面位置和桩长均有显著影响，抗滑桩加固边坡的最优布设位置应位于边坡中下部区域;邹盛堂等［39］采用弹塑性有限元强度折减法对抗滑桩加固土坡进行了三维数值模拟分析，并且考虑了桩-土相互作用，研究了边坡潜在危险滑动面和稳定性系数与抗滑桩桩位的关系，结果表明:对于均质土坡，在滑面未知的情况时抗滑桩宜设置于边坡中部偏下［39］。

运用有限元强度折减法研究抗滑桩桩位优化问题时，其存在的主要问题是评价抗滑桩加固边坡后的塑性破坏的指标目前尚不统一，对于非连续介质问题该法不太适用，但相对前两种理论计算方法，该方法由于不需要事先假定滑面形态，且较好地考虑了岩土体的真实应力-应变状态，因此仍是常用的边坡稳定性分析方法之一。

2．4 数值模拟法

Cai等［40］通过三维有限元软件分析得出:抗滑桩应布设在坡体中部位置，以获得最大的稳定安全系数;Bellezza等［41］分析了被单排抗滑柱加固的双层土质边坡的稳定性，结果表明:在不同的土体抗剪强度情况下，边坡稳定性分析桩位也不同，最优桩位即是加固边坡取得最大稳定安全系数的位置;Won等［42］通过有限差分法FLAC3D软件分析得出:当抗滑桩布设于边坡中部时，作用在桩上的压力取得最大值，同时抗滑桩加固的边坡也可以取得最大的稳定安全系数;夏永成［43］对抗滑桩的合理位置运用ABAQUS软件和Geoslope软件进行了分析，结果表明:抗滑桩加固边坡能有效地提高边坡的稳定安全系数，在边坡中部附近设置抗滑桩能使加固后的边坡稳定安全系数达到最大;Wei等［44］通过运用FLAC3D软件对单排桩加固的边坡进行了分析，在桩距很短时将边坡的临界滑动面分成了两部分，结果表明:随着桩距的增长，临界滑动面渐渐清晰地形成;边坡中单排桩的最优桩位在边坡中部和临界滑动面中部之间;董必昌等［45］提出一种对边坡进行有限元分析，找出位移最大的位置，在此设置抗滑桩并进行配筋设计的抗滑桩优化设计方法，经工程实例验证该方法所得结果相对传统配筋设计方法更合理;Li等［46］利用FLAC2D软件对单排桩桩位及其分布对边坡稳定性的影响进行了评估，并将数值分析结果与简化Bishop法等进行了比较，结果表明:桩土相互作用显著地影响了边坡稳定性，当抗滑桩位于边坡的中部时可以取得最大的稳定安全系数，即最优桩位;年廷凯等［47］采用强度折减有限元程序通过三维数值模拟研究了抗滑桩-边坡体系的计算模型尺度、设桩位置等对边坡稳定性的影响，结果表明:抗滑桩的最安全位置为边坡中部。

运用数值模拟法研究抗滑桩位优化问题时，可以较直观地展示岩土体与桩的应力、位移等情况和滑动面的形成发展过程，并可以对所研究的问题通过数值模拟验证理论计算的结果;但该方法的缺点是不能很好地考虑抗滑桩与边坡岩土体的相互作用，且计算结果的精度依赖于数值计算技术。

2．5 物理模型试验法

高长胜等［48］通过离心模型试验对不同桩位与桩头条件下釆用抗滑桩加固边坡的变形破坏特性进行了研究，结果表明:抗滑桩设在边坡中部以及桩头固定情况下对边坡土体的遮挡效果最佳，同时边坡的稳定安全系数可达到最大值;李荣建等［49］通过室内模型试验研究了在地震作用下不同加固位置的抗滑桩的动力响应和边坡变形情况，结果表明:采取较高的加固位置可以有效地发挥抗滑桩的抗弯承载能力，并有利于抑制坡顶沉降和坡顶建筑物的稳定;虽然加固于边坡中部的抗滑桩承载能力发挥略小，但对抑制坡底变形和防止局部失稳有明显促进作用，从而能有效地保护边坡底部建筑物;杨光华等［50］通过室内物理模型试验对推移式、牵引式和复合式三种形式滑坡进行了分析，研究了不同桩位的稳定安全系数的大小与坡体应力场和位移场的关系，结果表明:推移式滑坡的最优桩位在坡体的上部，牵引式滑坡的最优桩位在坡体下部，复合型滑坡的最优桩位在坡内应力水平和位移较大的位置上;徐骏等［51］采用室内模型试验方法对已知滑面的折线形滑坡的双排桩推力分担规律进行了研究，并指出改变桩排间距、桩顶埋深能有效地改善双排桩滑坡推力分担比例［51］。

运用物理模型试验法研究抗滑桩桩位优化问题，物理模型与实际的工况具有很好的可比性，可以更好地考虑桩与土的作用，且具有时效性，因此可采用此方法对理论计算和数值模拟的结果进行验证，但应用该法时需考虑尺寸效应的影响。

3 存在的问题及研究展望

综上所述，对于抗滑桩加固边坡后的稳定性研究成果较多，研究方法主要有极限平衡法、极限分析法、强度折减法、数值模拟法和物理模型试验法。然而针对抗滑桩的合理桩位优化问题，虽然许多学者采用了许多方法从多方面进行了研究，但总的来说尚未形成一个完整的体系，本文认为还应该从以下方面进行更深入的研究:

(1)在抗滑桩边坡加固工程中，很多理论都是基于抗滑桩是完全刚性或其承载力足够大，但实际工程中抗滑桩并不是完全刚性的，并且其承载能力有限，因此在进行抗滑桩边坡加固工程中有必要考虑桩体本身的性质。

(2)目前对抗滑桩的桩位优化问题研究大多数只是集中于单排桩加固边坡的情况，然而实际上对于大型边坡，如果单排桩加固后仍不能满足安全的要求，则需要对其进行双排桩加固，但实际工程中已广泛采用的双排桩甚至多排桩加固边坡的桩位优化问题尚未进行深入研究，因此对双排桩或多排桩边坡加固工程进行研究，则更符合实际工程情况。

(3)针对不同几何形态的的边坡加固工程，抗滑桩布设桩位优化问题的研究较少，实际工程中的边坡形状变化较大，并不单一，而目前针对此类边坡抗滑桩的桩位优化研究的理论知识还不够成熟，有待深入研究。

(4)在地震频发的地区，地震对边坡会产生显著的破坏效应，降低边坡的稳定性，给工程建筑带来安全隐患，而目前关于地震作用下抗滑桩的桩位优化研究较少，对该方面的研究将具有重要意义。

(5)目前对于抗滑桩加固工程的研究没有考虑岩床的多层性，而实际工程中岩床可能是多层，如三峡地区侏罗系地层为软硬夹层，研究抗滑桩桩位优化时如果能考虑下伏岩床的岩性及岩层夹层，则会更具有工程实践应用价值。

［1］Li X P，He S M，Wang C H．Stability analysis of slopes reinforced with piles using limit analysis method［J］．Journal of Neural Engineering，2014，9(151):105-112．

［2］郑颖人，陈祖煜，王恭先，等．边坡与滑坡工程治理［M］．北京:人民交通出版社，2007．

［3］Fellenius W．Calculation of stability of earth dams［C］//Trans．2nd Cong．on Large Dams．Washington D．C．，1936，4:445-459．

［4］Bishop A W．The use of the slip circle in the stability analysis of slops［J］．Géotechnique，1955，5(1):7-17．

［5］Morgenstern N R，Price V E．The analysis of the stability of general slip surfaces［J］．Géotechnique，1965，15(1):79-93．

［6］Spencer E．A method of analysis of the stability of embankments assuming parallel inter-slice forces［J］．Géotechnique，1967，17(1): 11-26．

［7］Spencer E．Thrust line criterion in embankment stability analysis［J］．Géotechnique，1973，23(1):85-100．

［8］Sarma S K．Stability analysis of embankments and slopes［J］．Géotechnique，1973，23(3):423-433．

［9］Janbu N．Slope stability computation［M］//Hirschfield R C，Poulos S J．Embankment-dam Engineering．New York:John Wiley＆Sons，Incorporated，1973:47-86．

［10］钱家欢，殷宗泽．土工原理与计算［M］．北京:中国水利水电出版社，1996．

［11］铁道部第二勘测设计院．抗滑桩设计与计算［M］．北京:中国铁道出版社，1983．

［12］Ito T，Matsui T．Methods to estimate lateral force acting on stabilizing piles［J］．Soils and Foundations，1975，15(4):43-59．

［13］Ito T，Matsui T，Hong W P．Design method for the stability analysis of the slope with landing pier［J］．Soils and Foundations，1979，19 (4):43-57．

［14］穆启超，王万迁，蔡铁刚．四川地震灾区某滑坡稳定性分析及治理工程方案比选［J］．安全与环境工程，2011，18(4):11-16．

［15］何丹．边(滑)坡加固的抗滑桩桩位优化分析［D］．武汉:武汉理工大学，2013．

［16］汪承亮．极限分析法在边坡稳定分析及挡土墙土压力计算中的应用［D］．合肥:合肥工业大学，2010．

［17］Chen W F．Limit Analysis and Soil Plasticity［M］．Amsterdam: Elsevier Science，1975．

［18］Li X P，Pei X J，Gutierrez M．Optimal location of piles in slope stabilization by limit analysis［J］．Acta Geotechnica，2012，7(3):253-259．

［19］Zienkiewicz O C，Humpheson C，Lewis R W．Associated and non-associated visco-plasticity and plasticity in soil mechanics［J］．Géotechnique，1975，25(4):671-689．

［20］Ugai K．A method of calculation of total safety factor of slope by elasto-plastic FEM［J］．Soils and Foundations，1989，29(2):190-195．

［21］宋二祥．土工结构安全系数的有限元计算［J］．岩土工程学报，1997，19(2):1-7．

［22］郑宏，李春光，李焯芬，等．求解安全系数的有限元法［J］．岩土工程学报，2002，24(5):626-628．

［23］邵安东．用强度折减法对抗滑桩支护边坡的优化分析［D］．北京:北京交通大学，2009．

［24］戎斌斌．边坡抗滑桩空间优化布置与安全监测［D］．杭州:浙江大学，2010．

［25］Reddish D J，Ellis E A，Durrani I K．Numerical modelling of discrete pile rows for slope stability and generic guidance for design［J］．Géotechnique，2010，60(3):185-195．

［26］余小马．滑坡治理中抗滑桩设计有关问题的探讨［J］．城市勘测，2003，(1):15-21．

［27］张涛，门玉明，石胜伟，等．悬臂式单锚抗滑桩加固黄土滑坡的模型试验［J］．安全与环境工程，2015，22(3):151-157．

［28］Poulos H G．Design of reinforcing piles to increase slope stability［J］．Canada Geotech，1995，32(5):808-818．

［29］Lee C Y，Hull T S，Poulos H G．Simplified pile-slope stability analysis［J］．Computers and Geotechnics，1995，17(1):l-16．

［30］Hassiotis S，Chameau J L，Gunaratne M．Design method for stabilization of slopes with piles［J］．Journal of Geotechnical and Geoenvironmental Engineering，1997，123(4):314-323．

［31］王亮清，梁烨，唐辉明．一种确定抗滑桩桩位的方法一结构设计法［J］．铁道建筑，2004(10):64-65．

［32］李家平，赖允瑾，李永盛，等．利用抗滑桩加固临水坡岸的边坡稳定性分析水利［J］．水运工程学报，2005(2):53-58．

［33］Ausilio E，Conte E，Dente G．Stability analysis of slope reinforced with piles［J］．Computers and Geotechnics，2001，28(8):591-611．

［34］Nian T K，Chen G Q，Luan M T，et al．Limit analysis of the stability of slopes reinforced with piles against landslide in nonhomogeneous and anisotropic soils［J］．Canadian Geotechnical Journal，2008，45 (8):1092-1103．

［35］Li C D，Wu J J，Tang H M，et al．A novel optimal plane arrangement of stabilizing piles based on soil arching effect and stability limit for 3D colluvial landslides［J］．Engineering Geology，2015，195:236-247．

［36］韦立德，杨春和，高长胜．基于三维强度折减有限元的抗滑桩优化探讨［J］．岩土工程学报，2005，27(11):1350-1352．

［37］雷文杰，郑颖人，冯夏庭．滑坡治理中抗滑桩桩位分析［J］．岩土力学，2006，27(6):950-954．

［38］谭捍华，赵炼恒，李亮，等．抗滑桩预加固边坡的能量分析方法［J］．岩土力学，2011(S2):190-197．

［39］邹盛堂，戴自航．抗滑桩加固土坡效果及合理桩位的三维有限元分析［J］．福州大学学报，2012，40(5):664-669．

［40］Cai F，Ugai K．Numerical analysis of the stability of a slope reinforced with piles［J］．Soils and Foundations，2000，40(1):73-84．

［41］Bellezza I，Pasqualini E．Parametric study of the stability of slopes reinforced with piles［C］//Proceedings of the16th International Conference on Soil Mechanics and Geotechnical Engineering，2005，76:1319-1322．

［42］Won J，You K，Jeong S，et al．Coupled effects in stability analysis of pile-slope systems［J］．Computers and Geotechnics，2005，32(4): 304-315．

［43］夏永成．考虑桩-土相互作用的抗滑桩加固边坡设计方法研究［D］．大连:大连理工大学，2006．

［44］Wei W B，Cheng Y M．Strength reduction analysis for slope reinforced with one row of piles［J］．Computers and Geotechnics，2009，36 (7):1176-1185．［45］董必昌，舒陶浪，安新强，等．边坡抗滑桩优化设计［J］．武汉理工大学学报(交通科学与工程版)，2010，34(6):1138-1140，1145．

［46］Li X P，He S M，Luo Y，et al．Numerical studies of the position of piles in slope stabilization［J］．Geomechanics＆Geoengineering，2011，6(3):209-215．

［47］年廷凯，徐海洋，刘红帅．抗滑桩加固边坡三维数值分析中的几个问题［J］．岩土力学，2012，33(8):2521-2526，2535．

［48］高长胜，魏汝龙，陈生水．抗滑桩加固边坡变形破坏特性离心模型试验研究［J］．岩土工程学报，2009，31(1):145-148．

［49］李荣建，于玉贞，李广信．土质边坡中部与项部抗滑桩动力响应和边坡变形比较［J］．山地学报，2010，28(2):135-140．

［50］杨光华，钟志辉，张玉成，等．根据应力场和位移场判断滑坡的破坏类型及最优加固位置确定［J］．岩石力学与工程学报，2012，31(9):1879-1887．

［51］徐骏，李安洪，肖世国．折线型滑面滑坡桩排推力分布规律研究［J］．岩土力学，2012，33(11):3479-3488．

Research Progress of the Stability Evaluation of Slope Reinforced with Stabilizing Piles and Optimization of Pile Location

SONG Yingjie，CHEN Wenqiang，LI Changdong
(Faculty of Engineering，China University of Geosciences，Wuhan430074，China)

The collapse of slope is a common geological problem greatly affecting the safety of human engineering construction activity．One of the most commonly used prevention and control measures in slope treatment projects is stabilizing piles．However，there has been few researches on the evaluation of slopes reinforced with piles so far．This paper is to summarize and analyze the researches on stability evaluation of slopes reinforced with piles and optimization of the location for stabilizing piles．The paper mainly reviews the approaches of stability analysis of slopes reinforced with stabilizing piles in the achievements in theoretical calculation，numerical simulation and physical tests and compares their advantages and disadvantages．Then the paper summarizes and analyzes the common methods of optimizing the stabilizing pile location and applicable conditions．At last，the paper points out the development direction for future research，which may provide reference for similar research in future．

slope;stabilizing pile;stability analysis;optimization of pile location

X43;P642．22;TU457

ADOI:10．13578/j．cnki．issn．1671-1556．2016．05．007

1671-1556(2016)05-0043-07

李长冬(1981—)，男，教授，博士生导师，主要从事岩土体稳定性评价与地质灾害防治方面的教学与科研工作。E-mail:lichang-dong2004@163．com

2016-05-31

2016-09-06

国家自然科学基金项目(41472261);中央高校基本科研业务费专项资金项目(腾飞计划)(CUG150621)

宋英杰(1993—)，男，本科生，主要研究方向为边坡防治。E-mail:13071257196@163．com