数形结合方法在概率论教学中的应用

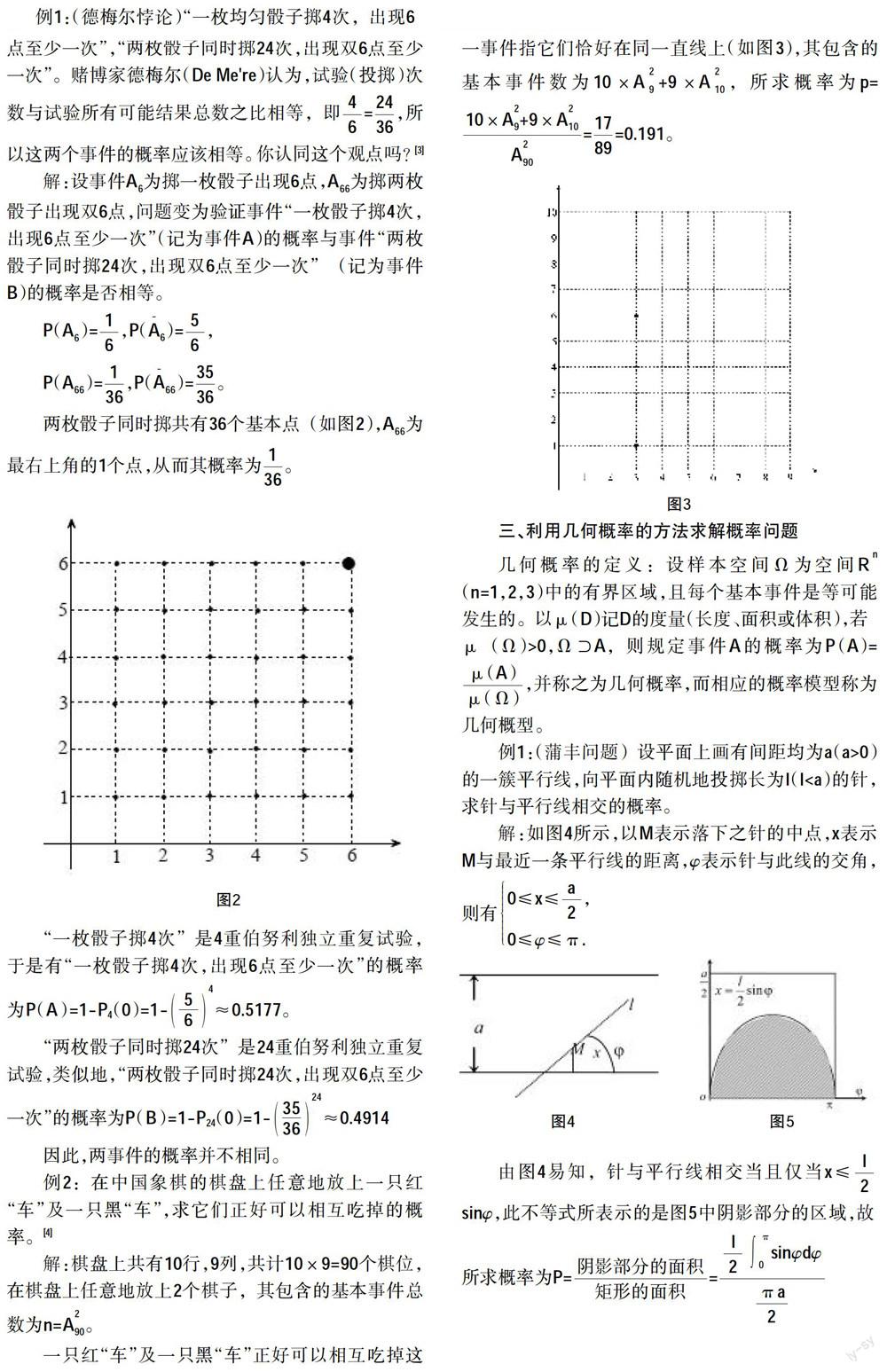
摘要：数形结合是一种非常有效的教学方法，解题时若能数形结合，可得到创新的解题方法和技巧。本文通过该方法在求解“概率”过程中的应用，加强了对概率的定义及定理的理解，有效的将抽象内容转变为具象形式，从而降低了学习难度，提高了学习效果。

关键词：数形结合；概率；应用

中图分类号：O212 文献标志码：A 文章编号：1674-9324（2016）12-0160-03

所谓数形结合，就是根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题的思想，实现数形结合。华罗庚教授曾对数形结合的思想做出了深刻、透彻的阐释：“数缺形，少直观；形缺数，难入微”。具体地说，就是在解决数学问题时，根据问题的背景，用联系的观点，根据数的结构特征，构造出与之相适应的图形，然后利用图形的性质和规律，解决“数”的问题；或将图形的部分信息或全部信息转化成“数”的信息，弱化或消除“形”的推理，从而将“形”的问题转化成数量关系来解决[1]。数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”，使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的。

数形结合是数学解题中常用的思想方法，数形结合的思想可以使某些抽象的数学问题直观化、生动化，能够变抽象思维为形象思维，有助于把握数学问题的本质。另外，由于使用了数形结合的方法，很多问题便迎刃而解且解法简捷。目前，数形结合思想在解相关的代数问题、几何问题中的应用已经受到人们的充分关注，并进行了较深入的讨论。其实数形结合在求解概率问题中也可有所作为，有时还会发现巧妙解法，取得事半功倍之效果[2]。

以下结合几个概率问题的求解，阐述数形结合在概率解题中的应用。

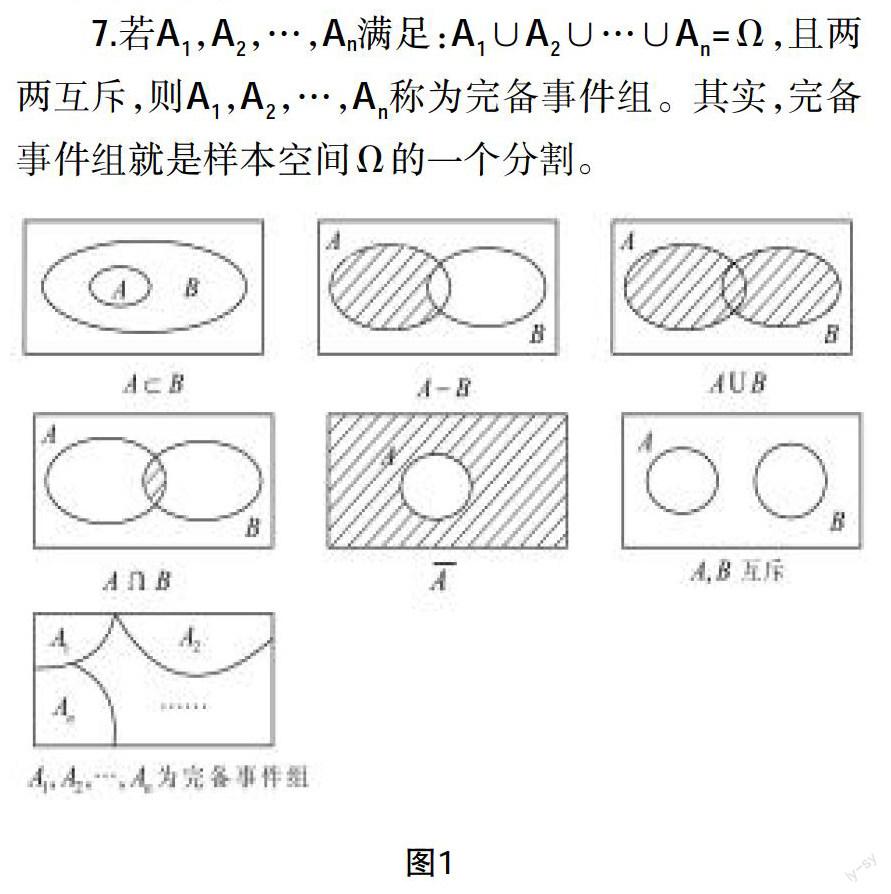
一、利用韦恩图法解决事件之间的关系问题

一般用“圆”或“椭圆”的图形来表示随机事件，利用韦恩图法能直观地解答有关事件之间的关系问题。下面的图形分别表示了事件间的如下关系：

1.若A？奂B，则A称为B的子事件，表示A发生必然导致B发生。

2.A-B称为A与B的差事件，A-B发生即A发生而B不发生。

3.A∪B称为A与B的和事件，A∪B发生当且仅当A，B中至少有一个发生。

4.A∩B称为A与B的积事件，简记作AB。AB发生的充要条件是A与B同时发生。

数形结合思想在概率论的教学中有着重要的地位，从上面所举的例子中可以看出：数形结合思想的“数”与“形”结合，相互渗透，把概率的精确刻画与几何图形的直观描述相结合，使概率问题与几何直观相互转化，使抽象思维和形象思维有机结合；应用数形结合思想，就是在充分考查概率问题的条件和结论之间的内在联系，将数量关系和空间形式巧妙结合来寻找解题思路，使问题得到顺利解决。无图不成书，无图不成课，只有充分把握概率论课程的特点，有效实施数形结合的教学方法，提高教学效率，才能让学生有效、高效地达到学习的目的和效果。

参考文献：

[1]李延奎.数形结合思想在解题中的应用[J].山东教育，2013，（27）.

[2]冯波，姜艳平.数形结合思想在解一类概率问题中的应用的例子[J].数学教学通讯，2004，（SC）.

[3]戴琳，陈秀华，秦叔明.概率论与数理统计[M].北京：高等教育出版社，2009.

[4]戴琳，秦叔明.概率论与数理统计学习指导[M].北京：高等教育出版社，2011.