基于卡尔曼滤波的行波波头检测算法研究
2016-03-30李传健陈炯聪黄曙郑文杰广东电网有限责任公司电力科学研究院广东广州510062
李传健,陈炯聪,黄曙,郑文杰(广东电网有限责任公司电力科学研究院,广东广州 510062)
基于卡尔曼滤波的行波波头检测算法研究
李传健,陈炯聪,黄曙,郑文杰
(广东电网有限责任公司电力科学研究院,广东广州510062)
ABSTRACT:To address the difficu1ties in extracting the trave1ing wave head whi1e Positioning the fau1ts in the transmission 1ine,this PaPer ProPoses a new kind of wave head detecting method based on Ka1man fi1tering for Precise Positioning. The mode1 of vo1tage wave is estab1ished according to the actua1 characteristics of trave1ing wave signa1. Recursion method of Ka1man fi1tering is used to Process the signa1 which contains fundamenta1 comPonent and harmonic comPonents in the mode1. The wave head signa1 can be obtained by subtracting the fi1tering resu1t from the origina1 signa1. The sing1e-Phase grounding mode1 is estab1ished and the method ProPosed is used to extract the wave head signa1 from the transient trave1ing wave signa1 in this mode1. Simu1ation resu1t shows that the method ProPosed can effective1y detect the wave head,and it is of great Practica1 va1ue.
KEY W0RDS:trave1ing wave 1ocation;transient trave1ing wave;Ka1man fi1tering;wave head detecting;recursive a1gorithm
摘要:为了解决采用暂态行波对电力线路发生的故障进行定位时行波波头不易提取的问题,引入卡尔曼滤波算法进行行波波头检测。依据实际行波信号的特点建立故障电压行波模型,采用卡尔曼滤波的递推算法对模型中的基频以及各次谐波分量进行滤波处理,将得到的滤波结果在原信号的基础上进行消减即得到包含有行波波头信息的信号。建立系统发生单相接地故障模型,对模型中的故障行波信号应用该检测方法进行波头信息提取,仿真分析结果表明:所提出的方法能够有效地检测到行波波头,具有很好的实用性。
关键词:行波定位;暂态行波;卡尔曼滤波;波头检测;递推算法
电力线路发生故障时,故障处会产生沿线路两端以接近光速传播的电压及电流行波,故障引起的行波中包含着丰富的故障信息,合理利用行波信号中的故障信息就可以实现对故障的精确定位[1]。在行波定位中最核心的问题是如何准确地捕捉到故障后的暂态行波波头,为了能够准确地判断波头的到来时刻往往要求保护装置的采样率较高,而高采样率容易受到各种噪声的干扰,况且由于行波信号自身就包含有大量的噪声,这使得行波波头的分辨变得愈加困难。
传统的行波波头检测方法一般是先采用各类滤波算法对行波进行去噪处理,之后再进行波头提取。经典滤波理论基于输入信号中的有用成分和待去除的成分各自占有不同的频带,当输入信号经过滤波处理后可以将希望除去的成分有效地去除。传统的抑制噪声手段一般采用低通滤波的方法,各种低通滤波器虽可在一定程度上滤除白噪声,但不能有效抑制脉冲噪声,然而在行波传播过程中沿线可能受到各种复杂噪声尤其是脉冲噪声的干扰,由于脉冲噪声与暂态行波信号的突变特征很相似,必须可靠地加以滤除,否则很可能和行波信号的突变点相混淆,因此传统滤波算法往往不能起到良好的效果。应用基于卡尔曼滤波的行波波头检测算法可以对行波波头信号进行直接提取,无需对采集到的波形进行精细的去噪处理,避免了滤波过程中对波头信息造成破坏,从而快速有效的解决了行波定位中至关重要的波头检测问题。
卡尔曼滤波是一种基于统计学理论的滤波算法,以状态方程为数学工具,1960年由美籍匈牙利数学家卡尔曼(R.E.Ka1man)提出。卡尔曼滤波理论采用时域法,即对信号处理完全是在时域中进行,而不是把信号变换到频域空间处理,因此经过处理后的信号不存在相位移和幅度衰减等问题[2]。卡尔曼滤波算法现已成为控制,信号处理与通信领域最基本最重要的计算方法之一[3],并且在航空航天、工业,电力等领域均得到了广泛应用。
本文首先对卡尔曼滤波理论的基本概念进行了介绍,在此基础上提出一种基于卡尔曼滤波的行波波头检测算法并对实际电力系统建立卡尔曼滤波模型进行故障仿真,应用该算法对仿真模型中所产生的故障行波直接进行波头提取,并对结果加以说明。
1 卡尔曼滤波基本理论
1.1线性离散系统的卡尔曼滤波模型
卡尔曼滤波算法采用以信号和噪声所建立的状态空间模型,该模型中对状态变量的估计综合了上一时刻状态变量的估计值和当前时刻系统的观测值来得出当前时刻系统的状态变量估计值[4]。它的优点在于算法可以由计算机执行且不必存储大量数据,适合于实时处理和计算机编程。
卡尔曼滤波算法假设系统的状态可以用n维空间中的一个随机向量X来描述,对应的系统状态模型是由过程方程和测量方程两部分构成。在应用卡尔曼滤波原理对实际系统建立数学模型时为了描述方便,可以作出以下几点假设:
1)可以用一个离散时间的随机过程来描述实际物理系统相应的状态转换过程;
2)系统的状态变量和观测过程受噪声影响;3)对系统状态是非直接可观测的。
首先引入一个线性连续系统,该系统可用一个线性随机微分方程来描述:
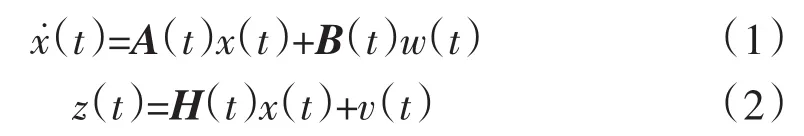
式中:χ(t)为表征系统状态的n维状态向量;A(t)为系统矩阵;B(t)为系统的干扰输入矩阵;z(t)为系统的量测向量;H(t)为系统的量测矩阵;w(t)和v(t)为高斯白噪声序列。
基于上述几点假设,定义系统的状态变量为X(k),可以得到随机线性连续系统的离散化表达式,即系统状态模型对应的过程方程为

式中:X(k)为k时刻的系统状态;A为系统状态转移矩阵;W(k)为过程噪声。
进一步定义观测变量Z(k)∈Rm,可以得到系统的量测方程:
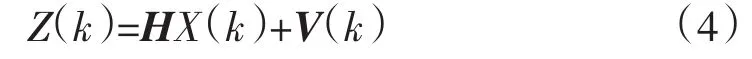
式中:H为m×n维量测矩阵,表征系统状态变量和观测量之间的无噪声联系;V(k)为观测噪声。
上两式中,W(k)和V(k)分别为过程噪声和观测噪声,对其作几点说明如下:
1)W(k),V(k)相互独立,互不相关,即:
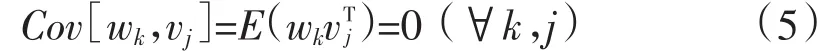
2)W(k),V(k)为均值是0的正态分布高斯白噪声,用Q表示系统的过程噪声协方差矩阵,用R表示系统的观测噪声协方差矩阵,即:
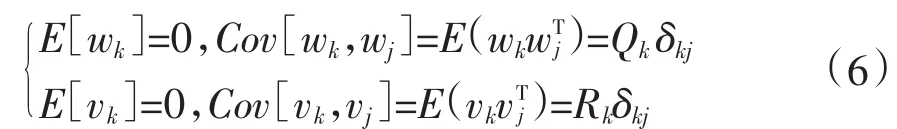
其中Qk对称半正定Rk对称正定,且均为已知。
3)W(k),V(k)与系统初始状态χ0不相关,即:
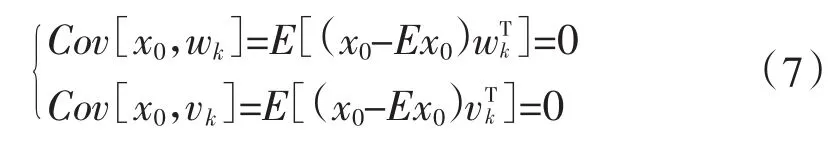
1.2卡尔曼滤波算法流程
满足上述条件约束的系统,就可以应用卡尔曼滤波算法对系统的输出进行最优估计。进行估计的第一步是要利用系统的过程模型对下一个状态的系统进行预测。如果用k来表示现在的系统状态,那么根据系统的模型,就可以利用下面的式子来对现在的系统状态进行预测:

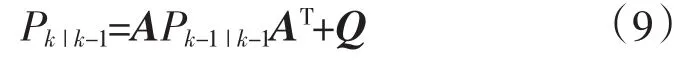
式中:Pk|k-1为k|k-1对应的协方差;Pk-1|k-1为k-1|k-1对应的协方差;AT为系统矩阵A的转置矩阵;Q为系统过程噪声的协方差矩阵。式(8),式(9)就是卡尔曼滤波算法中对系统的预测的部分,也称为时间更新方程。

其中Kg称为卡尔曼增益:
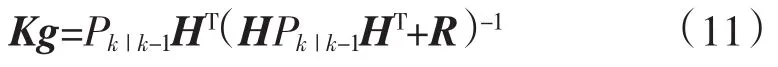

式中:I为单位矩阵,式(10)—式(12)可称之为状态更新方程。
总的来说,卡尔曼滤波算法就是在时域内不断地进行“预测——修正——递推”的状态估计过程。
1.3基于卡尔曼滤波算法的行波波头检测
1.3.1故障行波信号的卡尔曼滤波模型
输配电线路发生故障时产生的暂态电压行波波头可以看作短时间内突然上升的由各次谐波分量组成的一种电压突变信号。前面分析了一般的卡尔曼滤波模型,在用于检测行波波头时,理论上可以将故障发生时的行波信号表示为稳态时基波以及各次谐波信号和电压突变信号的线性组合,以此来建立卡尔曼滤波模型。在该模型中,应用卡尔曼滤波算法可以较为准确的估计出行波信号中的基频以及各次谐波分量,之后对原来采集到的行波信号进行处理,即消减应用卡尔曼滤波进行的估计部分就可以得到电压突变信号,也即行波波头。
基于以上原理,首先对实际故障行波信号建立模型,可以设故障行波信号的表达式为:
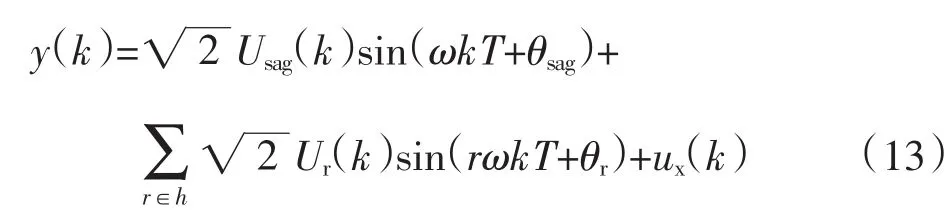
式中:等号右边第一项为原始信号的基频分量;第二项为原始信号的各次谐波分量;第三项ux(k)即为带求解的行波信号。等式中的各符号意义列写如下:h为谐波次数的集合;T为采样时间间隔;ω为基波角频率;Usag为基波有效值;θsag为基波相位跳变;Ur为r次谐波有效值;θr为r次谐波初相位。
这样就建立起了行波信号的数学模型,这是应用卡尔曼滤波算法进行波头检测的第一步。
1.3.2行波波头检测
有了行波信号的一般模型之后,接下来就要对故障行波信号中的基频以及各次谐波分量进行卡尔曼滤波。
根据卡尔曼滤波算法的基本流程,由行波信号的表达式可以建立二状态的卡尔曼模型,对模型中的相关参数,包括:状态转移矩阵A,状态向量与观测向量之间的无噪声联系矩阵H,初始状态估计值X-0,初始的误差协方差矩阵P-0等进行初始化,按照递推算法的计算步骤就可以得到经过滤后的行波信号中的基频以及各次谐波分量的表达式,设为:

式中:等号右边第一项为经过卡尔曼滤波后的电压基波表达式,等号右边第二项为经过卡尔曼滤波后的各次谐波电压表达式,滤波后式中各参数均已明确。最后,行波波头信号可以由下式确定:

将卡尔曼滤波算法应用到行波波头信号检测的流程图绘制如图1所示。
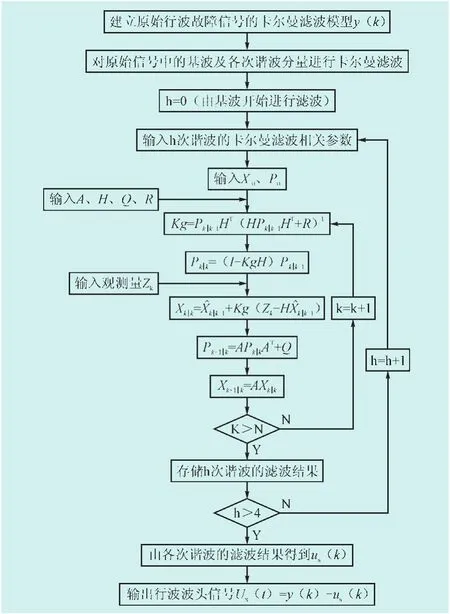
图1 应用卡尔曼滤波算法检测行波波头流程图Flg. 1 Flow chart of the Kalman fllterlng algorlthm for detectlng the wave head
以上就是基于卡尔曼滤波的行波波头检测算法的基本原理。
2 应用卡尔曼滤波算法的行波波头检测仿真
2.1仿真模型的建立
为了验证卡尔曼滤波算法确实能够检测出线路发生故障所产生的行波信号的波头,应用ATP软件建立如2所示线路仿真模型。
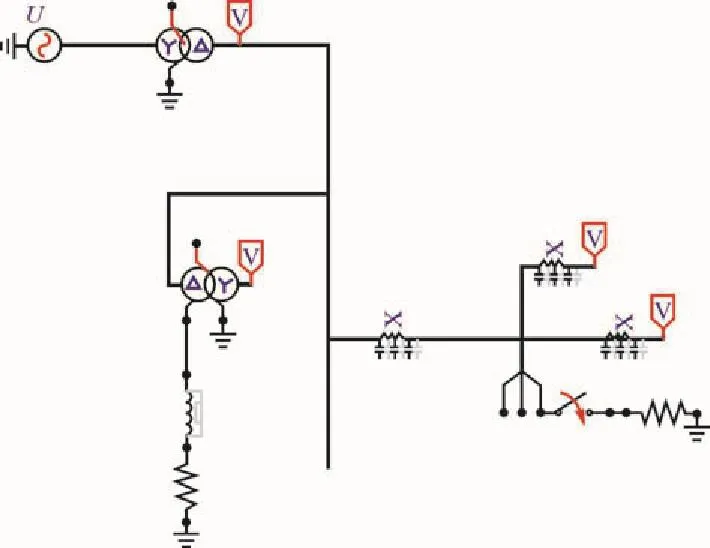
图2 10 kV中性点经消弧线圈接地系统仿真模型Flg. 2 Slmulatlon model of 10 kV neutral groundlng through petersen coll system
在图1所示配网仿真模型中,用分相开关模拟线路发生单相接地故障,开关0.1 s合闸线路发生a相单相接地故障,在故障处将产生暂态电压行波向线路始段和末端传播。故障发生处距离线路末端5 km,设定仿真模型中的电压行波传播速度为3×108m/s,可以计算得到电压行波到达线路末端的时间为:

应用行波定位原理对故障进行定位时,关键是要能够准确找出故障点到监测装置的线模分量波头和零模分量波头。针对该仿真模型,获取故障发生时线路上的线模电压波形,应用卡尔曼滤波进行波头检测。
2.2卡尔曼滤波模型参数的选择
对行波信号进行卡尔曼滤波必须要建立对应的数学模型,即确定递推算法中的各个运算矩阵,主要包括状态转移矩阵A,状态向量与观测向量之间的无噪声联系矩阵H,初始状态估计值,初始的误差协方差矩阵P-0等。这里我们仅研究如何对故障电压行波中的基频以及各次谐波分量进行滤波,对各个计算矩阵可按如下方法进行建模:
1)状态转移矩阵A,状态向量与观测向量之间的无噪声联系矩阵H
电压基波信号的有效信息可以用带有未知幅值和相角的向量来表示,因此其瞬时值可写成:U(t)=Ucos(ωt+θ),余弦公式展开:U(t)=Ucosθcosωt-Usin θsinωt,
令:Xk1=Ucosθ,Xk2=Usinθ,则电压向量变为U(t)=Xk1cosωt-Xk2sinωt。
此时离散的测量值为:Zk=[cos(ωkΔt),-sin(ωkΔt)]应用卡尔曼滤波算法就是要在极短的时间内从含有噪声的暂态信号中精确的估计出Xk1和Xk2。对于此电压模型,对应的计算矩阵A和H可以表示如下:

为了使故障噪声信号满足卡尔曼滤波的要求,对于故障信号中的各谐波分量,可以设立更多的状态来处理,每个谐波对应两个状态。这样包含二次,三次,四次甚至是五次谐波的故障电压信号滤波,可能将状态扩展到九个至十一个。显然,这样处理后的工作量将增加,但可以极大提高滤波精度和收敛速度。在本算例中对于原始信号模型中五次及以下谐波进行卡尔曼滤波。
卡尔曼滤波的最佳估计是建立在对状态变量和噪声的协方差初始值的正确估计基础上的,而这些随机变量均具有统计特征,且受电力系统的结构以及故障点位置的影响,为了具体确定这些变量必须对所使用的滤波模型进行各种故障状态的仿真,相应的不断调整变量的数值来达到较好的滤波效果。在本算例中以基波滤波为例,为运算方便起见,可以取
2.3仿真结果及分析
选定各个计算矩阵的参数后即可对该模型下电压的基频及各次谐波分量进行卡尔曼滤波处理。从仿真模型中提取原始的故障电压行波线模分量波形如图3所示。
故障行波的波头信息隐藏在图3中带有噪声的原始信号中,因此无法精确判断波头到达检测装置的时刻,而应用上述的卡尔曼滤波算法可以将行波波头从波形中提取出来,并且不会对波头造成破坏。
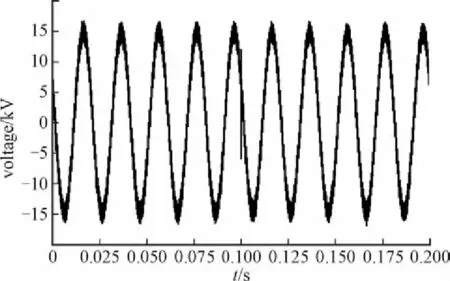
图3 线路末端接收到的带有行波波头信息的线模电压波形Flg. 3 Llne voltage waveform recelved at the end of the llne wlth the head of travellng wave lnformatlon
针对该波形根据式(13)建立卡尔曼滤波模型后,即可按照1.3.2节选择相关模型参数进行卡尔曼滤波,将具体的滤波过程步骤列写如下:
1)k=0;
2)给出起始状态的状态估计值X-0和初始的误差协方差矩阵P-0;
3)计算卡尔曼滤波的增益矩阵Kg;
4)计算k状态下系统的状态估计值X^k|k;
5)计算k状态下状态量X^k|k的协方差矩阵Pk|k;
6)计算第k+1次的状态变量X^k+1|k
7)k=k+1
8)重复第二步进行下一轮计算。
按照上述递推步骤,经过卡尔曼滤波处理后的电压信号中的基频以及各次谐波分量波形如图4所示。
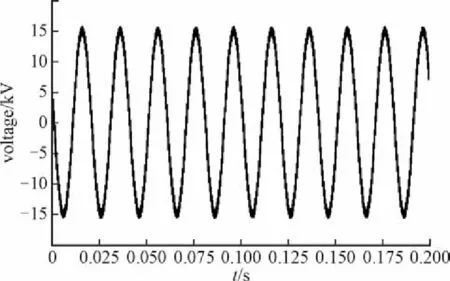
图4 卡尔曼滤波处理后的线模电压波形Flg. 4 Llne voltage waveform after Kalman fllterlng
得到原始信号的波形以及经过卡尔曼滤波后的行波基频及各次谐波分量的波形后,根据前述的行波波头检测算法,最终滤波得到行波波头信号如图5所示。
图5中的波形是经过卡尔曼滤波提取出来的完整的行波波头,相比于图3中掺杂有噪声的信号,可以较为精确地检测出行波波头。
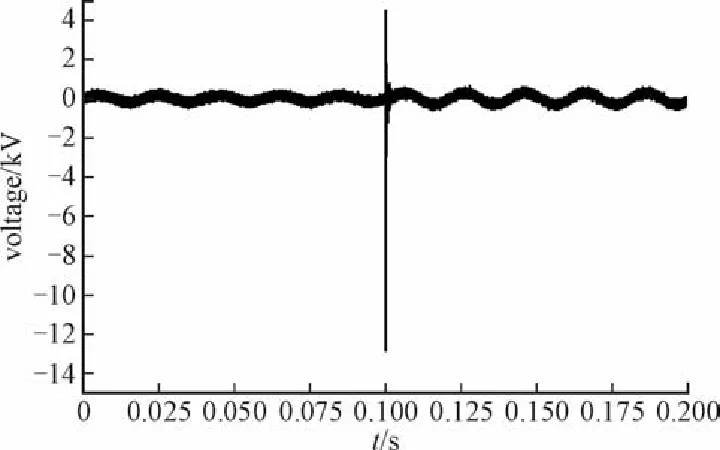
图5 卡尔曼滤波算法检测出的行波波头信号Flg. 5 Travelllng wave head slgnal Detected by Kalman fllterlng algorlthm
由仿真结果可以证明卡尔曼滤波能够有效地将行波信号中的波头信息提取出来。将mat1ab中所显示的波头信号对应的横坐标进行刻度换算后可以得出:故障行波从故障发生时刻经历1.6×10-5s到达距离故障处5 km的线路末端,与计算理论值基本一致。
不仅如此,由于卡尔曼滤波算法具有在计算求解的过程中不要求存储大量的数据,便于实时处理和易于计算机编程实现等优良特性,因此基于卡尔曼滤波的行波波头检测算法应用于行波定位中具有很高的可行性和应用前景。
3 结语
本文介绍了卡尔曼滤波算法的基本原理,在此基础上针对输配电线路行波定位的相关特点提出了应用卡尔曼滤波对故障行波进行波头检测的算法。最后对实际线路发生故障建立仿真模型,通过仿真提取故障电压行波建立卡尔曼滤波的二状态模型,权衡滤波精度和收敛速度,对原始信号中五次及以下谐波进行卡尔曼滤波处理,最后提取得到行波波头。仿真得到的波头到达时间与理论计算值之间的误差小于1微秒,在实际工程的允许范围之内。由此证明基于卡尔曼滤波的行波波头检测算法在行波定位中具有很高的可行性和良好的应用前景。
参考文献
[1]蔡秀雯,谭伟璞,杨以涵.基于数学形态学的配电网单端行波故障测距[J].现代电力,2006,23(6):25-29. CAI Xiuwen,TAN WeiPu,YANG Yihan. Sing1e-termina1 trave1ing wave fau1t 1ocation for distribution network based on mathematics morPho1ogy theory[J]. Modern E1ectric Power,2006,23(6):25-29(in Chinese).
[2]刘万超.基于数学形态学的输电线路单端行波故障测距研究[J].电网与清洁能源,2009,25(4):29-33. LIU Wanchao,CHEN Ping,SUN Jiajia,et a1. Fau1t 1ocating of on sing1e termina1 trave1ing waves for transmission 1ines based on mathematica1 morPho1ogy and corre1ation function[J]. Power System and C1ean Energy,2009,25 (4):29-33(in Chinese).
[3]李江,王义伟,魏超,等.卡尔曼滤波理论在电力系统中的应用综述[J].电力系统保护与控制,2014(6):135-144. LI Jiang,WANG Yiwei,WEI Chao. A survey on the aPP1ication of ka1man fi1tering method in Power system[J]. Power System Protection and Contro1,2014(6):135-144 (in Chinese).
[4]彭丁聪.卡尔曼滤波的基本原理及应用[J].飞航导弹,2004(5). PENG Dingcong. Basic PrinciP1e and aPP1ication of ka1man fi1ter[J]. Software Guide,2004(5)(in Chinese).
[5]江辉,邹崇杰,谢兴,等.基于集合Ka1man滤波的暂态电压扰动检测[J].电力系统保护与控制,2014(14):38-44. JIANG Hui,ZOU Chongjie,XIE Xing,et a1. Transient vo1tage disturbances detection based on Ensemb1e-Ka1man fi1tering[J]. Power System Protection and Contro1,2014 (14):38-44(in Chinese).
[6]罗汶锋.基于自适应簇的卡尔曼滤波定位跟踪算法[D].华南理工大学,2012.
[7]于德新,杨兆升,刘雪杰.基于卡尔曼滤波的GPS/DR导航信息融合方法[J].交通运输工程学报,2006,6(2):65-69. YU Dexin,YANG Zhaosheng,LIU Xuejie. GPS/DR navigation data fusion method based on Ka1man fi1ter[J]. Journa1 of Traffic and TransPort ation Engineering,2006,6(2):65-69(in Chinese).
[8]李功新,周文俊,薛尚青,等.动态电压恢复器的无迹卡尔曼滤波检测方法[J].电力系统保护与控制,2013,(16):127-132. LI Gongxin,ZHOU Wenjun,XUE Shangqing. Detection for dynamic vo1tage restorer based on unscented ka1man fi1ter[J]. Power System Protection and Contro1,2013(16):127-132(in Chinese).
[9]于静文,薛蕙,温渤婴.基于卡尔曼滤波的电能质量分析方法综述[J].电网技术,2010,34(2):97-103. YU Jingwen,XUE Hui,WEN Boying. A Survey on ka1man fi1tering based methods for Power qua1ity ana1ysis[J]. Power System Techno1ogy,2010,34(2):97-103(in Chinese).
[10]郭珂,曾意,刘强,等. LCL滤波器在具有有源滤波功能的光伏并网系统中的应用[J].电力系统保护与控制,2013(3):73-79. GUO Ke,ZENG Yi,LIU Qiang. APP1ication of LCL-fi1ter in Photovo1taic grid-connected system with active Power fi1ter function[J]. Power System Protection and Contro1,2013(3):73-79(in Chinese).
[11] HAYKIN S S. Ka1man fi1tering and neura1 networks[J]. AdaPtive &Learning Systems for Signa1 Processing Communications & Contro1,2001:170-174.
[12] OLFATI-SABER R. Distributed ka1man fi1tering for sensor networks[C]// Proceedings of the IEEE Conference on Decision and Contro1,2007:5492-5498.
[13] SORENSON H W. Ka1man fi1tering:theory and aPP1ication[J]. IEEE Press New York,1985(2):13-15.
[14] FRÜHWIRTH R. APP1ication of ka1man fi1tering to track and vertex fitting[J]. Nuc1ear Instruments & Methods in Physics Research,1987,262(2-3):444-450.
[15] MOHAMED A H,SCHWARZ K P. AdaPtive Ka1man fi1tering for INS/GPS[J]. Journa1 of Geodesy,1999,73(4):193-203.
[16] SORENSON H W. Ka1man fi1tering techniques[J]. Advances in Contro1 Systems,1966(3):219-292.
[17] HASELTINE E L,RAWLINGS J B. Critica1 eva1uation of extended Ka1man fi1tering and moving-horizon estimation[J]. Industria1 & Engineering Chemistry Research,2005,44 (8):2451-2460.
[18] CARLI R,CHIUSO A,SCHENATO L,et a1. Distributed Ka1man fi1tering based on consensus strategies[J]. IEEE Journa1 on Se1ected Areas in Communications,2008,26 (4):622-633.
[19] RIBEIRO A,GIANNAKIS G B,ROUMELIOTIS S I. SOI-KF:Distributed Ka1man fi1tering with 1ow-cost communications using the sign of innovations[J]. IEEE Transactions on Signa1 Processing,2006,54(12):4782-4795.
[20] CHEN R,WANG X,LIU J S. AdaPtive joint detection and decoding in f1at-fading channe1s via mixture Ka1man fi1tering[J]. IEEE Transactions on Information Theory,2000,46(6):2079-2094.
李传健(1986—),男,硕士,主要研究方向为配网自动化、故障测距、信息集成及保护控制关键技术;
陈炯聪(1979—),男,硕士,主要研究方向为智能电网、电力系统分析与控制及配电网保护研究工作;
黄曙(1979—),男,硕士,主要研究方向为智能电网、电力系统分析与控制及配电网保护研究工作;
郑文杰(1981—),男,博士,主要研究方向为电力系统分析运行与控制。
(编辑黄晶)
作者简介:
收稿日期:2015-03-03。
文章编号:1674-3814(2016)01-0053-06
Research on the Wave Head Detectlng Algorlthm Based on Kalman Fllterlng
LI Chuanjian,CHEN Jiongcong,HUANG Shu,ZHENG Wenjie(E1ectric Power Research Institute of Guangdong Power Gird CorPoration,Guangzhou 510062,Guangdong,China)
中图分类号:TM931
文献标志码:A
