基于灵敏度分析的孤立电网频率控制方法

吴云亮，肖峥，廖思阳

(1.中国南方电网电力调度控制中心，广东广州510000；2.武汉供电设计院有限公司，湖北武汉430000；3.武汉大学电气工程学院，湖北武汉430000)

基于灵敏度分析的孤立电网频率控制方法

吴云亮1，肖峥2，廖思阳3

(1.中国南方电网电力调度控制中心，广东广州510000；2.武汉供电设计院有限公司，湖北武汉430000；3.武汉大学电气工程学院，湖北武汉430000)

利用实时仿真平台对某地区含高耗能电解铝负荷的孤立电网进行仿真研究，分析不同运行方式下系统的安稳控制策略，指出在极端情况下安稳控制策略动作后系统仍会存在不平衡功率，提出一种基于电压灵敏度分析的孤立电网频率控制方法，仿真结果验证了控制方法的有效性。

电压灵敏度；不平衡功率；孤立电网；频率控制

我国幅员辽阔，负荷中心和能源中心呈现明显的逆向分布特点。其中绝大部分能源集中在西部地区，而负荷中心主要在长三角，珠三角和京津唐地区，这种能源和负荷中心逆向分布的特点导致能源不能高效利用，目前主要通过特高压和超高压远距离输电解决这一问题，但实际上将负荷建立在能源中心同样可以缓解这一问题。

文中研究的孤立电网不同于传统意义上的孤立电网，是一个含大规模可再生能源的容量在百兆瓦级以上的企业级孤岛型电网。该孤立电网全年运行在孤岛模式下，与大电网没有电气联系。由于没有大电网提供稳定支撑，孤立电网系统本身的等效转动惯量很小，一旦发生功率扰动或者发生故障安稳装置动作后系统可能存在大量不平衡功率，如果系统的备用容量小于不平衡功率，那么孤立电网系统将不能稳定运行，甚至可能发生系统崩溃。

文中利用RTDS实时仿真平台对一个含1 800 MW火电、800 MW风电和1 400 MW电解铝负荷的孤立电网进行仿真研究，分析孤立电网系统在不同运行方式下的安稳控制策略，指出在极端情况下安稳控制策略动作后系统存在不平衡功率，并提出一种基于电压灵敏度分析的孤立电网频率控制方法。

1 灵敏度分析方法

1.1 灵敏度的定义

灵敏度表示所要研究网络中的因变量对网络中的自变量的敏感程度，一般指在线性时不变的网络中，网络函数T对网络中元器件参数X的敏感程度，用符号来表示，定义式〔1〕如下:

灵敏度数值的大小反映了网络函数受参数变量影响的大小，灵敏度值越大，网络函数受参数变量的影响越大，灵敏度值越小，网络函数受参数变量的影响越小。

灵敏度分析方法是一种重要的电力系统分析方法，广泛应用于电力系统的各个方面，主要用来研究电力系统的可控变量和状态变量之间的关系，获得因变量对自变量敏感度大小〔1－6〕。根据相应的灵敏度指标结果，可以为自变量的输入提供指导，进而能够控制因变量得到想要的输出结果，根据计算所得的灵敏度指标对系统采取相应的控制策略可以显著的提高系统的稳定裕度和经济指标〔6〕。

1.2 灵敏度矩阵的定义

灵敏度矩阵是在电力系统潮流方程的基础上推导出来的，并不是系统中各个节点灵敏度的简单组合，是雅克比矩阵的改进和变形。灵敏度矩阵的性质可以用来研究电力系统领域的许多实际问题〔6〕。通常，电力系统的潮流方程可以简单地表示为:

式中 x是状态变量，u是控制变量，对式 (2)进行全微分可得:

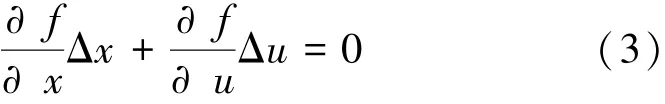
式 (3)为系统灵敏度方程的基本表达式，式中的矩阵∂f/∂x和∂f/∂u称为雅克比矩阵，当∂f/∂x非奇异时，状态变量偏差和控制变量偏差的线性关系式为:

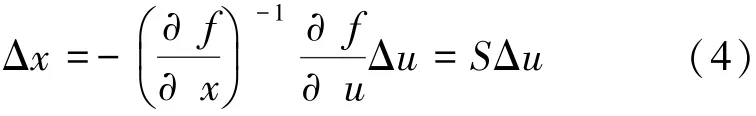
1.3 电压灵敏度分析的数学模型

电力系统在正常运行中，在较小的时间尺度上，各个节点电压幅值变化是成比例的〔7－9〕，即:

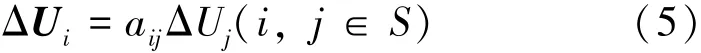
式 (5)中，S为系统中所有节点的集合，aij为ΔUi与ΔUj的灵敏度关系，其定义式如下:

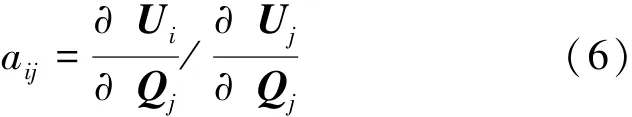
系统中各个节点之间的电气距离大小可以反映节点之间的电气联系的强弱。当2个节点之间开路时，电气距离为无穷远，当2个节点短路时，电气距离为0。节点之间的电气距离可以表示为:

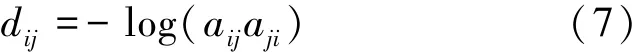
2 极端情况下的安稳控制策略及不平衡功率分析

文中的孤立电网与传统大电网和微电网有很大的不同，微小的扰动产生的不平衡功率可能导致系统崩溃。因此需要提前制定相应的安稳控制策略表。下面分析400 MW风电接入情况下 (不考虑风功率波动)系统N－1，N－2故障的安稳控制策略及产生的不平衡功率。

2.1 N－1故障不平衡功率分析

系统N－1故障后的安稳控制策略及不平衡功率如表1所示。根据表1可知，安稳控制策略动作后系统仍然存在不平衡功率，N－1故障后系统最大的功率缺额为150 MW，最小的功率缺额为－30 MW，因此最大不平衡功率为150 MW。

表1 系统N－1故障后的安稳控制策略及不平衡功率

2.2 考虑安稳控制策略的N－2故障不平衡功率分析

系统N－2故障后的安稳控制策略及不平衡功率如表2所示。

表2 孤立电网N－2故障后的安稳控制策略及产生的不平衡功率

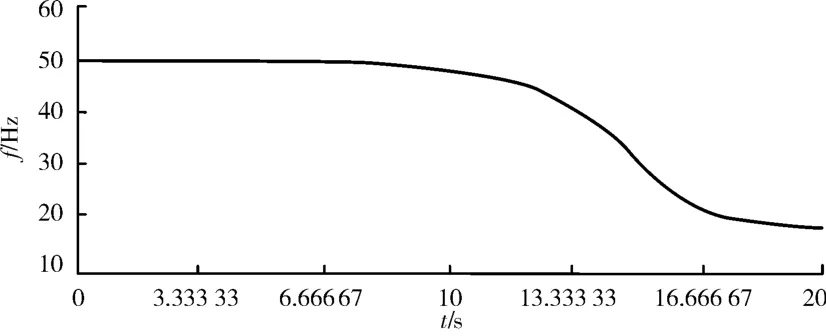
图1 系统的频率变化曲线

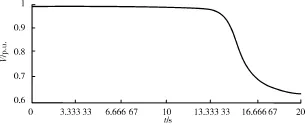
图2 系统的电压变化曲线

从图1和图2可以看出系统频率崩溃过程中，系统电压还能维持一段时间。因此系统出现不平衡功率的情况下首先考虑频率稳定控制。

3 基于电压灵敏度分析的孤立电网频率控制方法研究

根据表2知，N－2故障后系统最大的功率缺额为80 MW，最小的功率缺额为－130 MW，由于只考虑功率缺额为正值的情况，因此安稳控制策略后的N－2故障后的系统最大不平衡功率为80 MW。

2.3 极端情况下的不平衡功率的仿真分析

正常运行情况下，当火电机组出现故障停运后安稳控制策略动作的瞬间最大不平衡功率为150 MW，如果此时系统还有备用容量，那么孤立电网系统最终能够恢复到稳定运行状态。但是考虑特殊情况下，比如说有火电机组检修或者风电场输出风功率突减，再发生火电机组故障停运的话，此时产生的不平衡功率由于剩余所有火电机组可能都达到其机械功率输出极限，不能够参与一次调频，系统将发生崩溃事故，仿真结果如图1和图2所示。

3.1 不平衡功率的计算方法及分配方案

文中的孤立电网系统规模较小，在系统各个节点装设同步相角测量单元 (PMU)装置，可以建成广域测量系统 (WAMS)。PMU可以实现对全网同步相角和系统主要数据的实时高速采集，采集的数据通过PMU和快速通信网络实时传输到WAMS主站，从而能够对电力系统的正常运行情况和事故扰动情况进行实时监测和计算分析，并且能够及时掌握和获得电力系统的动态运行过程〔10－11〕。通过PMU可以实时获取系统的功率扰动大小和系统的有功调节容量，计算单元计算二者差值可得到系统的不平衡功率。

当系统的不平衡功率为正，即系统存在功率缺额的时候，系统的频率可能瞬间崩溃，导致系统崩溃。鉴于孤立电网系统的自调节能力较弱，考虑电解铝负荷具有一定的电压调节特性，因此系统通过降低电解铝负荷的电压来降低系统消耗的无功功率。在系统的不平衡功率ΔP已计算出来的情况下，可以按照三期电解铝负荷的权重计算每期电解铝负荷需要分别降低多少负荷，具体计算方案为，假设每期电解铝负荷消耗的有功功率为Pi(i＝1，2，3)需要降低的每期电解铝负荷的负荷权重为Ci，则每期电解铝负荷需要降低的有功功率ΔPi(i＝1，2，3)为

式中 C1＋C2＋C3＝1。

3.2 电解铝负荷节点电压的调整方法

研究电解铝负荷特性时，只考虑了整流负荷，4%的动力负荷忽略不计，根据IEEE负荷建模工作组推荐的参数〔12〕，整流负荷的幂函数形式的负荷特性关系式如下:

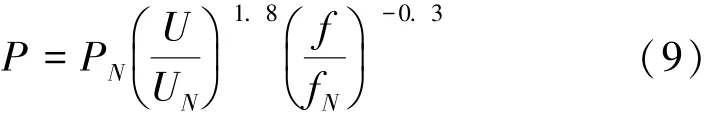
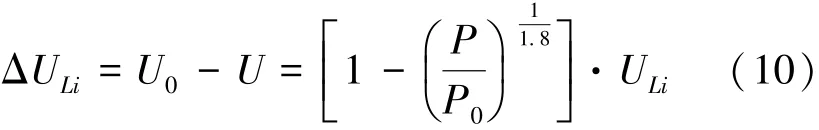
3.3 基于电压灵敏度的发电机节点电压的调整方法

电压灵敏度分析方法在电力系统中的应用一般采取离线决策、在线匹配的原则，即在某种稳定运行方式下可以计算出孤立电网系统的电压的灵敏度矩阵和电气距离矩阵。当出现事故后，可以根据当前的运行状态，查找最接近的运行方式的电压灵敏度矩阵和电气距离矩阵作为控制方案的依据。利用计算出的孤立电网系统的电压灵敏度矩阵和电解铝负荷的电压调整量可以计算出发电机节点的电压调整量。需要说明的是，系统在不同拓扑结构下，其灵敏度参数会发生相应变化。对于文中的孤立电网，其拓扑结构的变化有限，因此可以在离线方式下对有限拓扑结构的灵敏度矩阵进行计算，然后再在实际运行中予以匹配。

根据广域测量系统WAMS检测到的不平衡功率可以计算出三期电解铝负荷分别需要降低的电压ΔULi(i＝1，2，3)，即三期电解铝负荷节点的电压变化量 ΔUL1，ΔUL2，ΔUL3为已知量，利用系统的电压灵敏度矩阵可以计算出发电机节点的电压变化量，如式 (11)所示，其中aij为节点i的电压变化量对节点j的电压变化量的灵敏度值。

通过式 (9)可以得知电解铝负荷具有较强的电压调节特性，具有负的频率调节特性，但是调节能力较弱，忽略不计。

假设电解铝负荷母线的初始电压为ULi，电解铝负荷母线需要降低的电压为ΔULi(i＝1，2，3)，电解铝负荷调整前的负荷大小为P0，电压为U0，调整后的负荷大小为P，电压为U，那么电解铝负荷节点需要调整的电压为:

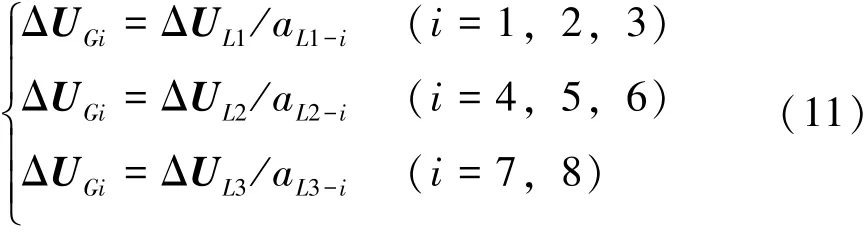
4 仿真研究

不考虑风电场接入孤立电网的运行方式下，风电场输出的有功功率为0，8台火电机组孤网运行，在此种运行方式下系统的总有功功率为1 800 MW，系统备用容量为135 MW。假设4.0 s发生一个发电机切机事故，切除额定功率为300 MW的6号火电机组，6号火电机组事故前有功出力为278 MW，事故后系统损失了278 MW有功功率，与此同时，系统的备用容量也损失了22 MW，此时孤立电网系统的不平衡功率为165 MW，系统备用不足，出现频率崩溃和电压崩溃事故，考虑事故后0.1 s加入基于灵敏度的控制方法，下面进行控制方法有效性的仿真验证:

1)利用电压灵敏度计算方法计算出此种运行工况下的系统的灵敏度矩阵，其中铝厂一期负荷母线电压对1号火电机组机端电压的电压灵敏度计算结果为1.137，对2号火电机组机端电压的电压灵敏度计算结果为1.137，对3号火电机组机端电压的电压灵敏度计算结果为1.089 7；铝厂二期负荷母线电压对4号火电机组机端电压的电压灵敏度计算结果为1.128，对5号火电机组机端电压的电压灵敏度计算结果为1.070 2，对6号火电机组机端电压的电压灵敏度计算结果为1.070 2；铝厂三期负荷母线电压对7号火电机组机端电压的电压灵敏度计算结果为1.063 9，对8号火电机组机端电压的电压灵敏度计算结果为1.063 9。

2)计算出当系统出现165 MW不平衡功率时，三期电解铝厂需要降低的有功负荷及三期电解铝厂的负荷母线电压调整值。根据3.1节和3.2节的计算方法，得到三期电解铝厂需要降低的有功负荷和电解铝负荷母线电压调整量，结果见表3。

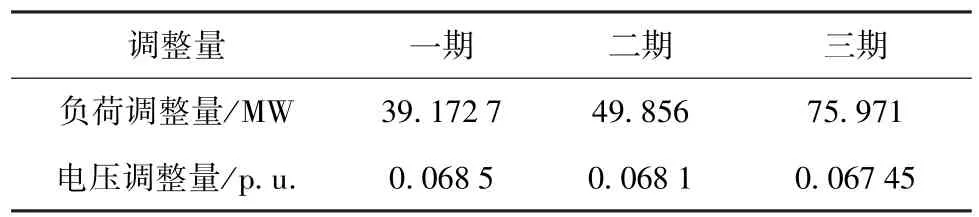
表3 铝厂负荷调整量和电压调整量

3)计算出发电机节点的电压调整量，根据3.3节的计算方法和步骤1计算出的灵敏度矩阵及步骤2计算出的电解铝负荷节点电压调整量，得到火电机组的机端电压调整量，结果见表4。

表4 火电机组的机端电压调整量

4)对比未采取控制和采取文中所提方法后孤立电网系统的响应，验证控制方法的有效性。图1和图2是未采取控制措施时系统的频率响应和电压响应曲线。采用控制方法后系统的频率响应和电压响应如图3和图4所示。

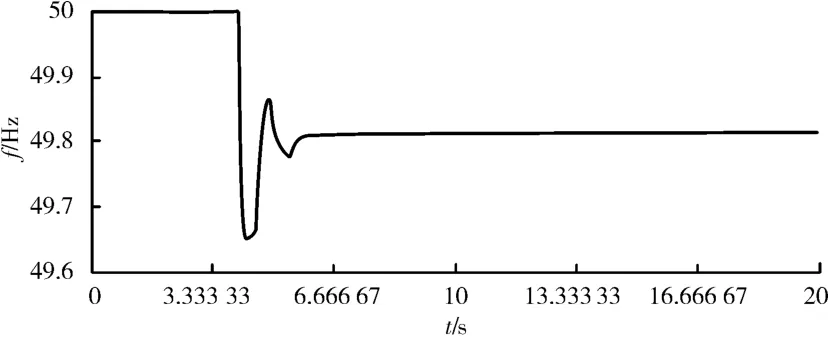
图3 系统的频率响应曲线

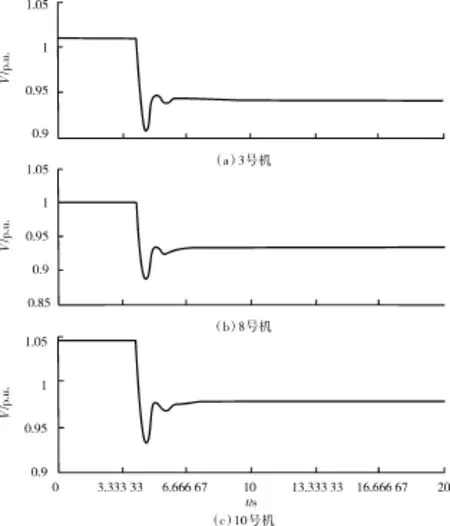
图4 系统的电压响应曲线

未采取控制措施时，4.0 s系统发生切除300 MW火电机组事故后，系统的备用不足，仅为135 MW，存在165 MW的不平衡功率，未采取任何控制措施时系统的频率和电压迅速崩溃。采取基于灵敏度分析的控制方法后，孤立电网系统的频率和电压都能恢复到正常的运行范围内，其中系统的频率降低到49.815 Hz，降低了0.185 Hz，三期电解铝负荷的电压标幺值分别降低了 0.068，0.07和0.065 4。

5 结论

采取基于电压灵敏度分析的控制方法可以有效的消除系统的不平衡功率，有利于维持系统的稳定运行，对于实际运行的孤立电网具有较普遍的适用价值。

〔1〕魏国华.基于灵敏度的网损分析和网络参数的综合优化 〔D〕.秦皇岛:燕山大学，2010.

〔2〕姜新凡，严庆伟，周帆，等.基于实时灵敏度分析的湖南电网无功电压优化控制系统 〔J〕.电网技术，2004，28(16): 82-85.

〔3〕Sun H B，Zhang B M.A systematic analytical method for quasisteady-state sensitivity〔J〕.Electric Power Systems Research，2002，63(2):141-147.

〔4〕吴政球，黄庆云，潘纪良，等.N－1网络电压及灵敏度快速算法 〔J〕.电力系统及其自动化学报，2009，21(1):118-123.

〔5〕谢会玲，鞠平，罗建裕，等.基于灵敏度计算的电力系统参数可辨识性分析 〔J〕.电力系统自动化，2009，33(7):17-21.

〔6〕陈曦.基于灵敏度方法的电网安全校正策略研究 〔D〕.保定:华北电力大学，2011.

〔7〕李大虎，曹一家.基于SCADA/PMU混合测量的广域动态实时状态估计方法 〔J〕.电网技术，2007，31(6):72-78.

〔8〕 Lagonotte P，Sabonnadiere J C，Leost J Y，et al.Structural analysis of the electrical system:application to secondary voltage control in France〔J〕.IEEE Transactions on，Power Systems.1989，4(2): 479-486.

〔9〕Stankovic A，Ilic M，Maratukulam D.Recent results in secondary voltage control of power systems〔J〕.IEEE Transactions on Power Systems，1991，6(1):94-101.

〔10〕Hauer J F，Mittelstadt W A，Martin K E，et al.Use of the WECC WAMS in wide-areaprobingtestsforvalidation ofsystem performance and modeling〔J〕.IEEE Transactions on Power Systems，2009，24(1):250-257.

〔11〕常乃超，兰洲，甘德强，等.广域测量系统在电力系统分析及控制中的应用综述 〔J〕.电网技术，2005，29(10): 46-52.

〔12〕Taylor C W.Power system voltage stability〔M〕.US:McGraw-Hill Companies，1994.

Frequency control method of isolated grids based on sensitivity analysis

WU Yunliang1，XIAO Zheng2，LIAO Siyang3
(1.China Southern Power Grid Power Operation and Control Center，Guangzhou 510000，China；2.Wuhan Electric Power Design Institute，Wuhan 430000，China；3.Wuhan University，Wuhan 430000，China)

Based on the actual isolated power grid with high energy consumption load in a certain area，the simulation studies are conducted in the real-time digital simulation platform.The security and stability control strategy is analyzed under different operation mode.The analysis results point out that power imbalance still exists in the isolated power system after the security and stability control device acts successfully under the extreme conditions.A control method to eliminate the power imbalance based on the voltage sensitivity analysis is proposed.The simulation results verify the effectiveness of the proposed control method.

voltage sensitivity；unbalanced power；isolated grids；frequency control

TM732

A

1008－0198(2016)06－0013－05

10.3969/j.issn.1008－0198.2016.06.004

吴云亮(1984)，男，湖北丹江口人，工学博士，研究方向为电力系统稳定与控制。

2016－09－26 改回日期:2016－10－13