基于推理公式的典型小流域防洪计算分析

2016-03-29崔积家桑国庆山东省水利勘测设计院山东济南5004济南大学山东济南500山东省工程咨询院山东济南500

山东水利 2016年2期

崔积家，桑国庆，袁　泉（.山东省水利勘测设计院，山东济南5004；.济南大学，山东济南500；.山东省工程咨询院，山东济南500）

基于推理公式的典型小流域防洪计算分析

崔积家1，桑国庆2，袁泉3
（1.山东省水利勘测设计院，山东济南250014；2.济南大学，山东济南250022；3.山东省工程咨询院，山东济南250013）

【摘要】本文将传统推理公式应用于山洪防灾对象的洪峰流量计算中，基于ArcHydro提取小流域参数，采用EXCEL编程迭代求解，计算典型流域5个防灾对象不同设计频率下的洪峰流量及汇流时间，提高了运算精度和效率，可为山洪灾害防治小流域洪峰批量计算提供参考。

【关键词】小流域；防洪减灾；推理公式

威海市文登区地处胶东半岛东南部，频临黄海，是暴雨多发地区，暴雨多由强对流、台风等造成，所形成的洪水具有陡涨、陡落特点。由短历时暴雨引发的山区地表径流，易造成河道水位猛涨，产生漫堤、水库溃坝、农田淹没等一系列山洪灾害，给区域内人民生命和财产造成重大损失。本文选取的典型流域包括亮夼、小界石、大界石村（界石镇驻地）、场东和板桥5个重点防灾对象。在小流域划分的基础上，基于1∶5万DEM进行各防灾对象以上汇流参数计算。

1　推理公式计算原理

推理公式是一种利用成因推理，并结合经验分析的暴雨洪水计算方法。推理公式法结构简单，参数较为简单，对资料条件要求不高，特别适用于无资料地区小流域的设计洪水计算。本文利用该方法进行山洪防灾对象的设计洪水计算。

1.1计算原理

按照《水利水电工程设计洪水计算规范》，参考中国水利水电科学研究院推理公式计算各子流域的洪峰流量和汇流时间。公式如下：

Qm，p为设计P频率下的洪峰流量，m3/s；F为流域面积，km2；τ为汇流历时；tc产流历时；L为沿主河道从出口断面至分水岭的最长距离；J为沿流程L的平均比降；μ为损失强度；n为暴雨衰减系数；m为汇流参数；θ为流域特性参数θ=L/J1/E· F1/4；其中F、L、J参数值，由ARC－hydro提取。Sp为雨力，即t=1h频率为P的平均雨强，mm/h，对于各频率下Sp由年24h最大降雨量计算：Sp= H24，p24n－1。

1.2计算流程

1）以产流模型计算成果作为输入，由各时段净雨统计得降雨过程t历时内的净雨总量。2）部分汇流时，τ＞tc，计算tc、τ、和Qm。假设汇流时间，由公式计算对应的洪峰流量。3）根据流量及汇流参数，由公式计算汇流时间。4）重复第2）、3）步，通过不断假设和试算，直到为止，此时对应的流量和汇流时间即为所求。5）根据以上计算的洪峰流量，按照该汇流分区对应的洪水概化过程线可得到对应的洪水过程数据。

1.3洪水过程线推求

文登区流域洪水过程线可以利用《山东省水文图集》中提出的概化过程线表推求，如图1所示。

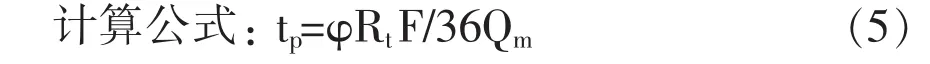
式中：Qm为计算的洪峰流量、tp为设计洪水流量过程的涨水历时，h；φ流域经验系数，小于和等于5km2为1.70，大于5km2、小于等于50km2为1.6，大于50km2为1.5；Rt为推求洪峰流量的平均净雨深mm。洪水总量用以下公式计算。

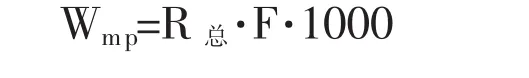
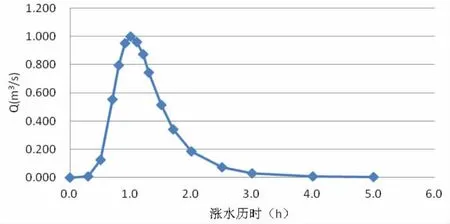
图1　洪水概化过程线

2　基于ArcHydro的小流域参数提取

以1∶5万DEM数据为基础，利用ArcHydro工具提取推理公式计算所需要的参数数据。本文利用Archydro工具，提取小流域流域面积F、最长汇流路径长度L、入口高程、出口高程、最长汇流路径比降等参数，为推理公式计算提供可靠数据。5个典型防灾对象提取的基础参数见表1。

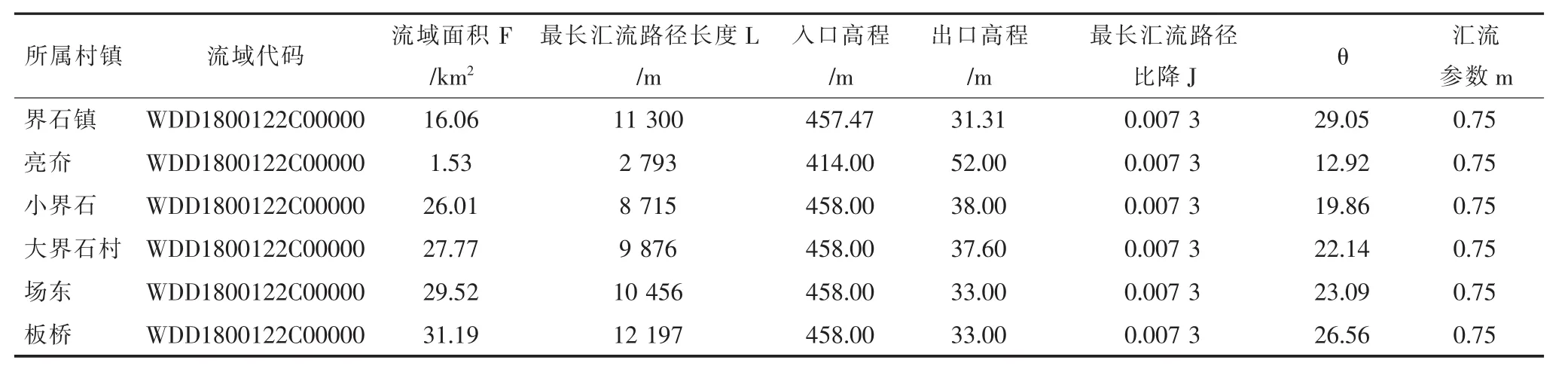
表1　小流域内各防灾对象汇流参数统计

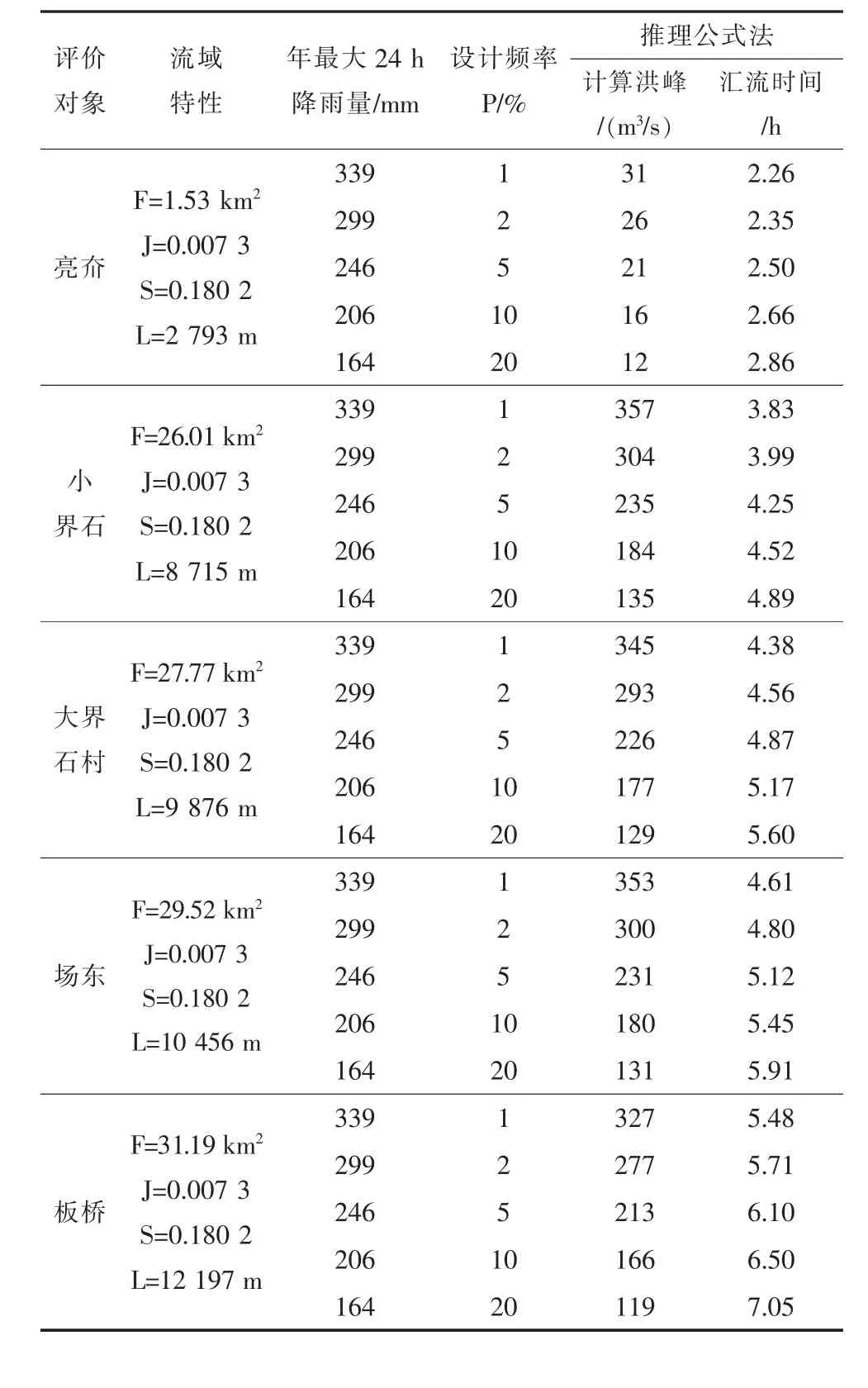
表2　流域5个防灾对象洪峰及汇流时间表

3　典型小流域计算实例

根据提取的各防灾对象汇流参数数据，可进行推理公式运算，求解洪峰流量和汇流时间。推理公式求解可采用图解法、简单迭代法和牛顿迭代法分析法。本文中采用EXCEL中单变量求解工具进行迭代求解，简化了计算过程，典型流域5个防灾对象不同设计频率下（5年、10年、20年、50年、100年）的洪峰及汇流时间成果见表2。