不规则结构的扭转指标调整初探

胡冰（中石化上海工程有限公司，上海 200120）



不规则结构的扭转指标调整初探

胡冰
（中石化上海工程有限公司，上海 200120）

摘 要通过对高层框架结构扭转的研究，结合工程实例总结对SATWE结果分析过程中有关结构平动周期、扭转周期、周期比的有效调整方法，对今后设计过程中遇到类似问题可以作为参考。

关键词不规则结构；平动周期；扭转周期；周期比

目前国内结构设计运用最广泛的结构分析软件是PKPM，作为结构工程师应该熟悉并了解其特点，在设计时应善于运用理论知识对其进行各项参数的调整。

一般情况下，采用结构布置规则、对称、刚度均匀的结构体系，能够减少扭转效应，然而由于某些因素，建筑结构并不能够做到完全规则，会增加对结构扭转指标调整的难度。国标《建筑抗震设计规范》（GB 50011—2010）和《高层建筑混凝土结构技术规程》（JGJ 3—2010）中，给出了有关结构抵抗扭转的量化指标，当设计结构时需要调整模型参数，使之符合规范要求。本文基于规范，通过工程实例，对SATWE后处理分析环节中有关结构的平动周期、扭转周期、周期比超限的调整提出一些建议。

1 工程概述

某医药项目办公楼，层高24.2 m，呈L型布置。长30 m，宽18 m，总共7层，属于A级高度的高层建筑。根据《高层建筑混凝土结构技术规程》3.4.3（3）中，l /Bmax< 0.35，符合规范[1]对结构不规则的限定。框架抗震等级为二级，地震加速度为0.10 g，设计地震分组为第三组，抗震设防烈度为7度。初定框架柱尺寸500×500，框架梁尺寸350×500，参见图 1。

根据上游专业条件要求，在D~F轴有几个楼层将设置资料室、阅览室，因此需将此区域（以下简称A区域）的活荷载设为5 kN/m2，其他区域活荷载按规范[2]活荷载取值2 kN/ m2（本算例为表达简明将楼梯、电梯井等结构去除）。

图1 办公楼平面Fig. 1 Office building plan

在建模时采用刚性楼板假定。将模型输入后，在周期、地震力与振型输出文件WZQ.OUT文件中，查得数据见表1。

表1 初始结构振型周期Tab.1 Original free vibration mode

根据平动系数可以看出，第一振型和第二振型平动系数均大于0.5，属于平动周期，而第三振型的扭转系数为0.94 > 0.50，且周期相对于后续振型较长，判定其为第一扭转周期。因此前三振型号可以代表本结构的基本振型周期，后文将仅罗列前三振型。

《高层建筑混凝土结构技术规程》规定，结构平面布置应考虑减小结构扭转程度。周期比，即结构扭转为主的第一自振周期Tt与平动为主的第一自振周期T1之比，A级高度高层建筑不应大于0.9，B级高度高层建筑不应大于0.85。

将第一扭转周期（振型号3）除以第一平动周期（振型号1），得到Tt/ T1= 1.305 1/1.442 6 = 0.904 6，大于A级高层的标准0.9，不满足规范要求。可以判断是由于结构平面的不规则，导致结构周期比不符合规范要求。

在周期比不满足规范要求的情况下，可以在SATWE图形结果中查看结构整体空间振动图，通过观察三维的振型动画可以了解整体结构的振动形态，判断其是否在某处有薄弱处以及不合理的布置。通过查看第一、第二、第三振型的整体振型图，可以看到除第一振型在平动的过程中稍微掺杂了一些扭转，但不是很明显，正好对应了第一振型的扭转系数偏大的情况。第二个振型主要为平动振型，第三振型为扭转振型。初判断其是由于平面荷载不规则引起的，楼层大部分区域均为2 kN/ m2，唯独在A区域有几层活动荷载为5 kN / m2，显得有些失衡。

1.1 问题简述

通过以前设计经验判断，如果能够将这部分荷载改小或者移动至结构中心，则荷载在平面中将更加均匀，对结构有利，使层间位移比与周期比都可以降低。由于在设计的初期，通过与上游专业讨论后，得知其原本预留资料室的活荷载其实并不需要规范上规定的那么大，仅有少量书架供阅览使用。因此按照荷载规范将荷载改小至2.5 kN/m2。

在模型中重新修改活荷载后，经过计算分析，重新查看振型输出文件WZQ.OUT，查得前三组数据如表2。

表2 调整后结构前三振型周期Tab. 2 Adjusted free vibration mode

分析结果与之前预想的不同，第一振型的周期减小而第三振型的周期增大，导致周期比Tt/ T1= 1.311 6 / 1.4289 = 0.917，反而增大了。经过校对输入荷载以及模型设置的选项后均没有发现错误。因此需要查找其增大的原因并进行分析，从中找到对结构周期比影响的关键因素，才能对调整有直接的帮助。

2 计算结果的分析

2.1 扭转的原因及其危害

分析扭转的原因首先需要了解扭转的概念。根据力学理论，外力偶矩导致构件中任意两个与该力偶矩平行的横截面之间存在一定的扭角，即为扭转。外力偶矩越大则扭角越大，超过构件承载极限发生扭转破坏，表现为受弯或受剪破坏。

在图2中可以看到，侧向振型（平动）时结构平面中所有质点的位移都基本相同的，朝x方向或者y方向分别振动。见图2中的振型1和振型2。而扭转振型则是整个结构绕着一个点进行扭转，离结构中心越远的构件，其移动的幅度越大，这是扭转运动的特点。因此扭转振动带给结构的危害要远远大于侧向振动，特别是结构的周边部分，相对于结构中心的位移要大很多，见图2中的振型3。

图2 结构整体空间振动（振型1，振型2，振型3）Fig. 2 Free vibration modes （mode1 ，mode 2 ，mode 3）

根据SATWE软件对扭转系数的描述，扭转系数是结构抗震设计的一个控制参数。当一个结构自由振动时，一个振型的反应能量可以拆分为侧振能量与扭振能量，扭转系数定义为扭振能量和总反应能量的比值。

对于需要控制扭转效应的结构，都是通过控制周期比来限定的，查看以结构扭转为主的第一周期（即第3振型）与以平动为主的第一周期（即第1振型）之比，就是之前叙述在规范中要求限定的比值。要判断第一平动周期就是看扭转系数最小的振型周期，判断第一扭转周期即是扭转系数最大的振型周期。平动系数与扭转系数之和为1。

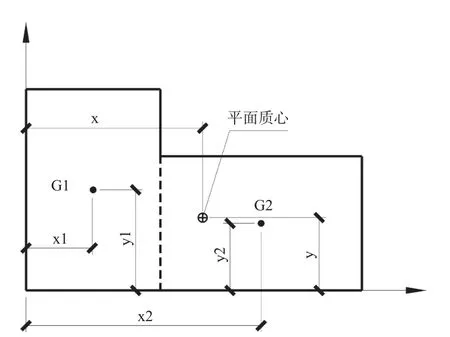
图3 质量中心Fig. 3 Example of the gravity center

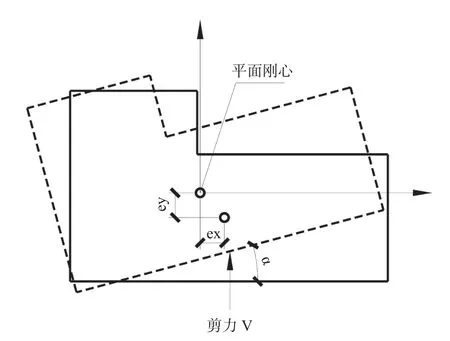
图4 刚度中心Fig. 4 Example of the rigidity center

扭转产生的原因是结构平面的质量中心与刚度中心不重合，对于地震荷载而言，质量中心是指等效地震作用合力点，即惯性力的合力作用点，它与质量分布有关，结构质量越大惯性力也越大。以下简称质心，参见图3。

刚度中心是指所有结构抗侧移刚度的中心，抗侧移刚度是指抗侧力结构单元在单位层间位移下所需要的剪力值。刚度中心简称刚心，参见图4。

通过查看振型号3的第三自振周期图，可以看到框架的各竖向构件的水平方向位移不是沿x方向或y方向完全相等，而是以刚度中心为中心，各个构件距离该中心越远，其水平方向位移越大，同时附加扭转作用也越大。

当质心与刚心不重合时，惯性力作用于质心，与质心刚心距离乘积形成扭矩，造成结构同层位移分布不均。结构质心和刚心的不重合往往是由于结构的不对称或不规则引起的，引起不规则结构的偶然偏心因素很多，比如荷载分布的不均匀，构件强度分布不均匀。

2.2 扭转指标的理论推导

通过对平面的刚性假定，可以推算出结构平面绕刚心的扭转刚度。

假设构件i在x方向和y方向的抗侧移刚度分别为kxi、kyi，并假定楼板是完全刚性的，结构的全部质量m都集中在楼板上，则该结构的质心坐标xm、ym分别为：

ρ 为楼板的面密度，为坐标x和y的函数，A是楼板面积。

楼板绕质心的转动惯量Iθ为

结构的刚心坐标xk、yk分别为：

xi、yi分别为框架柱截面中心点坐标。

结构绕刚心的扭转刚度kt为：

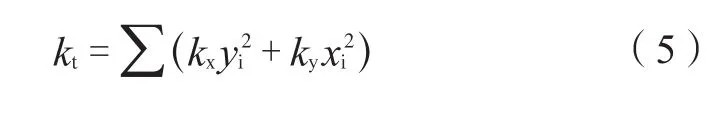
其中kx、ky分别为结构x，y方向总抗侧移刚度。

为了了解结构周期比与结构质心、刚心偏离量的关系，以及侧向刚度对结构自振周期的关系，可以通过建立运动学方程[3]推导周期比，可以通过以下公式表示为：

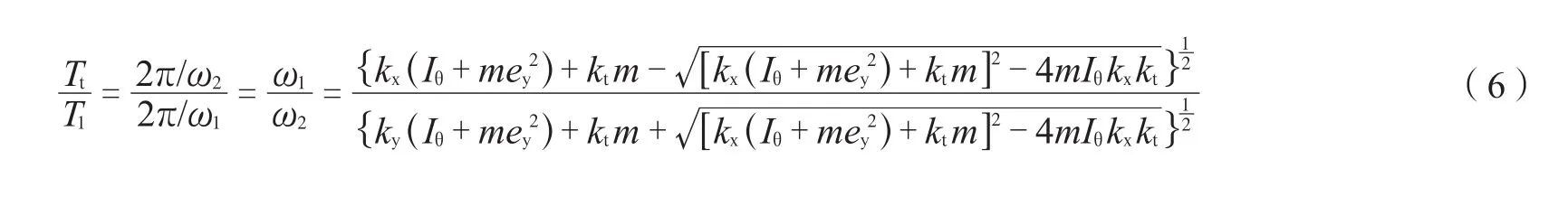
式中 ω—结构自振圆频率 ；

ey—表示结构质量偏心率。从式（6）可以得到，在某些情况下，当增大ey，即增大结构质心与刚心偏离量，能够减小周期比。同理，增大抗侧移刚度也可以减小周期比。也就是说质心、刚心偏离量以及结构的抗侧移刚度与周期比成反比，为了可以控制结构的扭转效应，可以调整这两个参数大小，使结构周期比符合规范的要求。

2.3 周期比增大的原因分析

通过以上的公式就可以说明在本工程实例中将结构A区域的活荷载减小，结构的周期比反而会增大的原因。将A处的活荷载减小，使得结构平面中的荷载更加均匀，令质心与刚心的偏离量缩小了，结构的扭转周期与平动周期的比值（周期比）就变大了。因此可以反向思维，利用增加质心与刚心的偏移量进行减小周期比，但这种方法应注意可能会引起结构的扭转位移偏大，因此不推荐此方法。

我们可以看出，当结构质心与刚心的偏离量以及结构抗侧移刚度之间正好存在某种关系，调整荷载使其更加均匀反而造成周期比的增大。但是在结构设计中，还是要遵从采用结构布置规则、对称，平面布置刚度均匀，以减少扭转的程度，不能只看周期比这一个参数，更应注重结构整体的抗扭转刚度与抗侧移刚度的关系。

周期比Tt/ Tl与结构的抗扭刚度kt、抗侧刚度kl、转动惯量mt以及质量ml有如下关系[4]：

从式（7）可以判断，提高构件的抗扭转刚度就可以降低扭转效应，为了更有效提高结构的扭转刚度，结构设计应对称均匀，面积跨度均不能太大，从而可以控制平面的转动惯量与质量的比值。当由于建筑需要不能避免不规则平面的情况下，应将结构具有较高抗扭转刚度的构件在结构布置在适当位置。同时结构抗扭转刚度不能太弱，关键还是要控制抗扭转刚度与抗侧移刚度的关系。

当Tt和Tl接近时，由于振动耦联的影响，结构的扭转效应将会明显增大。所以在抗震设计中应采取各种措施减小其比值，使结构具有必要的抗扭转刚度。

结构自振周期表示结构自身的性能，其中扭转周期的相对大小能够反映结构抗扭转刚度的大小。抗扭转刚度较大的结构，其扭转周期必然也较小。通过式（5）可以推导出结构的抗扭转刚度kt与x 向抗侧移刚度klx、Y向抗侧移刚度kly及构件抗扭转刚度kti有如下关系式：

由公式（8）、（9）、（10）可以看出，抗震设计时应注意结构的合理布置，提高抗扭转刚度kt与抗侧移刚度kl的比值，就可减少Tt/ Tl，从而减轻扭转效应对结构的影响。其次根据公式中抗扭转刚度与抗侧移刚度之间的关系，增加结构的抗侧移刚度，尤其是距离中心更远的构件抗侧移刚度，对结构的抗扭更有利。

以上推断可以看出，要控制结构的周期比，需要尽可能合理均匀布置结构平面，避免结构平面的不规则；提高抗扭转刚度也可以控制周期比，在抗侧移刚度的作用下，周期比会根据它们之间的大小有所变化。

综上所述，要控制周期比，可以根据影响结构周期比的因素，得出以下对周期比的调整方法，参见图5。

图5 调整周期比的方法Fig. 5 The process of cycle ratio adjustment

3 工程实例试算与比较

为了验证之前的推导是否正确有效，就需要用工程实例来进行试算，观察其结果与之前总结的是否一致。

首先在模型参数不变的情况下，调整其结构构件的尺寸。将所有柱的尺寸从500×500调整为550×550。查得前三组数据见表3。

表3 增加全部柱截面后振型周期Tab. 3 Free vibration modes after all columns enlarged

从上述计算结果可以看出，将框架柱截面尺寸增大后，结构的自振周期有所降低，周期比Tt/ T1= 1.179 6 / 1.313 4 = 0.898达到规范要求，第一振型中的扭转系数也明显减小了。可见加大柱的截面尺寸可以明显的提高结构的抗侧移刚度，从而减小周期比。

根据公式（8）、（9）、（10）得出的结论，尝试一下只增加外侧柱，即A、F、1、3、4轴上的柱，增加其尺寸到550×550，内部的柱还是维持原状的500×500，这样既可以减少混凝土的用量，而且根据上述推导，能够更加提高抗扭转刚度从而减轻扭振效应。计算结果见表4。

表4 增加外侧柱截面后振型周期Tab. 4 Free vibration modes after outside columns enlarged

调整结果很明显，周期比Tt/ T1= 1.097 9 / 1.272 3 = 0.863，相对于增加全部柱尺寸方法的周期比更小了。这是因为增大外圈的框架柱能够增大扭转刚度，减小结构的抗扭周期，而抗侧移刚度并没有较大提高，作为分母的抗侧移周期没有明显变小，从而达到减少结构周期比的目的，结果与之前的推导保持一致。

用相同方法，增加外侧框架梁的尺寸来增加抗侧移刚度和抗扭转刚度，柱截面改回至原来500×500，框架梁截面有原来350×500增加到350×600。分析后结果见表5。

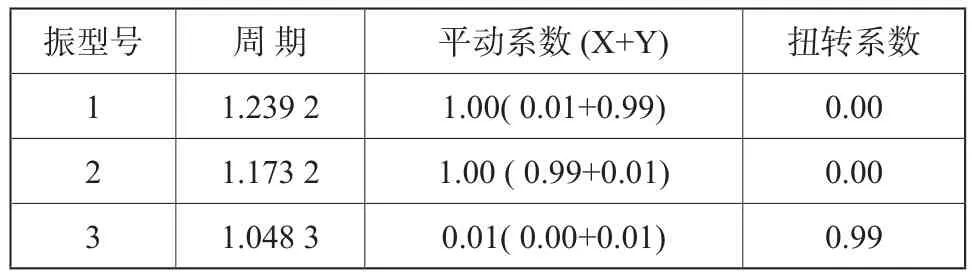
表5 增加外侧梁截面后振型周期Tab. 5 Free vibration modes after outside beams enlarged

结构的周期比Tt/ T1= 1.048 3 / 1.239 2 = 0.845，比调整柱的尺寸更小了，说明结构整体扭转刚度相对于抗侧移刚度增大了。通过观察结构振动模型，第一振型与第二振型均为平动振型，模型扭转指标基本调整到位。将整个结构看做一根柱，增加梁的截面尺寸相当于提高该柱的抗扭箍筋，对其扭转位移进行约束。由此可见，通过增加外侧框架梁的截面高度，比加大框架柱尺寸对结构的整体抗扭转刚度更有效。

经过了以上几种不同方法进行试算，分别比较其计算结果，最后决定采用加大外侧框架梁高的方案。此方案不仅减轻扭振效应，又可以控制抗侧移刚度和抗扭转刚度之间的平衡，达到较好控制周期比的效果。调整结果比较参见图6。

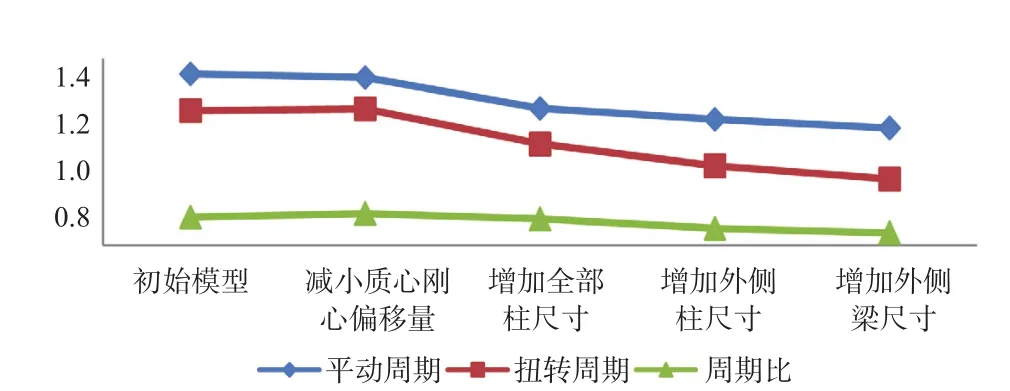
图6 不同调整方法的周期比结果比较Fig. 6 Results compare of different adjustment methods

从图6可以看出，增加外侧梁尺寸的方法对结构抗扭转能力提高最为明显，能够较大幅度提高抗扭刚度，控制抗侧移刚度，减小周期比。其次增加外侧柱尺寸的方法也很有效，因此可根据实际情况进行调整方法的选择。不同调整方法的有效性比较可参见表6。

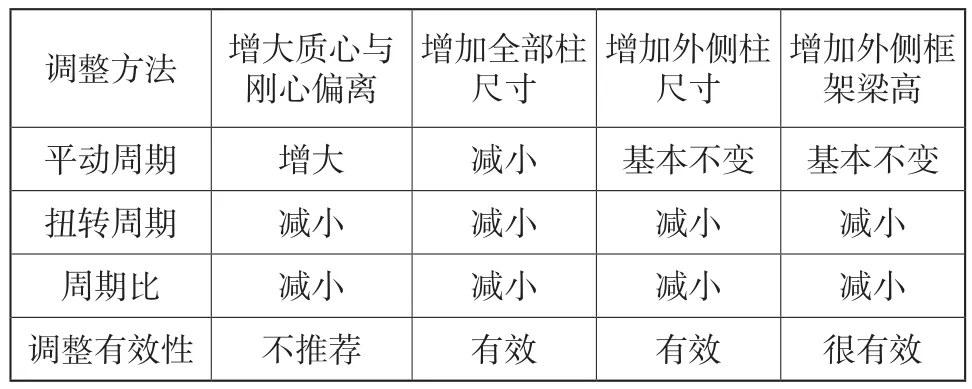
表6 不同调整方法的有效性比较Tab. 6 Effect compare of different adjustment methods

4 结束语

针对该工程实例与理论分析，通过对结构的平动周期、扭转周期、周期比的影响因素进行总结，结果表明：

（1）结构产生扭转是结构质心与刚心不重合引起的，为避免构件因扭转而产生破坏，应对其周期比进行限制。周期比与结构质心和刚心的偏离量、结构平面的转动惯量、结构的抗侧移刚度、抗扭转刚度有关。在地震作用时，平动振型和扭转振型同时产生，互相作用与牵制，因此周期比会由于结构抗侧移刚度及抗扭转刚度之间的关系而变化。

（2）一般来说，提高外侧框架梁高能够更有效的提高结构整体的抗侧移刚度，也能加强结构的抗扭转能力，应该在调整周期比的过程中首先采用，再考虑增加外侧柱尺寸，以及其他可以增加抗侧移刚度的构件。当结构扭转程度较大时，仅增加外侧的构件刚度，内部构件不做调整，能够显著增加结构的抗扭转刚度，而抗侧移刚度增加并不明显，这样做的目的在于减小结构的扭转周期，同时不会明显减小结构平动周期，从而使周期比变小。

（3）调整结构周期比只是调整结构参数的一方面，还应注意结构整体的抗扭转刚度与抗侧移刚度的关系，不能盲目为调整周期比而忽略结构整体的合理性。

参考文献

[1]JGJ 3—2010. 高层建筑混凝土结构技术规程[S].

[2]GB 50009—2001（2006年版）. 建筑结构荷载规范[S].

[3]吕西林，周德源，李思明，等．建筑结构抗震设计理论与实例[M]．上海：同济大学出版社，2002.

[4]徐培福，黄吉锋，韦承基 高层建筑结构在地震作用下的扭转振动效应[J]. 建筑科学，2000（1）.

欢迎订阅《化工与医药工程》

（邮发代号4—910）

《化工与医药工程》创刊于1980年，是经国家科技部、国家新闻出版广播电影电视总局正式批准，面向国内外公开发行的专业技术期刊。由中国石油化工集团公司主管，中石化上海工程有限公司主办。

《化工与医药工程》为双月刊，大16开本，国内外公开发行。欢迎有关单位和个人订阅。

订阅价格：人民币90元/年（含邮费）

订阅方式：通过邮局订阅，邮发代号4—910

或通过邮局、银行汇款，并将订阅信息发送至本刊发行部

邮箱: 1027288568@qq.com 电话：（021） 32140428转122、108

Discussion of Regulation for Torsion Index of Irregular Structure

Hu Bing
（SINOPEC Shanghai Engineering Co., Ltd, Shanghai 200120）

Abstract:With the study of torsion occurred in high frame structure and the engineering experiences, the effective methods for regulating the horizontal vibration cycle, torsion cycle and cycle ratio of structure were summarized, which may be used for reference in later design.

Keywords:irregular structure; horizontal vibration cycle; torsion cycle; cycle ratio

通讯地址：上海市延安西路376弄22号（永兴商务大楼）11楼 邮编：200040

作者简介：胡冰（1982—），男，工程师，主要从事石油化工、医药工程结构设计。

收稿日期：2015-08-26

中图分类号：TU 318+.6

文献标识码：A

文章编号：2095-817X（2016）01-0012-000