基于梯度计算的自动聚焦图像清晰度评价函数仿真分析

潘雪娟，朱尤攀，潘 超，韩 娟，李大庆，张 皓，罗 琳，李泽民



基于梯度计算的自动聚焦图像清晰度评价函数仿真分析

潘雪娟1,2，朱尤攀1,2，潘 超1，韩 娟1，李大庆3，张 皓1，罗 琳1，李泽民1

（1. 昆明物理研究所，云南 昆明 650223；2. 微光夜视技术重点实验室，陕西 西安 710065；3. 中国人民解放军63963部队，北京 100072）

基于梯度计算的评价函数在自动聚焦系统中应用广泛，函数形式变化多样，本文基于图像梯度计算的数学原理，通过MATLAB仿真分析，对比了常见梯度类评价函数的性能，总结了梯度类评价函数应用中结合系统成像质量控制算法性能的方法。

梯度算子；评价函数；数学原理；自动聚焦；MATLAB

0 引言

在基于图像处理的自动聚焦方法中，准确的像质评价是聚焦位置搜索（占整个自动聚焦过程的大部分时间[1]）的前提，图像清晰度评价函数在闭环系统中非常重要。由于场景的随机性、成像系统的成像质量、噪声干扰等问题，目前并没有一种通用的评价函数能够适用于所有场合。在众多评价函数中，基于像素梯度计算的评价函数数量大、变化多、应用广，各种梯度类评价函数的差别主要体现在梯度算子的不同，即差分对像素灰度变化不同的近似（方向、阶数），以及像素梯度到评价值的映射处理，即对高频信息的衡量（取绝对值、平方运算、求模等）。本文从梯度算子的数学原理出发，结合MATLAB仿真分析，对常见的梯度类评价函数比较，总结出一些基本的设计原则，对设计梯度类函数作为自动聚焦系统评价函数性能的把控提供参考。

1 基于梯度的评价函数原理

1.1 微分运算的差分近似原理

图像清晰度评价的原理：清晰图像比模糊图像对比度高，边缘细节丰富（高频分量多），评价函数的实质基本都在检测加强高频信息，梯度类函数以像素梯度反映灰度的变化情况。灰度局部变化用微分来检测，由于变化短促，一阶和二阶微分特别适合于这种目的[2]。如二维图像的二阶导数差分近似：拉普拉斯算子（梯度的散度）：

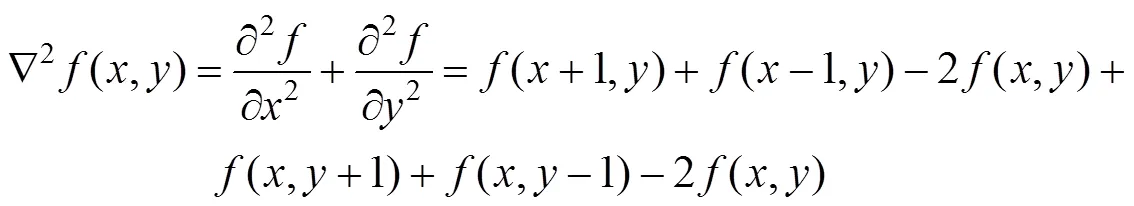
图像像素位置关系如下：

一阶导数通常在图像中产生较粗的边缘；导数的幅度可用于检测图像中的某个点处是否存在一个边缘。二阶导数对精细细节，如细线、孤立点和噪声有较强的响应，导数对每条边缘生成两个值，零交叉点可用于定位粗边缘的中心。在纯粹的二阶导数操作中就会出现对噪声的敏感现象，三阶以上的导数信息往往失去了应用价值。各种梯度算子的存在就是对这种导数分割原理进行实例化计算。图像微分的差分近似可以通过卷积滤波实现，式(1)的卷积核为：

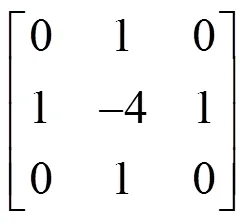
正是拉普拉斯4邻域梯度算子。观察差分运算式与其滤波模板的对应，梯度算子的差异主要在于：梯度方向、梯度计算间隔（微分运算阶数）。大的算子可以用于检测模糊边缘，小的算子可用于检测锐度集中的精细细节。实际中，数字图像都存在被模糊且带有噪声的边缘，模糊的程度主要取决于聚焦机理（如光学成像中的镜头），而噪声水平主要取决于成像系统的电子元件。梯度算子的选取和设计正是基于梯度计算边缘检测的一大类图像清晰度评价函数的重点，图像数据的随机性、噪声影响，如何保证边缘检测准确高效是需要考虑的问题。

1.2 梯度算子性能比较分析

1.2.1 单个梯度算子中包含的信息

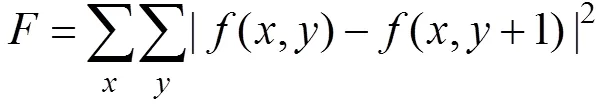
②阶数，梯度计算的间隔体现微分的阶数[2]，通常使用一阶或二阶的梯度算子。如梯度平方函数梯度算子对应一阶微分，Brenner函数对应二阶微分。对于二阶微分的近似，Sobel算子进行加权平均处理。从另一个角度考虑，图像对比度低的系统，如红外成像系统，图像边缘较粗，使用间隔一个像素计算梯度的函数评价效果可能更好。文献[3]中提到通过梯度间隔减弱噪声干扰，文献[4-5]对梯度间隔信息反映的频率特性进行了分析，文献[6]也讨论了梯度间隔信息。

1.2.2 多个梯度算子

对二维图像数据，综合两个互相垂直的方向梯度信息是合理的，常见单个梯度算子中只有拉普拉斯（4邻域）算子包含两个方向梯度信息，对图像的梯度算子模板根据差分近似必需满足的条件设计系数，在单个算子中包含两个方向不好设计，最简单的方法是同时使用计算两个梯度方向的算子，可对单个方向梯度算子进行处理提高准确性，如SML（Sum Modified Laplacian）函数的两个分别检测水平垂直方向梯度信息的算子对应拉普拉斯4邻域算子的两个方向，又如Sobel算子梯度计算间隔1个像素，并进行了加权平均处理。

2 像素梯度到评价值的映射算法

2.1 单个梯度算子

对单个梯度算子与图像矩阵卷积得到的梯度矩阵（每个像素点对应一个梯度值），将二维矩阵数据映射为一个评价数值，常见的有两种处理方法，取绝对值累加和平方累加，即梯度幅度均值越大，图像越清晰，平方运算加强梯度信息，但可能增强远焦区的波动，对阈值处理具有依赖性。

2.2 多个梯度算子

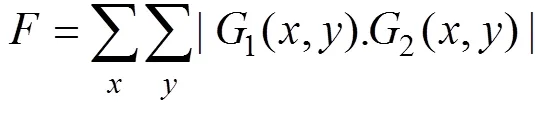
3 实验数据与分析

仿真平台：CPU：Intel(R)b Core(TM) i5-4590 @3.3GHz，3.46GB内存，计算环境：MATLABR2012b。

采用13组图像数据，其中，3组非制冷红外红外像，对比度低；6组制冷红外图像，对比度较非制冷红外图像高；4组可见光图像，对比度较高。图像序列依次对应离焦-聚焦-离焦的过程。文中采用图1所示的3组典型图像数据进行分析，第一组可见光图像对比度高，45幅图像中第30幅最清晰；第二组制冷红外图像，主体水平边缘丰富，背景云在动，81幅图像中第41幅最清晰；第3组非制冷红外图像，对比度低，22幅图像，前面的人在第9幅图最清晰，后面的人在第17、18幅图像清晰。

图1 典型图像数据

3.1 单个梯度算子方向与微分阶数对评价函数性能的影响

本节使用以下典型微分算子对图1所示的图像进行梯度计算，对比分析单个梯度算子的方向、阶数对图像边缘信息提取的性能，实验中整幅图像的信息综合都采用取绝对值累加的方法，结果见图2～图4。

一阶水平、垂直、－45°、＋45°方向梯度算子（后两个即Roberts算子）：

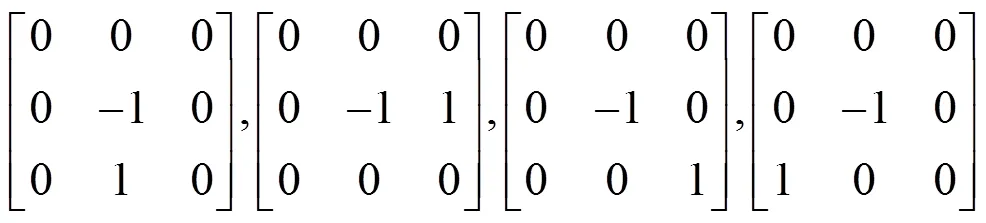
二阶水平、垂直、－45°、＋45°方向梯度算子：

二阶水平、垂直、－45°、＋45°方向梯度算子（间隔一个像素）：

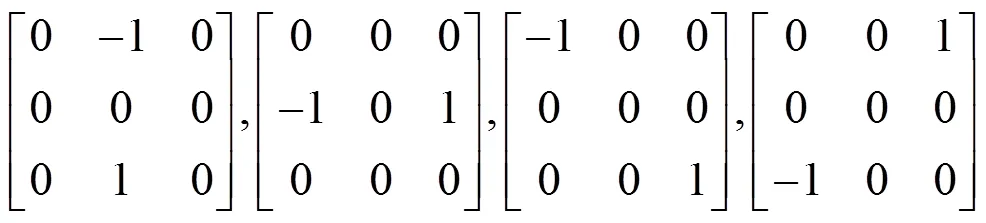
拉普拉斯4邻域、8邻域算子、对角方向梯度算子（二阶微分算子）：

由图2可以看出，对于对比度高的可见光图像，不同方向、阶数的梯度算子都准确聚焦，波动趋势基本相同。二阶垂直梯度算子效果最好，二阶算子比一阶算子和相隔一个像素计算的二阶梯度算子灵敏度好。

由图3可以看出，对图1所示的制冷红外图像，聚焦点两侧二阶水平梯度算子灵敏度最好，其次是一阶水平梯度算子。垂直方向的梯度算子全部对焦失败，联系图像序列的特点，主体水平边缘丰富，背景云在动，评价函数曲线波动也大。

由图4可以看出，对实验中采用的效果最差的非制冷红外图像间隔一个像素计算的二阶梯度算子性能最好，其次是一阶梯度算子，相邻像素计算的二阶梯度算子性能最差。

综上，梯度算子的方向和阶数对不同图像的评价并没有一致性，与实际边缘方向一致的算子具有更好的性能。总体来讲，对比度高的图像，相邻像素计算梯度的二阶微分算子比一阶微分算子灵敏度高，一阶微分算子比相隔一个像素计算梯度的二阶微分算子灵敏度高；对比度低的图像，梯度算子的灵敏度呈现与上述完全相反的顺序，实验中用到的非制冷红外图像边缘模糊，相隔一个像素计算梯度对边缘的检测更灵敏。梯度算子的方向和计算间隔应该根据具体的系统合理设计。

3.2 单个梯度算子的信息综合

3.1节中整幅图像的信息综合（像素梯度到评价值的映射算法）都采用取绝对值累加的方法，本节采用与3.1节相同的梯度算子，对应2.1节，采用像素梯度平方和累加的方法，对比不同梯度信息综合算法的性能，结果见图5～图6，结合图2～图4进行分析。

对比图2～图4可以看出，梯度绝对值累加的计算方法，图2显示对对比度高的图像波动较小，图3对比度降低，波动增大，图4对比度最低的非制冷红外图像，函数曲线波动严重。

由图5可以看出，梯度平方累加的计算方法，间隔一个像素计算二阶梯度算子和一阶梯度算子，梯度平方函数较绝对值函数性能大大提高，很好地抑制了离焦区的曲线波动。对单个算子的信息综合，为了抑制非边缘像素梯度参与计算产生的影响，可以进一步考虑阈值处理[7,12-14]、像数据归一化、赋权[15-16]等方法。

由图6可以看出，梯度绝对值函数对椒盐噪声的抗干扰性比高斯噪声强，梯度平方函数对高斯噪声的抗干扰性比椒盐噪声强，梯度绝对值函数对两种噪声的综合抗干扰性能比梯度平方函数强。

3.3 多个梯度算子信息综合

本节采用以下微分算子，结合二阶水平、垂直方向梯度算子及二阶水平、垂直方向梯度算子（间隔一个像素）计算图像梯度，对应2.2节梯度到评价值的映射算法，综合比较多个梯度算子的方向、梯度信息及信息综合方法对评价函数性能的影响，结果见图7～图10。

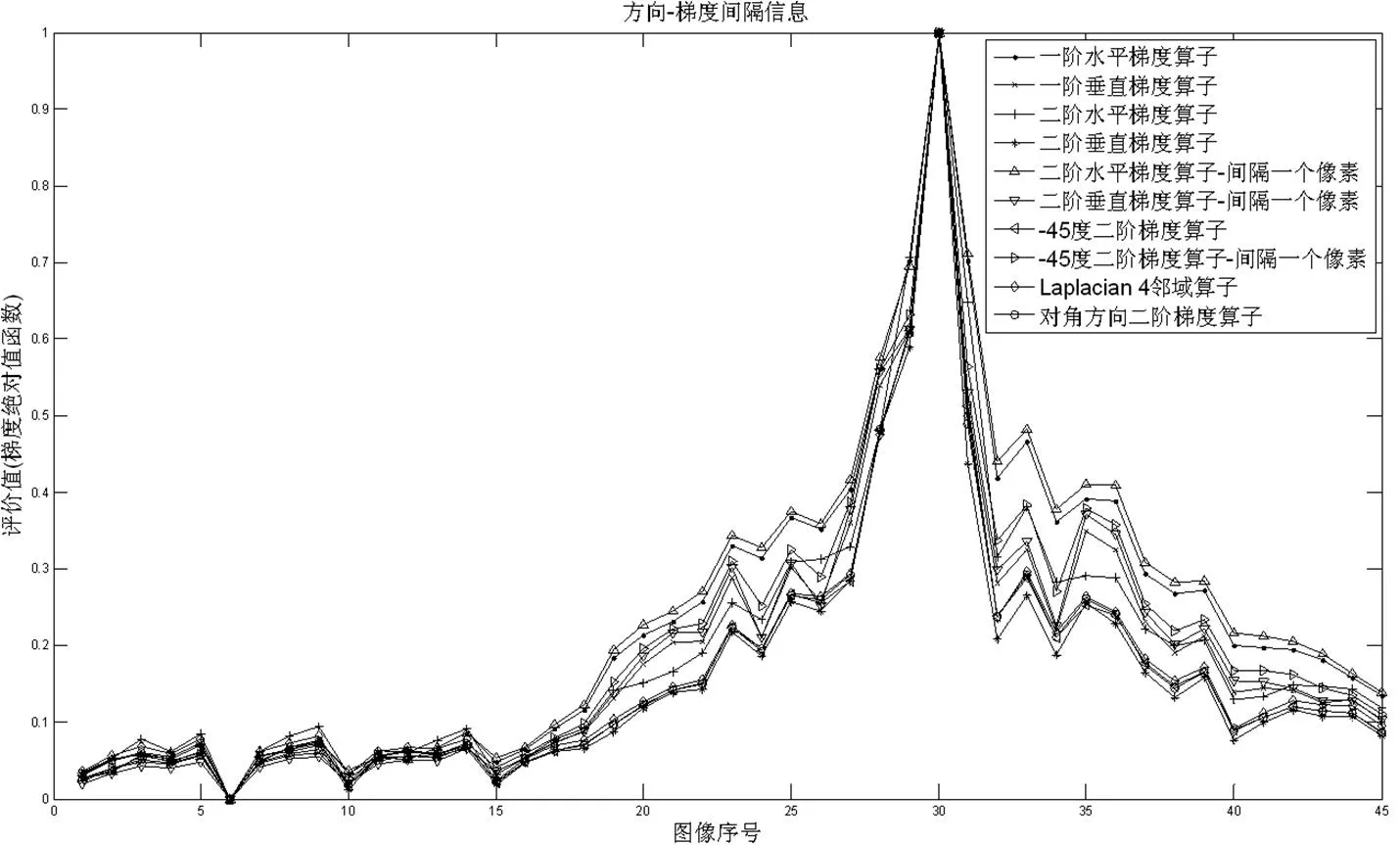
图2 不同梯度算子函数对可见光图像的评价效果

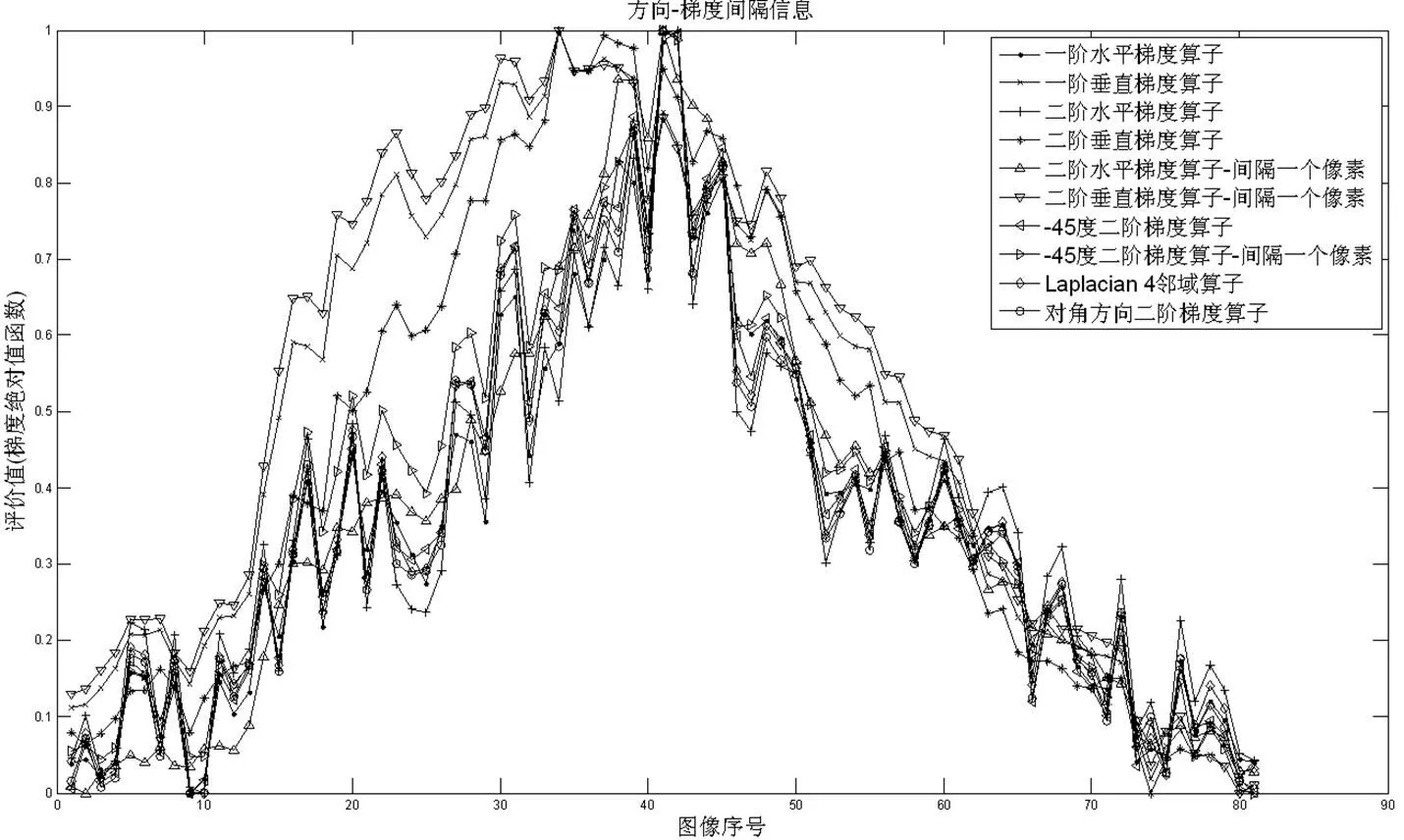
图3 不同梯度算子函数对制冷红外图像的评价效果

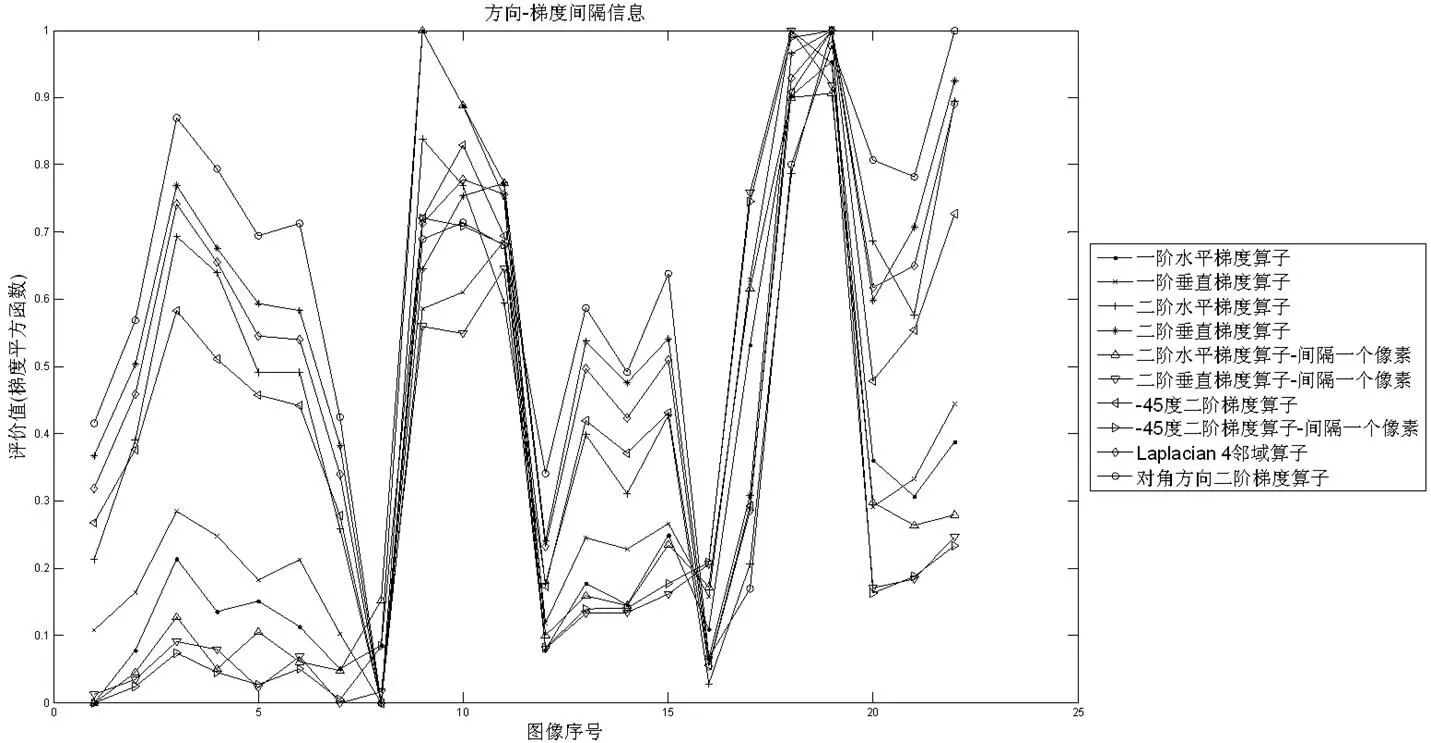
图5 非制冷红外图像梯度信息平方累加评价效果

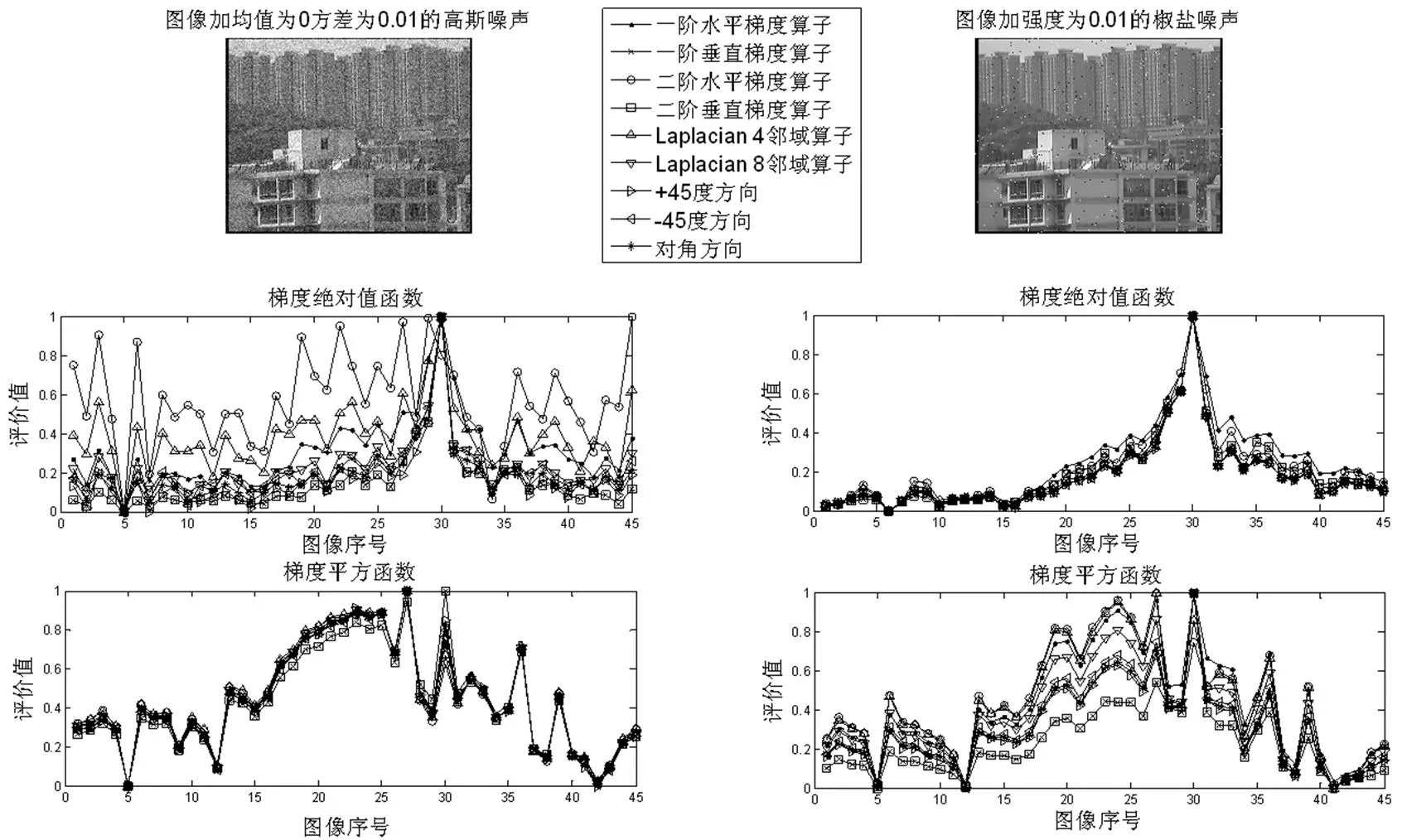
图6 抗噪性能

Fig.6 Noise suppression performance

Sobel水平、垂直、＋45°、－45°方向梯度算子（一阶梯度算子、加权平均）：

Prewitt水平、垂直、＋45°、－45°方向梯度算子（一阶梯度算子、取平均）：

Krisch梯度算子（相邻卷积核45°夹角）：

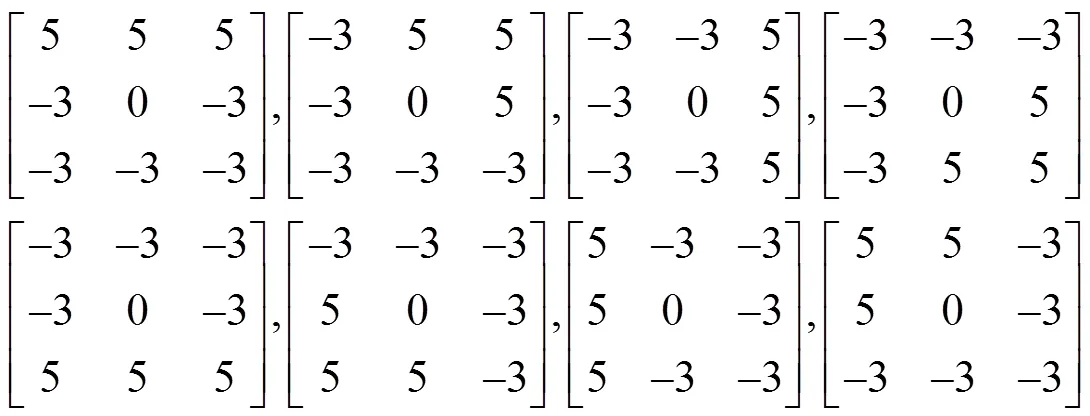
由图7可以看出，对主体水平边缘丰富的制冷红外图像，单个方向梯度算子，垂直方向对焦失败，“Prewitt算子函数——水平＋垂直”将图像与Prewitt水平和垂直方向算子分别卷积后取绝对值相加，“二阶垂直梯度算子——间隔一个像素-水平＋垂直”将图像与二阶水平、垂直方向梯度算子（间隔一个像素）分别卷积后取绝对值相加，SML函数将图像与二阶水平、垂直方向梯度算子分别卷积后取绝对值相加，这3种函数都修正了垂直方向的对焦偏差。基于拉普拉斯4邻域算子取梯度绝对值的函数性能与SML函数接近，“Prewitt水平＋垂直梯度算子”将Prewitt水平方向梯度算子和垂直方向梯度算子相加（试图构造类似拉普拉斯4邻域算子式的同时包含水平和垂直两个方向梯度信息的算子，实际得到的是Sobel －45°方向梯度算子）后与图像卷积，取梯度绝对值累加得到评价值，对焦失败（但对偏移有一定的修正效果），再次说明同时包含两个方向信息的梯度算子设计困难，聚焦评价函数包含两个方向信息（相互垂直）有利于提升算法的准确性。将拉普拉斯4邻域算子看作二阶水平、垂直方向梯度算子，由于两个方向梯度值可能符号不同，而SML函数相当于分开计算两个方向梯度后分别取绝对值相加，从上面的分析也看到两个互相垂直的梯度算子相加不一定得到一个包含两个垂直方向信息的算子。所以选用包含两个方向互相垂直的梯度算子分别于图像进行卷积后综合梯度信息的算法比单个梯度算子计算梯度的算法更可靠（注意到计算量大的基于Krisch梯度算子的函数性能并不是最好的，两个方向是合理的）。

从图8可以看出，绝对值和、模和、像素灰度值开平方根求梯度模和，计算量依次增加，但曲线性能十分接近，首选绝对值和。平方和函数相对于前面3种，曲线更加平滑，灵敏度提高。

从图9可以看出，梯度积和函数，Sobel和Prewitt算子对焦失败（图像对比度好时，间隔一个像素的二阶梯度计算效果不好），Roberts和SML算子对焦正确，两方向梯度乘积绝对值累加的方法并没有修正错误，最终评价函数分别在垂直和水平算子的定位点出现峰值，同时看到不同的算子阶数、方向信息和信息综合算法对同一组图像数据评价效果不同，这也是评价函数稳定性和通用性难以保证的原因。

图7 制冷红外图像两个梯度算子信息综合评价效果

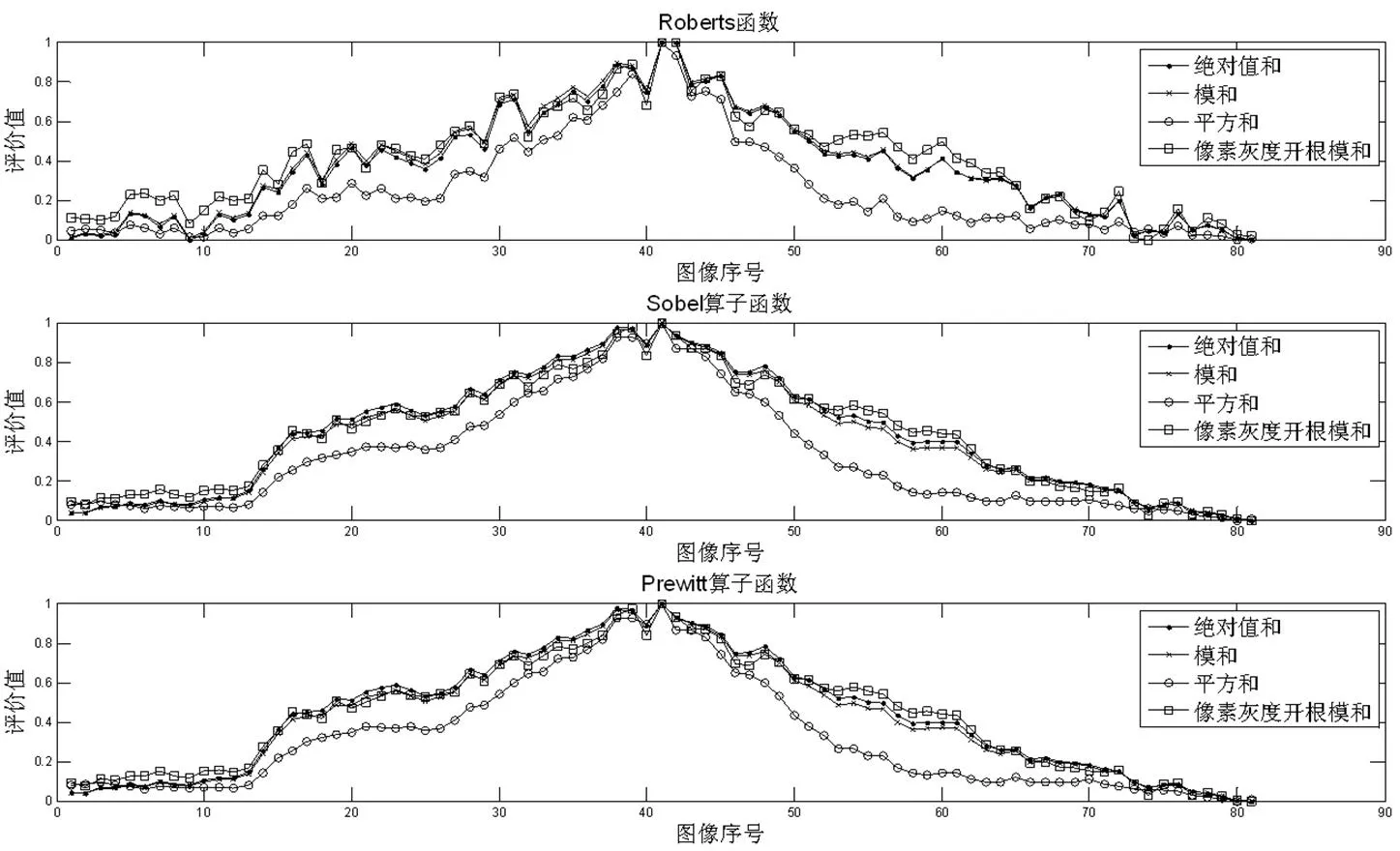
图8 制冷红外图像两个方向梯度信息综合的4种不同算子比较

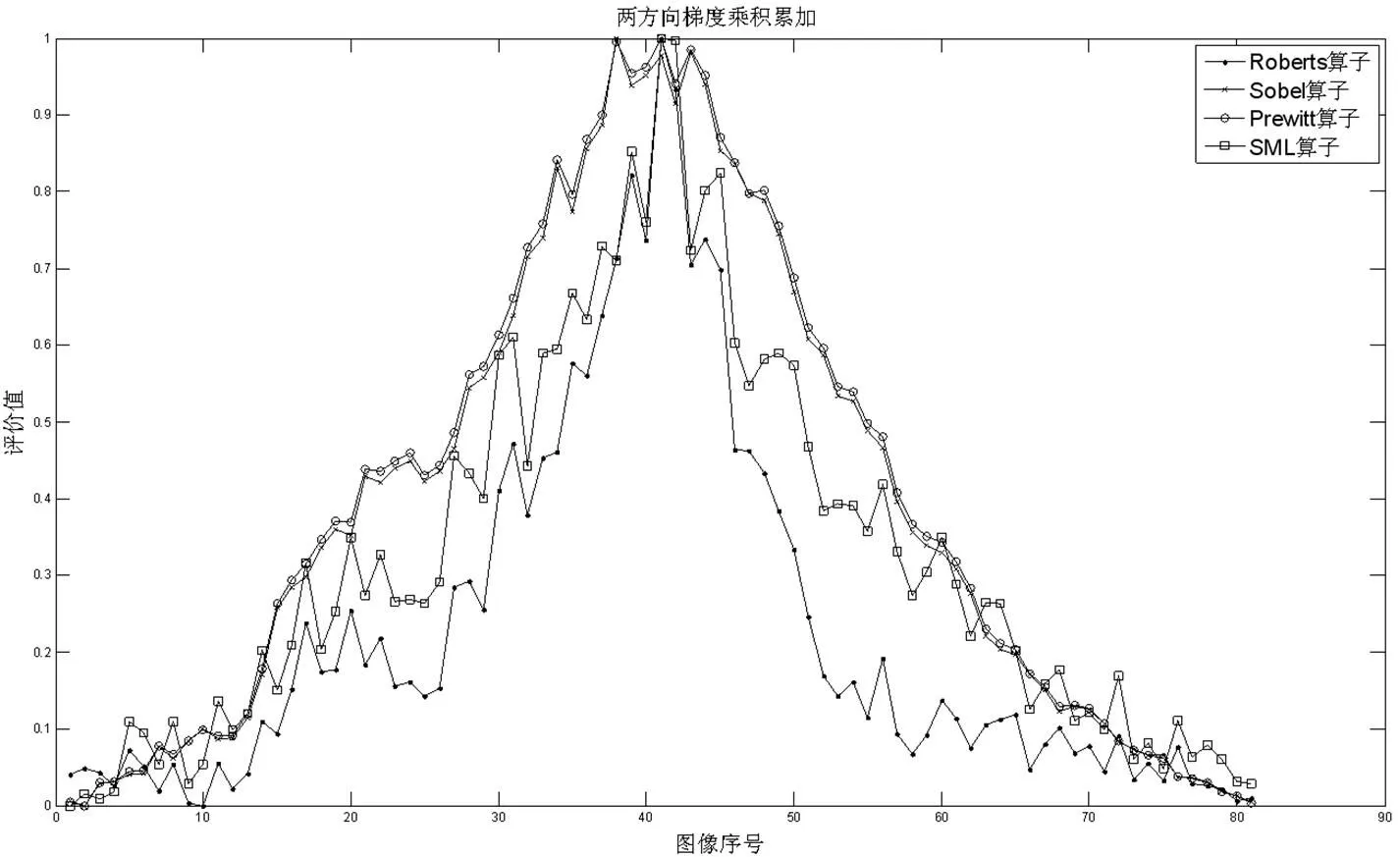
图9 制冷红外图像两个方向梯度信息综合

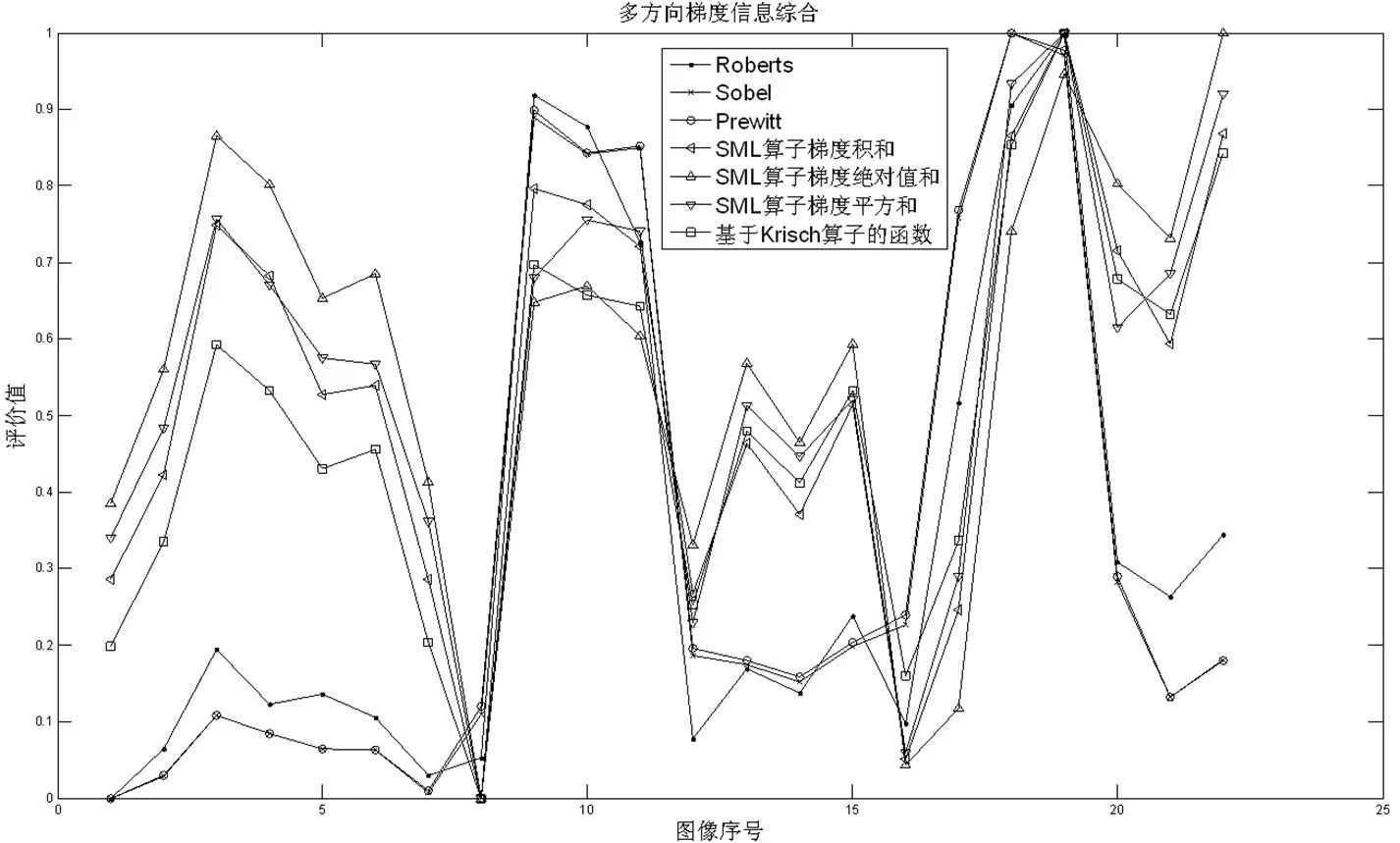
图10 非制冷红外图像两个方向梯度信息综合

从图10可以看出，对比度低的红外图像，Roberts算子（一阶）、Sobel、Prewitt算子（间隔一个像素计算梯度且做加权平均处理）准确对焦且很好地抑制离焦区的波动，而SML函数基于二阶水平和垂直梯度算子，3种综合方法都没有平滑函数曲线。图9显示，对角方向Roberts算子函数性能较好，对于对比度低的第二组图像，波动较间隔一个像素计算梯度的Sobel和Prewitt函数大，结合图5，再次说明间隔一个像素计算梯度处理对比度低的图像效果更好。

4 结论

单个梯度算子，不同的阶数、方向对不同纹理的图像敏感性不同，对比度高的图像，相邻像素计算梯度的算子较灵敏，通常二阶比一阶灵敏，对比度低的图像，相隔一个像素计算梯度的算子更灵敏；检测方向与实际边缘方向一致的算子对像质的评价更准确，同时检测水平和垂直方向的拉普拉斯4邻域算子较其他检测一个方向的算子更稳定、通用。

包含多个方向梯度算子的函数比单个梯度算子的函数对边缘的检测更全面，两个互相垂直方向比较合适，两个方向梯度绝对值和相加的处理方法在几种信息综合方法中计算量适中、性能也比较稳定。

梯度绝对值累加计算评价值的函数对高斯噪声和椒盐噪声抗扰性能较梯度平方累加的函数好，后者曲线的平滑性好，但对阈值依赖性大、计算量也较大。

针对具体的成像系统，根据图像对比度、常用场景特点，合理地设计梯度算子的方向、阶数及信息综合算法，进一步可分析评价函数的平滑处理，提升算法性能[17-18]。

[1] N Ng Kuang Chern, Poo Aun Neow, M H Ang. Pratical issues in pixel-based autofocusing for machine vision[C]//, 2001, 4: 10.1109/ ROBOT.2001. 93304.

[2] Gonzalez, R C, Woods R E.[M]. Third Edition: Publishing house of electronics industry, 2011.

[3] 徐贵力, 刘小霞, 田裕鹏, 等. 一种图像清晰度评价方法[J]. 红外与激光工程, 2009, 38(1): 180-184.

XU Guili, LIU Xiaoxia, TIAN Yupeng, et al. Image clarity-evaluation- function method[J]., 2009, 38(1): 180-184.

[4] 王健, 陈洪斌, 周国忠, 等. 改进的Brenner图像清晰度评价算法[J]. 2012, 41(7): 855-858.

WANG Jian, CHEN Hongbin, ZHOU Guozhong, et al. An improved Brenner algorithm for image definition criterion[J].a, 2012, 41(7): 855-858.

[5] 吴剑, 丁辉, 王广志, 等. 边缘检测微分算子的分析及在医学图像中的应用[J]. 生物医学工程学杂志, 2005, 22(1): 82-85.

WU Jian, DING Hui, WANG Guangzhi, et al. The frequency features and application of edge detection differential operators in medical image[J]., 2005, 22(1): 82-85.

[6] 黄亿, 王兴, 李辉. 一种新的高灵敏度聚焦评价函数[J]. 微计算机信息, 2009, 25(9): 163-165.

HUANG Yi, WANG Xing, LI Hui. A new kind of high-sensitive focus evaluation function[J].2009, 25(9): 163-165.

[7] 高赞, 姜威, 朱孔凤, 等. 基于Roberts 梯度的自动聚焦算法[J]. 红外与激光工程, 2006, 35(1): 117-121.

GAO Zan, JIANG Wei, ZHU Kongfeng, et al. Auto focusing algorithm based on Roberts gradient[J]., 2006, 35(1): 117-121.

[8] 李郁峰, 陈念年, 张佳成. 一种快速高灵敏度聚焦评价函数[J]. 计算机应用研究, 2010, 27(4): 1534-1536.

LI Yufeng, CHEN Niannian, ZHANG Jiacheng. Fast and high sensitivityfocusing evaluation function[J]., 2010, 27(4): 1534-1536.

[9] 邹昌帆, 刘秉琦, 黄富瑜, 等. 基于多向最大梯度阈值的自动调焦评价函数[J]. 激光与红外, 2016, 46(1): 115-118.

ZOU Changfan, LIU Binqi, HUANG Fuyu, et al. Automatic focusing evaluation function based on multi-directional maximal gradient threshold method[J]., 2016, 46(1): 115-118.

[10] 张来线, 孙华燕, 郭惠超, 等. 基于图像灰度梯度最大值累加的自动调焦算法[J]. 光子学报, 2013, 42(5): 605-610.

ZHANG Laixian, SUN Huayan, GUO Huichao, et al. Auto focusing algorithm based on largest gray gradient summation[J], 2013, 42(5): 605-610.

[11] 洪裕珍, 任国强, 孙健. 离焦模糊图像清晰度评价函数的分析与改进[J]. 光学精密工程, 2014, 22(12): 3401-3408.

HONG Yuzhen, REN Guoqiang, SUN Jian. Analysis and improvement on sharpness evaluation function of defocused image[J]., 2014, 22(12): 3401-3408.

[12] 蒋婷, 谭跃刚, 刘泉, 等. 基于SOBEL算子的图像清晰度评价函数研究[J]. 计算机与数字工程, 2008, 226(8): 129-131.

JIANG Ting, TAN Yuegang, LIU Quan, et al. Research of a clarity-evaluation function of image based on sobel[J]., 2008, 226(8): 129-131.

[13] 杜奇, 向健勇, 袁胜春. 基于边缘强度的红外图像阈值分割方法研究[J]. 红外与激光工程, 2004, 33(3): 288-291.

DU Qi, XIANG Jianyong, YUAN Shengchun. Sudy on thresholding segmentation for infrared image based on edge detection[J]., 2004, 33(3): 288-291.

[14] 张宏飞, 亚涛, 刘志广. 基于梯度阈值计数的清晰度评价算法[J]. 科学技术与工程, 2013, 34(13): 10365-10367.

ZHANG Hongfei, ZHANG Yatao, LIU Zhiguang. Focus-evaluation algorithm based on gradient threshold count[J]., 2013, 34(13): 10365-10367.

[15] 王倩, 宋恩民, 许向阳, 等. 基于加权邻域相关性的显微镜自动聚焦函数[J]. 光学精密工程, 2008, 16(1): 166-171.

WANG Qian, SONG Enmin, XU Xiangyang, et al. Auto-focusing function for microscope image based on weighted neighborhood correlation[J]., 2008, 16(1): 166-171.

[16] 赵春江, 施文康, 邓勇. 新的梯度边缘检测方法[J]. 光电工程, 2005, 32(4): 86-88.

ZHAO Chunjiang, SHI Wen-ang, DENG Yong. Novel edge detection method based on gradient[J]., 2005, 32(4):86-88.

[17] 倪军, 袁家虎, 吴钦章. 基于边缘特征的光学图像清晰度判定[J]. 中国激光, 2009, 36(1): 172-176.

NI Jun, YUAN Jiahu, WU Qinzhang. Identification for optical image definition based on edge feature[J]., 2009, 36(1): 172-176.

[18] 任四刚, 李见为, 谢利利. 基于灰度差分法的自动调焦技术[J]. 光电工程, 2003, 30(2): 53-55.

REN Sigang, LI Jianwei, XIE Lili. Automatic focusing technique based on gray scale difference method[J]., 2003, 30(2): 53-55.

Simulation Analysis of Auto Focusing Sharpness Evaluation Function for Images Based on Gradient Operator

PAN Xuejuan1,2，ZHU Youpan1,2，PAN Chao1，HAN Juan1，LI Daqing3，ZHANG Hao1，LUO Lin1，LI Zemin1

Kunming Institute of PhysicsKunmingChinaScience and Technology on Low-light-level Night Vision LaboratoryXianChinaUnitof PLA, BeijingChina

Image sharpness evaluation function based on gradient calculation is widely used in automatic focus system, and these functions vary in form. In this paper, starting from the mathematical principles of image gradient calculation, with simulation experiments under MATLAB, performance of common gradient class evaluation functions was compared and analyzed, and methods combining the characteristics of imaging system to control the performance of these algorithms are presented.

gradient operator，evaluation function，mathematical principles，auto focus，MATLAB

TP391.41，TP242

2016-08-30；

2016-09-28.

潘雪娟（1990-）女，硕士研究生，研究方向为图像处理，E-mail：1531796807@qq.com。

朱尤攀（1978-）男，研究员级高级工程师，博士研究生，研究方向为光电成像系统，E-mail：zhuypbit@aliyun.com。

A

1001-8891(2016)06-0960-08