浅谈数学中函数定义域优先问题
2016-03-27江西省丰城中学
江西省丰城中学 张 璐
浅谈数学中函数定义域优先问题
江西省丰城中学 张 璐
思维品质是指个体思维活动特殊性的外部表现。它包括思维的严密性、思维的灵活性、思维的深刻性、思维的批判性和思维的敏捷性等品质。函数作为高中数学的主线,贯穿于整个高中数学的始终。
函数关系式 函数最值 函数值域 函数单调性 函数奇偶性
一、函数关系式与定义域
函数关系式包括定义域和对应法则,所以在求函数的关系式时必须要考虑所求函数关系式的定义域,否则所求函数关系式就可能是错误的。如:
例1:某单位计划建筑一矩形围墙,现有材料可筑墙的总长度为100m,求矩形的面积S与矩形长x的函数关系式?
解:设矩形的长为x米,则宽为(50-x)米,由题意得:S=x(50-x),
故函数关系式为:S=x(50-x).
如果解题到此为止,则本题的函数关系式还欠完整,缺少自变量x的范围。也就是说学生的解题思路不够严密。因为当自变量x取负数或不小于50的数时,S的值是负数,即矩形的面积为负数,这与实际问题相矛盾,所以还应补上自变量x的范围:0 即:函数关系式为:S=x(50-x)(0 函数的值域是该函数全体函数值的集合,当定义域和对应法则确定,函数值也随之而定。因此在求函数值域时,应注意函数定义域。如: ∴y=2(t2+3)-5+t=2t2+t+1 剖析:经换元后,应有t≥0,而函数y=2t2+t+1在[0,+∞)上是增函数, 所以当t=0时,ymin=1. 故所求的函数值域是[1,+∞). 函数单调性是指函数在给定的定义域区间上自变量增加时,函数值随着增减的情况,所以讨论函数单调性必须在给定的定义域区间上进行。 判断函数的奇偶性,应先考虑该函数的定义域区间是否关于坐标原点成中心对称,如果定义域区间关于坐标原点不成中心对称,则函数就无奇偶性可谈。否则要用奇偶性定义加以判断。 综上所述,在求解函数关系式、最值(值域)、单调性、奇偶性等问题中,若能精细地检查思维过程,思辨函数定义域有无改变(指对定义域为R来说),对解题结果有无影响,就能提高学生质疑辨析能力,有利于培养学生的思维品质,从而不断提高学生思维能力,进而有利于培养学生思维的创造性。二、函数值域与定义域
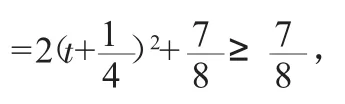
三、函数单调性与定义域
四、函数奇偶性与定义域
