变速调节对离心泵泥沙磨损特性的影响分析

董 静，钱忠东，郭志伟，王志远

(武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

双吸式离心泵具有流量大、扬程高的特点，被广泛用于引黄灌区，水泵设计时一般以清水作为工作介质。在输送含沙水流过程中，由于泥沙颗粒的存在，会对过流部件产生严重的冲蚀磨损[1]，使泵结构材料受到破坏，造成离心泵出水流量减少、抗汽蚀性能恶化[2]、装置效率降低，严重危害水泵的安全和稳定运行。含沙水流实质上是固液两相流，国内外已经有大量文献对离心泵内固液两相流的流动特性进行了相关研究[3-8]，对过流部件的磨损机理进行了探索[9-13]，并提出了相应的抗磨损方案[12,13]。许洪元等[8]利用高速摄影对离心泵叶轮中固体颗粒运动规律进行了试验研究，并与数值计算结果作了比较，结果表明，固体颗粒的密度、粒径、叶轮的转速和叶片角对颗粒运动均有明显影响。刘娟等[9]对离心泵内固相颗粒的运动轨迹及过流部件表面的磨损状态进行了数值模拟，发现固体颗粒的性质和叶轮的转速对颗粒运动轨迹及与壁面的碰撞过程有重要影响。钱忠东等[12]研究了不同叶片头部形状对泥沙磨损的影响，发现叶片磨损强度受相对流速分布和冲击角的影响。可见，通过变速调节，改变叶轮内相对流速分布，可改善水泵泥沙磨损现状。

近年来，CFD技术对水泵性能预测的结果已达到工程应用精度[14-16]。本文采用欧拉-拉格朗日多相流模型，对双吸式离心泵内的水流和泥沙颗粒运动进行了模拟，运用离散相冲击磨损模型计算过流部件的泥沙磨损强度，并对设计工况和变转速工况下的叶轮磨损情况进行对比和分析。

1 物理模型及数值计算方法

1.1 几何模型

计算采用的双吸式离心泵参数为：设计流量Qd=1 746 m3/h，设计扬程Hd=73.7 m，额定转速n=970 r/min，叶轮叶片数Z=6，转轮直径D= 780 mm。计算全流道模型如图1所示，计算区域包括：吸水室、叶轮、压水室及出水管部分。图2为离心泵叶轮三维模型图。由于双吸式离心泵结构较为复杂，因此采用对复杂外形适应性更好的非结构化网格对计算区域进行离散。

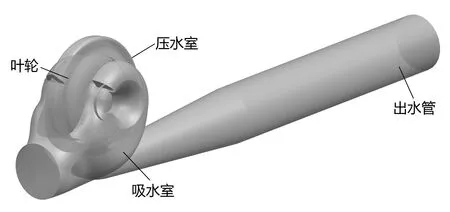
图1 双吸式离心泵三维模型图Fig.1 3D perspective view of the centrifugal pump

图2 双吸式离心泵叶轮三维模型图Fig.2 3D perspective view of the impeller

1.2 控制方程

基于黏性不可压缩雷诺时均N-S方程[17]，考虑到双吸式离心泵中存在强烈的旋流，本文选择对强旋度适应性更好的RNGk-ε湍流模型[18,19]进行数值模拟。

在欧拉-拉格朗日多相流模型中，颗粒运动方程为：

(1)

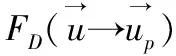
欧拉-拉格朗日多相流模型集中了宏观拟流体模型和微观动力学模型的优点，不仅可以反映固液两相之间的相互作用，而且可以描述颗粒之间的相互碰撞。泥沙对过流部件的离散相冲击磨损模型为:

(2)

1.3 计算方法与边界条件

运用有限体积法对控制方程进行离散，压力-速度耦合求解采用SIMPLEC算法，旋转区域和非旋转区域采用多重坐标系，对双吸式离心泵内的水流和泥沙颗粒运动进行计算。进口断面给定质量流量进口，出口断面设为压力出口边界，固壁为无滑移边界条件。

2 计算结果与分析

2.1 设计工况下叶轮磨损结果与分析

为了验证模型和计算方法的可靠性，通过离心泵的流量和扬程等外特性的计算值与实测值之间的比较进行验证。本文计算给定进口流量，计算扬程为75.6 m，误差为2.6%，计算值与实测值吻合很好，说明本文采用的模型和计算方法是可靠的。根据泵站运行时泥沙记录，选取粒径D=0.12 mm，浓度C=10 kg/m3的泥沙颗粒进行磨损计算。

图3为叶片及轮毂面泥沙磨损强度分布图。从图3(a)和图3(b)可以看出，设计工况下，叶片吸力面的磨损强度大于压力面，磨损主要集中在叶片进口边附近以及吸力面出口边与盖板相接的区域。从图3(c)可以看出，轮毂面出现较大面积的磨损，磨损主要分布在叶片进口附近以及轮毂面上靠近叶片吸力面的区域，磨损强度最大的位置在轮毂面靠近叶片吸力面的区域。

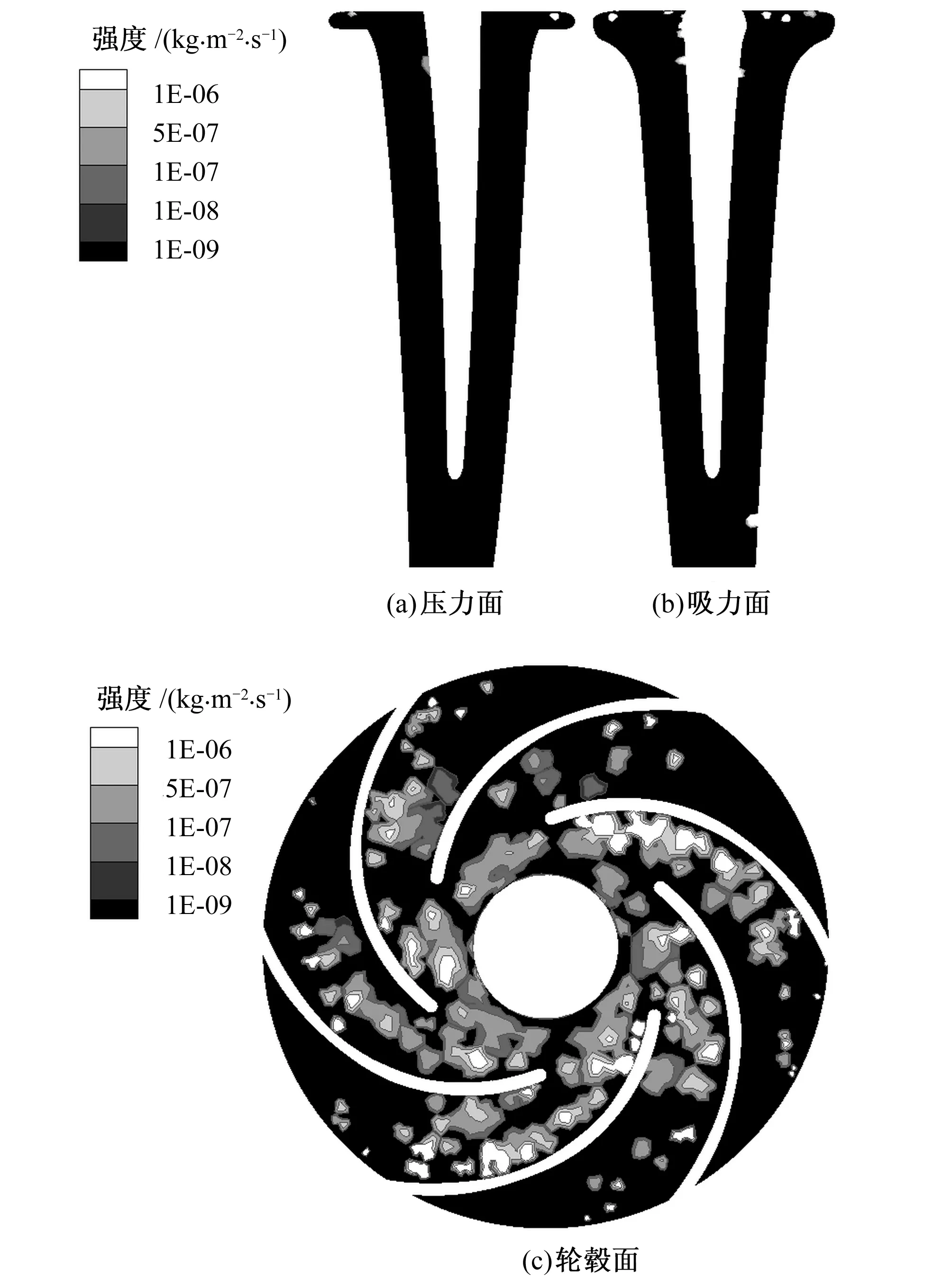
图3 叶片及轮毂表面磨损强度分布图Fig.3 Erosion rate on the blade and hub surfaces

图4为原型泵磨损后的叶轮，叶片头部出现锯齿状深坑，轮毂面靠近叶片吸力面的区域出现穿孔，实际磨损部位与本文预测的高强度磨损位置基本一致，表明本文采用的数学模型是可靠的。

图4 原型泵叶轮磨损实物图Fig.4 Photo of the wear pattern of the prototype runner

图5为叶片附近相对流速分布图。由图5可知，吸力面附近的相对流速明显大于压力面。压力面附近的相对流速从进口到出口，总体上先减小后增大，出口边附近的相对流速较高，在靠近叶片中间段出现低速区[16]。吸力面进口边相对流速高且分布极不均匀，受到较强的冲击作用[17]，但吸力面中间段和出口附近相对流速大小基本一致，且分布均匀。图6为轮毂面附近相对流速分布图。可以看出，轮毂面附近相对流速分布很不均匀，在叶片进口边附近相对流速最大，吸力面相对流速高于压力面，压力面中间段附近相对流速较低。

图5 叶片表面相对流速分布图Fig.5 Relative velocity field on blade surface

图6 轮毂面相对流速分布图Fig.6 Relative velocity field on the hub surface

2.2 提高机组运行转速后叶轮磨损结果与分析

结合现场叶轮磨损情况和数值模拟结果可知，磨损主要集中在叶片头部以及轮毂面靠近叶片吸力面附近的区域，其原因主要是叶片进口处流体对叶片的冲角不合理，相对流速分布不均匀。由于局部磨损发展最快，危害最大[18]，为了延长水泵在含沙条件下的运行寿命，本文旨在降低泥沙局部磨损强度，分散磨损区域，从而减缓叶轮局部磨损速度。据此，本文提出通过适当提高机组运行转速，调节水泵运行工况点，改善叶轮内部流场，来改善叶轮磨损现状。

由于缺乏叶轮外特性资料，故参考离心泵转速调节的一般规律对流量进行预估计算，如图7所示调节到工况点3，使机组扬程不低于调整前即可满足现场使用需求。由于提高转速会增加叶轮的受力并降低水泵汽蚀性能，因此在本研究中，仅将转速提高了约3%。在数值模拟试验中将叶轮转速设置为1 000 r/min。经试算最终确定以流量为2 000 m3/h进行数值模拟。

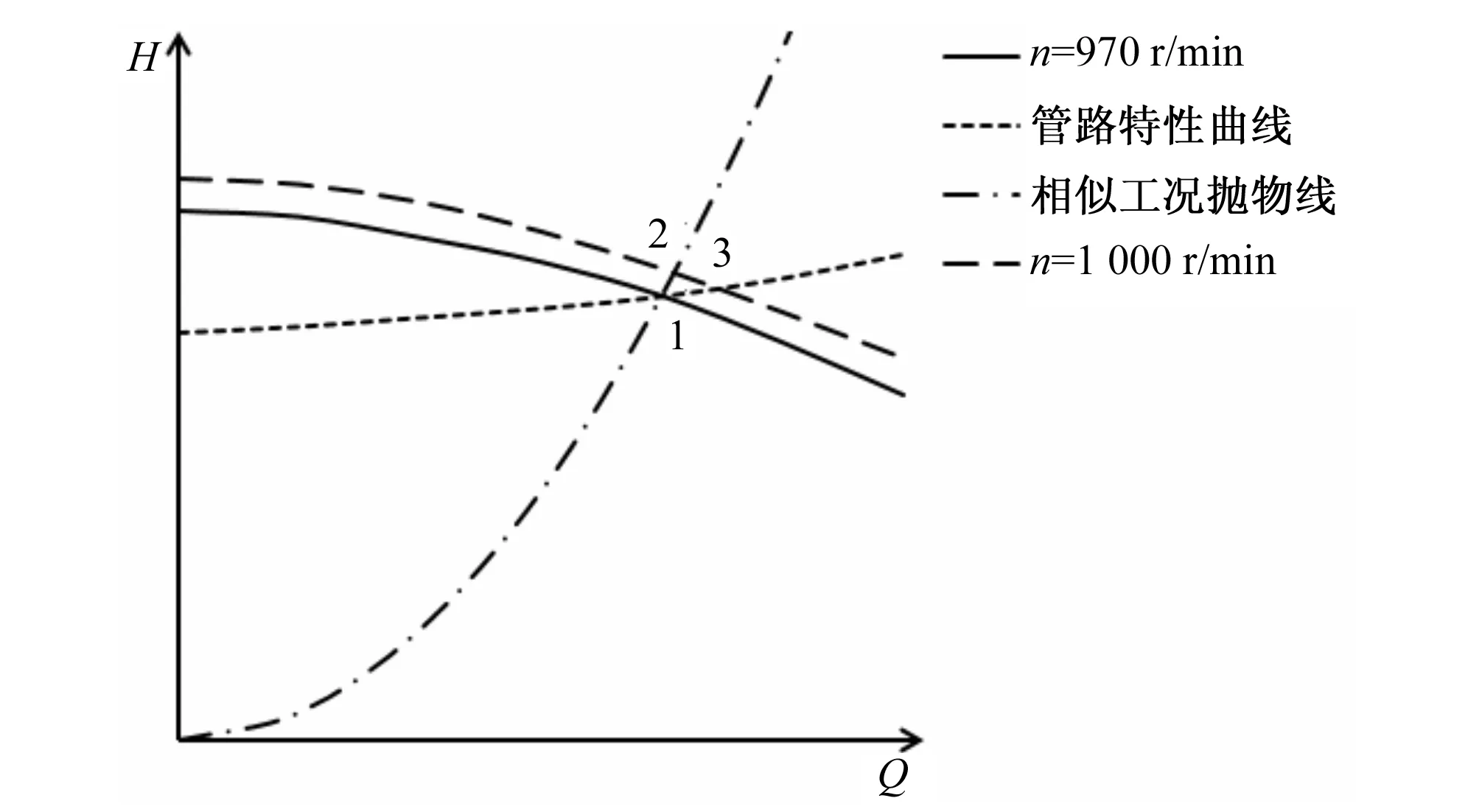
图7 变速调节工作点示意图Fig.7 Sketch of variable speed regulation

提高转速后，叶片与轮毂磨损结果如图8所示。将计算结果与设计工况下的磨损情况进行对比可知，提高机组运行转速后，叶片和轮毂面磨损情况得到明显改善。压力面进口边附近较高强度的磨损消失；吸力面进口边附近高强度磨损区域明显减小，出口段外缘侧的磨损位置向出口边中间位置移动。轮毂面上磨损明显改善，磨损区域变得分散，靠近吸力面附近的高强度磨损面积明显减小。

图9为提高机组运行转速后，叶片附近相对流速分布图。将图9与图5对比分析可知，提高机组运行转速后，叶片表面的相对流速均有所提高。压力面中间段的低流速区的范围大幅度减小，出口边附近的相对流速变大；吸力面靠近进口边附近的相对流速最大值变小，分布更加均匀。图10为提高机组运行转速后，轮毂面相对流速分布图，可知，轮毂面上相对流速分布更加均匀，良好的流态可改善颗粒对壁面的冲击作用，从而有效降低泥沙对过流部件的集中磨损，使叶片和轮毂表面磨损严重的位置变得分散，磨损面积明显减小。

图8 叶片及轮毂表面磨损强度分布图 (n=1 000 r/min)Fig.8 Erosion rate on the blade and hub surfaces

图9 叶片表面相对流速分布图(n=1 000 r/min)Fig.9 Relative velocity field on blade surface

图10 轮毂面相对流速分布图(n=1 000 r/min)Fig.10 Relative velocity field on the hub surface

3 结 语

(1)设计工况下，叶轮磨损严重位置主要集中在叶片头部以及轮毂面上靠近叶片吸力面附近的位置，数值模拟结果与现场磨损情况吻合良好。

(2)设计工况下，叶片进口处流体对叶片的冲角不合理，相对流速分布不均，使叶片进口边及轮毂面出现较高强度的集中磨损。

(3)提高水泵运行转速后，叶轮流道中相对流速分布变均匀，改善了泥沙颗粒对叶片和轮毂表面的磨损。

□

[1] 顾四行. 减轻抽黄引水工程水泵泥沙磨损的有效途径[J]. 水泵技术，2010,(1)：1-4.

[2] 张 涛，陈次昌，郭 清. 含沙水流中翼型空蚀磨损试验[J]. 农业机械学报，2010，41(11)：31-37.

[3] Dunstana P J, Li S C. Cavitation enhancement of silt erosion: numerical studies[J]. Wear, 2010(268):946-954.

[4] Liu Jianhua, Zhu Mingyi. Numeration simulation of solid-liquid two phase flow in centrifugal sewerage pump[J]. Applied Mechanic and Materials, 2011,(44-47):345-348.

[5] Zhang Y L, Li Y, Cui B L, et al. Numerical simulation and analysis of solid-liquid two-phase flow in centrifugal pump[J]. Chinese Journal of Mechanical Engineering, 2013,26(1):53-60.

[6] Wu B, Wang X L, Liu H, et al. Numerical simulation and analysis of solid-liquid two-phase three-dimensional unsteady flow in centrifugal slurry pump[J]. Journal of Central South University, 2015(22):3 008-3 016.

[7] Huang Si, Su Xianghui, Qiu Guangqi. Transient numerical simulation for solid-liquid flow in a centrifugal pump by DEM-CFD coupling[J]. Engineering Applications of Computational Fluid Mechanics, 2015,9(1):411-418.

[8] 许洪元，吴玉林，高志强，等. 稀相固粒在离心泵轮中的运动实验研究和数值分析[J]. 水利学报，1997，(9)：12-18.

[9] 刘 娟，许洪元，唐 澎，等. 离心泵内固体颗粒运动规律与磨损的数值模拟[J]. 农业机械学报，2008，39(6)：54-59.

[10] Yang C X, Dong F D, Cheng X R. Numerical investigation of sediment erosion to the impeller in a double-suction centrifugal pump[C]∥6th International Conference on Pumps and Fans with Compressors and Wind Turbines. Tsinghua Univ, Beijing, PEOPLES R CHINA, 2013.

[11] 陶 艺，袁寿其，张金凤，等. 渣浆泵叶轮磨损的数值模拟及试验[J]. 农业工程学报，2014，30(21)：63-69.

[12] Qian Z D, Wang Z Y, Zhang K, et al. Analysis of silt abrasion and blade shape optimization in a centrifugal pump[J]. Journal of Power and Energy, 2014,228(5):585-591.

[13] Qian Z D, Gao Y Y, Zhang K, et al. Influence of dynamic seals on silt abrasion of the impeller ring in a centrifugal pump[J]. Journal of Power and Energy, 2013,227(5):557-566.

[14] Shukla S N, Kshirsagar J T. Numerial experiments on a centrifugal pump[J]. American Society of Mechanical Engineers, Fluids Engineering Division( Publication) FED, 2002,257(2B):709-720．

[15] 任 涛，闫永强，梁武科. CFD技术在离心泵优化设计中的应用[J]. 排灌机械，2007，25(1)：25-28.

[16] 郎 涛，施卫东，陈刻强，等. 不同比转数前伸式双叶片离心泵内部流动规律研究[J]. 农业机械学报，2015，46(12)：89-95.

[17] 窦华书，蒋 威，张玉良，等. 基于能量梯度理论的离心泵内流动不稳定研究[J]. 农业机械学报，2014，45(12)：88-103.

[18] 关醒凡. 现代泵理论与设计[M]. 北京:中国宇航出版社,2010.