南海简正模态型季节内振荡的数值模拟❋

朱聿超， 赵小龙， 赵　玮

(中国海洋大学物理海洋实验室， 山东 青岛 266100)



南海简正模态型季节内振荡的数值模拟❋

朱聿超， 赵小龙， 赵玮❋❋

(中国海洋大学物理海洋实验室， 山东 青岛 266100)

摘要：本文基于大洋环流数值模式HYCOM对南海季节内振荡进行模拟，并利用CEOF方法对季节内振荡的物理特性进行了分析。结果表明，季节内振荡起源于南海东边界并以5.87cm·s-1向西传播，在南海海盆内存在3个完整波型，波长为360km，周期为71d。季节内振荡引起的流速振幅在表层最大，随着深度的增加迅速减小。Rossby波理论的分析结果表明,该振荡是南海海盆内的简正模态，属于Rossby波的第一斜压模态。

关键词：南海； 第一斜压Rossby波； 复经验正交函数

ZHU Yu-Chao, ZHAO Xiao-Long, ZHAO Wei. The intraseasonal basin normal mode in South China Sea envisioned from HYCOM[J]. Periodical of Ocean University of China, 2016, 46(2): 1-5.

南海是西北太平洋最大的边缘海，平均水深大于1 000m，最大水深超过5000m，主要通过吕宋海峡、台湾海峡、民都洛海峡等与周围海区进行水体交换。其中吕宋海峡水深超过2000m，是连接南海与太平洋的唯一深水通道。

南海地处东亚季风区，季风是海洋上层环流的主要驱动力。利用早期水文观测、海表面高度记录，Wyrtki[1]首先给出南海表层环流结构：在冬季，南海海盆呈现气旋型环流；在夏季，南海南部出现反气旋型环流。对于深层，Tian等[2]在吕宋海峡的观测表明，南海1000m以下的垂向混合率高于太平洋一侧2个数量级。南海深层的强混合导致太平洋水密度更大，由此产生的水平压强差驱动了从太平洋到南海的深层溢流。太平洋深层水通过巴士海峡进入南海后，在深层形成水平气旋型的环流[3-4]。在南海内区强混合的作用下，深层水上升并在垂直方向上形成南海深层径向翻转流。由于缺乏直接观测，温盐诊断与数值模拟是研究南海深层环流的主要手段[4-8]。

季节内振荡对流场的变异有非常重要的影响：WOCE计划对马斯克林海盆进行了2年的海流观测，发现流场存在显著的季节内振荡，周期为60d，流速振幅达到10cm·s-1。振荡信号以7.0cm·s-1的相速度向西传播，符合正压Rossby波的特征[9]；北大西洋深层西边界流的观测结果表明流场存在以40d为周期的季节内振荡，地形Rossby波是造成振荡的原因[10]。由于观测资料的匮乏，对于南海季节内振荡的研究主要集中在中上层。Zhuang等[11]结合卫星高度计与OFES模式资料，对南海海表面高度的季节内振荡进行了研究：在南海北部陆架区及越南东侧海域分别存2个强季节内振荡区域，振荡周期约为10周，西传Rossby波是产生季节内振荡的原因之一。Zheng等[12]利用2007年与2009年夏季航次获得的CTD资料，发现南海内部存在3个沿纬向的完整波型。Zhang等[13]基于1年的潜标观测数据，发现在吕宋海峡中层存在周期为10～30d和60d的季节内振荡，并且与上层的季节内振荡呈现负相关关系。

地形与纬度、层结、几何形状共同决定了封闭海盆内的简正模态[14]，而南海海盆内的简正模态具有季节内振荡的特征[12]。本文基于HYCOM(Hybrid Coordinate Ocean Model)模式并结合现有的观测结果，对南海简正模态引起的季节内振荡进行研究。

1模式设置及分析方法

本文对季节内振荡进行模拟时采用了与Zhao等[5]相同的模式设置。模式计算区域包括整个南海及部分西北太平洋区域(4°N～25°N，105°E～125°E，见图1)。模式水平分辨率为1/12(°)，垂向分为32层，采用2000m处参考压强，目标位势位密依次为28.10，28.90，29.70，30.50， 30.95，31.50，32.05，32.60，33.15，33.70，34.25，34.75，35.15，35.50，35.80，36.04，36.20，36.34，36.46，36.56，36.64，36.70，36.74，36.78，36.82，36.84，36.86，36.88，36.92，36.96，37.01和37.06kg·m-3。模式采用GDEM3温盐数据作为初始场，鉴于Tian等[2]在吕宋海峡的观测，本文将南海1000m以下垂向混合率设为10-3m2·s-1。外强迫不是影响海盆内简正模态的因素，因此忽略海表面强迫，东边界采用温盐松弛边界条件，其它边界均为闭边界。模式在5年之后达到稳定状态，因此本文采用5～10a的模式结果进行分析。

通过经验正交函数(EOF)方法可将随时间变化的变量场分解为不随时间变化的空间函数部分与只依赖时间变化的时间函数部分。传统EOF分解获得的是空间驻波结构，不能刻画西传Rossby波。因此，本文采用复EOF(CEOF)方法对模式流场进行分析。CEOF方法是把实数随机向量，利用Hilbert变换后作为虚部构成复值随机向量。对复值随机向量进行EOF分解，得到的结果不仅反映出状态变率，还会反映出在相同时间上状态的空间变化。具体原理可参见Barnett[15]的工作。

图1　模式计算区域地形

2模式结果

根据Barnett[15]的经验，应用CEOF方法分析波动时，需要先对原始变量场进行适当的滤波。为了选取合适的带通频段，作者先对卫星高度计获得的海表面高度异常(Sea level anomaly, SLA)资料进行分析。文中所用的SLA数据来于法国AVISO(Archiving, Validation and Interpretation of Satellite Oceanographic Data)项目,该数据融合了TOPEX/Poseidon,ERS-1/2等多种卫星测高数据，空间分辨率为25km，时间分辨率为7d。本文利用1992—2013年的SLA数据，分别计算振荡周期在 8～120d(见图2(a))，40～80d(见图2(b))，14～40d(由于采样间隔为7d，可分辨最小周期为14d，(见图2(c))之间的能量比例。

(选择的频段为2π/120 ～2π/80d(a)、2π/80 ～2π/40d(b)and 2π/40 ～2π/14d(c)。The selected frequency bands are 2π/120 ～2π/80 d (a), 2π/80 ～2π/40 d (b) and 2π/40 ～2π/14 d (c).)

图2不同频段内谱能量百分比

Fig.2The spectrum percentage between a selected frequency band

从图2可以看出80～120d周期振荡在南海北部的能量比例可以达到30%，在其余海域的能量比例在20%以下；40 ～80d周期振荡的能量比例最大，在中央深水区的能量比例可以达到70%；14 ～40d周期振荡在南海北部陆架区、泰国湾内的能量比例可以达到60%以上，但在南海内区的能量比例很低。虽然SLA反应的季节内振荡可能与大气强迫有密切的关系，但大气强迫如果与简正模态具有相同的频率，会通过共振机制将此频率的信号增强[9]。因此先假设40～80d是本文所关心的振荡周期，把带通滤波后流速数据进行CEOF分解。选取14°N断面的结果进行CEOF分解，展示其垂向结构与传播特性。CEOF分解后可获得第一模态的时间相位函数与时间振幅函数(见图3(a))、空间相位函数(见图4(a))与空间振幅函数(见图4(b))。第一模态方差贡献率为41.6%。

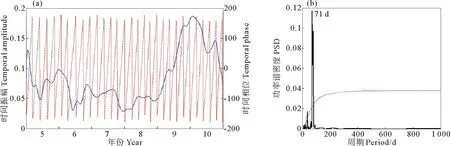
((a)蓝色实线为时间振幅函数，红色虚线为时间相位函数；(b)为时间函数的功率谱分析，其中红色虚线为95%置信度的显著性检验。(a) The solid blue line denotes the temporal amplitude value and doted red line denotes the temporal phase value between ±π in the left panel. (b) Represents the power spectral analysis for temporal phase function, and doted red line denotes the 95% significance test.)

图314°N断面径向速度的第一模态时间振幅函数与时间相位函数(a)与时间相位函数的功率谱密度(b)

Fig.3Temporal amplitude and temporal phase for first empirical mode of the meridional

velocities in Lat 14°N (a) and power spectral analysis for the temporal phase function (b)

通过时间振幅函数与时间相位函数可得到空间结构随时间的变化，并可以通过功率谱分析找到振荡的主要周期。本文对时间相位函数进行功率谱分析，发现其主要周期是71d(见图3(b))。

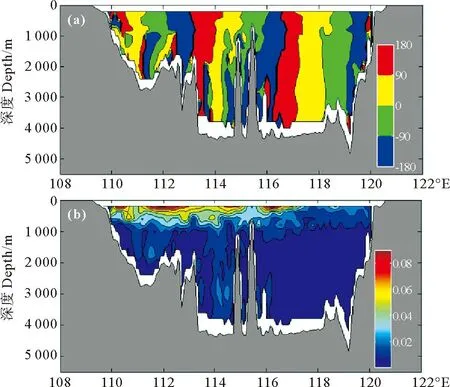
图4　14°N断面径向速度的第一模态空间相位

通过空间相位函数可以获得波动传播方向、波长等信息。从图4(a)可清晰看出，在南海深海盆内，波自东向西传播，纬向上存在3个完整波形，与Zheng[12]的观测结果相一致。同相位线的形态受地形影响较大。例如在114°E～116°E之间地形变化剧烈，1000m以下同相位线发生扭曲；在116°E～118°E之间地形平坦，同相位线呈现垂直状。根据空间振幅函数可以分析流速振幅的空间分布。从图4(b)可以看出，上层流速振幅明显大于下层，流速振幅的最大值出现在南海西边界附近，1 000m以下振幅变得很小，变化较微弱。上述结果表明，波动存在垂向结构，与Rossby波的第一斜压模态相似。将时间振幅函数与空间振幅函数相乘可以计算出振荡引起的流速变化。在表层，流速振幅可达到1.5cm·s-1，在1000m以下的深层，流速振幅只有mm·s-1量级。

14°N断面CEOF分解的结果表明，这种振荡是一种西传波动。为了描述波动的传播特性，本文选取500m深度处经向速度做CEOF分解(此处只描述其空间相位函数，见图5)，发现波动起源于南海东边界，同相位线基本与经线平行，表明波动主要是向西传播，只有在12°N以南以及中沙岛附近的海域，同相位线的形态受地形影响较大，发生了一定的扭曲。

通过上述分析得到了振荡的基本性质：振荡的生成源地是南海的东边界，以行波的形式向西传播；在南海海盆内存在3个完整波型；波动的周期为71d；波动引起的流速振幅在表层最大，随着深度的增加迅速减小。

图5　500 m深度径向速度第一模态空间相位函数

3讨论

南海可看作是封闭的海盆，在其内部激发的Rossby波存在水平结构。正如图5所示，在南海深海盆内存在3个完整的波形，封闭海区内存在准地转简正模态s，需要满足海盆几何尺度是Rossby波长整数倍的条件[14]。在14°N断面，南海海盆宽度约为1080km，因此可得到纬向波长约为360km。

层结流体中激发的Rossby波会存在垂向结构，不同斜压模态对应着不同的Rossby变形半径，此处先验证n=1时第一斜压模的结果。无论层结的垂向结构如何，正压模态都可能存在，在这种情况下，变形半径会足够大以至于在频散关系中，与k2相比，1/R2较小而可以忽略。纬向波长约为360km，则k约为1.75×10-5m-1(见图5)。对于l的取值，因图5表明波动主要呈现向西传播的特性，所以本文在频散关系中忽略了与l有关的项。β在14°N取2.22×10-11s-1，计算获得正压周期为57d，计算结果明显小于71d的周期，与谱分析的结果并不一致，所以排除了正压Rossby波的可能性。对于R1的计算，本文借助WOA 09气候态温盐数据，采用WKB方法计算出南海第一斜压Rossby变形半径[16]。南海第一斜压Rossby变形半径空间变化较大，对于深海区域，变形半径在80～120km之间[17]，如果Rossby变形半径取100km，将这些参量带入频散关系后发现计算获得的周期为75d，这与谱分析获得的结果是非常接近的。所以可以确定，模式中获得的季节内振荡是Rossby波的第一斜压模态。

4结语与展望

本文利用HYCOM模式对南海环流进行模拟，模式输出流场中出现以71d为周期的季节内振荡。利用CEOF分析方法，证明西传第一斜压Rossby波是振荡产生的原因。波动在纬向上存在3个完整波型，水平波长为360km，对应的西传波速为5.87cm·s-1。通过对南海上升流与下沉流量级的分析，本文推测太平洋深层水通过吕宋海峡入侵南海后下沉，下沉流导致的位涡变化是波动产生的主要机制。以上的机制解释只是模式结果的初步探讨，在下一步工作中，需要对上升流与下沉流的空间分布进行进一步的研究。

参考文献：

[1]Wyrtki K. Physical oceanography of the Southeast Asian waters [J]. Scripps Institution of Oceanography, 1961.

[2]Tian J, Yang Q, Zhao W. Observation of enhanced diapycnal mixing in the South China Sea [J]. J Phys Oceanogr, 2009, 39: 3191-3203.

[3]Qu T, Girton J B, Whitehead J A. Deepwater overflow through Luzon strait [J]. J Geophys Res, 2006, 111: C01002. doi: 10. 1029/2005JC003139.

[4]Wang G, Xie S P, Qu T, et al. Deep South China Sea circulation [J]. Geophysical Research Letters, 2011, 38(5). 05601

[5]Zhao W, Zhou C, Tian J, et al. Deep water circulation in the Luzon Strait [J]. J Geophys Res, 2014, 119(2): 790-804.

[6]Dongliang Y. A numerical study of the South China Sea deep circulation and its relation to the Luzon Strait transport [J]. Actaoceanol Ogica Sinica, 2002, 21(2): 187-202.

[7]Lan J, Zhang N, Wang Y. On the dynamics of the South China Sea deep circulation [J]. J Geophys Res, 2013, 118(3): 1206-1210.

[8]Shu Y, Xue H, Wang D, et al. Meridional overturning circulation in the South China Sea envisioned from the high-resolution global reanalysis data GLBa0.08 [J]. Journal of Geophysical Research: Oceans, 2014, 119(5): 3012-3028.

[9]Warren B A, Whitworth T, La Casce J H. Forced resonant undulation in the deep Mascarene Basin [J]. Deep Sea Research, 2002, 49(7): 1513-1526.

[10]Pickart R S, Watts D R. Deep western boundary current variability at Cape Hatteras [J]. Journal of Marine Research, 1990, 48(4): 765-791.

[11]Zhuang W, Xie S P, Wang D, et al. Intraseasonal variability in sea surface height over the South China Sea [J]. J Geophys Res, 2010, 115: C04010. doi: 10. 1029/2009JC005647.

[12]Zheng Q, Hu J, Zhu B, et al. Standing wave modes observed in the South China Sea deep basin [J]. J Geophys Res, 2014, 119(7): 4185-4199.

[13]Zhang Z , Zhao W, Tian J, et al. Spatial structure andtemporal variability of the zonal flow in the Luzon Strait[J]. J Geophys Res Oceans, 2015, 120, doi: 10. 1002/2014JC010308.

[14]Pedlosky J. Geophysical Fluid Dynamics [M]. New York: Springer-Verlag, 1986：144-153.

[15]Barnett T P. Interaction of the monsoon and Pacific trade wind system at interannual time scales Part I: the equatorial zone [J]. Monthly Weather Review, 1983, 111(4): 756-773.

[16]Chelton D B, Deszoeke R A, Schlax M G, et al. Geographical variability of the first baroclinic Rossby radius of deformation [J]. J Phys Oceanogr, 1998, 28(3): 433-460.

[17]Cai S, Long X, Wu R, et al. Geographical and monthly variability of the first baroclinicRossby radius of deformation in the South China Sea [J]. Journal of Marine Systems, 2008, 74(1): 711-720.

[18]Chelton D B, Schlax M G. Global observations of oceanic Rossby waves [J]. Science, 1996, 276: 234-238.

责任编辑庞旻

The Intraseasonal Basin Normal Mode in South China Sea Envisioned from HYCOM

ZHU Yu-Chao, ZHAO Xiao-Long, ZHAO Wei

(The Lab of Physical Oceanography, Ocean University of China, Qingdao 266100, China)

Abstract:A general ocean circulation model HYCOM isdescribedto usein the modeling of the intraseasonal Basin Normal Mode in the South China Sea (SCS) and a notable intraseasonal oscillation derived from the velocity field is investigated. The Complex Empirical Orthogonal Function(CEOF) analysis is used to characterize the intraseasonal oscillation. The oscillation at a period of 71 days originates along the east boundary of SCS and propagates westward witha wavelength of 360 km, about one third of the basin width. Amplitude of the oscillation reaches its maximum at upper layer and decreases with increasing depth. By utilizing the WOA climatological dataset and Rossbywaves theories, we identified that the wave is first baroclinicRossby wave.

Key words:South China Sea; first baroclinic Rossby wave; complex empirical orthogonal function

DOI：10.6441/j.cnki.hdxb.20150109

中图法分类号：P731.21

文献标志码：A

文章编号：1672-5174(2016)02-001-06

作者简介：朱聿超 (1989-)，男，硕士生。E-mail：zhuyuchao-2008@163.com❋❋通讯作者：E-mail：weizhao@ouc.edu.cn

收稿日期：2015-04-02；

修订日期：2015-05-21

基金项目：❋ 国家重点基础研究发展计划项目(2014CB745003)；南海海洋环流形成变异机理及其气候效应项目(GASI-03-01-01-03)；国家自然科学基金重大研究计划项目(91028008)；国家自然科学基金项目(41176010；41176008)；中国科学院战略性先导科技专项(XDA11010202)；三亚深海科学与工程研究所项目(SIDSSE-201207)资助

引用格式：朱聿超， 赵小龙， 赵玮.南海简正模态型季节内振荡的数值模拟[J].中国海洋大学学报(自然科学版)， 2016, 46(2)： 1-5.

Supported by National Basic Reasearch Porogram of China(2014CB745003)；Formation，variations and climatic impacts of the circulation in the South China Sea(GASI-03-01-01-03)；National Natural Science Foundation of China(91028008)；National Natural Science Foundation of China(41176010；41176008)；Strategic Priority Research Program of the Chinese Academy of Sciences(XDA11010202)；Sanya Institute of Deep-sea Science and Engineering(SIDSSE-201207)