一种分布式环境下高效查询算法❋

王　宁，曲海鹏，范　令

(中国海洋大学信息科学与工程学院， 山东 青岛 266100)



一种分布式环境下高效查询算法❋

王宁，曲海鹏❋❋，范令

(中国海洋大学信息科学与工程学院， 山东 青岛 266100)

摘要：很多交互系统需要实时返回潜在的数据空间中最重要的前k条记录，即为top-k查询。当今大数据时代，面对海量更加复杂的数据，输出这种top-k记录是一个非常具有挑战性的问题。传统的方案主要采用基于阈值的方法，然而对分布式系统来说，这些方法是比较耗时的，并且需要巨大的通信量。随着网络流量的增加，这些问题会变得无法解决。本文提出了一种新颖的top-k算法PCMRA(Data Partitioning and COIT Indexing Top-k query Algorithm based on MapReduce)。该解决方案构造了预处理结构COIT(候选对象索引表)，并采用数据分割策略和并行编程框架MapReduce，一轮通信就可以完成top-k查询。此外本文还对算法给出了正确性证明和理论分析，并且实验表明该算法仅需要较小的空间开销和较短的时间代价，即可筛选出较少的候选对象，大幅度节约了计算和通信资源，并且算法具有良好的可扩展性。

关键词：top-k查询；COIT；数据分割； MapReduce

WANG Ning, QU Hai-Peng, FAN Ling. PCMRA: An efficient top-kalgorithm in distributed environment[J]. Periodical of Ocean University of China, 2016, 46(2): 138-145.

当今大数据时代，数据不仅数量大，而且类型更加复杂，这导致了对数据处理的需求越来越高[1]。传统的算法和数据库系统已经难以有效应对，因此大数据快速查询算法的研究成为热点，排名查询就是复杂查询中一种。

排名查询也被称为top-k查询，它为高效搜索问题提供了解决方案。top-k查询只检索k个最符合用户需求的对象，从而避免计算、存储大量的结果集。在传统的集中式数据库，分布式数据库，以及大数据环境下，top-k查询都已受到广泛的重视，在这些应用场景中，只计算输出k个“最好”的结果就已经足够了。如有许多应用，如网络搜索，信息检索，多媒体数据库，数字图书馆，数据挖掘和推荐系统，只需要查询前k个最好合乎要求的记录[2]。

对于确定数据库而言，根据数据库的类型又分为两大类。对于集中式数据库，学术界为解决top-k查询问题已经做了很多工作[3]，而对于分布式数据库，这个问题一直没能得到很好的解决。根据数据划分策略，top-k查询又可以分为两类[4]：一类数据是水平划分的，这和本文所研究的应用场景是完全不同的。另一类数据是垂直划分的。对于这类top-k查询，大多解决方案主要采用基于阈值的方法。TPUT[5]和Klee[6]算法就是这类算法的典型代表。这类算法是从集中式数据库的算法发展来的，主要针对单一数据库的，没有考虑分布式的环境，尽管改进，但是仍需要与服务器几轮往返开销才能完成查询[7]，比较费时，需要大量的通信。随着网络通信量的增加，top-k查询将更加难以处理。

此外，近年来，由于在很多新兴的应用，如传感器网络，基于位置的服务，以及数据集成等应用领域管理的信息往往是不确定的，为了处理数据的不确定性，概率数据库被广泛研究。随之概率数据库的top-k查询问题也吸引了广泛的研究兴趣。在定义不确定型数据模型的基础上，多种可能世界语义的top-k查询模型已经提出，包括U-Topk[9],U-kRanks[9],PT-k[10],Gobal-topk[11],以及Expected Rank queries[12]等，相应的算法也被大量的研究。

本文为了提高算法的并行度，引入了计算模型MapReduce[8]。MapReduce是一个并行编程模型，它主要是针对大规模数据。它为用户提供2个接口，方便用户编写一些自定义的代码来处理大规模数据。

为了可以快速、准确地完成top-k查询，本文针对确定数据库提出了一种高效的算法PCMRA。该算法需要预先构建候选对象索引表COIT，top-k查询的k值一般比较小，因此算法只需要维护有限的COIT记录，就可以完成绝大多数top-k查询。有限的数据记录节约了数据构建的成本以及占有的空间。数据一般分布在网络中不同的节点，并且通常每个服务器中只储存着一个或几个属性，而top-k查询涉及到同一个对象的多个属性的综合得分，这就需要不止一个服务器的参与才能完成计算。本文采用数据划分策略，减少了节点间的通信开销，这就使算法具有很高的可扩展性，随着数据量的增加，这种优势将更加明显。通过使用预构建数据结构COIT，我们的算法首先获取候选id集合，然后根据数据划分策略对候选id集合进行分组。在得到分组后的id集合后，借助并行编程模型MapReduce的开源实现平台Hadoop，只需一轮往返通信就可以完成top-k查询。

1算法介绍

1.1 问题描述

top-k查询：给定一个表T和一个单调的排名函数F，top-k查询返回表T的一个包含k条记录的子集R(k≤|T|))，满足条件∀ti∈R，∀tj∈[T-R]，则F(ti)≥F(tj)。表的关系模式为T(ID，A1，A2，……，Am)，表T中元组tj的各属性Ai都对应一个得分值，记为Tj.bsi。排名函数F=∑wi×Tj.bsi是单调的，即对于∀i，若存在1≤i≤m，xi≤yi，则F(x1，……，xm)≤F(y1，……，ym)，其中wi是对应属性Ai的权重，并且各属性权重和为1，即∑wi=1。

1.2 预处理结构

在收到top-k查询之前，为了实现算法，需要预先建立数据结构候选对象索引表COIT。COIT表是一种全局索引表，从中可以方便的查到各个k值以及各属性组合对应top-k查询的候选id集合，借助COIT来可以快速的完成排名查询。

全局索引表(COIT)：处理的数据对象是分布在不同数据源上的，每个数据源都是可以转换或者提取出一个或者少数几个关系模式R(O，A)，O为对象的键，如id等能唯一标识对象的属性列，A为该模式对应属性的得分，每个数据源都是按照属性A得分降序排列的。如果可以提取到m个这样的关系模式，我们可以假设多源数据的全部属性可以组成一个大的虚拟的关系模式R’(O，A1，A2，……，Am)，Ai分别对应属性i的得分。

每个节点都需要建立一个id索引，记为Li，其中i∈(1，m)，该id索引是按照相关属性的得分值降序排列的。索引Li的长度是可配置的。top-k查询的k值一般较小，所以为了减少维护索引的空间代价和处理开销，提高效率，设置了索引Li只有有限的记录。索引Li的长度可根据实际应用场景进行设置。

每个数据源节点都将把各自的索引Li发送给全局节点，全局节点将根据所有属性的索引建立全局的COIT。COIT包含了id以及在所在属性列的排名，表中每一行形式如下(id，rank inL1，rank inL2……rank inLm) 。对于每一条记录，它包括id和对象在所有节点的属性排名，表1是多源数据库索引一个实例，这一实例包括4列索引，各有5个元组，根据这一索引，按照COIT表构建方法，建立COIT表如表2所示。

表1　多源数据索引实例

表2　COIT表

1.2.1 建立COIT表的步骤

(1)多数据源节点获取按相关属性降序排列的id索引列Li，初始化COIT表，COIT表中每条记录形式如下(id，rank inL1，rank inL2……rank inLm)。

(2)逐行并行顺序访问m列id索引列，对读取到的索引列Li的id，若该id已经存在于COIT表中，则更新该id新读到的排名rank；若访问到的id不存在于COIT表中，则在COIT表末尾为该id新建一条记录，并将排名rank记录在相应的列。

(3)顺序访问COIT表，对没有排名信息的位置填入UNDEF，代表该id在该列的排名rank暂时没有读到。

1.2.2 建立COIT表的伪代码

算法1.建立COIT

Retrieve L1，L2，……,Lm

COIT[ ][ ] coit

Initialize coit

for i = 1 to the length of Li do

for j = 1 to m do

read current id

if (id is in coit)

//更新id在j个位置的排名为i；

updateCOIT(coit, id, j，i)

else

//在COIT表插入新id，并更新id

在j个位置的排名为i；

insertCOIT(coit, id, j，i)

end for

end for

fori = 1 to the length of COIT do

for j = 1 to m do

if (id rank is empty)

//更新id在j个位置的排名为UNDEF；

updateCOIT(coit, id,j，UNDEF)

end for

end for

return COIT

1.2.3 建立COIT表的流程图

COIT表的建立流程见图 1。

1.3 数据分割策略

算法处理的数据来自于不同源数据，每个数据源可能包含对象的一个或者少数几个属性信息，这些数据可以看做是根据不同属性垂直分布在不同节点的。top-k查询涉及到对象的多个属性的综合得分值，而这些属性数据一般来说分散在网络中的各个节点，如果直接查询，通信的代价将会非常高。

为了降低节点间通信代价，在查询处理之前，需要将这些不同源数据进行预处理和划分，使相同的对象划分到相同的分组。假设id是区分对象的标示符，则对象id被当做划分数据的标准；数据源被分割成的子数据组的个数与数据处理的并行度Pn一致。引言中介绍了本算法采用的MapReduce这一并行处理模型，Pn的值取决于MapReduce这一并行编程模型。源数据的元组被分割到哪个子数据组取决于数据分割方法，本算法采用了简单的hash函数映射的方法，将对象的id对N取模加1即得到子数据组的序号group.num，即

group.num=(object.id modN)+1。

(1)

图1　COIT表的建立流程图

这种分割函数简单方便，每个对象都能被映射到唯一的子数据组，而且由于对象的id一般是连续递增的，采用这种数据分割函数，能比较均匀的将数据分割到各个子数据组。不同源数据采用的数据分割函数要相同，在Pn和hash函数相同的条件下，可以保证不同源数据中id相同的对象被划分到子序号相同的子数据组。这样节点之间的通信量大幅度减少，以此来减少top-k查询时节点间的通信代价。

1.4 PCMRA算法

本节介绍算法PCMRA的原理，收到top-k查询之后，首先利用预先构建的COIT，得到候选id集合，然后根据数据映射规则，将分组的id集合发送到相应的节点，最后，由Hadoop平台计算输出整体的top-k查询结果。具体算法细节步骤如下：

(1)top-k查询解析。当接收到top-k查询时，首先根据查询请求进行解析，分析出查询所涉及的属性集合。

(2)获取COIT相关排名表列。根据解析后的属性集合，从COIT表中选取与这些属性相关的排名表列。

(3)排名表列化简。上一步已经获取所有id在查询属性列的所有排名，然而本文算法只关心这些属性的排名范围，即最大和最小排名，对于中间的排名可以不关心，因此可以对以上结果进行化简，只保留最大和最小排名。根据取到的相关的表列，逐行扫描，只保留每个id对象的最小排名和最大排名并分别定义为RankMin，RankMax。

(4)id集合排序。经过以上处理得到id及其排名范围，但是这些id可能是无序的，为了方便候选查询，需要对这些id对象进行排序。排序原则为，先根据RankMax升序排列，如果RankMax值相同，再按RankMin的升序排列。

(5)截止排名StopRank获取。为了获取候选id集合，需要事先获取截止排名，定义为StopRank。StopRank跟随k值的变化而变化的，根据查询的k值，顺序扫描排序后的id集合，当读到第k个id，得到该id的RankMax，表示当并行顺序访问到第RankMax行时，第一次至少有k个对象全部属性都已读到。该RankMax值即为StopRank。

(6)候选id集合获取。根据上述StopRank值，将所有RankMin不大于StopRank的id插入到候选id集合中。

(7)候选id集合分组。由于获得的候选id集合是混乱的，我们需要按照数据分割策略对它们进行分组和编号。数据是根据哈希函数来分割的，编号是按模取余来编号的。

(8)Hadoop并行计算和top-k结果输出。为了提高算法的并行度，启动Hadoop完成结果top-k计算。输入为分组并编号的原始数据和分组并编号的候选id集合。计算时，只需要根据原始数据的编号找到编号相同的候选id集合分组。只对包含在候选id集合的数据进行计算。被分配到做map操作的worker节点，做map操作“map(id， wi×listi.value)”，被分配到做reduce操作的worker节点，做reduce操作“reduce(id， list ( w1×list1.value, ……,wm×listm.value))”，最终输出最大的k个结果作为最终输出。

1.4.1 PCMRA算法伪代码

算法2. 获取候选id分组

AttrColumn[]related_Attributes

COIT[] [] coit

COIT[] [] coit1

COIT[] [2] coit2

ID[] Id

ID[N][] IdGroup

int i,j,RankMin, RankMax,StopRank

coit = Establish COIT( )

//解析top-k查询的相关属性；

related_Attributes= parse(String sql)

//获取COIT相关排名表列；

coit1 = retrieveCOIT(related_Attributes，coit)

for i = 1 to the length of coit1 do

for j=1 to the length of related_Attributes do

RankMin = read(coit1[i],1)

RankMax = read(coit1[i],1)

if (read(coit[i],j) > RankMax)

RankMax = read(coit1[i],j)

if(read(coit[i],j) < RankMax)

RankMin = read(coit1[i],j)

end for

insertCOIT(coit2, id, 1，RankMin)

updateCOIT(coit2, id, 2，RankMax)

end for

//排序，按RankMax升序排列，如过RankMax相同则按RankMin升序排列

sort(coit2)

//获取StopRank值；

StopRank = (coit2[k],2)

//候选Id集合获取

Id = retrieveIds(coit2, StopRank)

//候选Id集合分组

IdGroup = group(id,N)

return IdGroup

1.4.2 PCMRA算法流程图

本文PCMRA算法的流程见图2。

图2　PCMRA算法流程图

2理论分析

2.1 算法正确性证明

定理1对于任意一个k值和任意一个单调得分函数F，top-k结果集O是候选id集合X的子集。所有未出现在候选id集合X中的对象z，肯定不属于top-k结果集O。

证明假设用集合A表示所有的id集合，用X表示对于确定k值和确定得分函数F的候选id集合，用集合Y表示集合A中除去集合X剩下对象集合，即A-X。我们需要证明top-k结果集O是候选id集合X的子集，而显然候选id集合Y中对象个数是大于等于k的，因此不可能成为top-k结果集O的子集，因此只需要证明任何出现在集合Y中的对象z不属于top-k的结果集O。假设，F函数涉及到m个属性得分，而出现在集合Y中的对象z的m个属性得分为x1,…,xm。

根据候选id的获取方法，首先确定所有id的排名范围，即最大排名RankMax和最小排名RankMin，假设对m个排序列做并行顺序访问，id的最大排名RankMax和最小排名RankMin，分别表示该id第一次被访问的行数和最后一次被访问的行数，也就是当访问到第RankMax行时，该对象的所有属性得分都已经被访问到。然后对所有对象按照先按RankMax再按RankMin的升序排列，读取第k个id的最大排名RankMax即为StopRank，也就是表示当读到第StopRank行时，有k个对象的所有属性得分都已经被读到。最后取出所有最小排名RankMin小于StopRank的id放入候选id集合X，因为这些对象都曾经出现在StopRank行之前。

已知而每个排序列是按照属性得分的降序排列的，所以，显然先被访问到的得分要比后被访问的得分高。假设所有属性都被访问对象中，第k大的对象p的属性得分为x1,…,xm，显然对于任何i，都有xm≤xm，又因为得分函数F时单调增的，所以F(x1,…,xm)≤F(x1,…,xm,)，即对象集合Y中任意对象z得分肯定小于排名为k的对象得分，也就是说出现在集合Y中任何对象z都不属于top-k结果集O。

2.2 算法分析

本节根据算法流程进行详细的理论分析。COIT记录有P条记录，候选属性列有M个。

2.2.1时间复杂度按照算法详细流程，收到top-k查询处理之后对查询进行解析，得到k值和相关列，时间复杂度为O(1)；获取排名表列，进行化简，将所有id扫描一遍即可完成，算法时间复杂度为O(P)；对id集合排序，排序时只需要对MaxRank较小的前k个对象排序即可，遍历一遍所有id，时间复杂度为O(P)，前k个对象的排序，用插入排序法，时间复杂度为O(k2)；候选id集合获取和分组时间复杂度都为O(P)，上述步骤都在内存中可以完成，不需要I/O操作；最后Hadoop并行计算和top-k结果输出即可，时间复杂度跟Hadoop平台有关。除去Hadoop的计算时间，综上，时间复杂度为O(P+k2)。

2.2.2 空间复杂度算法预先建立的数据结构COIT只记录有限条记录，因此该空间开销是比较小的。整个算法中，Master节点需要维护一个全局的COIT表，假设有M个属性，对象id和M个属性都为整数，占4个字节，则COIT表每条记录占4(M+1)字节，整个COIT表占4(M+1)×P。在算法计算过程中，需要建立临时候选id集合，每个id只保留RankMax和RankMin，所以每条记录占12个字节，空间开销为12P字节。对id集合排序过程中，需要维护前k条记录，每条记录只保留id和RankMax，占8k字节。综上，空间开销为O(MP+k)。

3实验分析

在本节中，通过实验来评估算法PCMRA。首先，介绍实验设计。然后是具体实验以及结果分析。

3.1 实验设计

3.1.1 实验环境

实验在6台32位Linux机器上运行，每一台处理器型号为奔腾G620，主频2.60GHz的，内存4GB，硬盘8G,操作系统为centos。这些机器都预先安装并行数据处理引擎的Hadoop。这些机器与局域网连接起来，局域网网速为1000Mbps。算法用Java完成。

3.1.2 对比实验对比实验不采用预处理数据结构COIT，用Hadoop平台计算所有对象的得分，并排序得到前k个对象，本文称该对比算法为Naive算法。

3.1.3 数据集均匀分布数据集。

3.1.4 实验参数元组数N，一共分为10组，取值分别为1k，2k，3k，4k，5k，6k，7k，8k，9k，10k,默认取值为5k。

查询结果数k，也分为10组，取值分别为10，20，30，40，50，60，70，80，90，100，默认取值为50。

查询属性个数W，也分为10组，取值分别为1，2，3，4，5，6，7，8，9，10，默认取值为5。

3.1.5 性能指标运行时间time：显然算法运行时间越短代表算法的性能越好。

候选元组比率Ratio：Ratio为本文自定义的参数，它是总的元组数N、查询结果数K以及查询属性个数W的乘积与候选id个数Cn的比值的倒数的1000倍。容易看出，候选id个数Cn，随着总的元组数N,查询结果数K以及查询属性个数W的增加，其候选id个数显然是增加的，显然候选id个数Cn与以上3个因素是成正相关的。因此如果算法是线性可扩展的，则随着元组数N的线性增长，候选元组数也是线性增长的。倘若算法线性扩展能力好，在总的元组数N、查询结果数K以及查询属性个数W其中2个值固定，一个值线性增长的情况下，候选元组比率应该Ratio是一常量，甚至是降低的。Ratio的计算公式如下：

(2)

3.1.6 查询设定为了方便起见，查询请求的各属性权重设为wi=1/W,查询属性列选取COIT表中前W列属性。

3.2 实验及结果分析

3.2.1 实验一：元组数N的影响设定k=50，W=5，实验一反映了PCMRA和Naive算法随着元组数N的变化，算法的性能指标的变化。图3(a)表明随着元组数从1k增加到10k，PCMRA算法候选元组比率Ratio从0.17左右降到大约0.03，并且在元组数为10k时，候选元组比率Ratio仅为0.03，根据公式计算，候选元组数Cn仅为总元组数的8%左右，筛选的不相关元组数能达到90%以上，并且由图中趋势推断，随着元组数的增加，候选元组比例仍在降低，而Naive算法一直稳定在4。Ratio越低说明算法性能越好，说明PCMRA算法性能更优，明显具有更好的扩展性。图3(b)表明随着元组数从1k递增到10k，PCMRA算法运行时间从24s增到27s，时间增加12.5%，而Naive算法从25s增加到34s，时间增加36%，显然Naive算法比PCMRA算法运行时间慢，并且增幅比为后者的将近3倍。由图中趋势看随着元组数N的增加，这一差异将更加明显，显然PCMRA算法在时间性能上更好。

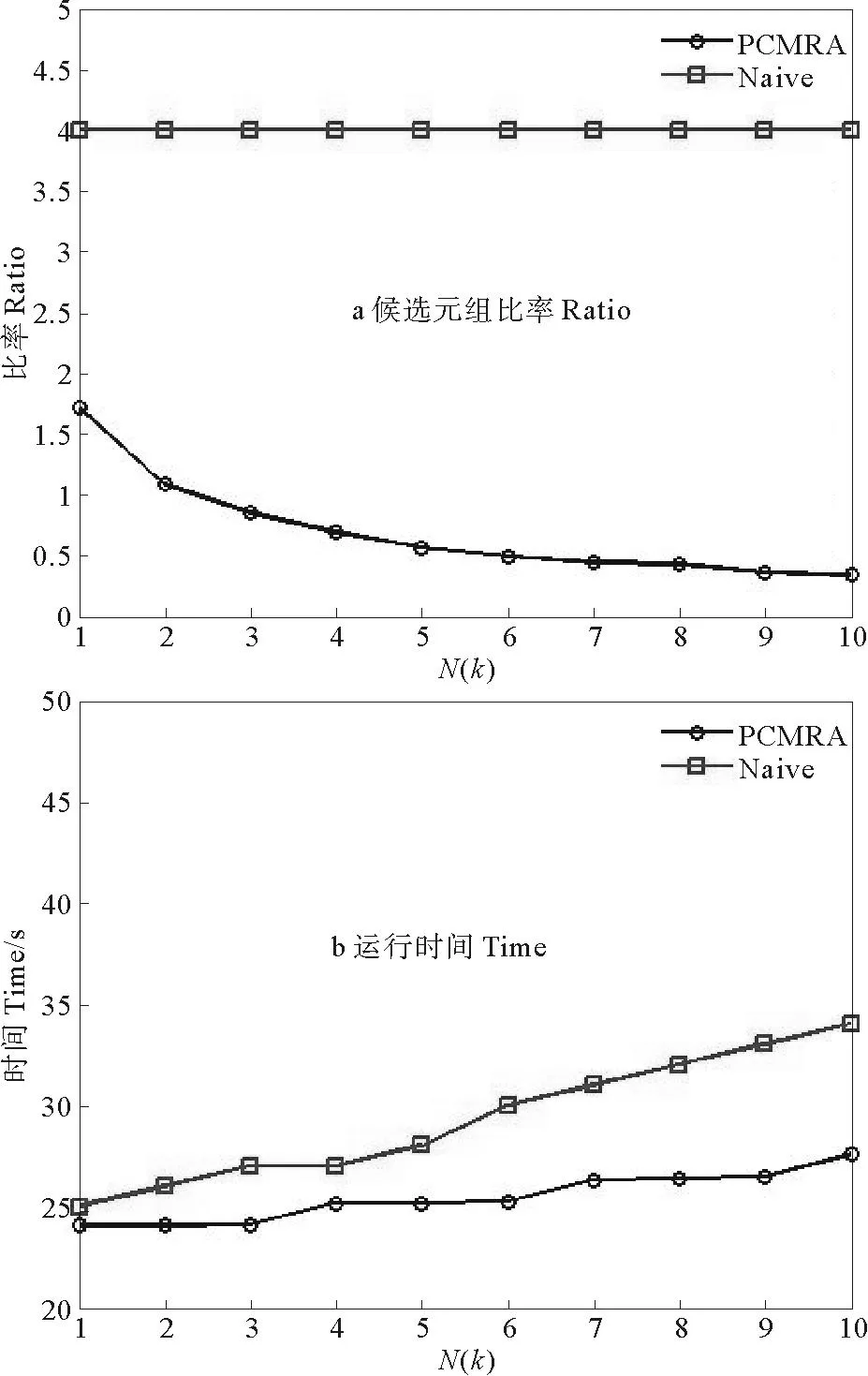
图3　元组数N的影响

3.2.2 实验二：查询结果数k的影响设定N=5k，W=5，实验二反映了PCMRA和Naive算法随着查询结果数k的变化，算法的性能指标的变化。图4(a)表明随着查询结果数从10逐渐增加到100，PCMRA算法候选元组比率Ratio从0.85降到0.45左右，虽然Naive算法候选元组比率Ratio从20降到2，降幅明显，但是前者一直比后者低，并且前者比例也一直在降低。同实验一分析结果一致。图4(b)表明随着查询结果数从10递增到100，PCMRA算法运行时间从24s增到25s，而Naive算法从25s增加到28s，2个算法时间增加都不明显，但是PCMRA算法仍然比Naive算法运行时间短，PCMRA算法在时间性能上仍然优于Naive算法。

图4　查询结果数k的影响

3.2.3 实验三：查询属性个数W的影响设定k=50，N=5k，实验三反映了PCMRA和Naive算法随着查询属性个数W的变化，算法的性能指标的变化。图5(a)表明查询属性从1个增加到10个，PCMRA算法候选元组比率Ratio比例一直在0.5左右，仍有不太明显的降低趋势，同实验二，Naive算法降幅明显，但是仍然一直比PCMRA算法Ratio要高的多，因此分析结果同实验一一致。图5(b)表明查询属性从1个增加到10个，PCMRA算法运行时间从23s增到25s，而Naive算法从25s增加到30s，同实验二2个算法时间增加都不明显，但是PCMRA算法仍然比Naive算法运行时间短，PCMRA算法在时间性能上仍然优于Naive算法。

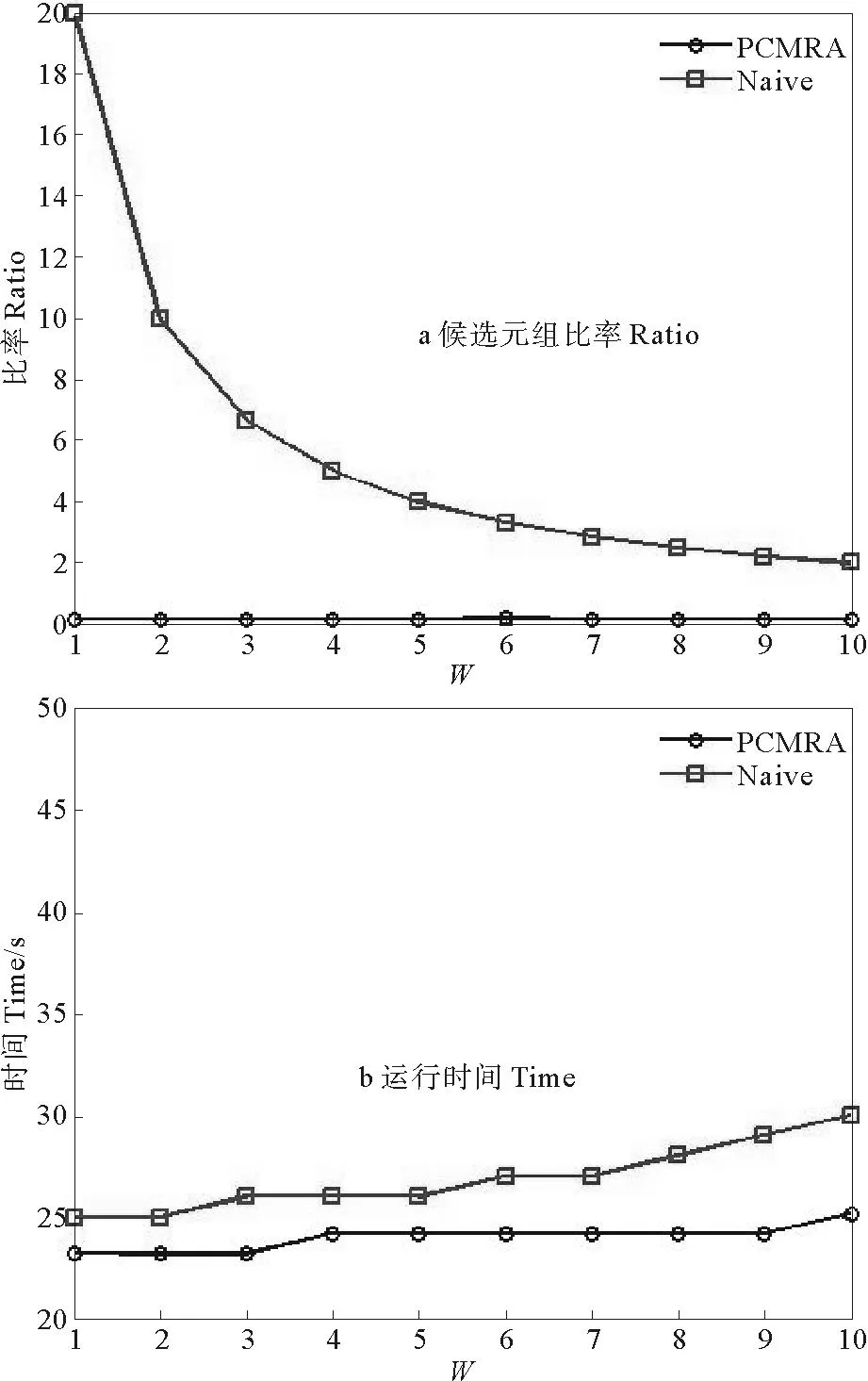
图5　查询属性个数W的影响

4结语

本文中，我们分析了当今数据的发展趋势，而现有算法比较耗时，并需要大量的通信。随着网络数据的增加，传统的top-k算法更加难以处理这些问题。所以本文提出了一种分布式环境下top-k算法PCMRA。它仅需要较小的构建代价和较少的空间开销，就可以建立数据预处理结构COIT。借助COIT，使用我们的数据分割策略，并采用并行编程模型MapReduce，我们的算法PCMRA只需要与服务器的一轮通信就可以完成top-k查询。本文给出了算法正确性证明，并对算法的时间复杂度和空间复杂度进行分析。实验部分表明该算法仅涉及有效通信，并且运行时间短，查询结果准确，可扩展性好。这表明该算法在一定条件下优于现有的算法。

本文算法设计针对大数据的应用环境的确定数据库，但是随着数据的爆炸增长，数据的不确定性为top-k查询问题带来了很多困难，围绕不确定型数据模型和可能世界语义的top-k查询已经引起了广泛的关注。但可能世界语义的top-k查询问题仍需要大量的研究。下一步，我们将本文的算法扩展到不确定数据库。首先定义基于多属性综合得分的可能世界语义的top-k查询模型，然后针对此查询，设计一种带有预处理结构的不确定数据库上top-k查询,并沿用数据分割和采用MapReduce并行编程的思路。

参考文献：

[1]Lohr S. The Age of Big Data[J]. SR1, online: http: //www.nytimes.com/2012/02/12/sunday-review/big-datas-impact- in-the-world.html, 2012, 16(4): 10-15.

[2]Han X, Li J, Wang J, et al. TJJE: An efficient algorithm for top-k join on massive data[J]. Information Sciences An International Journal, 2013, 222(3): 362-383.

[3]Ronald Fagin, Amnon Lotem, Moni Naor. Optimal aggregation algorithms for middleware[J]. Journal of Computer and System Sciences， 2003: 102-113.

[4]Zhao K, Tao Y, Zhou S. Efficient top- k processing in large-scaled distributed environments[J]. Data & Knowledge Engineering, 2007, 63(2): 315-335.

[5]Cao Pei, Wang Zhe. Efficient Top-K Query Calculation in Distributed Networks[C].Newfoundland: PODC, 2004: 206-215.

[6]Michel S, Triantafillou P, Weikum G. KLEE: A Framework for Distributed Top-K Query Algorithms[J]. Vldb, 2005: 637-648.

[7]Chrysakis I, Chalkidis C, Plexousakis D. A Detailed Evaluation of Threshold Algorithms for Answering Top-k queries in Peer-to-Peer Networks[J]. 2010.

[8]Dean J, Ghemawat S. MapReduce: Simplified Data Processing on Large Clusters.[J]. In Proceedings of Operating Systems Design and Implementation 2004, 51(1): 107-113.

[9]Soliman M A, Ilyas I F, Chen-Chuan Chang K. Top-k Query Processing in Uncertain Databases[C]//Data Engineering, 2007. ICDE 2007. IEEE 23rd International Conference on. IEEE, 2007: 896-905.

[10]Hua M, Pei J, Zhang W, et al. Ranking Queries on Uncertain Data: A Probabilistic Threshold Approach[C]. Florida: Computer Science Department, Florida State University, 2008: 673-686.

[11]Yi K, Li F, Kollios G, et al. Efficient processing of top-k queries in uncertain databases with x-relations.[J]. IEEE Transactions on Knowledge & Data Engineering, 2008, 20(12): 1669-1682.

[12]Cormode G, Li F, Yi K. Semantics of Ranking Queries for Probabilistic Data and Expected Ranks[C].Chicago: 2014 IEEE 30th International Conference on Data Engineering, 2009: 305-316.

责任编辑陈呈超

PCMRA: An Efficient Top-kAlgorithm in Distributed Environment

WANG Ning, QU Hai-Peng, FAN Ling

(College of Information Science and Engineering, Ocean University of China, Qingdao 266100, China)

Abstract：With the unceasing expansion size of the data and the increasing complexity of data types, human race has entered the era of big data. On the one hand, there is a sharp increase of the data provided from different areas and applications, on the other hand, the traditional data processing techniques can not cope with such a large-scale data, thus this situation brings serious challenges to the current data processing techniques. We are on a pressing demand to effectively dig out the beneficial information we need, thus we have to raise a faster and more effective query technique. Ranking queries, which is known as top-k query, is one of various complex data queries. It works by calculating the scores of all objects by an aggregation function, and then return the top-k objects with the highest scores. For many interactive systems, efficient Top-k query are very important. Top-k query problem also involves a lot of database processing technologies, including indexing and query optimization, etc. Top-k query is now attracting more and more attention for the broad use and the efficiency, so it is now a hot spot in research area, and it is also has very important theory value and the very extensive application prospects. This paper mainly researched on the corresponding top-k query algorithm for large-scale data, and then made some innovation. Finding the top-k best records among the potentially huge answer space in real time for many interactive systems, is a challenging issue today, for there is an increasing trend that more and more data needs to be processed. With the increase of network traffic, these problems will become unsolvable. Learning from the good features of the traditional top-k query processing technology and using parallel programming model - MapReduce, this paper proposes a novel top-k algorithm PCMRA(Data Partitioning and COIT Indexing Top-k query Algorithm based on MapReduce). Our solution develops a pre-construction algorithm to construct COIT (Candidate Objects Index Table), adopting a new strategy of data partitioning, completing the top-k query in one round by means of parallel programming model: MapReduce. The correctness proof and cost analysis of PCMRA are present in this paper. Experiments show that the algorithm only requires lower construction cost and less space overhead . A small number of candidate objects can be selected in a relatively short period of time, greatly saving computing and communication resources, and also the algorithm has good scalability.

Key words:top-k query; COIT; data partitionin; MapReduce; massive data

DOI：10.16441/j.cnki.hdxb.20140032

中图法分类号：TP311

文献标志码：A

文章编号：1672-5174(2016)02-138-08

作者简介：王宁(1987-)，女，硕士生。E-mail：wangnynn@gmail.com❋❋通讯作者： E-mail:quhaipeng@ouc.edu.cn

收稿日期：2014-03-05；

修订日期：2014-10-09

基金项目：❋ 国家自然科学基金项目(60773057)；国家海洋局海洋公益项目(201105033)

引用格式：王宁， 曲海鹏， 范令. 一种分布式环境下高效查询算法[J]. 中国海洋大学学报(自然科学版)， 2016, 46(2)： 138-145.

Supported by National Natural Science Foundation of China(60773057)；The State Oceanic Administration of Marine Public Welfare Projects(201105033)