课堂,由“学”而“生”
2016-03-23刘耀兵
刘耀兵
[摘 要]课堂是学生学习的主阵地,教师只有将“讲堂”转变为“学堂”,教学才会发生质的变化。这样的学习带来的不是表面的繁荣,而是学生生命的自觉回归、自主学习、自由管理、自然生长。
[关键词]课堂 学堂 自主构建 自我展示 自由提问 自然点拨
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2016)08-025
朱永新教授认为:“如果课堂不能给学生以智慧的挑战、情感的共鸣、发现的愉悦,而只是让他们成为一个容器消极地接受、被动地应付,学生一定不会享受幸福、完整的教育生活。”同时,卢志文先生在《今天我们怎么做教育》一书中指出:“理想课堂应该是学堂,而不是讲堂。理想课堂要以学习为中心,一切从孩子出发,突出他们的主体地位,而不是旁若无人的自弹自唱……”课堂教学的目的旨在让学生获得发展,使学生因自主学习而自我驱动,因展示活动而获得尊严,因自由提问而缩小差距,因适时点拨而深入探究。
下面,笔者以苏教版小学数学五年级“平面图形的面积计算复习”一课教学为例,浅谈自己的一些实践与思考。
一、自主建构,让学生成为学习的主人
教学片断:
师:我们已经学习了长方形、正方形、平行四边形、三角形和梯形的面积计算,这节课就对这些知识进行整理。请同学们拿出自主整理单(如下),把有关内容填写在空白处。
平面图形的面积整理单
姓名:
我们已经学过了长方形、正方形、平行四边形、三角形、梯形的面积计算,请把它们有条理地整理出来。(提示:可以列表整理、画图整理等)
师:下面进行小组交流,注意交流的要求:(1)由每组的3号和4号同学先说,有缺漏的地方其他组员及时补充;(2)比比谁整理的清楚、完整。
……
建构主义认为:“知识结构转化成学生的认知结构,是学生主体通过顺应和同化的方式实现的,是学生思维活动内化的结果。”上述教学片断中,教师给学生提供充分从事数学活动的机会,并放手让学生自主梳理所学的知识。学生依据自己的理解和掌握的知识,创造出不同的整理图,每个图都是学生原有认知重新构建的结果,富有个性化色彩。在此基础上发挥小组的力量,让学生相互学习、相互促进、相互提高,在学习小组内交流自己梳理建构的成果。这样既使学生获得成功的体验,又使他们相互借鉴、取长补短,还让学生学习到更多的梳理知识的方法,为以后的复习整理打下基础。由此,在相互启发下,整个单元的知识结构和思想方法体系完整地展现在学生面前,打破了传统教学单线性输出的弊端,呈现出多样化的表达方式。尤为重要的是,学生在自主梳理中不断学会建构知识的方法。
二、自我展示,让学生获得学习的尊严
教学片断:
师:已经完成任务的小组上台展示你们的整理成果。
生1(出示下图):我是用列表法进行整理的。
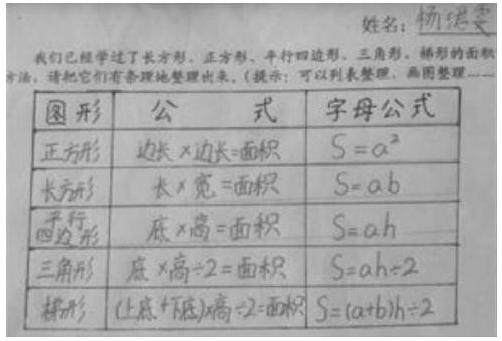
生2(出示下图):我用的是“苹果整理法”。
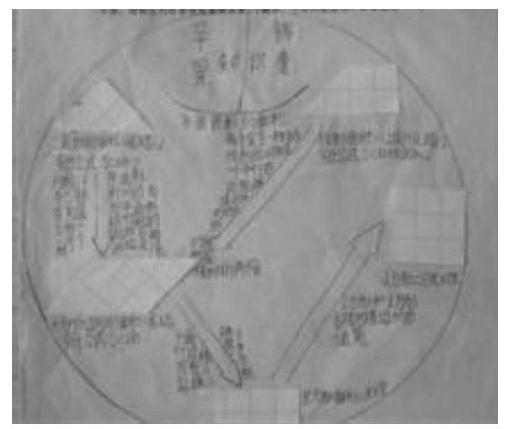
生3(出示下图):我根据知识之间的关系画了一幅示意图。
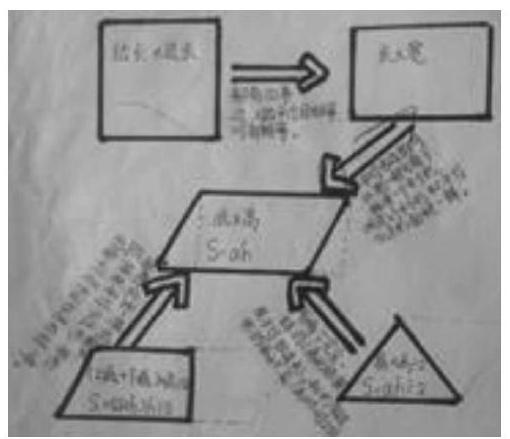
生4:我对你的方法进行补充。三角形还可以用剪拼的方法,推导出它的面积计算方法(如下图)。
生5:我对生3的图提一个建议。我们是把平行四边形通过剪、移、拼等方法转化为长方形的,所以应该把箭头的方向对换一下。
师:同学们都整理得非常好,不仅整理出了各种平面图形面积的计算方法,而且把知识的来龙去脉和相互之间的联系表达得清清楚楚,让人一目了然。
……
本环节的展示活动为学生提供了展示自我、获得尊严、发展能力的机会,促使他们拿出看家本领,使出浑身解数去讲解、演示、表演、合作。同时,展示机会的获得是平等的,台下学生随时可以打断发言者进行质疑和补充,也可以上台辩论和反驳。这样,无论是一知半解者的只言片语,还是融会贯通者的洋洋洒洒;无论是能言善辩者的吹毛求疵,还是学习有成者的明知故问,课堂呈现出一派盎然生机。这里,教师要做的就是让学生勇敢地站起来,尊严地坐下去,然后静观其变,静待花开。
展示活动改变的是学生和学习的关系,使学生从被动接受变为主动获取,将知识学习由枯燥变得有趣。当学生为尊严而付出时,就获得了自我价值的实现,于是一次次小的成功就让他们树立了自信心。当一个人建立了自信,即使遇到失败,也会在哪里跌倒就从哪里爬起来,在经历了失败和成功的轮番洗礼后,自信就渐渐被自强代替。
三、自由提问,让学习变成学生的需要
教学片断:
师:经过刚才的整理和交流,你又想到了哪些新的问题?
生1:平行四边形、三角形和梯形的面积推导过程有什么相同之处?
生2:为什么梯形和三角形的面积计算要除以2?
生3:为什么要先学习长方形的面积?
生4:如遇上圆等特殊图形时,要如何算出面积?
……
师:同学们提的问题都很有价值,看得出你们对平面图形面积的认识又加深了一步。下面,以小组为单位,讨论一下这些问题该如何解答。
生5:我来回答第一个问题。我们在学习平行四边形、三角形、梯形的面积时,都是先把新的图形转化成已经学过的、会计算的图形,再推导出它的面积计算公式。
师:把未知转化为已知。
生6:我来回答第二个问题。因为我们是把两个完全一样的三角形或梯形拼成一个平行四边形,而每个三角形或梯形的面积只是这个拼成的平行四边形面积的一半,所以要除以2。
生7:我来回答第三个问题。因为长方形的面积公式是推导其他图形面积公式的基础,即先由长方形面积公式推导出正方形、平行四边形的面积公式,再由平行四边形面积公式推导出三角形、梯形的面积公式,所以要先学习长方形的面积公式。
……
亚里士多德曾说过:“思维是从疑问和惊奇开始的。”学生头脑中只有存在问题,才会去思考,才会有求知的愿望和要求,才会主动学习知识,这样知识的获取对于他而言才是有意义的。当学生有能力提出自己的问题时,就成为学习的主人,因为“只有自己的问题才是自己的思考”。
维果斯基也说过:“当个体遇到新的和感到困惑的情景而努力去解决由这种经历引发的认知冲突时,他的智力就会得到发展。”同时,他认为,儿童在为了解新知识而进行质疑的过程中,就把新获得的知识与先前学习的知识联系起来,并赋予了新的意义。这里的“感到困惑”,说的就是发现问题、提出问题。因此,课堂教学中,教师应让学生体验到头脑中装着问题,学习就有了内在的动力,原本枯燥、抽象的被动学习就会转变成问题的探索和解决的过程,明白这是一个接受挑战并且可以带来成功感的过程。
四、自然点拨,让学生的学习变得更加厚实
教学片断:
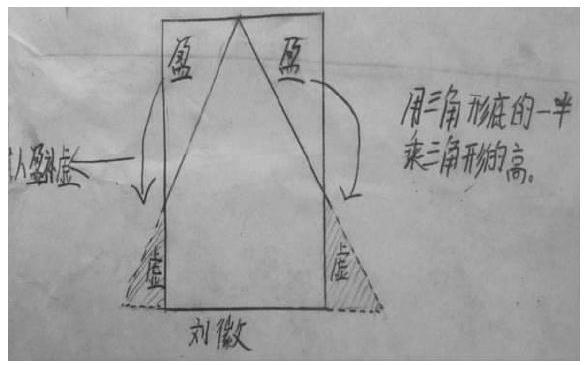
师:看来,长方形是基础,要先学。可梯形不服气了:“凭什么最后学我?”难道梯形的面积计算就真的没有别的作用吗?下面,让我们进入“图形变变变”环节。
师(出示右图):求图形的面积,只列式不计算。
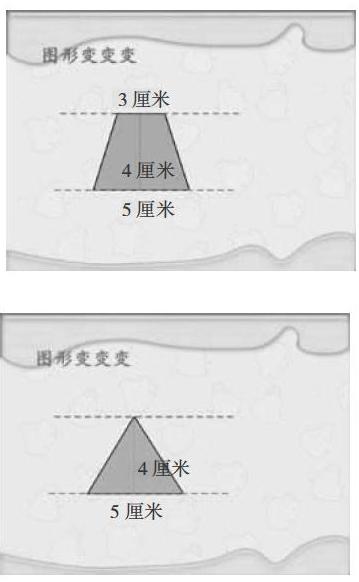
生1:这是个梯形,面积是(3+5)×4÷2。
师:对。现在把上底渐渐缩短(如右图),变成了——
生2:变成了一个三角形,面积是5×4÷2。
师:是的,当梯形的上底渐渐变短,等于0时,就变成了三角形。现在,你还能用梯形的面积公式计算吗?
生3:不能。
生4:行的。可以把上底看作0,用(0+5)×4÷2来计算,经过变化,也能得到5×4÷2,从而算出三角形的面积。
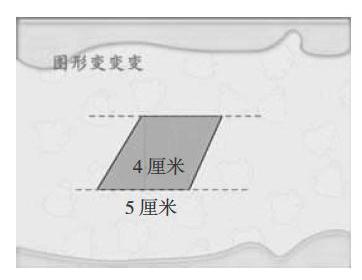
师:不错。看来,梯形的面积计算还能解决三角形面积的问题。如果把图形变化(如右图),上底渐渐变长,再变长,当和下底一样时,就变成了——
生5:就变成平行四边形,面积是5×4。
师:上底从0延长到5,就变成了平行四边形,还能用梯形的面积公式计算吗?
生6:可以。这时可以把它想象成一个特殊的梯形,它的上底是5厘米,下底也是5厘米,高是4厘米,用(5+5)×4÷2计算,化简后就是5×4。
师:解释得太好了。现在大家有什么想法?
生7:看不出小小的梯形面积计算公式竟然有这么大的作用,对三角形、平行四边形的面积都可以算。
生8:图形之间的联系真奇妙!三角形其实就是上底为0的梯形,平行四边形就是上底和下底相等的梯形,真是太好玩了。
生9:我现在理解了为什么最后学梯形的面积计算了,因为它能涵盖前面所有的面积计算方法。
师:是啊!图形世界就是这么奇妙,它们之间有着千丝万缕的联系,还有更多的奥秘等着我们去探索。
师:还剩最后一个问题:如果遇到圆形,我们该如何计算它的面积?大家用今天的学习经验想想办法。
生10:我觉得也可以把它转化成学过的平面图形。
师:把未知转化为已知是一种非常有效的学习方法。那么,凭你的感觉,可以把圆转化成什么图形呢?
生11:可以转化成长方形、三角形或梯形。
师:这些猜想是否可行呢?有兴趣的同学可以课后研究一下。
……
学生由于受年龄特点、知识结构及教材、目标、手段等多方面的影响,不可避免地会出现思维障碍。这时教师要及时地诱导和启发学生产生解决问题的欲望,将思维导向深处,促使学生产生顿悟,越过障碍,激活思维。“要使学生从不知到知,从知之不多到知之甚多,重要的不是讲述,而是点拨。”课堂上教师适时、适度、适当的点拨,可以帮助学生化难为易、变困惑为顿悟,促进学生的思维发展,提高学生的学习能力。同时,教师的点拨还可以把学生学习的触角引向课外更为广阔的时空。如上述教学中,教师也许只是点到即止,却让学生对“学”欲罢不能,其深层意义在于激发和保护了学生的好奇、惊异之心,引领他们无限可能地生长。
张奠宙教授认为:“在好奇心的驱使下,我们才能取得数学的创新和突破。”理想的数学课堂,其应有之义就是培养学生对数学怀有好奇、惊异之心,以一种强烈的愿望去认识和理解数学。也许,学生的学习并不是从上课铃响才开始的,下课铃响只能代表课堂、学校学习的结束,并不代表学生学习的结束,而这恰恰宣布了另一种更大范围、更大意义的学习悄然开始。
“教育者站在孩子身边,为他们好学而设计——主要依靠他们自己的学,最大限度依托上天所赐给他们的禀赋,来为他们服务。”课堂是学生学习的主阵地,是校园生活中最有意义、最有价值的部分。我们只有将“讲堂”转变为“学堂”,教学才会发生质的变化,这样的学习带来的不是表面的繁荣,而是学生生命的自觉回归、自主学习、自由管理、自然生长。
课堂,由“学”而“生”!
(责编 杜 华)
