发展学生数学学习能力：案例与反思

江喻洪

摘 要：数学课程标准（2011年版）指出，通过数学学习学生要获得数学的基础知识、基本技能、基本思想、基本活动经验，要增强学生发现和提出问题的能力、分析和解决问题的能力。这无疑是为学生数学学习能力的发展指明了方向。以《2、5的倍数特征》一课为例，思考如何发展学生的数学学习能力。

关键词：数学；学习能力

发展学生数学学习能力是数学课堂教学的根本宗旨。下面，结合小学数学五年级《2、5的倍数特征》这一课例，谈谈自己的思考与实践。

案例描述

一、复习旧知，引入新课

（一）引入：同学们，前面我们学习了倍数和因数的知识。要判断一个数是不是另一个数的倍数，你会吗？

（二）判断：17是5的倍数吗？ 24和3呢？ 325和7呢？

师：这组数据有点大（325和7），不能很快判断出来，怎么办？

小结：看来，用除法计算可以判断一个数是不是另一个数的倍数。但是当数据比较大时，比较麻烦。其实，有些数的倍数是有一定特征的，我们可以根据它的特征不用计算就可以很快判断一个数是不是它的倍数。今天这节课，我们就先来研究最简单的2、5的倍数特征。（板书课题：2、5的倍数特征）

二、主动探索，寻找特征

（一）探究2的特征——明确探究方法

1.明确方向，达成共识

（1）要想研究2的倍数特征，你觉得首先应该先干什么？（要列举出一些2的倍数）

（2）列举出一些2的倍数来干什么？（列举出来方便进行观察，找出特征）

（3）大家都同意这个意见？看来同学们达成了共识：要先列举出一些2的倍数来，（板书：列举）再来观察分析有什么特征。（板书：观察）

2.动手操作，观察分析

先列举出一些2的倍数，然后进行观察分析，把你的发现写下来。

3.展示交流，强化对比

（1）有序而适度列举：先看这位同学列举的，我们采访他一下，这些数据你是怎样得到的？（用2乘1、2、3、4……）省略号是什么意思？（2的倍数无限个）。

（2）无序列举：我们再来看看这位同学列举的，你觉得哪个好一些？为什么好？

（3）有序但数据比较多：我们再来看看这位同学列举的，你有什么想说的？

小结：看来在列举数据时我们不但要做到有序，还要注意适度，边列举边观察，只要能观察出来基本特征就不用再列举了。如果还能做到这样有规律地排列就更好了，这样更便于观察分析（课件）。

4.发现共性，提出猜想

通过列举和观察，发现了2的倍数有什么共同特征呢？你们刚才观察出来的特征只是针对列举出的一部分数据得出的。这只能算是你们的一个猜想（板书：猜想）。对于更大的2的倍数是不是也有这样的特征呢？怎么办？

5.举例验证，检验猜想

你的建议很好，举几个满足特征的例子用除法来验证一下。（板书：验证）学生举例验证。（注意正反两面举例）

小结：刚才通过大家从正反两个方面举例验证，现在我们可以坚信前面的猜想是正确的：2的倍数特征就是个位上是0、2、4、6、8。

练习：判断下面哪些数是2的倍数？（略）

（二）探究5的特征——运用探究方法

师：同学们真能干，运用列举、观察、猜想、验证这四个步骤自己探索出了2的倍数特征。那5的倍数特征又是什么呢？相信大家能运用这个方法探索出5的倍数特征。

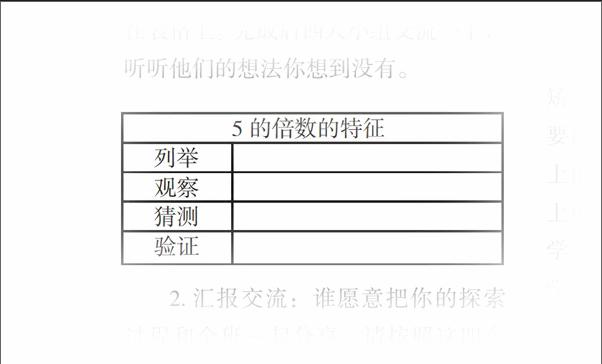
1.自主运用方法：为了方便交流，请你把探索过程的四个步骤完整地写在表格上。完成后四人小组交流一下，听听他们的想法你想到没有。

2.汇报交流：谁愿意把你的探索过程和全班一起分享。请按照这四个步骤说说你是怎么发现5的倍数特征的？（引导学生表述：我列举了5的倍数……观察发现末尾……于是我猜测5的倍数……然后我举例……来验证，说明猜测是正确的）

3.达成共识：同学们说的真不错，老师把你们这个重要发现写在黑板上。（板书：5的倍数特征的确是个位上是0或5）

练习：下面哪些数含有因数5？（略）

（三）认识奇数和偶数（略）

三、课堂练习，巩固知识（略）

四、全课总结，反思评价（略）

五、拓展延伸，引发质疑（略）

案例反思

一、价值取向的角度——找准学生能力发展的生发点

面对一堂数学课的教学时，首先需要思考，我的价值取向是什么？我希望这堂数学课给学生带来什么样的变化？是数学知识的掌握，还是数学方法的渗透？是数学现象的呈现，还是数学本质的把握？是数学思考的深化？还是数学交流的升华？这才是从价值取向的角度思考问题，也就是 “教什么”的问题。

学生学习能力的发展体现在很多方面，比如，我们对某一知识点或某一习题的深度剖析、变式练习、对比矫正，这些是能力发展，而且是很重要的能力发展。但我认为这是“点”上的能力发展，更重要的是在“线”上的能力发展，也就是具体每节课的学习过程中的能力发展。它受整个教学过程中教材组织方式、学习方式、教学关注点等众多因素的影响。因此因人而异，千差万别。

有了价值取向的有意识思维，就需要在教学过程中找到学生能力发展的生发点。

《2、5的倍数》一课，能力发展的生长点又在哪里呢？教材中有找一找100以内2的倍数的数表，旨在通过找出2的倍数来分析其特征。这是否有抽样的思想。但问题是，我们在解决问题时，谁来给我们这些脚手架？没有。这个数表是否涉及为什么要列举？列举来干什么？怎么列举？怎样排列？这一系列问题是否就是数学素养的问题？有数学思想，有数学方法，它较之本节课基本数学知识而言是否更有价值。它是否可以作为本节课的生发点，并以此为主线来设计和组织教学呢？

二、学习方式的角度——找到能力发展的现实载体

有了这样的思维，找到了这样一个生发点，就必须选择一种适合于达成这个生发点的组织形式或学习方式，即“怎么教”的问题。所以探究式学习就成为实现这一目标的方式。

在探究过程中，教师充分引导学生探究时为什么列举？列举的目的是什么？列举中排列的学问（教学过程中教师专门设计一环节对比学生列举的数据及排列的方式，并介绍怎么排列更有利于观察数据的特点）等实质问题，这些都影响着学生数学思维的习惯，渗透了探究数学问题的基本思考方法。这是本课的一大亮点。

在5的特征的学习中，看似教师没做任何工作，其实做了两个非常重要的工作。一是要求学生按照前面的四步独立探究5的倍数的特征。二是要求学生按照四步进行具体探究过程的交流，这是本课的第二大亮点。

本课打破教材的编排，并不是在学习了2的倍数的特征后就立即进行相关知识点的学习及处理。如奇数、偶数及其无限性，自然数的分类等。而是直接运用这一方法进入5的倍数特征的自主探究。之后，才在练习中通过习题的方式呈现其他知识点，较好地保证了运用2的倍数特征的探究方法去自主探究5的倍数特征的方法衔接。这是本节课的第三大亮点。

正因为有了探究的学习方式，才较好地达成了“数学思想和方法的学习”这一正确价值取向的实现。

作者单位：重庆市江北区两江国际小学鱼嘴实验学校