引水渠道单井注水对不冻长度的影响
2016-03-23赵梦蕾刘贞姬宗全利
赵梦蕾,刘贞姬,宗全利
(石河子大学水利建筑工程学院,新疆 石河子 832000)
新疆位于我们中国西北边陲的严寒地区,每年冬季气温极低,一些河流水温便急剧下降,导致各种不同程度的冰情产生[1],它们不仅对渠道输水能力有影响,也带来了一系列影响工农业生产、人民生活及水电站经济效益等问题。为了有效地改善渠水水温,我们利用抽水融冰的技术,即用水泵抽取温度较高的井水,将其注入水温较低的引水渠道内,使它们在渠道中混合后进行热交换,从而提高渠道水温,保证引水渠道冬季运行畅通。
国内外对河流的水温变化、水内冰演变及体积分数的分布等已有大量研究,并对不冻长度的计算总结出一些经验公式。其中李克锋等结合某流域水温原型观测资料,通过分析水温与气温、太阳辐射、湿度和风速之间的相关关系,采用最小二乘法建立了水温与气温、湿度和风速三者之间的多变量函数方程式,提出了一种利用气象因子估算天然河道水温的新公式[2];在一维模型的基础上,吴剑疆等又建立了河道中水内冰形成及演变的垂向二维紊流数学模型,确定水内冰体积分数沿水深呈指数分布[3];王晓玲等建立了三维非稳态Euler-Euler两相流k-ε紊流模型,通过模型模拟分析了气温变化条件下流速、水温、冰温及冰体积分数的沿程分布[4];Shen等采用二维河冰模型,模拟了Shokotsu河冰塞形成过程[5];Wadia和Betchelor运用一维方程对水内冰质量及热力交换进行了研究[6,7];邓朝彬等对香加水电站引水渠冬季注水升温运行进行了简单的介绍,也得出了相应的经验公式计算不冻长度[8];靳国厚等预测了冰塞发生的可能性并预测了其发生的位置[9];王峰等结合新疆红山嘴电厂技术方案,给出了电厂井口布设的经验公式[10];王文学等在金沟河电站以升温运行原型观测资料为基础,结合冬季渠道水温散失的物理过程,推出了一个计算不冻长度的公式[11]。
以上这些研究表明,对于寒区引水工程来说,气温、地温、太阳辐射、风速等太多因素都会影响水温变化。现有研究主要集中在水流中冰的形成和演变过程上,目前从水力条件、热力条件和气候条件等分析水渠不冻长度现有研究成果对此也鲜有涉及。因此本文在对引水渠道单井注水后对不冻长度的影响进行了分析研究。
1 试验概况
1.1 试验模型
试验以新疆红山嘴水电站中引水渠道为原型,结合试验地条件稍作修改,按照重力相似准则设计水槽试验模型,设计比尺为1∶20。试验场地占地面积8.5 m×22 m,模型水渠总长度为77 m,共设计3个弯道,纵坡为1∶1 000。该水槽试验在石河子大学水利建筑工程学院水工试验室外大厅进行,室外大厅冬季温度只要低于0 ℃就可以进行试验,而新疆石河子市每年冬季温度低于-10 ℃均超过100 d,所以融冰水槽试验完全可行。设计的水槽模型结构如图1所示。

图1 试验模型示意图Fig.1 Sketch of the experiment
图1中蓄水池为引水渠提供冷水水源,引水渠分弯道段和直线段,弯道段足够长确保引水渠内形成冰花,直线段为融冰试验段;变频装置能够保证连续稳定地提供压力水源,并能根据需要调节不同的流量档次;融冰水源采用室内自来水,并用加热棒和冰块来提高和降低水源温度,以获得不同温度融冰水源。
1.2 试验安排
试验分别在不同水力、热力、气候条件下进行,并根据水流状况设定测量断面,在每个断面处用电子流速仪测量流速,每个断面测量5次,以5次平均值作为该点的平均流速[12]。同时,每个断面处用水桶取样,运用称重法计算该处冰花密度,每个断面测量3次,以3次平均值作为该点的平均冰花密度。整个试验观测过程中气温测量结果为最高气温为-9 ℃,最低气温为-27 ℃,完全低于水的冰点温度。试验流量根据红山嘴原型试验数据,按照重力相似准则,模型与原型之间的流量比尺为1∶400,根据原型中井水与渠水流量大小,分别选取模型渠水流量为0.5、0.75和1.0 L/s,模型井水流量为0.06、0.12、0.18 L/s,加水点则选取在模型渠道里程的32 m处,如表1所示。

表1 试验组次安排 L/s
2 试验数据分析
2.1 水力条件不冻长度的影响规律
2.1.1渠水流量对不冻长度的影响规律
在井水流量、流速以及水温等因素保持不变,只改变渠水流量,研究其对不冻长度的影响。通过室外的蓄水池对水温进行降温,将渠水流量分别为0.5、0.75和1.0 L/s的冷水引入引水渠,在32 m处注入0.06 L/s的井水,5 min后对各断面进行数据采集、称重和计算,得出该工况下冰花密度的变化规律。随后当水温降至初次测量的水温时,注入0.12 L/s的井水,重复上述步骤,直至将注入0.18 L/s的井水后的数据全部测量记录完,试验结束。该试验进行时间为3 d,试验过程中气候温度最高-9 ℃,最低-18 ℃,试验时间段气温均在-10~-13 ℃,试验中渠水出水口温度始终控制在0.2~0.4 ℃,井水水温均控制在13.4 ℃。
将所测得各断面的冰花密度绘制成柱状图如图2所示。图2为在同一注水温度,注水点在32 m处、井水流量分别为0.06、0.12和0.18 L/s,只改变渠水流量时冰花密度的沿程变化。
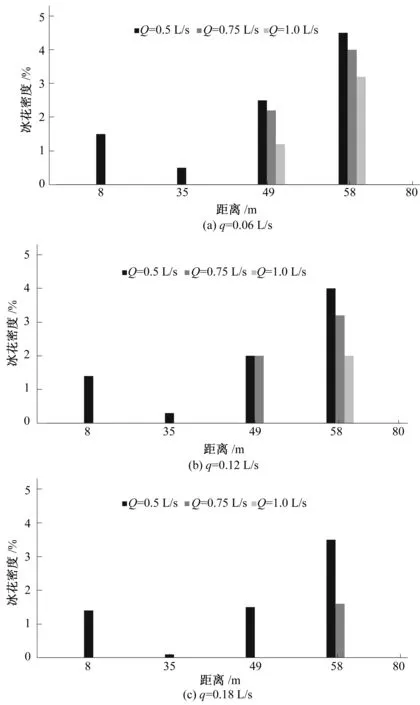
图2 不同渠水流量下冰花密度变化Fig.2 Ice density change under different canal water flow
图2是在保持井水流量、渠水流速等条件不变,只改变渠水流量时冰花密度的变化。从图2(a)中可以看出当q=0.06 L/s,Q=1.0、0.75和0.5 L/s时在渠末的冰花密度为1.2%、4.0%和4.5%,说明渠水流量越小,冰花密度越大,整个渠道产生的冰花越多,冰花初出现的也就越早。结合图2来看,渠水流量越小的,在8 m处就已经产生了较多的冰花,当32 m处的井水注入后,较高水温的井水将渠道内已经产生的冰花大量融化,因此在35 m处时,均只有少量冰花,随着热量的损失再逐渐产生冰花。
综上可知,在井水注入之前渠水流量相对较小时先开始产生冰花,说明渠水流量愈大,水温的沿程损失也就愈小。因为有较高温度的井水注入,所以已经产生的冰花部分被融化,冰花密度明显减小;随着水流的流动,热量继续散失,渠水流量相对较小的产生冰花的速度也相对较快。而注入的井水流量越大,冰花在所取试验断面中所占的密度就越小。由此可见,当其余各影响因素保持不变时,所输送的渠水流量越大,不冻长度的距离越长。
2.1.2井水流量对不冻长度的影响规律
在渠水流量、流速以及水温等因素保持不变,只改变井水流量,研究其对不冻长度的影响,方法与2.1.1方法相同。该试验进行时间为3 d,气候温度最高-12 ℃,最低-18 ℃,试验时间段气温均在-13~-16 ℃,试验出水口温度始终控制在0.2~0.4 ℃,井水水温均控制在13.4 ℃。
将该条件下所测得各断面的冰花密度绘制成柱状图如图3所示。图3分别为在同一注水温度,注水点在32 m处、渠水流量为1.0、0.75和0.5 L/s时,只改变渠水流量时冰花密度的沿程变化。
图3所示是在改变井水流量时,保持渠水流量和流速等因素不变,渠道内冰花密度的变化情况由图3(a)中可以看出,在8 m处和35 m处,均无冰花产生,说明该情况下渠水流量自身很大,降温结冰速度较慢,可能在注水位置前有冰花产生,但是井水注入后,温度提高,热量增加使得所产生的冰花全部融化,直到热量损失到一定程度,才开始慢慢地在不同井水流量下产生冰花。对比图3,可以看出在图3(c)中,8、35、49和58 m处3种不同的井水流量都产生了冰花,且数量较多。说明井水流量越小,冰花形成速度越快,其对应的渠道的不冻长度也就越短。

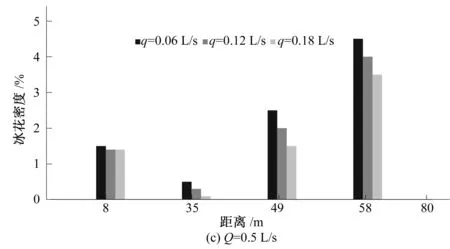
图3 不同抽水流量下冰花密度变化Fig.3 Ice density change under different well water flow
2.1.3渠水流速对不冻长度的影响规律
流速是水内冰生成、演变、输移的主要动力因素。当渠道流速大于临界输冰流速时,由于水流的紊动和拖曳作用,水面上的冰花不会相互黏结形成冰盖。随着冰花越结越多,速度低于了临界输冰流速,最终形成冰盖。因此在注水点后,随着热量的注入,有效减少了冰花,增加渠水流速,使水内冰花密度有所减小。该试验进行时间为3 d,气候温度最高-15 ℃,最低-21 ℃,试验时间段气温均在-17~-19 ℃,其余温度保持同上,通过分析数据,将冰水合流速在注水前后变化过程用折线图绘制在图4中。
图4所示为不同情况下渠水流速的变化示意图。图4可以看出不注入井水时,流速随着距离的逐渐增加越来越慢,图4(a)中,当Q=0.5 L/s时,冰水合流速由0.153 95 m/s降到0.055 95 m/s,Q=0.75 L/s时,冰水合流速由0.225 2 m/s降到0.142 55 m/s;Q=1.0 L/s时,冰水合流速由0.302 15 m/s降到0.227 m/s。可以看出流速的大小是随着流量的变化而变化的,流量越大则流速越大。结合图4可知,其变化规律和流量变化规律一样,流速越小,冰花密度越大,不冻长度的距离越短,反之越长。

图4 不同情况下渠水流速变化Fig.4 The change of canal water flow rate in different situations
2.2 热力条件对不冻长度的影响规律
在渠水流量、井水流量、渠水流速等因素均保持不变,只改变水温时,对不冻长度的影响。我们知道在冬季寒冷的气温下,渠水水温越低,渠水中越容易产生冰花,成为冰水混合物。渠水温度越低,其冰花产生速度越快,不冻长度相对就越短。而试验中所注入的井水均来自试验大厅,井水的温度无法调整一直保持在13.4 ℃左右。但是井水温度对不冻长度影响的原理与渠水温度对不冻长度影响的原理基本一样。井水温度越高,注入渠道内后与渠水混合,水温提升幅度也就高,然其混合后的水温变化即是渠水温度的变化规律。
2.3 气候条件对不冻长度的影响规律
在渠水流量、井水流量、渠水流速、水温等因素均保持不变,只改变气候条件的影响因素时,对不冻长度的影响。渠道水流的表面温度变化,是水气界面复杂的热力交换过程。而气候对水温也有一定的影响。气象要素(温度、降水、风等)的各种统计量是表述气候的基本依据。因为空气是直接与水体相接触的,并且以长波辐射和感热交换的方式直接作用于水体,影响水面温度的变化,因此,气温对水温的影响一般来说是最大的,同时也是最重要的。本次观测期内多次观测气温与水温的相关关系如图5所示。整个试验阶段,尽量避开了降雪的日子,没有降雪因素的影响;当地整月平均风速为7 m/s,且试验模型四周被楼环绕,基本没有风的影响。
由图5可知,在-9~-27 ℃时,渠道中水的温度逐渐降低,其温度单位长度下降的幅度由0.02 ℃提升到0.035 ℃,在室外气温越来越低时,由于气温与渠水表层温度差增大,表层水面温度和气温的热交换量增加,加快了水表面的热损失,水温单位长度下降的幅度升高。当气温为-27 ℃时,单位长度的渠水水温下降幅度最大。通过图5拟合出气温与单位长度下水温下降幅度为指数关系,关系式y=0.013 8 e-0.035 x,且R2为0.94,拟合度较高。
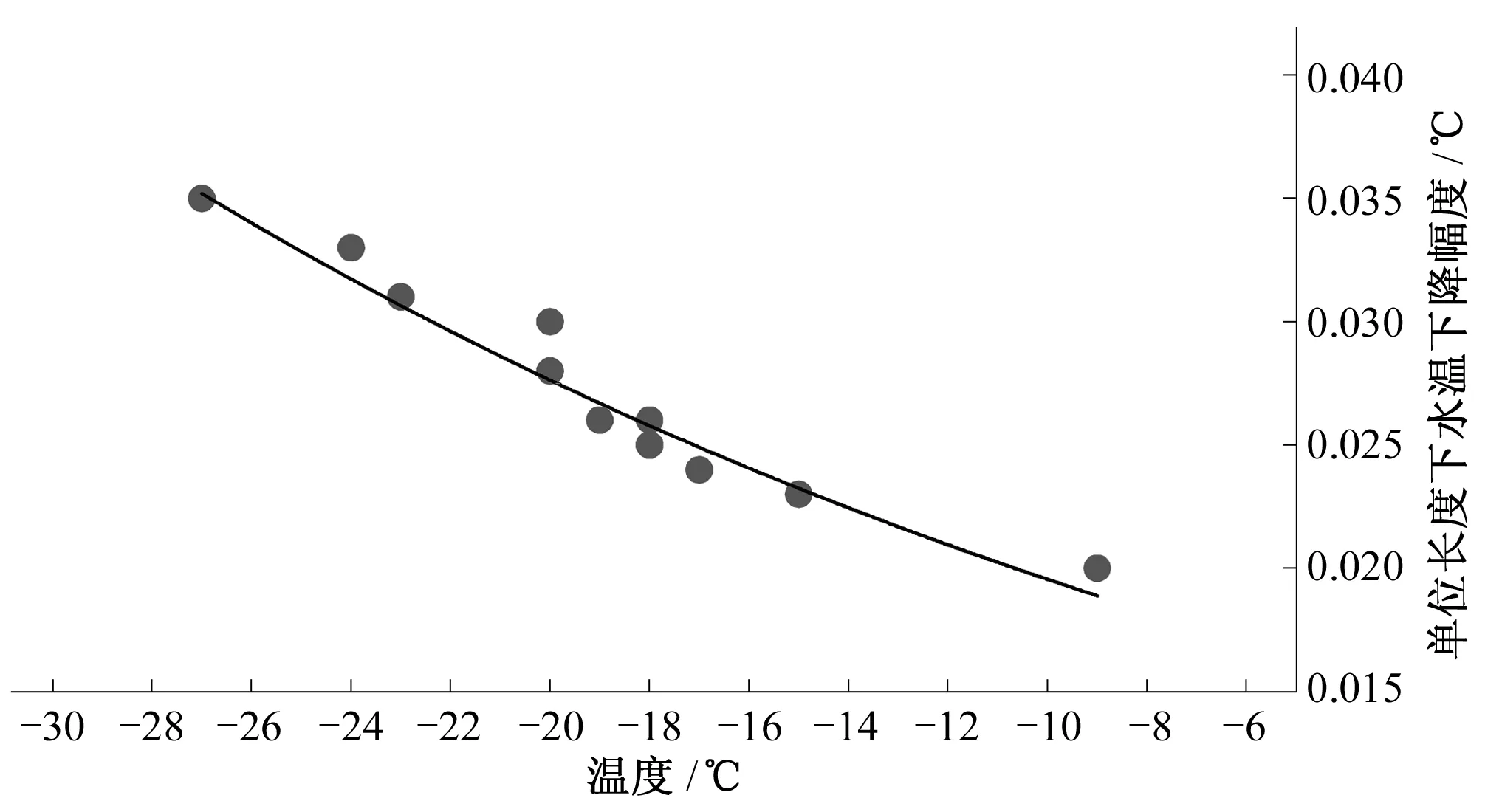
图5 气温与水温的关系Fig.5 Correlation between air temperature and water temperature
图6所示则为渠末冰花密度与大气温度的关系图,从图6可以看出其关系并拟合得出相应的关系式。图6中所示为不同气温下渠道最终断面的表层水域中冰花密度的变化。冰花的密度在-20 ℃以前均维持在很低的水平,基本保持在2.0%~2.5%的范围内,然而随着气温由-9 ℃降至-27 ℃时,渠末最终的产冰量增加,冰体积分数逐渐增大到4.5%。可知在不同的低气温情况下,冰花初出现的位置也逐渐在移动,才给冰花的大量产生提供了条件。通过图6拟合出气温与渠末端的冰花密度为非线性关系,关系式y=-0.009 1x2+0.164 1x+2.491 6,且R2高达0.95,拟合度高。

图6 气温与冰花密度的关系Fig.6 Correlation between air temperature and ice density
2.4 引水渠道不冻长度定量关系式
由2.3可知大气温度与单位长度水温的下降幅度为指数关系,又因为当过水断面面积接触冷空气越大,水温的降温速度越快,不冻长度距离会缩短,所以确定出过水断面和气温与不冻长度的关系:
(1)
式中:A为过水断面面积,m2。
参考邓朝彬[9]等总结的青海香加水电站的经验公式:
(2)
式中:K为与流量成正比的综合系数,K=0.64~1.00;e为热损失强度,e=0.085~0.105 kW/m2。
由此知道渠水流量、井水流量和渠水温度、井水温度与不冻长度成正比。因此综合上述水力条件、热力条件和气候条件,推导不冻长度的关系式,得出如下关系式:
(3)

(4)
式中:c为修正系数。
公式(2)适用范围为小流量Q<4 m3/s,气温为-20~-25 ℃条件下较为准确[48]。与本次试验的环境条件、水力条件等符合,因此根据公式(2)确定出式(3)的修正系数c=1.81。
公式(3)的计算结果与前人总结出的经验公式(2)的计算结果对比如图7所示。在热力条件和气候条件一致的情况下,9种工况分别如表2所示。

图7 推导公式计算结果与经验公式计算结果对比Fig.7 The comparison with derivation formula and empirical formula

表2 9种不同流量组合 L/s
从图7可以看出,所推导的公式与前人计算的经验公式计算结果最大误差为3.17%,最小误差为2.33%,拟合较好。因此在流量Q<1.0 L/s,外界温度低于0 ℃的情况下,该推导公式可用。
运用模型所修建的渠道端面,假设气温-20 ℃,渠水流量为0.5 L/s,井水流量为0.06 L/s,即最小渠水流量和最小井水流量的组合。在注入了第一口井后,结合所推导的公式,可以得知,正常情况下不冻长度应为40.85 m,即在整个渠道的56 m处,考虑到冰花会聚集,形成岸冰及冰盖,因此可以将第二口井布置在40~45 m处,可以保证在渠水到达第二个注水点处时热量已基本全部散失。而当渠水流量为1.0 L/s时,井水流量为0.18 L/s,即最大流量的组合时,不冻长度为86.08 m,考虑到沿程会形成的影响渠水流动畅通的因素,可将第二口井布置在75 m处。
3 结 语
抽水融冰中井水一旦注入渠水后,渠水水温会迅速提高,井水的注入对渠道水温有明显增温效果,能保证引水渠道冬季运行畅通,解决寒冷地区引水渠道冰封冰冻问题;根据试验结果,得到主要结论如下。
(1)水力条件。若只改变渠水流量,所输送的渠水流量越大,水体总热量越高,散失热量不大,其不冻长度的距离越长,反之越短;若只改变井水流量,所注入的井水流量越大,其不冻长度的距离越长,反之越短;若只改变流速,所测得的渠水、井水和混合后水流的流速越大,其不冻长度的距离越长,反之越短。
(2)热力条件。渠水、井水、混合后水温的温度越高,冰花产生速度越慢,不冻长度距离越长,反之越短。
(3)气候条件。室外气温越低,表层水面温度和气温的热交换越快,水表面的热损失越快,水温沿程降幅度升高,最终的产冰量和冰体积分数逐渐增大,给冰花大量产生提供了条件,增大了产冰量,缩短了不冻长度,反之不冻长度距离变长。
(4)得出了相关的不冻长度关系式,通过该式计算结果与已有经验公式进行比较,发现拟合较好。
□
[1] 黄酒林,宗全利,刘贞姬,等.高寒区引水渠道抽水融冰原理及原型试验[J].石河子大学学报(自然科学版),2014,15(6):392-396.
[2] 李克锋,郝红升,庄春义,等.利用气象因子估算天然河道水温的新公式[J].四川大学学报(工程科学版),2006,38(1):1-4.
[3] 吴剑疆,茅泽育,王爱民,等.河道中水内冰演变的数值计算[J].清华大学学报,2003,43(5):702-705.
[4] 王晓玲,周正印,蒋志勇,等.考虑气温变化影响的引水渠道水内冰演变数值模拟[J].天津大学学报,2010,43(6):515-522.
[5] Hung Tao Shen,Lianwu Liu. Shokot su river ice jam formation[J]. Cold Regions Science and Technology, 2003,37:35-49.
[6] P H Wadia. Mass transfer from sphere and discs in turbulent agitated vessels[D]. Department of Chem ical Engineering, Massachusetts Institute of Technology, 1974.
[7] G K Betchelor. Mass transfer from small particles suspended in turbulent fluid[J]. Journal of Fluid Mechanics,1980,98:609-623.
[8] 邓朝彬,刘柏年.香加水电站引水渠冬季注水升温运行发电实践经验介绍[J].农田水利与小水电,1987,(7):43-45.
[9] 辛向文,周孝德.天然水温估值计算方法研究[J].水资源与水工程学报,2010,21(2):124-127.
[10] 王 峰,吴艳华,马月俊,等.红山嘴梯级水电站抽水融冰技术应用与探讨[J].河南水利与南水北调,2009,(7):111-112.
[11] 王文学,丁楚建.抽井水入发电渠道冬季运行试验及其计算[J].农田水利与小水电,1991,(12):35-41.
[12] 王燕燕,刘焕芳,王 振.桩柱式双丁坝局部水流结构及冲淤规律的试验研究[J].石河子大学学报(自然科学版),2013,15(2):103-108.
[13] 蒲 灵,李克锋,庄春义,等. 天然河流水温变化规律的原型观测研究[J].四川大学学报(自然科学版),2006,43(3):614-617.
[14] 铁 汉.寒冷地区水电站引水明渠冬季不结冰长度计算[J].西北水电,1999,(1):23-24,61.
