弧底梯形渠道无喉道量水槽水力性能影响因素研究
2016-03-23杨珮珮马孝义钟新铭西北农林科技大学水利与建筑工程学院陕西杨凌712100
杨珮珮,马孝义,钟新铭(西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100)
在农业生产过程中,实施科学的水资源管理必须依赖于对水位流量数据的精准计量,灌区量水正是提供这些资料的有效手段。高效农业的发展以及水价制度的改革,迫切需要一种结构简单、设计合理、精度高的渠道量水设施。无喉道量水槽由于没有喉道,上游壅水小,不易淤积堵塞,且在淹没出流的情况下,上游水面波动小,量水精度较高,在生产实践中得到广泛应用[1]。
目前,无喉道量水槽的研究主要局限于矩形渠道无喉道量水槽[2]和U形渠道抛物线形无喉道量水槽[3,4],针对弧底梯形渠道还缺乏相应的量水设施研究。弧底梯形渠道不仅基本具备水力最佳断面,水流条件好,断面曲线平滑,更适应北方寒冷地区因渠底土体高含水量所产生的冻胀变形及冻害破坏,在北方灌区和输水工程中得到广泛应用[5]。随着计算机技术的迅速发展以及计算方法的优化改进,利用计算流体动力学(CFD)对物理模型进行数值模拟被越来越多的采用[6]。朱亚磊等[7]采用RNGk-ε湍流模型对平坦V形量水堰进行数值模拟,得到不同条件下相应的流场,结果表明数值模拟方法能够准确模拟明渠三维水流特性。吉庆丰,袁晓渊等[8]采用RNGk-ε湍流模型及VOF方法处理自由水面,数值模拟了梯形渠道圆柱形量水槽三维水流运动,通过对多个流量情况的计算,获得了驻点水深、水面位置、三维水流流态等量水槽水力特性。现有的研究成果均表明数值方法可以准确模拟量水槽内部流场及各项水力特性,但对其水力性能的影响因素还缺乏深入研究。本研究针对弧底梯形渠道提出了一种新的无喉道量水槽,并采用RNGk-ε湍流模型和VOF方法相耦合,对弧底梯形渠道无喉道量水槽进行三维数值模拟,并从渠道比降和喉口收缩比等方面对量水槽的水力性能进行分析,以确定其水力性能与各影响因素之间的关系,为量水槽的进一步研究及其优化推广提供了新思路。
1 无喉道量水槽物理模型与方案设计
1.1 量水槽物理模型
弧底梯形渠道无喉道量水槽由进口收缩段,出口扩散段以及喉口三部分组成,通过调整喉口断面弧底半径R,使量水槽形成侧收缩,收缩比为ε=A0/A,即喉口断面面积A0与渠道断面面积A之比。当水流通过量水槽收缩段时,过流断面缩窄,只要喉口宽度合理,便可以产生平稳的水面跌落,使下游水流在相当大的范围内不会影响上游水流,从而形成单一稳定的水位流量关系,以达到测流的目的。弧底梯形渠道无喉道量水槽结构如图1所示。
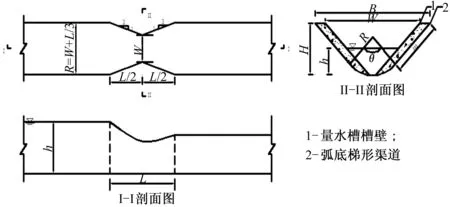
图1 弧底梯形渠道无喉道量水槽结构示意图Fig.1 Structural of arc-based trapezoidal canal and cut-throat flow measurement flume
图1中:W为量水槽喉口宽度,L为量水槽长度,B为渠顶宽度,H为渠道高度,h为上游水深,θ为渠道底弧圆心角,R为渠道底弧半径,m为渠道边坡系数。
1.2 数值试验方案与设计
试验选取4种不同收缩比的量水槽在不同底坡范围内进行综合数值试验模拟研究,以期验证数值模拟的可行性,确定量水槽的水力性能与各影响因素之间的关系。渠道参数及数值试验方案如表1所示。

表1 渠道参数及数值试验方案Tab.1 Parameters of arc-based trapezoidal canal and cut-throat flow measurement flume
2 数学模型
2.1 数值计算方法
本文采用RNGk-ε湍流模型封闭雷诺时均应力方程,VOF方法追踪自由液面,其基本控制方程[6]如下所述。
2.1.1连续性方程和N-S方程
一般来讲,对于不可压缩黏性流体运动,根据基本物理守恒定律,过槽水流为牛顿流体,则量水槽测流可用连续性方程和Navier-Stokes方程[9]描述。
连续性方程:
(1)
Navier-Stokes方程:
(2)
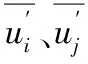
2.1.2RNGk-ε模型
RNGk-ε湍流模型通过修正湍动黏度,可以更好的处理高应变率及流线弯曲程度较大的流动,湍动能方程k及湍动耗散率方程ε为:
(4)
式中:μt为湍动黏度,可由k、ε求出:
(5)
Gk是由于平均速度梯度引起的湍动能k的产生项,由下式计算:
(6)
在ε方程中增加了一项,从而反映了主流的时均应变率Eij:
(7)
(9)
其中Cu=0.084 5,αk=αε=1.39,C1ε=1.42,C2ε=1.68,η0=4.377,β=0.012。
2.1.3VOF模型
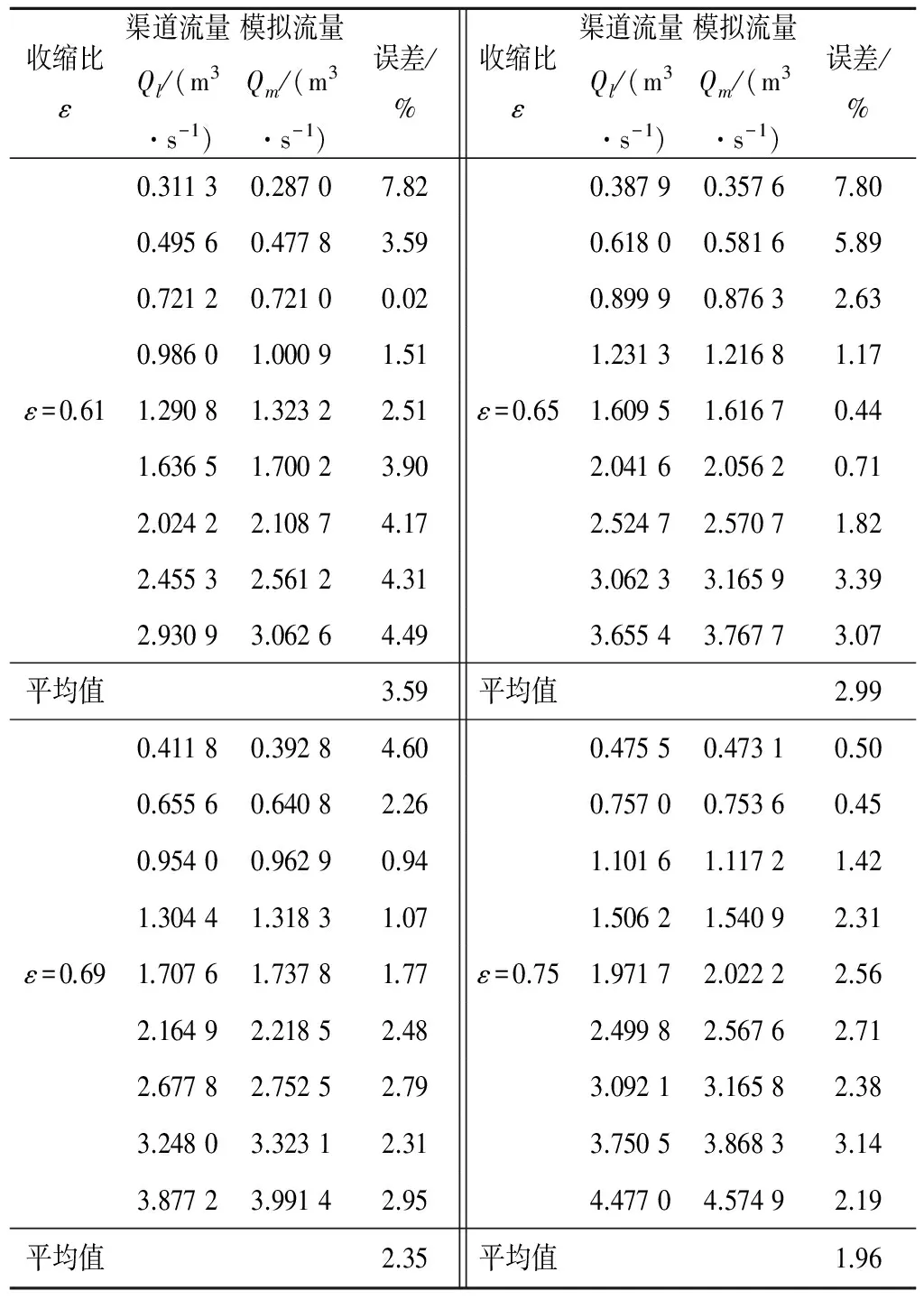
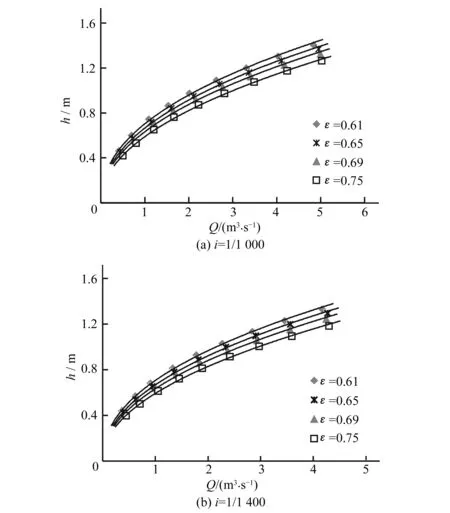
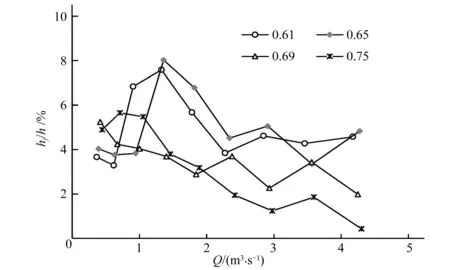
VOF(The Volume of Fluid)模型是通过求解单独的动量方程和处理穿过区域的每一流体的容积比来模拟两种或三种不能混合的流体。在水气二相流中,假设函数aw和aa分别代表计算域中每一控制单元内水和气的体积分数,则aw=0,0 aw+aa=1 (10) 其体积分数可根据如下连续性方程实现: (11) 式中:ui和xi分别为速度分量和坐标分量。 本数值模拟试验选取渠道长30 m左右,以量水槽为原点,上下游各取渠长15 m进行研究。坐标原点取在渠道进口断面圆弧中心点处,取渠道顺水流方向为x轴正方向,沿宽度方向向左为y轴正方向,沿高度方向向上为z轴正方向。本文通过matlab选型,初步选取0.61,0.65,0.69和0.75四种收缩比进行数值试验,利用AUTOCAD建立三维几何模型,将所建模型导入到Gambit中进行网格划分。为使渠道内水流模拟逼真,对整个模型采用计算精度较高的六面体非结构网格进行划分,并对量水槽段采用局部加密网格处理,由于渠道左右对称,故对计算域取一半进行研究,网格总数约为3.0×105个。与四面体混合网格相比,六面体非结构网格产生的数值耗散更小,能够有效降低数值模拟的误差。 2.3.1计算方法 本文采用隐式VOF方法追踪自由液面,RNGk-ε湍流模型封闭雷诺时均N-S方程,有限体积法对控制方程进行离散,离散格式采用稳定性较高的一阶迎风(First-Order-Upwind)格式,压力速度耦合采用瞬态PISO算法。设置进出口质量流量(Mass Flow Rate)监测器,求解变量的收敛判据均为0.000 1,当监测曲线的值基本保持不变时认为计算收敛。 2.3.2边界条件 渠道进口边界分为上部的空气入口和下部的水入口,分别给定边界条件为压力入口(PRESSURE INLET)和速度入口(VELOCITY INLET),出口边界条件给定压力出口(PRESSURE OUTLET),在边界条件中设置各项的湍流参数,可根据如下公式求得。 湍动能k的计算式: (13) 湍动能耗散率ε的计算式: (14) 式中:Cμ取0.09;l为湍流长度尺度;L为关联尺寸,可取水力直径,l=0.07L。 渠道整个底部及边壁选择固壁边界条件(WALL),并设置无滑移选项,近壁面采用标准壁函数法处理。以ε=0.69为例,在底坡i=1/1 000和1/1 800范围内湍流参数设置如表2所示。 表2 弧底梯形渠道无喉道量水槽湍流参数表Tab.2 Turbulence parameters of arc-based trapezoidal canal and cut-throat flow measurement flume 为了检验数值模拟的准确性和可靠性,本文根据选定的设计水深(h=0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1、1.2 m),运用理论流量公式计算出相应渠道流量。读取控制断面的水位和流速数据,并依此计算相应模拟流量,将模拟流量与渠道流量进行对比分析。量水槽流量与渠道流量对比见表3。 表3 渠道流量与模拟流量的对比分析Tab.3 Analysis of measured flow and simulated flow 从表3可以看出,当ε=0.61和0.65时,小水位测流误差较大,其余模拟结果与计算结果误差均控制在较小范围内,平均误差为2.72%,满足灌区要求的测流精度(<5%)。从而说明数值模拟具有一定的可靠性。 以i=1/1 000和i=1/1 400为例,不同喉口收缩比时水位与流量关系见图2(a)、(b)。从图2可以看出,各收缩比下的水位流量呈现良好的指数相关关系,相关系数可达0.999。同一渠道比降下,不同收缩比对量水槽自由出流流量影响较大,随收缩比的增加,水位与流量关系曲线下移。 图2 不同收缩比下的水位流量关系Fig.2 Relationship between water level and discharges under different contraction ratio conditions 研究底坡在1/800~1/3 500范围内水位流量的变化规律,可知量水槽在一定底坡范围内可形成单值稳定的水位流量关系。如图3(a~d)所示,ε>0.75时,1/800~1/1 400坡降范围内难以形成统一的Q~h关系;ε=0.75时,1/800~1/1400坡降范围内,量水槽具有统一的Q~h关系;ε=0.69时,1/1 000~1/1 800坡降范围内,量水槽具有统一的Q~h关系;ε=0.65时,坡降范围可扩大至1/1 000~1/2 000;ε=0.61时,最缓坡降可达1/3 500。可见随收缩比的减小,量水槽逐渐在较大底坡范围内形成统一的Q~h关系且最大收缩比不宜超过0.75。 图3 不同底坡下的水位流量关系Fig.3 Relationship between water level and discharges under different bottom slope conditions 为了保证测流精度,量水槽上游渠道的流速水头不应太大,避免水流在接近量水槽处形成驻波,而无法精确的读出上游水深,因此明渠测流规范要求上游渠道弗劳德数Fr要小于0.5[10]。本文研究了i=1/1 400时不同收缩比情况下Q~Fr关系和ε=0.61时不同底坡情况下的Q~Fr关系。研究结果见图4和图5。从图4可以看出,随着收缩比增大,弗劳德数逐渐增大,同一收缩比下,弗劳德数随流量呈缓慢增加的趋势,但最大值不超过0.5。从图5可以看出,在流量一定时,弗劳德数随底坡增大变化不大,且小流量时弗劳德数变化较大。因此,上游断面弗劳德数与量水槽收缩比有关,应选择相对较小的收缩比,从而不影响测流精度。 图4 不同收缩比下弗劳德数与流量关系Fig.4 Relationship between froude number and discharge under different contraction ratio conditions 图5 不同底坡下弗劳德数与流量关系Fig.5 Relationship between froude number and discharge under different bottom slope conditions 由于渠道过流断面的减小,与原有渠道相比,在渠道内设置量水槽后势必造成一定的上游壅水。实践表明渠道壅水高度应有一个合理的范围,过大的上游壅水可能造成流速降低进而促使渠道产生淤积,同时需要加高渠堤,还会增大水面蒸发面积。过小的上游壅水可能影响临界流的发生[11]。表4为不同收缩比及底坡下壅水高度的变化规律。 由表4可知,收缩比和底坡一定时,随着流量增大,量水槽上游壅水高度也逐渐增大,且小流量时壅水高度变化较大,大流量时基本不变。同一收缩比流量不变时,量水槽上游壅水高度随底坡的变缓而逐渐减小。在渠道底坡i=1/1 200,收缩比ε=0.75时,上游壅水高度变化范围为0.72~1.81 cm,壅水高度较小,过小的上下游水位差会导致喉口附近不易形成临界流。小底坡下收缩比越小,量水槽的上游壅水高度越大,在渠道底坡i=1/1 000,收缩比ε=0.65时,上游壅水高度最高可达16.91 cm,壅水较大,易导致水头损失的增加从而影响量水槽的测流精度。综上所述,量水槽合理收缩比的选择应视渠道底坡而定,底坡较小的渠道应选取较大的收缩比,底坡较大的渠道应选取较小的收缩比,同时为保证测流精度,底坡较大时可适当缩小测流范围,本文研究的大渠道量水槽具有较宽的自由出流范围,其适宜测流范围为0.27~5.63 m3/s。 水流在通过弧底梯形渠道无喉道量水槽时,由于侧收缩的存在,速度沿水流方向增加,由于水流的混掺碰撞产生了局部水头损失,由渠槽边壁摩擦产生的沿程水头损失远小于局部水头损失,因此可以忽略不计。将上游观测断面至量水槽入口段、量水槽收缩段和出口扩散段作为一个整体研究量水槽的局部水头损失,根据数值试验结果,提取上游水深和下游水深,上游断面平均流速和下游断面平均流速来研究量水槽收缩比对上下游水头损失的影响。图6反映了底坡i=1/1 400时不同喉口收缩比下量水槽的水头损失占上游总水头的比例(相对水头损失),结果显示,当喉口收缩比为0.61~0.75时,不同流量下的相对水头损失无明显变化规律,但平均相对水头损失随收缩比的减小而变大,这是因为收缩比越小,使得侧收缩越大,边界条件急剧变化,水流混掺作用更加强烈,局部水头损失增大。同一收缩比时,除个别观测点外,量水槽的相对水头损失随流量的增大而变小,且这种趋势在大收缩比时比较明显,这是因为量水槽侧收缩变小,槽身阻水能力减小,从而局部水头损失变小。无喉道量水槽相对水头损失最小值为0.43%,最大值为8.61%,水头损失平均占上游总水头的4.13%,小于长喉道量水槽的13%。 表4 不同条件下上游壅水高度Tab.4 Upstream backwater height under different conditions 图6 不同收缩比和流量下量水槽的水头损失占上游总水头的比例Fig.6 Relative head loss under different contraction ratios and discharges conditions 本文采用RNGk-ε湍流模型和VOF方法相耦合,对弧底梯形渠道无喉道量水槽进行了三维数值模拟,分析了渠道比降和喉口收缩比与量水槽水力性能的关系。将模拟流量与渠道流量进行对比分析,得出测流平均误差为2.72%,表明该数值模拟方法有效可行;喉口收缩比与渠道比降对形成单值稳定的水位流量关系有较大的影响,随着收缩比的减小,量水槽逐渐在较大的底坡范围内形成统一的水位流量关系;上游断面弗劳德数随渠道流量的增加缓慢增加,但最大值不超过0.5,满足灌区测流要求;适宜喉口收缩比的选择应视渠道底坡大小而定,底坡较小的渠道应选取较大的收缩比,底坡较大的渠道应选取较小的收缩比;量水槽平均相对水头损失为4.13%,水头损失较小。针对弧底梯形渠道提出的弧度梯形无喉道量水槽结构简单,适用性强,各项性能指标均满足测流要求,为量水槽的进一步研究及其优化、推广提供了新思路。 □ [1] 马孝义. 北方旱区节水灌溉技术[M]. 北京: 海潮出版社, 1999. [2] 尹京川, 马孝义, 胡杰华, 等. 矩形无喉段量水槽水力特性数值模拟研究[J]. 中国农村水利水电, 2011,(6):98-100. [3] 王 智, 朱凤书, 刘晓明. 平底抛物线形无喉段量水槽试验研究[J]. 水利学报, 1994,(7):12-23. [4] 郝晶晶, 马孝义, 王波雷, 等.基于VOF的量水槽流场数值模拟[J]. 灌溉排水学报, 2008,(2):26-29. [5] 滕 凯, 张丽伟. 弧底梯形明渠临界水深的简化计算法[J]. 长江科学院院报, 2013,(5):60-63. [6] 王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. [7] 朱亚磊, 马孝义, 战国隆, 等.平坦V形量水堰的数值模拟[J]. 人民黄河, 2010,32(6):98-101. [8] 吉庆丰, 袁晓渊, 葛 蕴, 等. 梯形渠道圆柱形量水槽水力特性数值模拟[J]. 灌溉排水学报, 2012,(2):59-61. [9] 刘 英, 王文娥, 胡笑涛, 等. U形渠道圆头量水柱测流影响因素试验及模拟[J]. 农业工程学报, 2014,(19):97-106. [10] 于 佳. 机翼形量水槽标准化试验研究与数值模拟[D]. 陕西杨凌:西北农林科技大学, 2011. [11] 潘志宝. 机翼形量水槽水力特性试验与数值模拟研究[D]. 陕西杨凌:西北农林科技大学, 2009.2.2 几何模型与网格划分
2.3 计算方法与边界条件
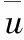

3 计算结果与分析
3.1 模型验证
3.2 不同收缩比下的水位流量关系
3.3 不同底坡下的水位流量关系


3.4 不同收缩比及底坡下弗劳德数变化规律


3.5 不同收缩比及底坡下壅水高度变化规律
3.6 不同收缩比下水头损失变化规律

4 结 语
