水稻水肥耦合效应研究
2016-03-23林彦宇聂堂哲
张 超,林彦宇,聂堂哲
(东北农业大学农业部农业水资源高效利用重点实验室,哈尔滨 150030)
水和肥是水稻生长过程中最重要的两大影响因子[1,2],但在生产中如果不合理利用这两大资源,不仅会造成资源的浪费,而且也会对环境造成严重的威胁,因此,水肥耦合效应的研究引起了国内外许多学者的关注与重视[3-5]。朱庆森等人对不同土壤水分状况下氮素对水稻产量的影响及其机理进行了研究,认为在轻度干旱下(土壤水势在-30 kPa),适当的增加施氮量有利于水稻产量的提高[6,7]。但以往的研究都集中在水肥单因子或水氮耦合方面,而对水肥多因子的互作效应并未做深入系统的研究。
目前,人工神经网络模型有很多种,BP(Back Propagation)[8]神经网络是人工神经网络的重要模型之一,应用极为广泛,其具有很好的分布存储性和容错性,非常适合解决非线性问题,而且在实测资料不够完备的情况下仍可以进行计算和预测;遗传算法(Genetic Algorithm,GA)[9]是一种新型的优化算法,能有效的利用历史信息来推断下一代期望性能有所提高的期望点集。这样一代代的不断进化最后收敛到一个最适应环境的个体上,求得问题的最优解,而基于实数编码的遗传算法(Real Coded Accelerating Genetic Algorithm,RAGA)[10]又克服了二进制编码的缺点,使算法的寻优能力大大加强;这两种方法都很适合求得非线性问题,但又有各自的缺点,BP网络的误差函数为平方型,存在局部极小值问题且收敛速度较慢;遗传算法在建立系统层次结构等方面有着独自的特点,但在学习、训练能力上远不如BP模型,因此将这两种模型有机结合起来,取长补短,可更准确、高效的求出最优值。
基于RAGA的BP模型在水文地质、食品医药等领域已广泛应用[11,12],但在作物水肥耦合研究方面,国内外研究还是很罕见。为了探讨水稻产量与水肥多因子之间的复杂关系,找出最优的水肥配施方案,本文选取施氮量、施钾量、施磷量、分蘖末期土壤含水率占饱和含水率的百分比4个设计因子,以产量为目标因子,在2011年和2012年进行了连续两年的盆栽试验,在2011年试验中,经RAGA-BP神经网络模型计算出的最佳水肥施入量,于2012年在相同条件下进行了试验验证,其预测结果在合理的试验误差范围内,表明此模型对生产实践具有指导意义,并对制定水肥配施方案提供相应的参考。
1 材料与方法
1.1 试验区概况
本试验在东北农业大学园艺试验站温室内进行,供试水稻品种为东农427。供试土壤为黑土,其基本理化性质如下:有机质28.56 g/kg、全氮1.45 g/kg、全磷0.78 g/kg、全钾20.76 g/kg、速效氮115.82 mg/kg、速效磷54.3 mg/kg、速效钾182.6 mg/kg、pH值为6.52,土壤体积饱和含水率为51.47%。
1.2 试验材料
供试肥料为尿素(含N46%)、 钾肥(含K2O 40% )、 磷酸二铵(含N18%,含P2O546% )。试验盆钵为可再生性密闭圆桶,上口直径30 cm,圆桶高30 cm,每桶装土15 kg,定苗4株。
1.3 试验方法
1.3.1二次饱和D-416最优设计
本研究采用二次饱和D-416最优设计[13]制定试验方案,选取施氮量、施钾量、施磷量、分蘖末期土壤含水率占饱和含水率的百分比4个因素为设计因子,编制因子水平编码表,见表1。试验共16个处理(见表3),每个处理重复5次,共计80次。
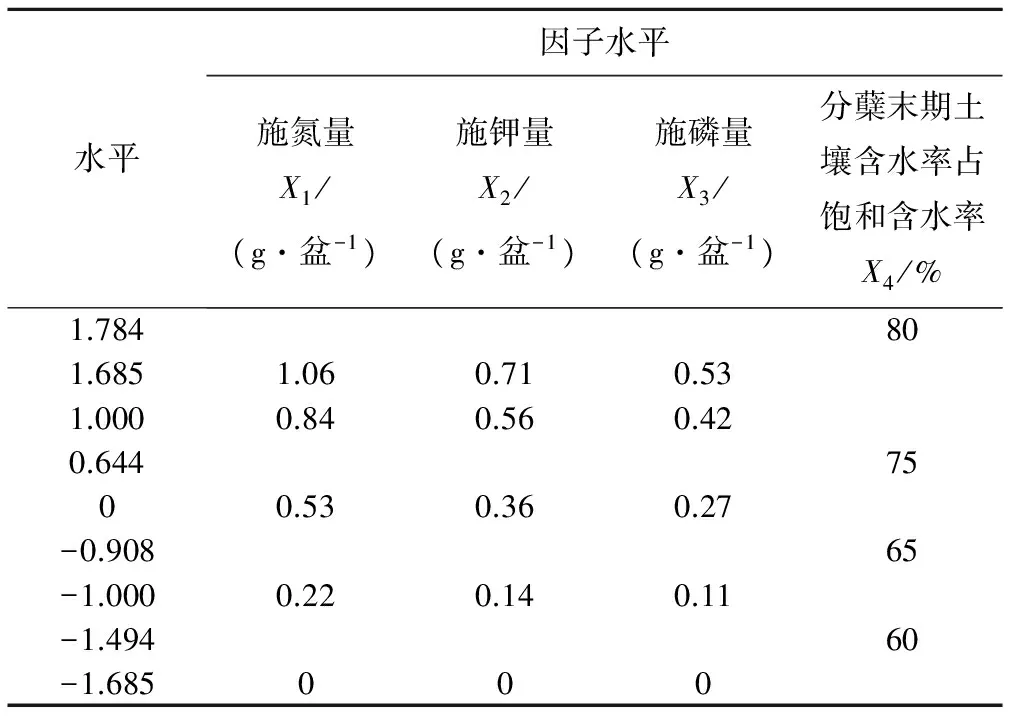
表1 因素水平编码表Tab.1 Factor level codes
施氮量为0~1.06 g/盆(折合公顷量为0~150 kg/hm2),比例为基肥:分蘖肥∶拔节肥∶穗肥=3∶3∶3∶1,基肥在插秧前施入;分蘖肥在水稻移栽后7~10 d施入;拔节肥在水稻的幼穗长1~2 mm施入;穗肥在抽穗后5~10 d施入。
施钾量为0~0.71 g/盆(折合公顷量为0~100 kg/hm2),施入比例为基肥∶穗肥=1∶1。
施磷量为0~0.53 g/盆(折合公顷量为0~75 kg/hm2),作为基肥一次性施入。
计算施入土壤中的化肥量,其计算公式为施肥量=推荐施肥量/化肥的有效含量。
以分蘖末期土壤含水率占饱和含水率的下限值作为基本设计参数,其他各生育时期与其的比例关系为分蘖(前∶中∶后) ∶拔节孕穗期(前∶后)∶抽穗开花期∶乳熟期=(1. 3∶1.15∶1)∶(1.15∶1.3)∶1.3∶1.15(见表2)[14]。

表2 各生育时期水分管理表Tab.2 Water management at different growth stages
注:分蘖后期晒田5~7 d;表2中单位为%的数字表示田间无水层情况下,土壤水分占饱和含水率的百分比。
1.3.2产量的测定
在成熟期应考种并测定其有效穗数、穗粒数、千粒重、结实率,最终计算理论产量。
(1)有效穗数。应查每一处理的结实的穗数,取其平均值。
(2)穗粒数。以每盆水稻计数,自然落干后统计其每穗粒数,然后计算出每一处理平均穗粒数。
(3)千粒重。将其晾晒干后使籽粒充分混合,任意取出3组,每组300粒,分别称重,当各组的质量相差不到3%时,平均重即为千粒重,如差值超过3%,再取300粒称重,用最为接近的3组数值平均值作为千粒重。
(4)结实率。将其晾晒干后使籽粒充分混合,任意取出3组,每组300粒,数其空瘪数,当各组的质量相差不到3%时,实粒数与总粒数的比值即为结实率,如差值超过3%,再取300粒数其空瘪数,用比值为最接近的3组数值平均值作为结实率。
(5)理论产量。产量=有效穗数×穗粒数×千粒重×结实率。
1.3.3RAGA-BP神经网络模型
RAGA-BP神经网络模型[15]寻优主要分为BP神经网络训练拟合和遗传算法极值寻优两步,算法流程如图1所示。
(1)输入层节点的确定。根据影响产量的主要因素施氮量、施钾量、施磷量、分蘖末期土壤含水率占饱和含水率的百分比等因素建立BP模型,这4个因素作为模型的输入节点。
(2)隐含层节点数的确定。隐含层节点数的确定由于没有明确的方法,其理论计算较为复杂,一般有如下公式来确定隐含层神经元个数的范围,即:
(1)
式中:l为隐含层节点数;n为输入节点数;m为输出节点数;a为1~10之间的调节常数。
本文通过计算隐含层节点数在3~12之间,然后通过不同神经元的网络进行训练对比,发现当网络的隐含层节点数为10时,网络具有足够的泛化能力和输出精度,且网络的训练步数较少,因此确定网络的隐含层节点数为10。
(3)输出层节点的确定。输出层节点的设置根据需要预测的性能参数来确定,在此网络中以产量作为输出节点。
(4)传递函数及算法。隐含层传递函数为Tansig和函数Logsig,输出层传递函数为Purelin。误差算法采用Levenberg-Marquardt,该算法较传统BP算法而言,其梯度下降要快得多,从而在整个网络的收敛上能以很少的迭代次数达到误差要求。
(5)遗传算法极值寻优。将训练后的BP神经网络预测结果作为个体适应度值,通过选择、交叉和变异操作寻找全局最优值时对应的输入值。
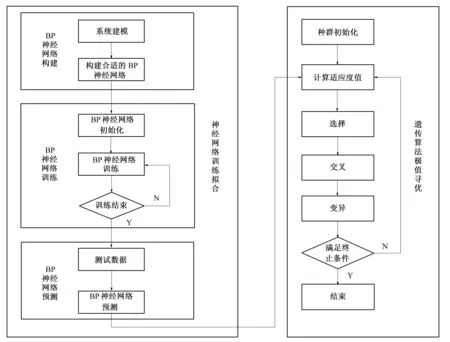
图1 算法流程图Fig.1 Flow diagram of algorithm
2 结果与分析
2.1 饱和设计结果与分析
依据表3试验结果可以看出,当施氮量为0.84 g/盆,施钾量为0.56 g/盆,施磷量为0.42 g/盆,分蘖末期土壤含水率占饱和含水率的75%时,水稻的产量最高,达72.34 g/盆。但由于二次饱和设计仅考虑这几个试验点间的部分试验结果,并未从整个条件区间进行考虑,存在偶然现象或容易忽略最优条件,所以本文尝试利用RAGA-BP神经网络来找出它们之间的变化关系,并最终求出最优值。
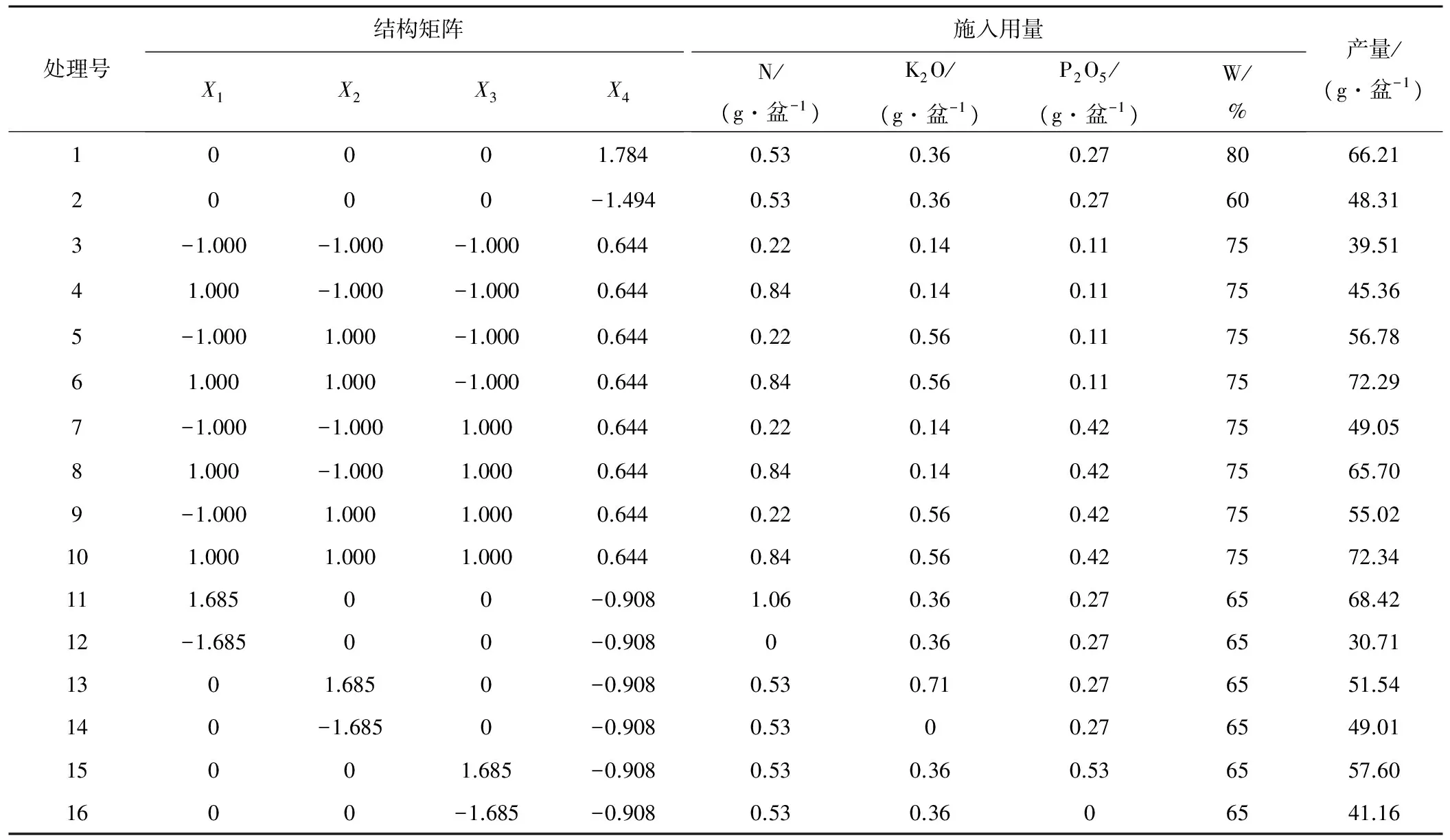
表3 二次饱和D-416最优设计表Tab.3 Quadratic saturation D-416 design Table
2.2 BP神经网络模型
用函数输入输出数据训练BP神经网络,使训练后的网络能够拟合非线性函数输出,保存训练好的网络用于计算个体适应度值。利用饱和试验设计中的16组数据作为神经网络的输入信号,对网络进行训练,选择最大训练次数500次,训练时间0.1 s,期望误差10-5,再通过训练后的神经网络对随机产生的16组数据进行预测,检查网络的外推性能,试验测得值与网络预测值结果如图2所示,预测误差如图3所示。从图2和图3可以看出,BP神经网络可以准确的预测非线性函数的输出,可以将网络预测输出近似看成函数的实际输出。
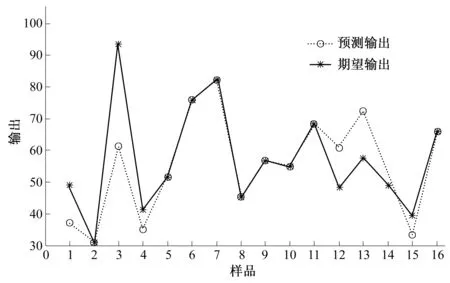
图2 BP神经网络预测Fig.2 BP neural network forecast
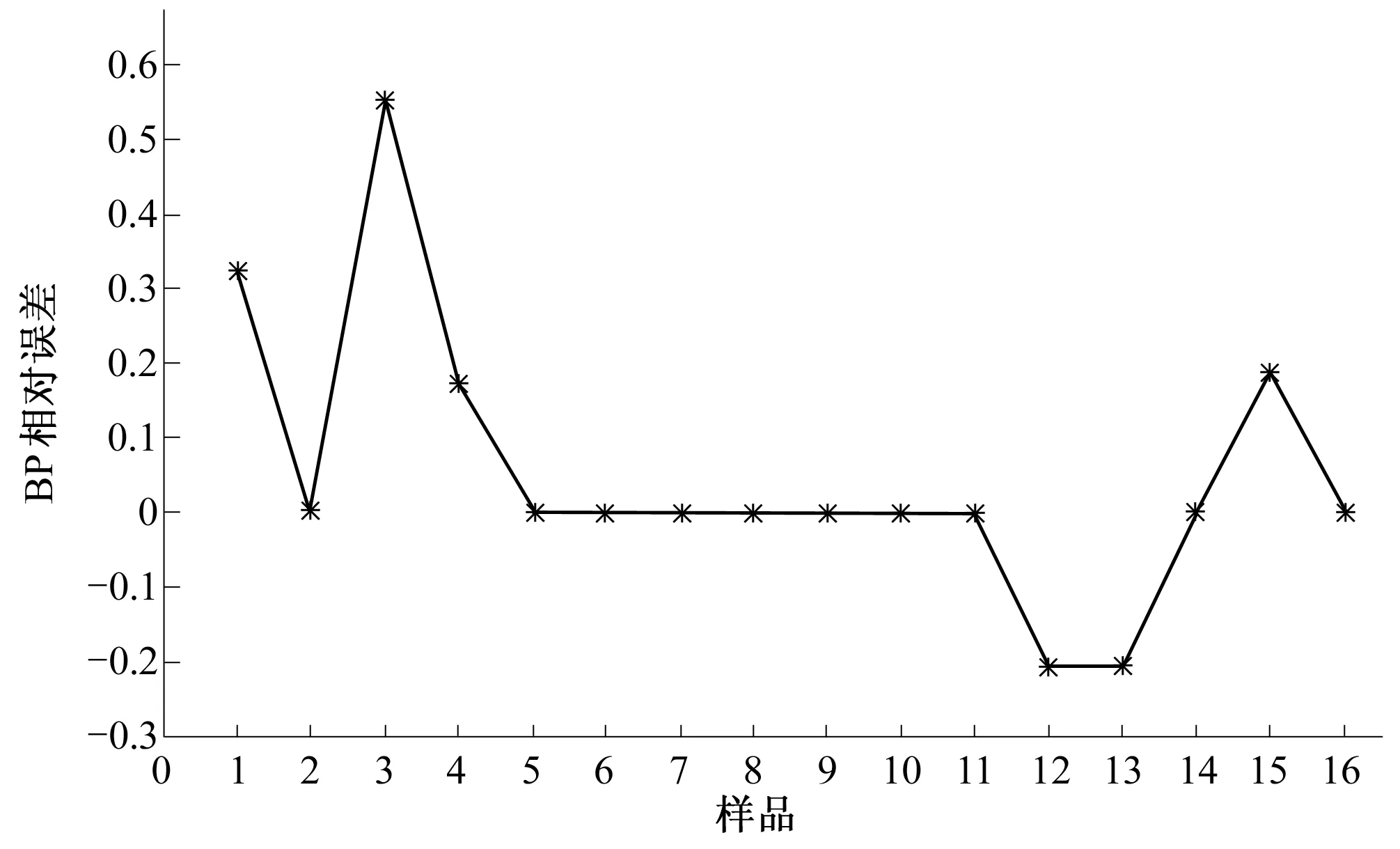
图3 BP神经网络预测误差Fig.3 Error of BP neural network forecast
2.3 遗传算法主函数
遗传算法采用实数编码的加速遗传算法(RAGA),由于寻优函数只有4个输入参数,所以个体长度为4,个体适应度值为BP神经网络预测值,适应度值越小,个体越优。本文RAGA中种群规模选为20,交叉概率0.4,变异概率0.2,进化次数100次。优化过程中最优个体适应度值变化曲线如图4所示。RAGA得到的最优个体适应度值为73.55 g/盆,对应的最优个体为,即施氮量为1.01 g/盆、施钾量为0.63 g/盆、施磷量为0.46 g/盆、分蘖末期土壤含水率占饱和含水率的75.2%;

图4 适应度变化曲线Fig.4 Changing curves of fitness
2.4 模型的验证
将RAGA-BP模型中得出的水肥参数在2012年度相同条件下进行试验与计算,得到的水稻产量实测值与预测值见表4,与模型的相对误差仅1.68%,说明基于RAGA-BP神经网络模型用于利用水肥施入量去预测水稻产量方面是可行的。
3 结 语
(1)通过二次饱和D-416最优设计结合RAGA-BP神经网络,得出水稻产量最高时最优水肥方案,即RAGA得到的最优个体适应度值为73.55 g/盆,对应的最优个体为,即施氮量为1.01 g/盆、施钾量为0.63 g/盆、施磷量为0.46 g/盆、分蘖末期土壤含水率占饱和含水率的75.2%;此参数在2012年度试验中对应实际产量达74.78 g/盆,与网络预测值相差为1.68%。
(2)为提高寒地黑土区水稻的产量,快速、准确的选择最优水肥组合,本文在饱和设计的基础上,提出了基于RAGA-BP神经网络模型对产量进行预测的方法,在2011年试验的基础上于2012年重新进行了试验,并对试验结果在同等条件下进行了验证,误差仅为1.68%。结果表明,运用饱和设计与RAGA-BP神经网络模型能较好的反映出产量与水肥施入量之间的复杂非线性关系,对指导农业生产试验具有一定的参考意义。
[1] Gan Y T,Lafond G P,May W E. Grain yield and water use relative performance of winter v s. spring cereals in east-central Saskatchewan[J].Canadian Journal of Plant Science,2000,80:533-541.
[2] 王小彬,高绪科,蔡典雄.旱地农田水肥相互作用的研究[J].干旱地区农业研究,1993,11(3):6-11.
[3] Karasov V G,Irrigation efficiency in water delivery[J].Technology,1982,2:62-74.
[4] Terry A Howell.Enhancing water use efficiency in irrigated agriculture[J].Agronomy Journal,2000,2:690-697.
[5] 文宏达,刘玉柱,李晓丽,等.水肥耦合与旱地农业持续发展[J].土壤与环境,2002,11(3):315-318.
[6] 朱庆森,邱泽森,姜长鉴. 水稻各生育期不同土壤水势对产量的影响[J].中国农业科学,1994,27(6):15-22.
[7] 杨建昌,朱庆森,王志琴,等.不同土壤水分状况下氮素营养对水稻产量的影响及其生理机制的研究[J].中国农业科学,1995,29(4):58-66.
[8] 高 隽.人工神经网络原理及仿真实例[M].北京:机械工业出版社,2003.
[9] Holland J H.Genetic algorithms[M].Science American,1992.
[10] 金菊良,杨晓华,丁 晶.标准遗传算法的改进方案----加速遗传算法[J].系统工程理论与实践,2001,(4):8-13.
[11] 叶 咸,许 模,廖晓超,等.遗传算法优化BP神经网络在求解水文地质参数中的应用[J].水电能源科学,2013,31(12):55-58.
[12] 基于BP人工神经网络和改进遗传算法的钩藤碱的提取工艺优化研究[J].计算机与现代化,2012,(8):17-20.
[13] 徐仲儒.农业试验最优回归设计[M].哈尔滨:黑龙江科学技术出版社,1988.
[14] 魏永霞,何双红.控制灌溉条件下水肥耦合对水稻产量及其构成因子的影响[J].灌溉排水学报,2010,29(5):98-102.
[15] Matlab中文论坛.Matlab神经网络30个案例分析[M].北京:北京航空航天大学出版社,2010.
