基于气温预报和HS公式的不同生育期参考作物腾发量预报

常晓敏，高占义，王少丽，罗玉峰(1.中国水利水电科学研究院，北京 10008；2.国家节水灌溉北京工程技术研究中心，北京 100048；.武汉大学水资源与水电工程科学国家重点实验室，武汉 40072)

作物需水量是农业用水的主要组成部分，它的准确计算与预报是制定农作物灌溉制度的基础，也是促进农业节水的关键[1]。而参考作物腾发量ET0是估算作物需水量的基础[2,3]，也是灌溉预报和灌溉决策的基础，准确的ET0计算和预报可有效提高灌溉预报的精度和灌区水分利用效率[4-6]。关于参考作物腾发量ET0估算及预报的研究已有很多年的历史，但多是采用历史时间序列分析法进行ET0的估算及预报[7,8]，根据历史ET0变化过程预测未来的ET0。随着ET0估算及预报研究的深入以及天气预报准确度的提高，天气预报信息逐渐被应用于ET0预报研究中，并取得一定的研究成果[9-11]。

影响参考作物腾发量ET0的气象因素有很多，其中日照及温度被认为是最主要的影响因素[12]，罗玉峰[13]等分析了不同气候区气象因素对高邮灌区水稻作物需水量的影响，认为ET0随气温上升和相对湿度下降而呈显著上升趋势。周迎平[14]等分析了河南12个站点1971-2010年气候变化对主要作物需水量的影响，得出河南省作物需水量在6月达到最高值，在11或12月降低至最低值。曹红霞[15]等利用关中地区1961-2001年数据探讨了冬小麦和夏玉米需水量与相应生育期内气候因子的变化趋势。同一作物不同气候区或同一气候区作物不同生育期，太阳辐射、气温等气象条件有所不同，对参考作物腾发量ET0的影响也有所不同，关于不同地区参考作物腾发量计算与预报的研究有很多。FAO推荐的Penman-Monteith(PM)公式作为计算ET0的基本方法，有着较高的计算精度，但不足之处在于需要的基础气象数据较多，这给气象数据缺测地区ET0的计算及预报带来较大的局限性。

本文以南京站水稻和冬小麦为例，采用预见期1～7 d的气温预报数据和Hargreaves-Samani(HS)公式对水稻、冬小麦不同生育期内未来短期的ET0进行预报，并评价其预报效果，为灌区农业用水管理提供相对可靠的数据支撑，进而为针对灌区不同种植结构而提出的灌溉计划及灌溉管理提供参考依据。

1 数据来源与方法

1.1 数据来源

从“中国天气网”(http:∥www.weather.com.cn)收集了南京站2001-2015年逐日气象数据和2012年5月24日到2015年6月3日未来7 d气象预报数据。南京站位于北纬32°00′、东经118°48′，海拔7.1 m。历史气象数据包括最高气温、最低气温、平均气温、相对湿度、平均风速和日照时数，天气预报数据包括最高最低气温。

1.2 参考作物腾发量ET0预报

由于太阳辐射Ra只与纬度有关，1985年Hargreaves提出了仅需要基于气温数据的参考作物腾发量Hargreaves-Samani计算公式(以下简称HS法)，HS表达式如下[16]：

(1)

式中：ET0,HS为通过HS公式计算的ET0值，mm/d；C、E为公式的2个参数，其建议值分别为0.002 3、0.5[16]；Ra为太阳辐射，可根据日序数及站点的地理纬度计算，MJ/(m2·d)；λ为平均气温的蒸发潜热，通常取值为2.45，MJ/kg；Tmax、Tmin分别为最高最低气温，℃。

式(1)对不同类型气候区域均具有一定的合理性，但一些研究指出参数C、E具有地区变异性，可将HS公式中的2个参数C、E作地区校正，以提高公式的计算精度[17]，其中Ra计算公式为：

Ra=37.6dr(Wssinψsinδ+cosψcosδsinWs)

(2)

式中：J为日序数；δ为日倾角，rad；ψ为地理纬度，rad；Ws为日落角，rad；dr为日地相对距离。

Penman-Monteith公式[18](以下简称PM法)被FAO认为是用于计算参考作物腾发量ET0的首选方法，且计算精度较高，本文将该公式计算的ET0值作为基准值来校正HS公式的参数，其计算公式如下：

(3)

式中：ET0为参考作物腾发量，mm/d；Δ为温度～饱和水汽压关系曲线在T处的切线斜率，kPa/℃；T为平均气温，℃；ea和ed分别为饱和水汽压和为实际水汽压，kPa；Rn为净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；γ为湿度计常数，kPa/℃；U2为2 m高度处的风速，m/s。

首先，以南京站2001-2011年最高气温、最低气温、平均气温、相对湿度、平均风速、日照时数为输入，采用PM法计算的ET0值作为基准值，以气温数据(最高、最低气温)为输入，采用最小二乘法，确定HS公式中的2个参数C、E(表1所示)其次，以南京2012年6月-2015年6月天气预报中的最高最低气温数据为输入，代入校正后的HS公式即可得到水稻、冬小麦不同生育期ET0预报值，其中，南京水稻、冬小麦作物生育期划分如表1所示。

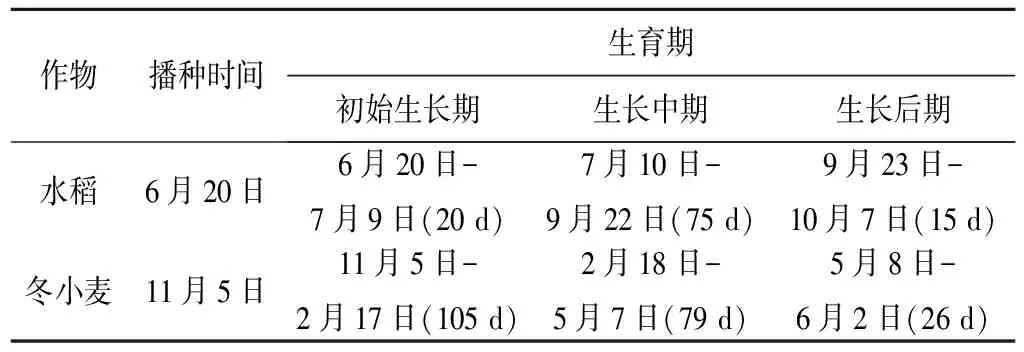
表1 南京水稻、冬小麦作物生育期划分Tab.1 Division of the growth period of rice and winter wheat in Nanjing

1.3 HS法预报精度评价指标

采用统计指标评价气温预报精度及基于气温预报数据和校正后HS公式的作物不同生育期ET0预报精度。统计指标包括平均绝对误差(MAE)、均方根误差(RMSE)、相关系数(r)。对于作物不同生育期气温预报和ET0，除上述5个指标外，另外还采用准确率进行评价。定义最高和最低气温预报值绝对误差在±1.5 ℃以内的天数占总样本个数的百分比为气温预报的准确率，类似地，定义ET0预报绝对误差在±1.5 mm/d的天数占总样本个数的百分比为ET0预报的准确率，其他各统计指标的计算公式如下：

(5)

(6)

式中：Pi为气温预报值或ET0,HS预报值；Oi为气温实测值或ET0,PM计算值；P、O分别为预报值和计算值的均值；i为预报样本序数，i=1,2,…；n为预报值的样本数。

2 结果与讨论

2.1 气温预报精度评价

表2为气温预报精度评价统计指标，最低、最高气温预报值和实测值相关系数高达0.98和0.94，说明最低和最高气温预报值和实测值存在紧密的相关关系。同时可看出，随着预见期的增加，最低、最高气温预报精度呈逐渐降低的趋势，且最低气温比最高气温的预报精度要高。但就整体来说，南京站天气预报中最低、最高气温预报精度尚可，也与其他人的研究类似[19]。

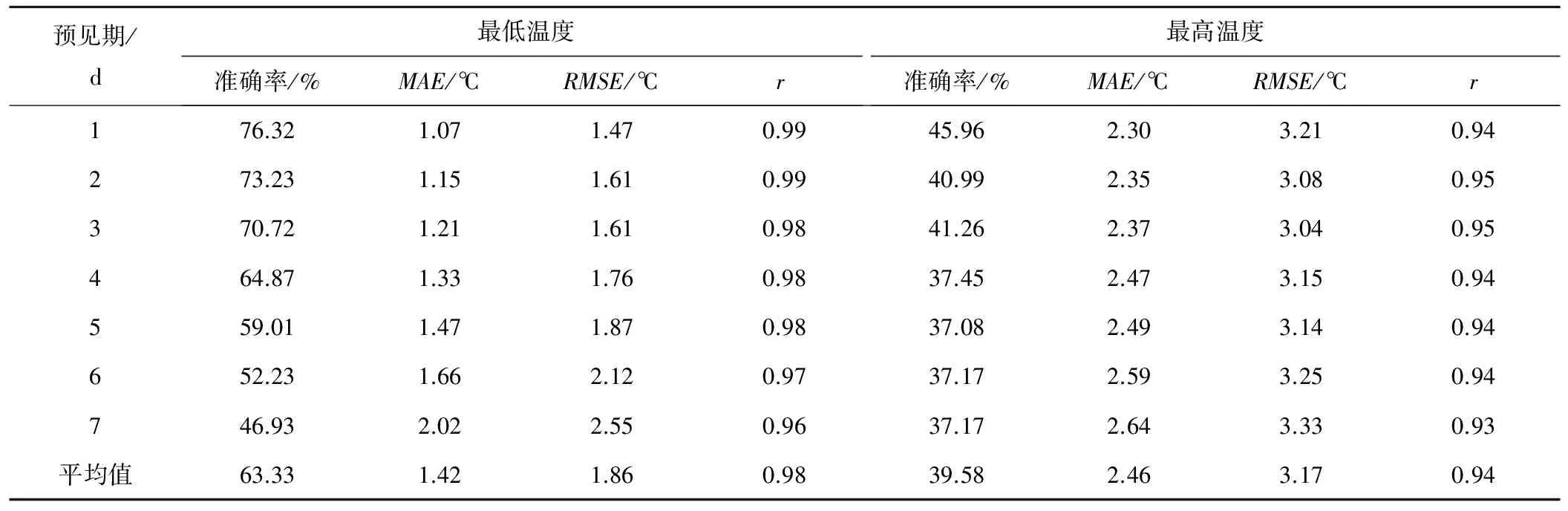
表2 气温预报精度评价指标值Tab.2 Indicator for evaluating accuracy in temperature forecast

2.2 作物不同生育期ET0预报敏感性分析

采用气温预报数据和Hargreaves-Samani(HS)公式预报作物不同生育期预见期1～7 d的参考作物腾发量ET0。气温预报数据作为唯一的输入变量直接影响着ET0的预报结果，为了更深入的了解气温预报误差对ET0预报误差的敏感性，采用单因子法进行敏感性分析，分别以水稻、冬小麦不同生育期的最高或最低气温平均值作为基准值，当最高或最低气温预报误差从-4 ～4 ℃范围内变动时，计算对应的ET0预报误差值，进而分析最高最低气温预报误差对ET0预报误差的影响程度。

图1为基于气温预报误差的作物不同生育期ET0预报误差敏感性分析，由图1可知，水稻不同生育期受最低、最高气温预报误差的影响程度分别为初始生长期>生长中期>生长后期，而冬小麦为生长后期>生长中期>初始生长期，由前面表2知，随着预见期的增加，气温预报误差逐渐增加，基于气温预报的ET0预报误差也呈逐渐增加的趋势，说明气温预报的准确程度直接影响着ET0的预报精度。同时也可以看出，相同生育期内水稻、冬小麦ET0预报误差对最高气温预报误差比最低气温预报误差更为敏感。同一生育期，相同的最低、最高气温预报误差对水稻ET0预报的影响程度大于冬小麦。

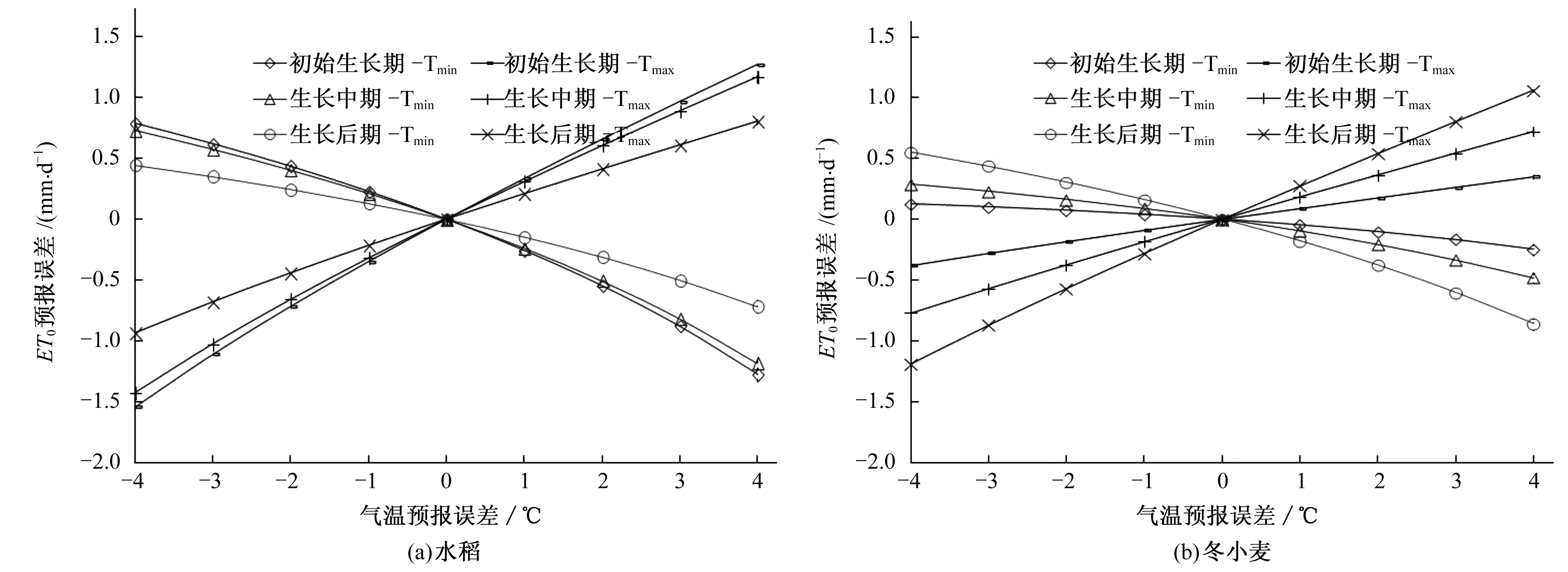
图1 基于气温预报误差的不同生育期ET0预报误差单因素敏感性分析Fig.1 Univariate sensitivity analysis of crop growth period ET0 forecast errors to temperatures forecast error

2.3 作物不同生育期ET0预报精度评价

基于气温数据的Hargreaves-Samani公式对不同类型气候区均具有一定的合理性，将HS公式中的2个参数C、E作地区校正后，可提高公式的计算精度，南京站基于气温数据的Hargreaves-Samani公式参数C、E校正数据分别为0.002 3和0.407 2。

图2为2012-2015年水稻、冬小麦不同生育期预见期为1、4和7 d的ET0预报值与ET0,PM计算值比较。尽管一些ET0预报值高于或低于ET0,PM计算值，但整体上预见期1～7 d内，水稻、冬小麦ET0预报值和ET0,PM计算值变化趋势较为一致，其中冬小麦ET0预报值与ET0,PM计算值接近程度更好，这可能是由于HS公式只考虑了温度对ET0的影响，而没考虑风速和湿度的影响以致产生较大的误差，水稻整个生育期处于6月中旬到10月中旬，此时期受季风影响较大，而冬小麦生育期处于11月初到次年的6月初，受季风影响较小。

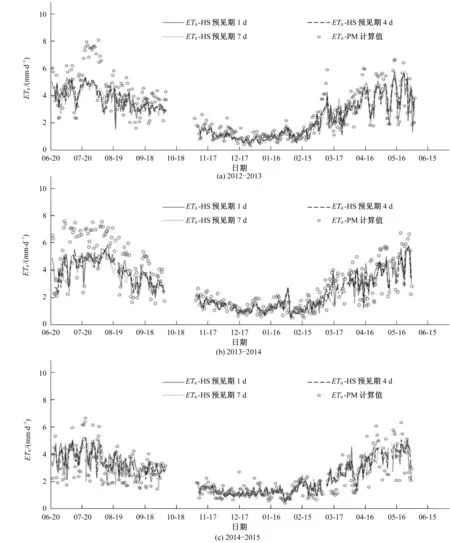
图2 水稻、冬小麦不同生育期ET0，HS预报值与ET0，PM计算值比较Fig.2 Comparisons of forecasted ET0，HS and calculated ET0，PM in different growth period of rice and winter wheat

同时可以看出，水稻的ET0预报值与ET0,PM计算值呈先增大后减小的趋势，参考作物腾发量最大值发生在分蘖期，这与气象因素及水稻的生长特性有很大关系，随着生育期的推进，太阳辐射减小，气温降低，参考作物腾发量呈缓慢下降趋势。而冬小麦生长期阴雨较多，光照少，气温低，大气蒸发能力小，因而需水量较小。从播种到拔节期，冬小麦幼苗生长缓慢，且气温较低，蒸发蒸腾能力较弱，ET0计算值和预报值均低于2 mm/d，初始生长期冬小麦ET0计算值和预报值呈缓慢下降趋势，这是因为越冬期太阳辐射减小、大气温度逐渐降低导致参考作物腾发量相应降低，这个时期冬小麦生长环境气温全年最低、生长缓慢，参考作物腾发量降到了全生育期最低，进入拔节期，太阳辐射与大气温度迅速增加，蒸发蒸腾速率逐渐增大，参考作物腾发量呈上升趋势，之后，随着生育期的推进，进入拔节孕穗期后ET0计算值和预报值上升趋势变缓，这可能是由于成熟期植株的衰老使冬小麦蒸发蒸腾能力下降，这与作物生育期所处的气候条件和作物的生理特性都有很大的关系。

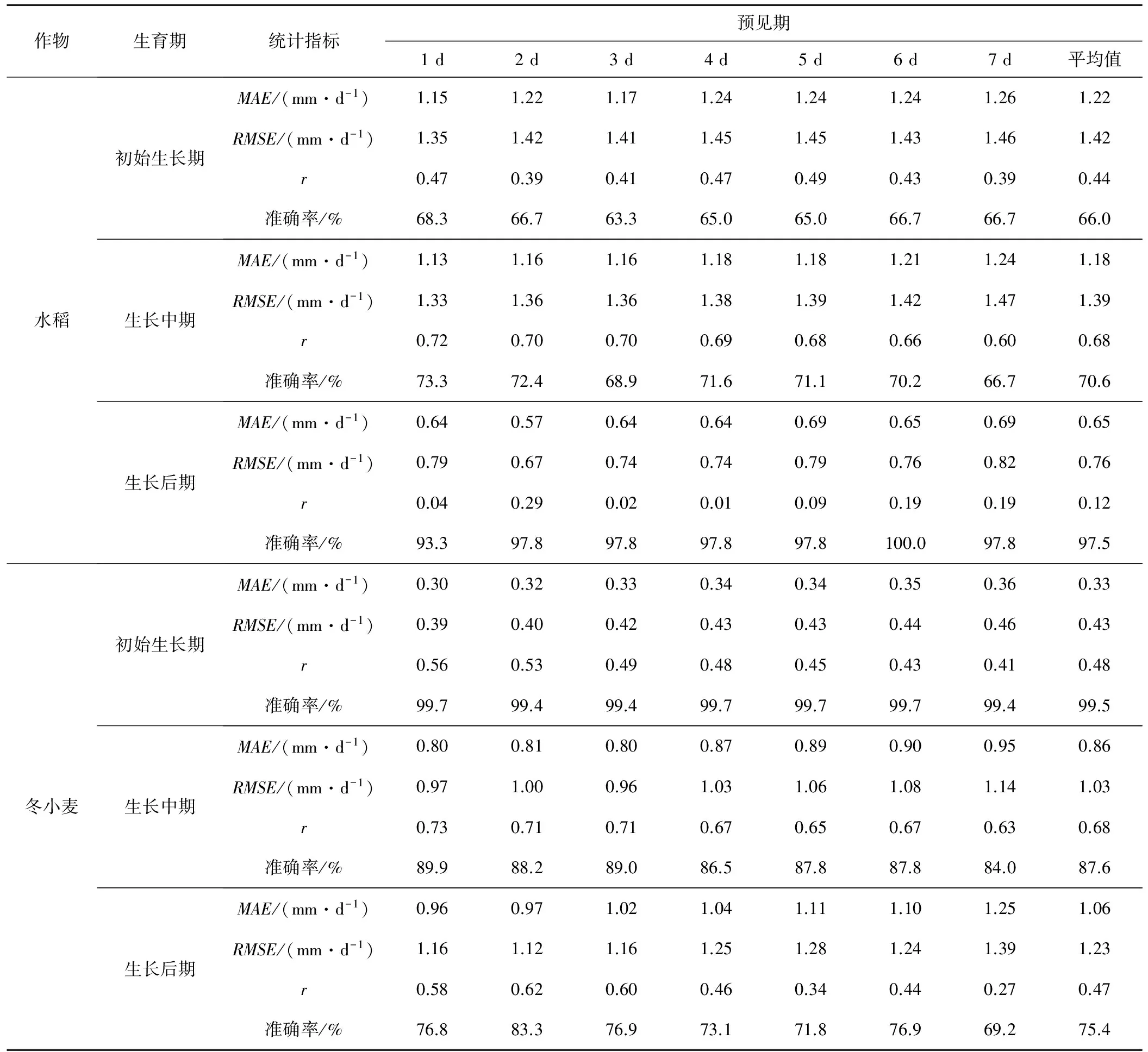
表3 水稻、冬小麦ET0预报精度统计评价Tab.3 Statistical evaluation of accuracy in ET0 forecast of rice and winter wheat

表3为水稻、冬小麦不同生育期ET0预报值和PM法计算值统计比较。从表3中可以看出，随着预见期的增大，ET0预报精度呈下降趋势，这是因为随着预见期的增加，气温预报误差逐渐增大。水稻不同生育期ET0预报精度生长后期>生长中期>初始生长期，而冬小麦不同生育期ET0预报精度初始生长期>生长中期>生长后期，因为ET0预报敏感性分析中得出水稻不同生育期受气温预报误差的影响程度分别为初始生长期>生长中期>生长后期，而冬小麦为生长后期>生长中期>初始生长期，生育期各阶段对气温预报误差越敏感，对应的ET0预报精度越低。水稻生育期平均准确率为66.0%～97.5%，MAE为0.65～1.22 mm/d，RMSE为0.76～1.42 mm/d，冬小麦生育期平均准确率为75.4%～99.5%，MAE为0.33～1.06 mm/d，RMSE为0.43～1.23 mm/d，由于生育期各阶段时间较短，相关系数计算效果不好，但通过对整个生育期数据分析，全生育期水稻和冬小麦相关系数计算效果较好，分别可达到0.60和0.80左右。

3 结 语

本文以南京为例，采用气温预报数据和Hargreaves-Samani(HS)公式对水稻、冬小麦不同生育期内预见期为1～7 d的参考作物腾发量ET0进行预报，并与采用实测气象数据和PM法计算的ET0值进行比较，得出的主要结论如下。

(1)采用基于气温的Hargreaves-Samani(HS)公式短期预报水稻和冬小麦不同生育期参考作物腾发量ET0，效果较好，预见期1～7 d的气温预报及ET0预报精度也达到一定的可利用程度，但随着预见期的增加，气温预报准确率逐渐降低，ET0预报精度也呈下降趋势。

(2)作物生育期各阶段对气温预报误差越敏感，ET0预报精度越低，水稻不同生育期的ET0预报误差受气温预报误差的影响程度分别为初始生长期>生长中期>生长后期，而冬小麦为生长后期>生长中期>初始生长期，相应的，水稻不同生育期ET0预报精度生长后期>生长中期>初始生长期，而冬小麦不同生育期ET0预报精度初始生长期>生长中期>生长后期。

(3)从整个生育期看，冬小麦ET0预报精度较水稻效果更好，这主要是由于水稻整个生育期处于季风时期，受风速和湿度的影响较大。

[1] 温随群, 杨秋红, 潘 乐, 等. 作物需水量计算方法研究[J]. 安徽农业科学, 2009,(2):442-443.

[2] Li Y H, Cui Y L. Real-time forecasting of irrigation water requirements of paddy fields[J]. Agricultural Water Management, 1996,31(3):185-193.

[3] 廖轶群, 李 毅, Horton R, 等. 新疆参考作物腾发量多元回归模型及空间分布[J]. 排灌机械工程学报, 2012,30(1):117-124.

[4] Todorovic M, Karic B, Pereira L S. Reference evapotranspiration estimate with limited weather data across a range of Mediterranean climates[J]. Journal of Hydrology, 2013,481(8):166-176.

[5] Cai J, Liu Y, Lei T, et al. Estimating reference evapotranspiration with the FAO Penman-Monteith equation using daily weather forecast messages[J]. Agricultural & Forest Meteorology, 2007,145(1-2):22-35.

[6] 蔡甲冰, 刘 钰, 雷廷武, 等. 应用自适应神经模糊推理系统(ANFIS)的ET0预测[J]. 农业工程学报, 2004,20(4):13-16.

[8] 罗玉峰, 崔远来, 蔡学良. 参考作物腾发量预报的傅立叶级数模型[J]. 武汉大学学报:工学版, 2005,38(6):45-47.

[9] Luo Y, Chang X, Peng S, et al. Short-term forecasting of daily reference evapotranspiration using the Hargreaves-Samani model and temperature forecasts[J]. Agricultural Water Management, 2014,136(2):42-51.

[10] 迟道才, 王晓瑜, 周 彬, 等. 基于天气预报改进模型ET0实时预报应用[J]. 人民长江, 2008,39(8):5-6.

[11] Ballesteros R, Ortega J F, Moreno M. FORETo: New software for reference evapotranspiration forecasting[J]. Respiration, 2015,89(1):12-14.

[12] 李 禄, 迟道才, 刘 丽, 等. 太子河流域参考作物腾发量变化特征及影响因素分析[J]. 沈阳农业大学学报, 2007, 38(3): 387-390.

[13] 罗玉峰, 彭世彰, 王卫光, 等. 气候变化对水稻灌溉需水量的影响——以高邮灌区为例[J]. 武汉大学学报:工学版, 2009, 42(5): 609-613.

[14] 周迎平, 胡正华, 崔海羚, 等. 1971-2010年气候变化对河南省主要作物需水量的影响[J]. 南京信息工程大学学报:自然科学版, 2013,(6):515-521.

[15] 曹红霞, 粟晓玲, 康绍忠, 等. 关中地区气候变化对主要作物需水量影响的研究[J]. 灌溉排水学报, 2008,27(4):6-9.

[16] Hargreaves G H, Allen R G. History and evaluation of Hargreaves evapotranspiration equation. J Irrig Drain Eng ASCE[J]. Journal of Irrigation & Drainage Engineering, 2003,129(1):187-188.

[17] 胡庆芳, 杨大文, 王银堂, 等. Hargreaves公式的全局校正及适用性评价[J]. 水科学进展, 2011,22(2):160-167.

[18] Allan R G, Pereira L S, Raes D, et al. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56[J]. FAO Irrigation & Drainage Paper, 1998,56.

[19] 李国翠, 连志鸾, 赵彦厂, 等. 石家庄温度预报检验及影响因子分析[J]. 气象与环境学报, 2009,25(1):15-18.