基于人工神经网络土壤墒情动态预测模型应用研究
2016-03-23侯晓丽冯跃华吴光辉何印兴常东明杨会明
侯晓丽,冯跃华,吴光辉,何印兴,常东明,杨会明
(1.河南省豫东水利工程管理局,河南 开封 475000;2.郑州大学,郑州 450001)
土壤墒情,通常指土壤是适合农作物生长的含水量情况,直接影响着作物的正常生长及其产量、产品的形成。快速、准确地测定农田土壤水分,探明作物生长发育期内土壤水分盈亏,做出节水灌溉、施肥决策或排水措施,对最终实现高产、高效、优质农业具有重要意义。我国水资源问题突出,节约用水是最有效最直接的方法,对土壤墒情进行实时监测和动态预报,就显得非常有必要。
杨绍辉、王一鸣等[1]以组件式GIS软件为开发平台,对土壤墒情进行实时监测,直观反映北京地区土壤墒情趋势。王婧雅、高学睿等[2]运用改进的克里金插值法对大尺度农田土壤墒情分布进行了插值,分析了区域大尺度土壤墒情的分布规律,并以邯郸市为例,验证了修正克里金插值法的可行性和可靠性。尚松浩[3]研究了土壤墒情确定性模型与随机性模型发展情况,论证了墒情预报对于水资源短缺条件下农田水分的合理调控的重要意义,预测了墒情预报模型的发展趋势。李彦彦、张金萍等[4]针对陆浑灌区极端天气频发的问题,采用小波分析对灌区降水量、平均气温及作物需水量进行多时间尺度周期分析,并且运用Mann-Kendall法对各气象要素进行突变检验。杨会明[5]构建了大型引黄灌区三义寨灌区土壤墒情动态预测模型,计算了作物灌溉需水量,并且计算了灌区引黄需水量。多年来土壤墒情预报主要依靠预报人员的经验,缺乏准确的、科学的预报模型,不能够对农作物节水灌溉提供可靠的参考依据。因此,我们需要基于所研究灌区自然条件特性,建立理论基础详实、结构形式简单、计算参数容易取得、模拟操作步骤相对简单的土壤墒情预报数学模型,快速准确预测农作物成长发育期间土壤含水量变化情况,为农作物节水灌溉工作提供科学依据。
本文在分析了三义寨灌区土壤墒情的时空分布规律的基础上,基于人工神经网络理论建立了不同埋深条件下的土壤墒情预报数学模型,实时预测灌区主要农作物生长期间的土壤含水量变化情况;该数学模型在三义寨灌区的成功应用表明,基于人工神经网络的墒情预报数学模型能够较好的预测土壤墒情变化情况,可为大型引黄灌区的土壤墒情预测提供参考依据。
1 人工神经网络的土壤墒情动态预测模型
BP神经网络是一种前向网络,在现阶段神经网络模型中得到了广泛的应用;BP神经网络模型一般由数据输入层、计算结果输出层和若干隐含层构成,不同构层之间的神经元通过权连接进行不同的数据交换。图1为人工神经网络结构模型的传递示意图;数据输入层、结果输出层和隐含参数层的神经元数目分别取为r、q、m,神经网络模型表示为BP(r,q,m),结构图中a1~an为输入层的各个分量,w1~wn表示模型中不同突触的权值,b表示模型的偏置情况;t表示模型的结果输出值,f表示模型计算过程的传递函数。一般的表示公式为t=f(WA′+b)。
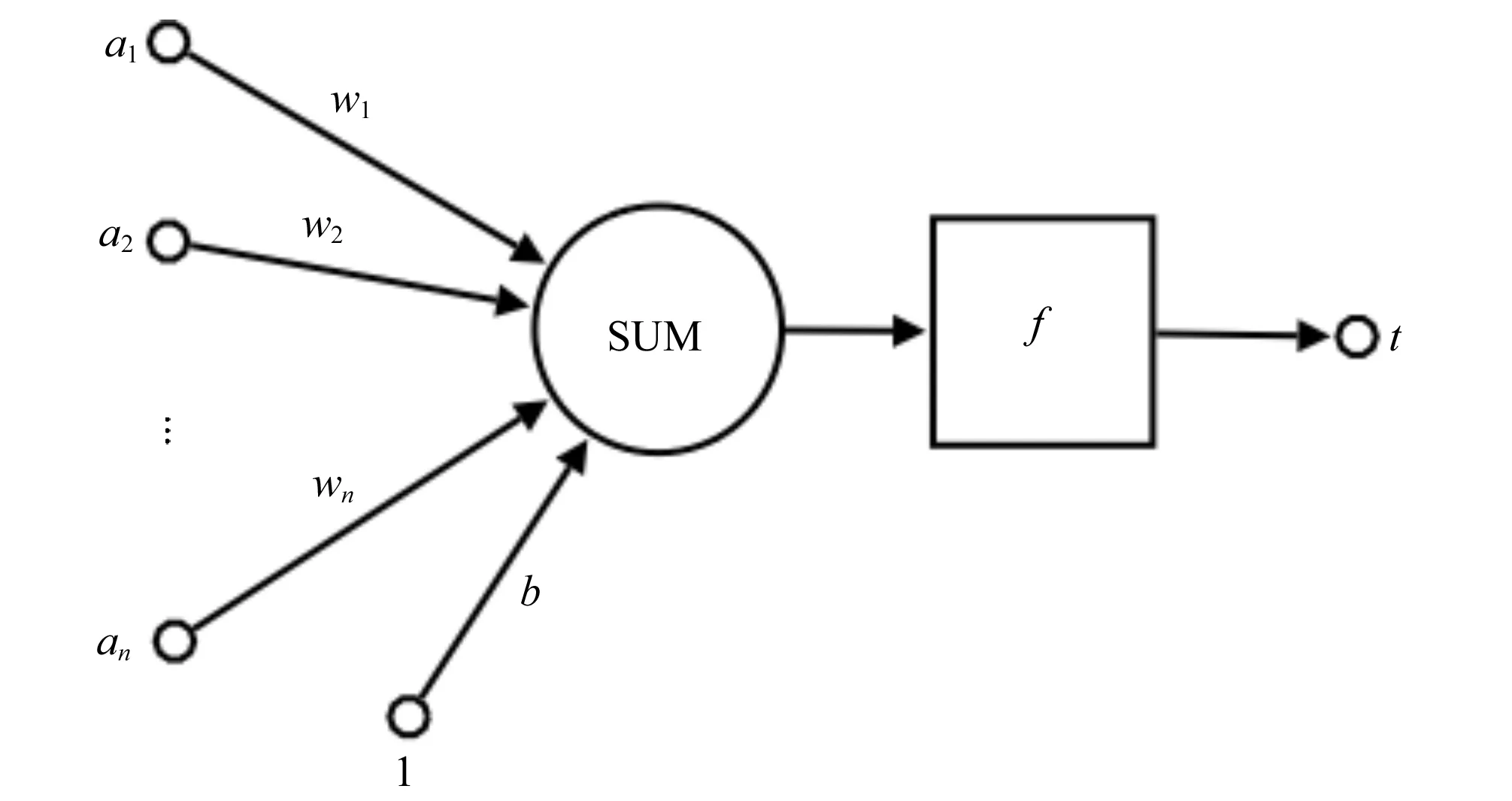
图1 人工神经网络结构模型传递示意图
神经元模型计算过程主要根据一个神经元输入向量和权向量的内积值,采用非线性函数进行传递计算,求得神经元的标量结果。单个神经元通过采用超平面方法把n维空间分成两个部分,进而判断给定的输入向量属于超平面的哪一侧。超平面方程一般可以表示为Wp+b=0,其中,W表示权向量,b为偏置,p为超平面上的向量。
2 模型数据来源及土壤墒情规律分析
2.1 数据来源
本文采用2011-2012年度三义寨灌区逐月旬的实测土壤墒情数据,具体分别为0.1、0.2和0.4 m土壤墒情分布情况,数据资料十分丰富,为人工神经网络的土壤墒情动态预测模型建立与预报提供了数据基础。
2.2 土壤墒情规律分析
(1)时间变化规律。通过对2011-2012年度逐月旬的土壤墒情实测数据统计分析可以看出,三义寨灌区土壤墒情整体变化趋势平稳,一般每年的8月份土壤墒情值达到最大。通过对比分析三义寨灌区多年土壤墒情数据的变化情况可以看出,该地区多年土壤墒情处于一个稳定变化范围,土壤墒情数据多年变化情况整体处于稳定水平,各不同埋深条件下实测数据之间存在一定的差值,一般表现为下层土壤墒情大于上层的土壤墒情,见图2。

图2 不同埋深条件下土壤墒情变化
(2)不同地区变化规律。灌区范围内(主要指河南的开封、商丘和山东的菏泽地区)10、20、40 cm埋深条件下土壤墒情变化趋势基本一致。由图3可以看出,宁陵、睢阳、睢县3个地区的土壤墒情变化情况最为接近,墒情数据大小基本一致,民权地区虽然墒情数据变化趋势基本一致,但墒情值相对较小,说了民权地区相对最容易发生土壤缺水的干旱情况。虞城地区的土壤墒情数据波动值明显大于其他地区,表明虞城地区土壤墒情影响因子与其他县区土壤墒情的影响因子存在明显不同。
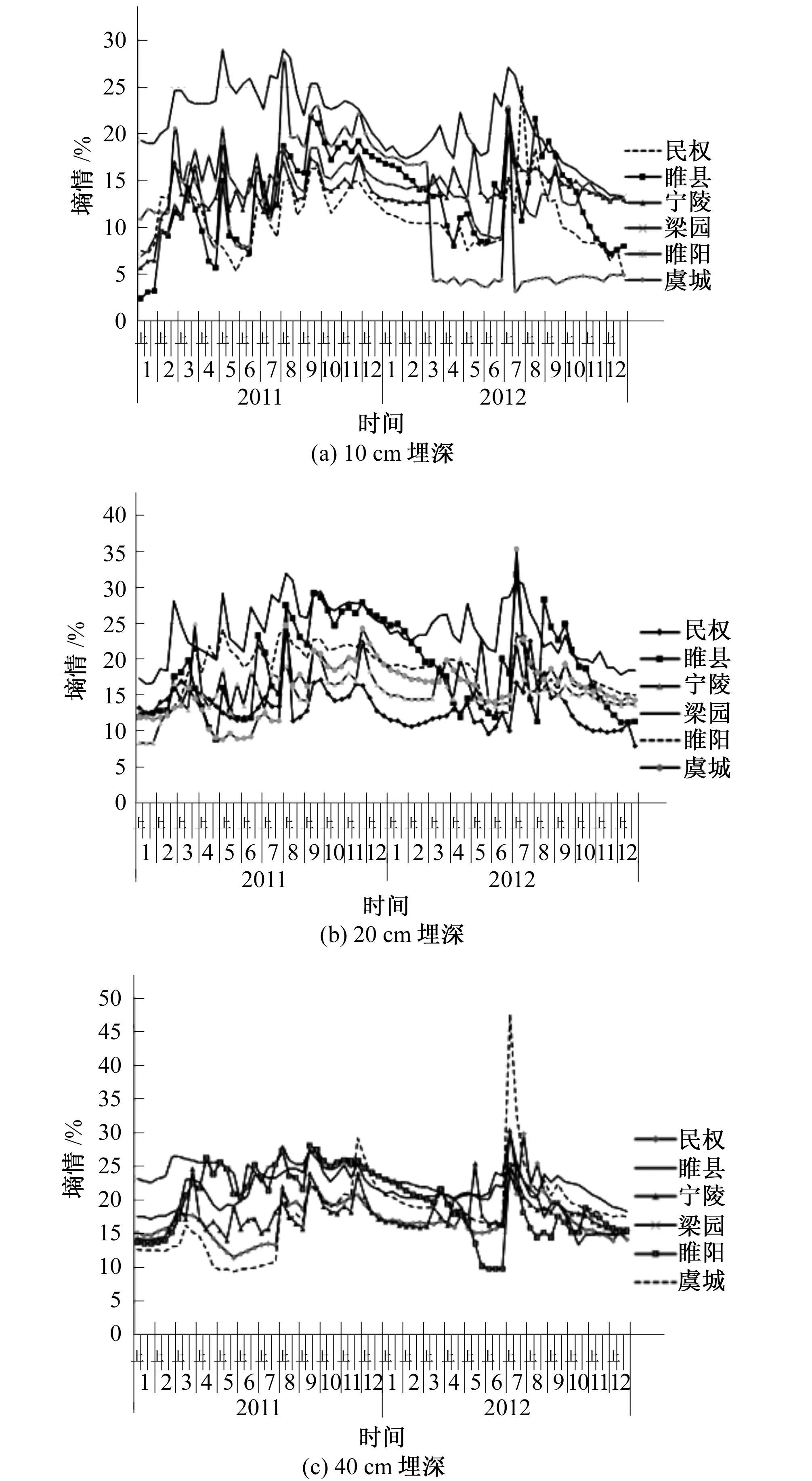
图3 各地区不同埋深条件下土壤墒情变化值
3 土壤墒情预测模型建立与检验
本文基于人工神经网络(ANN)理论构建立了三义寨灌区不同埋深条件下土壤墒情动态预测数学模型。模型输入变量主要为气温、风速、日照时长、湿度及降水量等,计算结果的输出值为不同埋深条件下的土壤墒情计算值。
模型输入条件采用三义寨灌区不同埋深条件下的实测土壤墒情数据,降水量为旬降水量之和,其他输入数据采用的是旬平均值。模型计算过程中共采用78组数据(2011年1月-2012年6月)进行模型的率定与验证。
根据人工神经网络预测模型的需要,利用极值归一方法对实测数据进行标准化处理,其中计算方法为yi=(xi-x最小)/(x最大-x最小)。在已经处理好的数据的基础上,分别建立了不同埋深条件下的人工神经网络动态预测数学模型(见表1)。
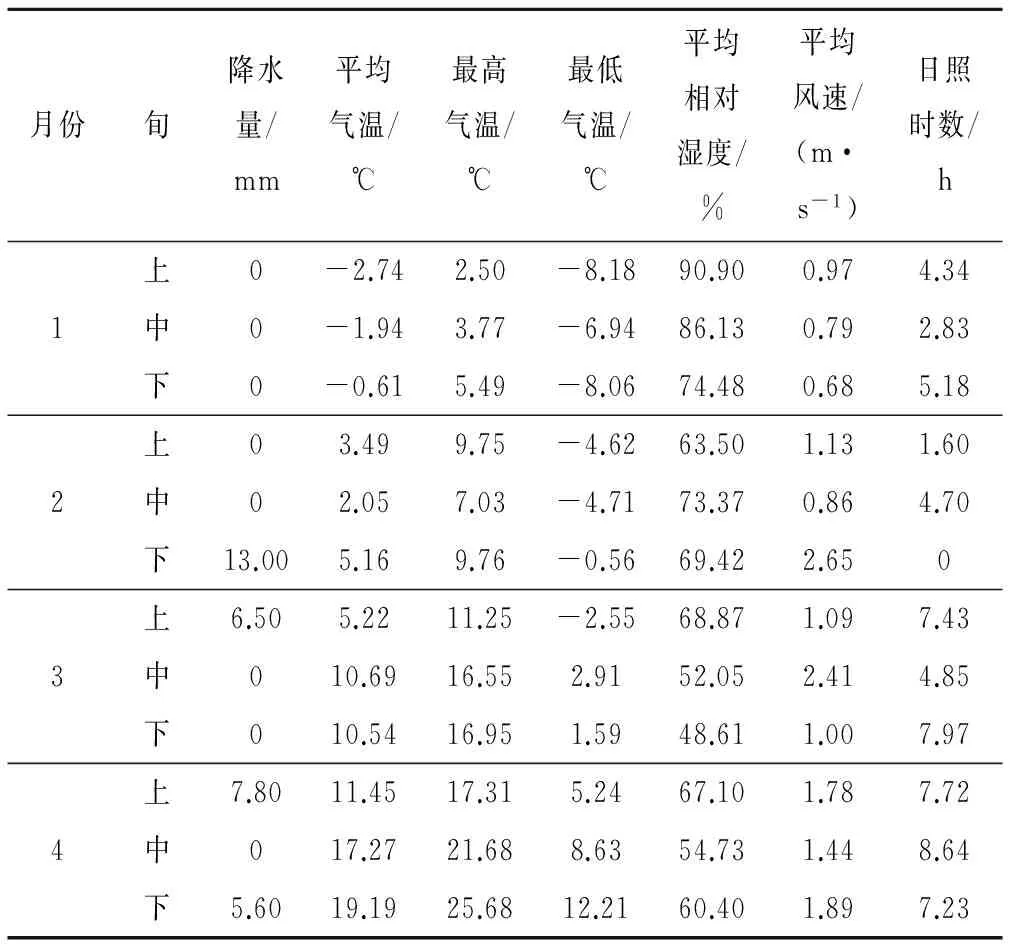
表1 2011年灌区主要气象资料
(1)40 cm埋深条件下土壤墒情预测。在构建40 cm埋深条件下土壤墒情动态预测模型时,模型选择为2层,选用恒等函数作为模型的输出函数,隐含层采用sigmoid函数;模型对输入数据采用批量处理方法,优化计算方法采用调整的共轭梯度,Lambda初始值为5×10-7,Sigma值初始值为5×10-5,间隔偏移范围为±0.5,选用已经建立好的人工神经网络模型对2012年7-12月实测土壤墒情进行模拟计算。
研究发现:40 cm埋深条件下墒情预测值为19.6,标准差为3.2,与实测值较为接近。通过spss相关分析可以看出,模型计算结果与实测数据吻合较好,模型计算值与实测数据的相关值大于0.95,协方差为11.2,具有较好的相关关系(0.01置信水平),该模型较好的预测三义寨灌区40 cm埋深条件下土壤墒情变化情况(见图4)。
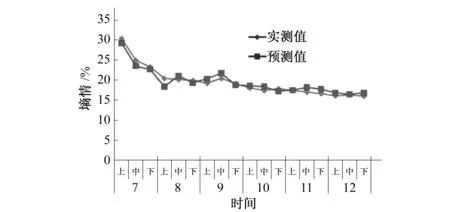
图4 40 cm埋深条件下土壤墒情变化对比图
(2)20 cm埋深条件下土壤墒情预测。在构建20 cm埋深条件下土壤墒情预测模型时,模型选择为2层,选择双曲正切函数作为模型的输出函数,隐含层采用sigmoid函数;模型对因变量进行了标准化的处理,修正值为0.02。输入数据采用批量处理方法,优化计算方法采用调整的共轭梯度,Lambda初始值为5×10-7,Sigma值初始值为5×10-5,间隔偏移幅度为±0.5,选用已经建立好的人工神经网络模型对2012年7-12月份实测土壤墒情进行计算分析。
研究发现,20 cm埋深条件下墒情预测值为17.9,标准差为3.3,通过spss相关分析发现,模型计算结果与实测数据吻合较好。进一步对比分析,模型计算值与实测数据的相关值为大于0.98,协方差为11.0,在0.01置信区间表现为明显的相关关系,该模型较好的预测三义寨灌区20 cm埋深条件下土壤墒情变化情况(见图5)。
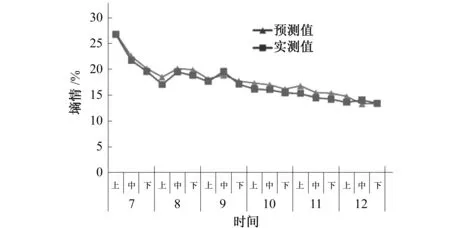
图5 20 cm埋深条件下土壤墒情变化对比图
(3)10 cm埋深条件下土壤墒情预测。模型对因变量进行了标准化的处理,修正值为0.02,对输入数据进行批量处理,采用调整的共轭梯度对计算方法进行优化处理,Lambda初始值为5×10-7,Sigma值初始值为5×10-5,间隔偏移幅度为±0.5。
研究发现:10 cm埋深条件下墒情预测值为14.3,标准差为3.1。通过spss相关分析可以看出,模型计算结果与实测数据吻合较好,模型计算值与实测数据的相关值为大于0.97,协方差为8.6,在0.01置信区间表现为明显的相关关系,该模型较好的预测三义寨灌区10 cm埋深条件下土壤墒情变化情况(见图6)。
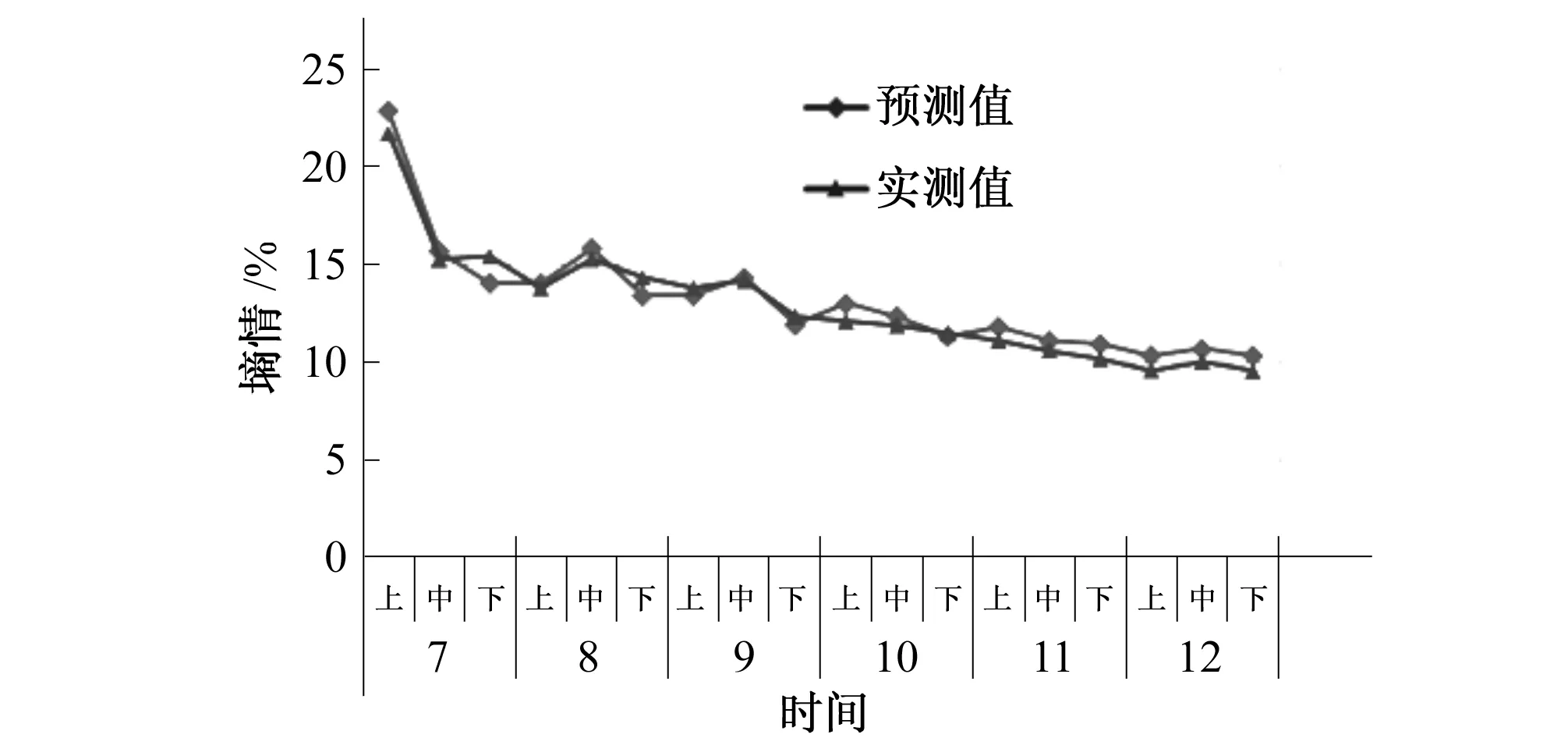
图6 10 cm埋深墒情预测值与实测值对比图
4 结 语
(1)利用2011-2012年度实测数据资料,分析了三义寨灌区墒情分布规律,年内墒情总体趋势平稳,一般情况下每年8月份墒情达到最大值;多年来土壤墒情整体趋势相对较为平稳,处于一个稳定的水平;不同埋深条件下土壤墒情存在明显的差别,一般表现为下层土壤墒情大于上层的土壤墒情。
(2)基于人工神经网络(ANN)理论建立了的不同埋深条件下三义寨灌区土壤墒情预测数学模型。以灌区0.1、0.2和0.4 m 3层土壤观测实际资料对模型进行检验,计算值与实测数据吻合较好,模型具有较强的实用性,可用于了三义寨灌区不同埋深条件下的土壤墒情模拟计算与预测。
(3)基于人工神经网络(ANN)理论的土壤墒情数值预报数学模型在三义寨灌区的成功应用,为大型灌区精细化、准确化灌溉提供了先进的计算机支撑技术和手段,有利于对大型灌区进行更好的实时管理。
[1] 杨绍辉,王一鸣,孙 凯. 土壤墒情(旱情)监测与预测预报系统的设计与开发[J].中国农业大学学报,2007,12(4):75-79.
[2] 王婧雅,高学睿,陆垂裕. 修正克里金插值法在大尺度农田土壤墒情插值中的应用[J].中国农业大学学报,2013,31(3):116-119.
[3] 尚松浩. 土壤水分模拟与墒情预报模型研究进展[J]. 沈阳农业大学学报, 2004, 5(5-6):455-458.
[4] 李彦彦,张金萍,林小敏. 陆浑灌区主要气象因素与作物需水量的演变特征分析[J].水电能源科学,2015,33(10):28-32.
[5] 杨会明. 三义寨灌区土壤墒情动态预测及引黄用水需求研究[D]. 郑州:郑州大学, 2014.
[6] 程殿龙,马宏志,许晓春.神经网络方法在土壤墒情预测中的应用[J].中国农村水利水电, 2002,(7):6-8.
[7] 魏占民,陈亚新,史海滨, 等. BP 神经网络的春小麦作物水模型的初步研究[J].灌溉排水,2002,21(2):12-16.
