水文序列延长后已建水库防洪特征水位复核

周研来，陈 进，许继军

（1．长江科学院a．水资源综合利用研究所；b．流域水资源与生态环境科学湖北省重点实验室，武汉 430010；2．武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）



水文序列延长后已建水库防洪特征水位复核

周研来1a，1b，2，陈 进1a，1b，许继军1a，1b

（1．长江科学院a．水资源综合利用研究所；b．流域水资源与生态环境科学湖北省重点实验室，武汉 430010；2．武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

摘 要：为探究洪水不确定性对大坝防洪特征水位设计的影响，采用水库调洪演算的随机微分方程推求防洪特征水位的概率分布线型，以三峡水库为例，通过调洪演算将洪水不确定性转换为防洪特征水位的不确定性，以分析已建水库防洪特征水位的分布规律，并对三峡水库防洪特征水位进行了复核分析。研究结果表明：随着样本容量的增加，洪水的信息量增大，三峡大坝设计资料和原校核洪水位（180．4 m）的可靠度均有所提高；当样本容量为120 a时，设计洪水资料和原校核洪水位的可靠度分别为93．19%和99．17%。研究结果为提高水库大坝安全设计提供了理论依据。

关键词：水文序列；防洪特征水位；不确定性；随机微分方程；特征水位复核；三峡水库

1 研究背景

大坝防洪特征水位设计是在拟定泄洪建筑物及已确定防洪限制水位的条件下，用给出的设计洪水过程、泄洪建筑物的泄洪能力曲线及库容曲线等基本资料，按照规定的防洪调度规则，推求相应的最高调洪水位。对于承担下游防洪任务的大坝而言，其防洪特征水位通常包括防洪高水位、设计洪水位和校核洪水位。因调洪演算过程中随机因素的客观存在，导致大坝防洪特征水位为随机变量（上游水库群建成后，随机性会降低）。影响防洪特征水位分布的不确定性因素包括水文不确定性、水力不确定性和库容水位关系不确定性等［1］。其中主要影响因素为水文不确定性，它又包括洪水不确定性［1－4］和水文预报不确定性［5］。现有大坝防洪特征水位复核常采用典型年法和随机模拟法［1－5］，且国内众多水库设计之初所用水文序列较短，随着建成运行后，水文资料不断积累，水文序列不断延长，特别是水库建成后发生过较大洪水的水库，有必要开展设计洪水及防洪特征参数的复核工作。本次重点探讨洪水不确定性对大坝防洪特征水位设计的影响。此外，采用水库调洪演算的随机微分方程推求防洪特征水位的概率分布型状，通过调洪演算将洪水不确定性转换为防洪特征水位的不确定性，以分析大坝防洪特征水位的分布规律，并对大坝防洪特征水位进行复核。本文以三峡大坝为例，探讨了该方法的适用性和合理性。

2 防洪特征水位的复核分析

2．1 库水位分布规律分析

在调洪演算过程中库水位H（t）由于受多种随机因素的影响，导致H（t）是一个平稳独立增量过程，并且符合Wiener过程定义的随机过程，即库容水位H（t）满足随机微分方程［3］）式（1）。

式中：μQ(t )和μq(H，t )分别为当前时段内的平均入库流量和平均出库流量；t0为水库起调时刻；H0为起调水位，本文取汛限水位；G( H )＝dV( H )／dH，V( H )是库水位H对应水库库容；B（t）是均值为0 的Wiener过程。

对于本文而言，仅考虑坝址洪水的不确定性时，其大小只与坝址洪水过程的方差σ2Q（t）有关，即有σ2H（t）＝σ2Q（t）t／G2（H）［5］。根据Wiener过程的性质可知，库水位H（t）服从均值为（（μQ（t）－μq（H，t））／G（H））t和方差为σ2Q（t）t／G2（H）的正态分布，即H（t）～N（（（μQ（t）－μq（H，t））／G（H））t，σ2Q（t）t／G2（H））。

2．2 防洪特征水位抽样误差分析

按年最大洪水过程调洪演算得到库水位过程H（t），统计出调洪最高水位max{ H( t ) }作为大坝防洪特征水位序列Yf。因库水位过程H（t）为独立同分布的正态分布，则Yf也近似服从正态分布。假设大坝防洪特征水位序列Yf服从均值为μ、方差为σ2的正态分布，则有

正态分布参数μ和σ2的极大似然估计值和分别为：

式中：yi为抽自式（2）的样本；n为样本容量；为样本均值；S2为样本方差。

假设Y为抽自总体N( μ，σ2)的一个样本，且该样本不参与样本参数和S2的估计。通过样本均值和样本标准差得到防洪特征水位样本序列标准化的计算公式，即

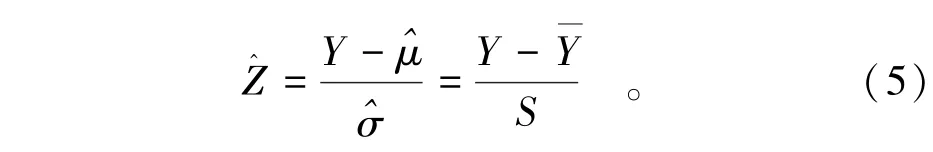
通过总体均值和总体标准差得到防洪特征水位样本序列Z标准化的计算公式，即

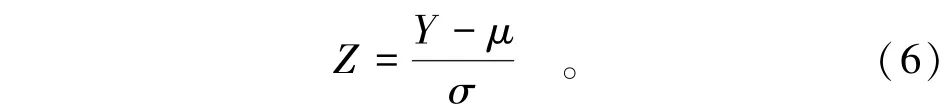
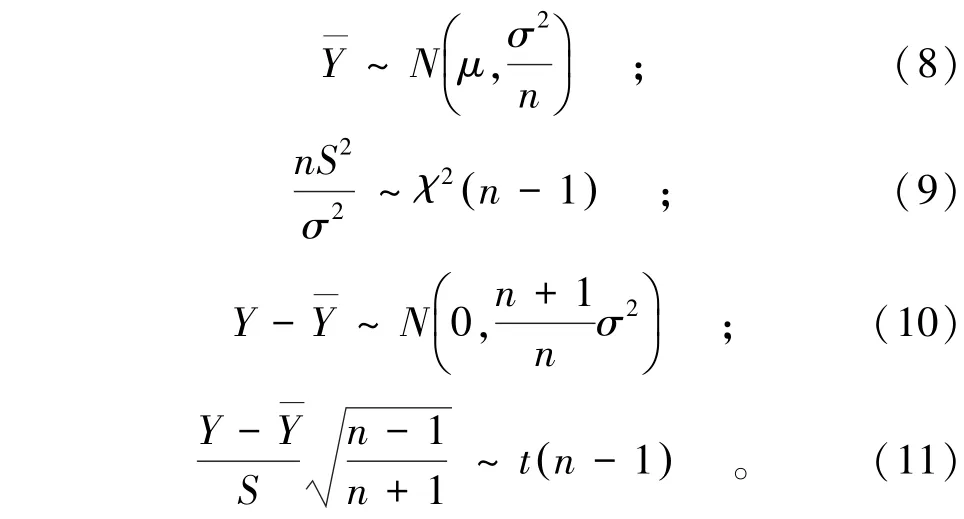
根据式（7）和式（11）可知，推求随机变量D的分布规律并非易事，因为它反映的是2个具有相关性随机变量Z和的差异性，一个随机变量服从标准正态分布，另一个随机变量服从学生t分布。尽管如此，也可通过随机变量D的数学偏差（Bias）和均方误差（Mean Squared Error，MSE）等统计指标来反映防洪特征水位序列的样本差异性［7］，即：

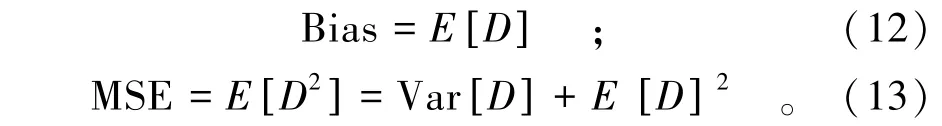
在工程实践中更偏爱于采用均方根误差（Root Mean Squared Error，RMSE）来替代MSE，即

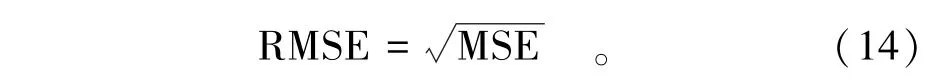
Bias的计算式为

将式（15）代入式（13）可得

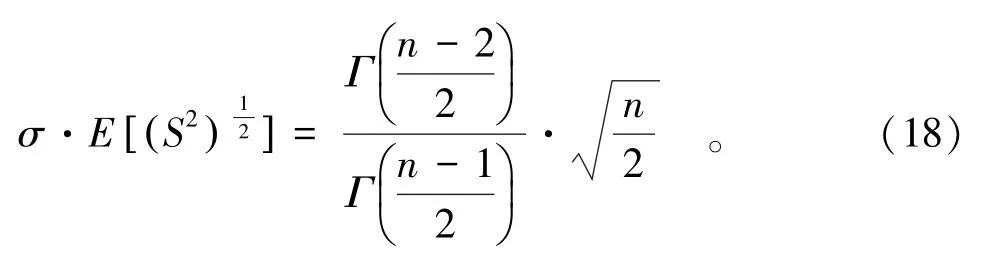
将式（18）代入式（16），可得［7］

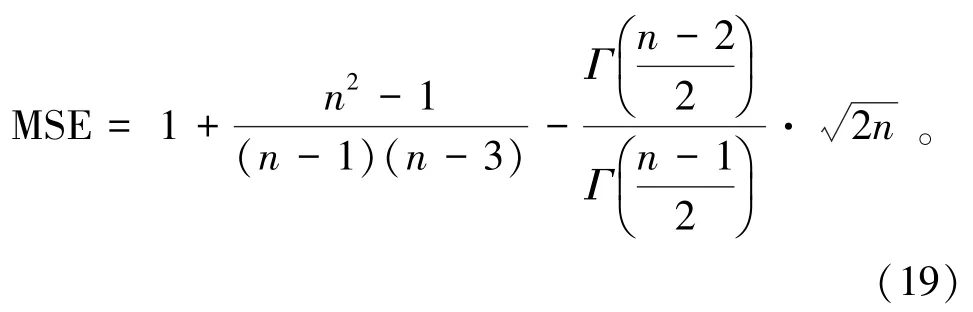
将式（19）代入式（14），可得［7］

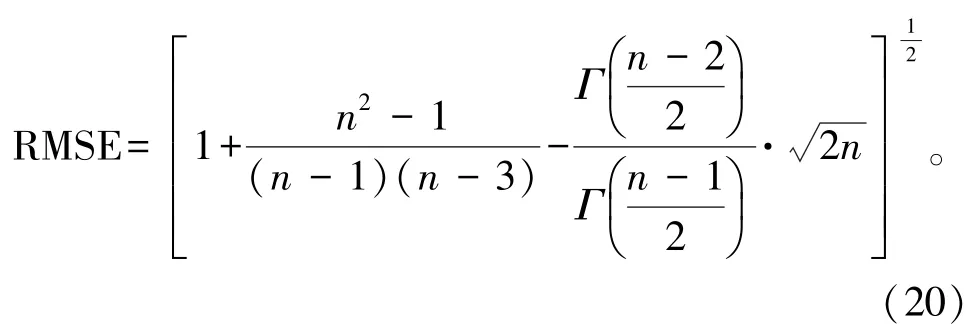
根据式（19）和式（20）可知，当大坝防洪特征水位序列Yf服从正态分布时，其统计指标MSE和RMSE与正态分布参数μ和σ2无关，而仅仅取决于样本容量n。其中RMSE随n（n≥4）呈单调递减，当n＝4时，RMSE达到最大。

2．3 复核指标的定义

通过有限样本容量n的实测洪水资料设计出的防洪特征水位，其设计标准常通过设计洪水频率或风险率来表示，而对于设计依据即设计资料（包括历史洪水、实测洪水和随机模拟洪水）的可靠度并未做定量分析。鉴于此，针对大坝防洪特征水位序列Yf的分布特性，本文基于洪水资料和防洪特征水位的双可靠度来复核大坝防洪特征水位。第1个可靠度为防洪特征水位序列的可靠度，本质是反映了洪水样本资料（容量为n且n≥4）的可靠度，其定义式为

同理，洪水样本资料的可靠度α与正态分布参数μ和σ2均无关，而仅仅取决于样本容量n。

第2个可靠度为第i个设计防洪特征水位（以第i年年最大洪水为设计典型洪水，共有n年）的可靠度，其定义式为

β＝Φ( zi)×100% 。（22）

式中：zi为经过式（5）标准化后的第i个设计防洪特征水位值；Φ（·）为标准正态分布函数。

3 三峡大坝防洪特征水位复核分析

三峡大坝以防洪、发电、航运为主要功能，其中发电、航运服从于防洪安全。三峡水库进入正常运行期以后的防洪调度方式，可分为对荆江进行防洪补偿调度、对城陵矶进行防洪补偿调度和优化调度3种，本次采用《三峡水库优化调度方案》［8］（水建管［2009］519号）的防洪优化调度方案研究三峡大坝防洪特征水位的设计。三峡水库防洪优化调度方案为：①当水库水位在145～155 m之间时，预留防洪库容56．5 亿m3，按控制莲花塘站水位不高于34．4 m对城陵矶进行防洪补偿调度；②当水库水位在155～171 m之间时，按沙市水位不要高于44．5 m对荆江进行补偿调度；③当水库水位在171～175 m之间时，为特大洪水预留防洪库容39．2亿m3，控制补偿枝城站流量不超过80 000 m3／s，控制沙市站水位不高于45．0 m；④按上述方式调度时，如相应的枢纽总泄流能力（含电站过流能力）小于确定的控制流量，则按照枢纽总泄流能力泄流。三峡大坝汛限水位为145．0 m，大坝按1 000 a一遇设计，10 000 a一遇加10%校核，其原设计防洪特征参数详见表1。

表1　三峡水库原设计防洪特征参数Table 1 Characteristic parameters of flood prevention designed for Three Gorges reservoir（TGR）　m

3．1 洪水样本资料分析

现有经过还原计算的宜昌站1882—2009年逐日洪水过程资料。按30d洪量最大的选样原则每年选择一场历时为30 d的最大洪水过程，构成样本容量为128 a的30 d洪水过程系列。与原设计洪水成果［9］相比，洪水系列延长至2009年后，日均流量和洪量减少1%～2%，设计洪峰和洪量减少0．7%～2．3%，因此为不降低原设计防洪标准仍采用原设计洪水成果，结果详见表2和表3。

表2　三峡水库原设计洪水统计参数（序列年限1877—1990年）Table 2 Statistic parameter values of design flood in TGR （1877—1990）

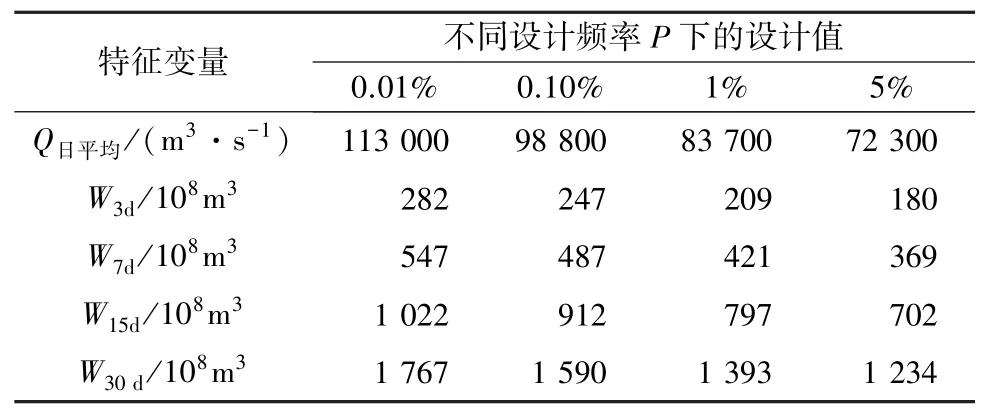
表3　三峡水库原设计洪水的不同设计频率下设计值（序列年限1877—1990年）Table 3 Design values for different frequencies of original design flood in TGR（1877—1990）

以设计频率0．01%（＋10%）按同倍比法（最大30 d洪量控制）推求的设计洪水过程作为三峡大坝校核洪水位的设计依据。取1882—2009年实测年最大洪水过程，组成年份连续的样本容量分别为30 a（样本个数＝128－30＋1＝98）、60 a（样本个数＝128－60＋1＝69）、90 a（样本个数＝128－90＋1＝39）和120 a（样本个数＝128－120＋1＝9）的4组典型洪水样本来分析样本容量n对防洪特征水位设计的影响。如样本容量为120 a的9个样本的组成年份分别为：1882—2001年、1883—2002年、1884—2003年、1885—2004年、1886—2005年、1887—2006年、1888—2007年、1889—2008年、1890—2009年。

3．2 复核分析

以校核洪水位可靠度分析为例，将4个样本容量（30，60，90，120 a）的校核洪水过程线作为调洪演算输入，按防洪调度规则进行调洪演算，统计各样本容量下的调洪高水位，即为校核洪水位。图1给出4个样本容量下校核洪水位的统计箱图，直观显示了校核洪水的均值、四分位数和极值等分布特征。图2给出4个样本容量下校核洪水位的正态分布概率密度曲线。据图1和图2可知，随着样本容量的增加，校核洪水位序列的均值增大，均方差也增大，即随机波动的浮动增大，且正态分布概率密度曲线越来越矮胖。

图1　校核洪水位的统计箱图Fig．1 Box plot at exceptional flood level

统计了4个样本容量下设计资料的可靠度和原校核洪水位可靠度，结果列于表4。据表4可知：

（1）随着样本容量的增加，洪水的信息量增大，设计资料的可靠度α提高。

图2　校核洪水位的正态分布概率密度曲线Fig．2 Probability density curves of normal distribution for exceptional flood level under different sample sizes

表4　4个样本容量下双可靠度结果Table 4 Results of dual reliability under four sample sizes

（2）当校核洪水位序列最大值不大于原校核洪水位180．4 m时，原校核洪水位的可靠度β也随着样本容量的增加而提高。

（3）α与β均随n单调递增，当n＝30时，α为85．46%，β为96．77%；n＝120时，α为93．19%，β为99．17%；当校核洪水位序列最大值不大于原校核洪水位180．4 m且n→＋∞时，有α→100%和β→100%。

（4）复核的设计成果（1877—2009年）与三峡水库初设阶段成果（1877—1990年）相比，尽管加入了1998年大洪水，但1999—2009年整体偏枯，水文序列延长后的最大日均流量及时段洪量均值减小3%以内，各频率设计洪水成果有所减小，减小幅度在4%以内，其中最大日均流量设计成果减小1%左右，3 d和7 d设计洪量减小在2%以内，15 d和30 d设计洪量减小3%左右，因此原防洪特征水位的可靠度β有所提高。

为可视化可靠度α与正态分布参数μ和σ2无关，而仅仅取决于样本容量n，采用随机模拟法验证式（20）和式（21）。首先随机生成服从标准正态分布Msimu＝50 000个样本容量为n（如30，60，90，120 a）的校核洪水位序列Z，另一个标准化后的校核洪水位序列为通过实测洪水资料调洪演算统计得到；然后计算RMSE以反映2个标准化后序列Z和的差异性；最后采用式（21）计算可靠度α。需要说明的是因前文已证明可靠度α与正态分布参数μ和σ2无关，所以此处用标准正态分布生成校核洪水位序列Z以免去非标准化序列进行标准化的步骤。图3给出了设计资料可靠度α随样本容量n变化的过程线（图3中的可靠度α分别为采用式（21）计算的理论值和采用洪水样本资料计算的实测值）。图3表明：可靠度α的理论值和实测值具有较好的拟合效果，验证了可靠度α与正态分布参数μ和σ2无关，而仅仅取决于样本容量n。

图3　设计资料可靠度随样本容量变化的过程线Fig．3 Variation of reliability of design flood data with sample size

4 结 语

本文采用水库调洪演算的随机微分方程推求防洪特征水位的概型，以三峡大坝为例，通过调洪演算将洪水不确定性转换为防洪特征水位的不确定性，以分析大坝防洪特征水位的分布规律，并基于双可靠度复核了三峡大坝防洪特征水位。主要结论如下：

（1）随着样本容量的增加，洪水的不确定性增大，三峡大坝设计资料的可靠度α和原校核洪水位的可靠度β均有所提高。

（2）可靠度α与正态分布参数μ和σ2无关，而仅仅取决于样本容量n。

参考文献：

［1］ 梅亚东，谈广鸣．大坝防洪安全的风险分析［J］．武汉大学学报（工学版），2002，35（6）：11－15．

［2］ 丁 晶，邓育仁，侯 玉，等．水库防洪安全设计时设计洪水过程线适用性的探讨［J］．水科学进展，1992，3（1）：45－52．

［3］ 姜树海．水库调洪演算的随机数学模型［J］．水科学进展，1993，4（4）：294－300．

［4］ 徐 敏，胡良剑，丁永生，等．随机微分方程数值解在泄洪风险分析中的应用［J］．数学的实践与认识，2006，36（9）：154－157．

［5］ 闫宝伟，郭生练．考虑洪水过程预报误差的水库防洪调度风险分析［J］．水利学报，2012，43（7）：803－807．

［6］ MOOD A M，GRAYBILL F A，BOES D C．Introduction to the Theory of Statistics［M］．Tokyo：McGraw⁃Hill，1974．

［7］ CANCELLIERE A，BONACCORSO B．Uncertainty Analy⁃sis of the Standardized Precipitation Index in the Presence of Trend［J］．Hydrology Days，2009，（1）：14－26．

［8］ 中华人民共和国水利部．三峡水库优化调度方案［R］．北京：中华人民共和国水利部，2009．

［9］ 长江水利委员会．三峡工程水文研究［M］．武汉：湖北科学技术出版社，1997．

（编辑：姜小兰）

Recheck of Characteristic Flood Level for Built Reservoir after Extension of Hydrologic Time Series

ZHOU Yan⁃lai1，2，3，CHEN Jin1，2，XU Ji⁃jun1，2
（1．Water Resources Department，Yangtze River Scientific Research Institute，Wuhan 430010，China；2．Key Lab of Basin Water Resource and Eco⁃environmental Science in Hubei Province，Yangtze River Scientific Research Institute，Wuhan 430010，China；3．State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China）

Abstract：In order to explore the influence of uncertainty of flood on design of characteristic flood level for dam，we derive probability distribution of characteristic flood level（CFL）for dam by using stochastic differential equation for calculation of flood regulation．Three Gorges reservoir is selected as a case study．The uncertainty of flood is transformed into that of CFL so as to analyze probability distribution of CFL through calculation of flood regulation．On this basis，we recheck the CFL of Three Gorges reservoir．The results show that，1）reliabilities of design flood data and original exceptional flood level（180．4 m）increase with the increase of sample size；2）under sample size of 120a，reliability of design flood data and reliability of CFL are 93．19%and 99．17%，respectively．Finally，the research results provide theoretical basis for improvement in safety design of dam reservoir．

Key words：hydrologic time series；characteristic flood level；uncertainty；stochastic differential equation；recheck of characteristic flood level；Three Gorges Reservoir

作者简介：周研来（1985－），男，湖南娄底人，工程师，博士，主要从事水文学及水资源开发利用研究，（电话）027－82927557（电子信箱）zyl23bulls＠whu．edu．cn。

基金项目：国家自然科学基金项目（51509008）；湖北省自然科学基金项目（2015CFA157，2015CFB217）；“湖北省高端人才引领培养计划第一层次人选”计划项目（2013—2017）；武汉大学水资源与水电工程科学国家重点实验室开放基金资助项目（2014SWG02）

收稿日期：2014－10－28；修回日期：2015－02－06

中图分类号：TV697．1；TV73

文献标志码：A

文章编号：1001－5485（2016）03－0014－05