华北汛期降水分离时间尺度降尺度预测模型的改进

阮成卿李建平

1中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京1000292中国科学院大学，北京1000493北京师范大学全球变化与地球系统科学研究院，北京1008754全球变化研究协同创新中心，北京100875



华北汛期降水分离时间尺度降尺度预测模型的改进

阮成卿1, 2李建平3, 4

1中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室，北京100029
2中国科学院大学，北京100049
3北京师范大学全球变化与地球系统科学研究院，北京100875
4全球变化研究协同创新中心，北京100875

摘 要本文采用偏相关预报因子挑选法和条件降尺度法，对已有的华北汛期（7～8月）降水时间尺度分离（TSD）降尺度模型进行了改进。利用偏相关法，找到一个新的影响华北汛期降水年际分量的前期预报因子，即6月北大西洋—欧亚遥相关（AEAT）。该因子将扰动信号储存于北大西洋三极子结构，并在7～8月释放出来影响下游贝加尔湖低压系统的发展，从而影响华北汛期降水。利用6月Niño3指数和AEAT指数，本文建立了条件TSD统计降尺度模型，即按照预报因子的强度进行逐年分类，对于每个分类设计相应的预报模型，从而避免信息较弱因子的干扰。条件TSD降尺度方法显著改善了华北汛期降水的预测技巧，在独立检验阶段，预报降水与观测降水的相关系数由原模型的0.61提高到0.77，符号一致率从70%提高到87%。

关键词华北汛期降水 分离时间尺度 偏相关 条件降尺度

资助项目 中国科学院战略性先导科技专项子课题XDA05090403，国家自然科学基金资助项目41375110、41475076

Funded by “Strategic Priority Research Program—Climate Change: Carbon Budget and Relevant Issues”of the Chinese Academy of Sciences (Grant XDA05090403), National Natural Science Foundation of China (Grants 41375110 and 41475076)

An Improvement in a Time-Scale Decomposition Statistical Downscaling Prediction Model for Summer Rainfall over North China

RUAN Chengqing1, 2and LI Jianping3, 4

1 State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029
2 University of Chinese Academy of Sciences, Beijing 100049
3 College of Global Change and Earth System Science, Beijing Normal University, Beijing 100875
4 Joint Center for Global Change Studies, Beijing 100875

Abstract This paper applies partial-correlation predictor selection and a conditional downscaling method to improve a Time-Scale Decomposition (TSD) statistical downscaling model of summer (July and August, JA) rainfall over North China. A new preceding predictor, the North Atlantic–Eurasia Teleconnection (AEAT) in June is found by using the partial-correlation predictor selection method. This predictor stores its signal in the tripole sea surface temperature pattern in the North Atlantic and impacts on the development of depressions over Baikal in the following July and August, which further influences the rainfall over North China. A conditional TSD statistical downscaling model is built with thepredictors of Niño3 index and AEAT Index (AEATI). Rather than fixed models for every year, indices are classified into several types according to the predictor strength, and corresponding models are built for each type. The conditional statistical model avoids the influence from weak predictors for a particular year. In independent validation, the conditional TSD downscaling model improves the performance of Summer Rainfall over North China (NCSR) prediction. The correlation coefficient between observed and predicted rainfall increases from 0.61 to 0.77 and the anomaly sign consistency rate increases from 70% to 87%.

Keywords North China summer rainfall, Time-scale decomposition, Partial correlation, Conditional downscaling

1 引言

华北地区是我国的农业主产区，人口密集，经济发达，地处副热带，东临太平洋，夏季降水集中在7月和8月，并受东亚夏季风影响（Li and Zeng, 2002L; Li and Zeng, 2003；黄荣辉等，2006）。自上世纪70年代以来，华北降水显著减少，给当地的生产、生活和生态环境带来影响（Xia et al., 2007）。而近十年来，华北汛期降水又有回升的趋势（Guo et al., 2012; 李建平等，2013）。华北降水变化的复杂性和影响的重要性表明，建立有效的降水预报模型有重要的应用价值。

统计降尺度是研究区域气候问题的常用方法（Yarnal et al., 2001, Fowler et al., 2007, Nicholas and Battisti, 2012），该方法通过建立大尺度环流预报因子与局地预报量的统计关系（Giorgi and Mearns, 1991, Hewitson and Crane, 2006），来对局地气候进行预测（Li and Smith, 2009; Guo et al., 2011; Liu et al., 2011; Sauter and Venema, 2011; García-Bustamante et al., 2012; Guo et al., 2012）。而大尺度环流信息通常来自大气环流模式（General circulation models, GCMs）的模拟，这将不可避免的引入模式误差。但如果统计降尺度方法从前期信号中寻找预报因子，建立该因子与区域气候的统计关系，则可不依赖于GCMs的模拟能力，有利于对局地降水做出更准确的预测。

一个物理现象有多种时间尺度变率特征，而不同变率往往不是同一外强迫因子调控的结果。因此有必要对物理现象按时间尺度分解，分别研究各尺度的影响机制和预报模型，再将不同模型的结果叠加作为对物理现象的预测，这就是时间尺度分离（Time-scale decomposition, TSD）的降尺度预测方法（李建平等，2013）。研究表明，华北汛期降水同时有显著的年际变率和年代际变率（陆日宇，2002），因此，前人建立了TSD统计降尺度预测模型（Guo et al., 2012）。结果显示，年际尺度上华北汛期降水与前期6月赤道中东太平洋（5°S～5°N, 150°W～90°W）的海温密切相关，其可在西北太平洋的低层大气激发异常环流从而影响华北降水；年代际尺度上在东印度洋—西太平洋暖池海温的作用下，华北降水与前期6月西南印度洋海平面气压有同步变化关系。分别建立华北汛期降水年际和年代际的预测模型，并将两者之和作为总降水预测值。TSD统计降尺度模型显示出较好的预测效果，并正确预测了随后几年（2011～2013年）的华北降水（李建平等，2013）。

华北汛期降水TSD模型中已经发现6月Niño3指数是预测年际变量降水的有效预报因子，但局地气候可能受多个外强迫因子的影响，那么是否还有其他预报因子能用于降水预测？在寻找新的预报因子时，为了避免Niño3指数的干扰，本文提出偏相关的预报因子选取法，将Niño3指数的信号从降水序列中线性剔除，用降水的剩余部分来寻找下一个预报因子。通过这种方法寻找的预报因子，是与Niño3指数未能解释的降水变率部分紧密联系的，从而对Niño3指数因子进行补充，这可以不断提高统计模型的技巧。另外，因为新因子和Niño3指数分别与降水序列中不同部分的变率相对应，所以通过这种方法找到的因子，也能间接的保证其与Niño3指数的独立性。

当局地降水受多个预报因子调控时，预报因子之间可能产生干扰，直接建立降水与预报因子之间的多元线性回归模型并不合理。因为不同预报因子提供的信息强弱是逐年变化的，当预报因子信息较强时，该预报因子引起的气候强迫范围也更大，效果更强，波及更远；而当预报因子较弱时，其影响效果就较小，应该被忽略。尤其是对遥相关类的预报因子，这种现象更明显。为此，本文提出条件TSD降尺度的概念：在不同条件下，统计降尺度模型所使用的预报因子和预报方程并不固定，而是根据每年各个预报因子提供信息的强弱来判断，做出具体的选择。这样某年信息较弱的预报因子在该年预测时会被忽略，避免其对该年降水预测产生干扰。

本文主要工作是对已有的华北降水TSD降尺度模型的年际部分进行改进。利用偏相关方法来寻找新的影响降水年际变率的前期预报因子，建立条件TSD统计降尺度模型来进行预测，并与原模型进行比较。

2 数据

本文采用的降水数据为中国气象局气候中心整理的中国160测站7～8月月平均降水资料（1951～2013年）。华北区域的选择为（35°N～40°N，110°E～122°E），其内共有15个测站（安阳、北京、长治、德州、菏泽、济南、临汾、临沂、青岛、石家庄、太原、天津、潍坊、邢台、烟台），将15个测站7～8月平均降水量定义为华北汛期降水（Summer Rainfall over North China; NCSR）序列。

本文所采用的气象环流场资料为NCEP/NCAR（美国国家环境预测中心/国家大气研究中心）再分析资料，水平分辨率为2.5°×2.5°，垂直分层为17层（Kalnay et al., 1996）；海表面温度（Sea surface temperature, SST）资料为Hadley中心提供的第一套月平均海表面温度资料，水平分辨率为1°×1° （Rayner et al., 2003）；使用的Niño3指数来自美国国家海洋和大气管理局（http://www.cpc.noaa.gov/ data/indices [2015-01-05]）。所有数据均为月平均数据。

3 方法

华北汛期降水同时有明显的年际和年代际变率，因此应当建立TSD统计降尺度模型。本文将降水及其他数据按照傅里叶分解的方式，得到不同时间尺度的分量，将周期小于或等于7年的高频部分作为年际分量，周期大于7年的低频部分作为年代际分量。对这两种尺度的降水分量分别建立年际、年代际变率的降尺度模型，具体原理及步骤参见Guo et al.（2012）和李建平等（2013）。本文主要针对年际模型进行改进，年代际尺度上仍使用原模型。

已有的TSD降尺度模型显示，Niño3指数是预测NCSR年际变率的有效预报因子，所以本文采用偏相关法寻找新的预报因子。首先建立Niño3指数与NCSR的线性回归模型：

其中，A表示各变量的年际分量，波浪上划线~表示回归模型的估计值。然后将Niño3指数解释的降水变率从原降水序列中去除：

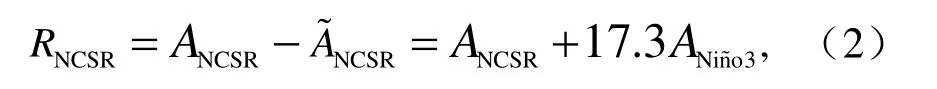
得到与Niño3指数无关的剩余NCSR降水量RNCSR。用RNCSR与环流场进行相关分析，来寻找新的预报因子。

当多个预报因子被选入统计模型后，对预报因子指数做标准化处理，用指数的绝对值作为衡量每年因子信息强弱的指标。然后按照指数对预报因子进行分类，对于每一类个例分别建立相应的统计关系，得到条件TSD统计降尺度模型。进行实际预测时，按照每年预报因子指数大小，选择对应的预报模型，以提高预报技巧。

观测资料共有63年（1951～2013年），选取前40年（1951～1990年）作为预报因子的挑选和模型的拟合阶段，用剩余的23年（1991～2013年）作为模型的独立检验阶段。

4 北大西洋—欧亚遥相关（AEAT）因子的选入及其对NCSR的影响机制

4.1 AEAT因子的选入

将扣除Niño3指数信号的7～8月RNCSR与6月环流场做相关分析，来寻找影响该部分降水变率的前期预报因子（图1）。分析结果显示，在气压场上，北大西洋东部呈现NAO（北大西洋涛动）负位相结构，中纬度部分为负相关，高纬度部分为正相关（Li and Wang, 2003）。北大西洋北部，有一沿欧亚大陆北侧向下游传播的波列结构，该结构在对流层中层（图1b）尤其明显，可影响至东亚中部地区。这种波列结构与AEAT（North Atlantic–Eurasia Teleconnection）的结构相类似（李建平等, 2013），前人研究指出AEAT是夏季北大西洋影响东亚夏季风的途径之一（Wu et al., 2009; Wu et al., 2012）。在SST场上，由于Niño3指数因子的去除，热带东太平洋没有明显的高相关区；但在北大西洋东部区域，中部为SST显著负相关区，北部为SST显著正相关区（图略）。

将图1中各个高相关区（虚线方框所示）的物理量面积加权平均定义为潜在预报因子指数。对于图1b中欧亚大陆北侧波列相关区，因其与AEAT结构相似，将这四个区域平均的位势高度（H）根据相关系数的符号定义为AEAT指数：

下标A、B、C、D分别代表北大西洋北部、欧洲东北部、中亚地区和东亚东部地区四个活动中心（图1b）。对IAEAT和其他潜在预报因子分别与RNCSR进行剔除一个的交叉检验（Guo et al., 2011; Guo et al., 2012），并计算均方根误差（Root-mean-square error，RMSE）。其中IAEAT因子具有最小的RMSE，为40.3 mm，并且其与NCSR的相关系数为0.57，达到99%信度水平（表1）。IAEAT是去除ENSO信号后与NCSR相联系的预报因子，将其选入华北汛期降水年际模型。

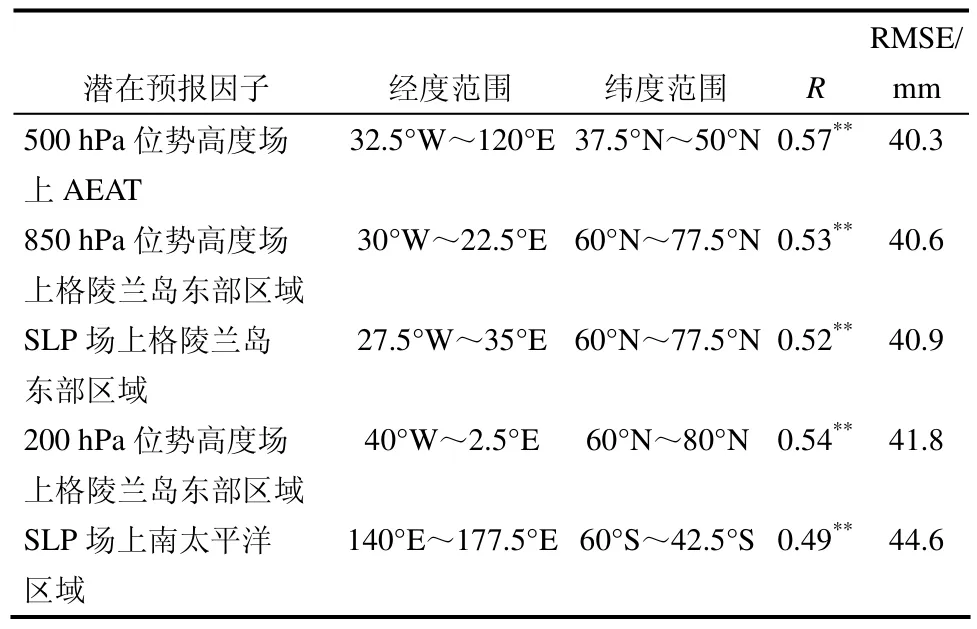
表1 因子选择阶段（1951～1990年）均方根误差最小的5个潜在年际预报因子及其所在区域。R为预报因子与NCSR的相关系数；RMSE为剔除一个交叉检验过程中观测与拟合的NCSR之间的均方根误差，单位：mmTable 1 Five potential interannual predictors with the minimum RMSE in predictor selection of period 1951–1990 and their locations. R is the correlation coefficient between potential predictors and NCSR (Summer Rainfall over North China); RMSE is the root-mean-square error between observed and fitted NCSR in the leave-one-out cross validation, unit: mm

4.2 6月AEAT对7～8月NCSR的影响机制

AEAT与华北汛期降水的年际部分有较好的相关性，那么6月的预报因子是如何影响7～8月降水的呢？大气系统的记忆性较弱，而海洋的异常信号往往能持续一个季节（Nan et al., 2009；郑菲和李建平，2013）。Wu et al.（2009）和Wu et al.（2012）等发现，春季时NAO可在北大西洋强迫产生海温三极子结构，夏季时三极子海温可影响下游的东亚夏季风的强度，进而影响长江汛期降水。那么6月 AEAT是否也有类似的海洋强迫作用？

图2为6月IAEAT与同期500 hPa位势高度场和SST场的年际相关分析。由此可见，在北大西洋上空，位势高度场呈现NAO负位相结构；在欧亚大陆北侧，波列状结构经欧洲东北部、中亚地区传播至东亚地区，中国大部分地区为位势高度负相关。在同期的SST场上，北大西洋地区中部为负相关，两侧为正相关。可见，6月AEAT也可以在海温场上强迫产生三极子结构，与春季NAO的海温强迫相似（Wu et al., 2009; Wu et al., 2012）。这种海温异常可能是将6月信号持续至7～8月的关键，故定义北大西洋海温三极子指数（Tripole SST index，ITSST）：

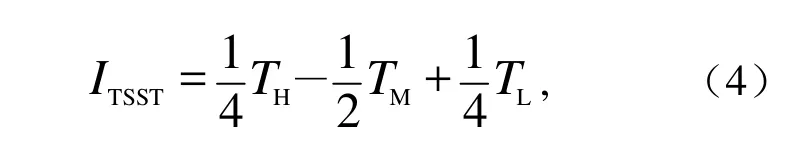
等号右侧分别代表北大西洋高纬度、中纬度和低纬度三个中心的海表温度。6月IAEAT与ITSST的相关系数为0.35，达到99%的信度水平（表2）。

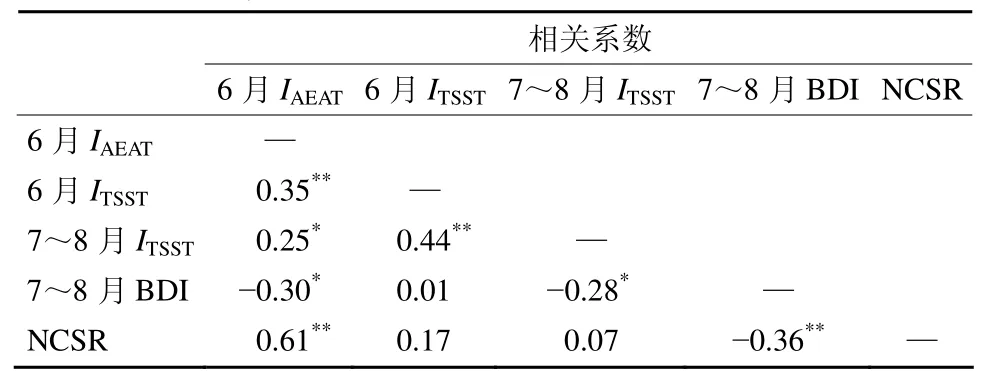
表2 1951～2013年，年际部分的6月IAEAT、6月ITSST、7～8月ITSST、7～8月贝加尔湖低压指数BDI （37.5°N～47.5°N，85°E～105°E）区域平均的500 hPa位势高度）和NCSR的年际交叉相关Table 2 Cross correlation between interannual components of IAEAT(AEAT index) in June, ITSST(Tripole SST index) in June, ITSSTin JA, and BDI (Baikal depression index, area-weighted mean of 500-hPa geopotential height over 37.5°N−47.5°N, 85°E−105°E ) in JA and NCSR

图3a、b分别为6月和7～8月ITSST与同期SST场的年际相关分析，可见不论6月还是7～8月，北大西洋海温的三极子结构都是存在的，而且两者的相关系数为0.44，达到99%的信度水平（表2）。那么7～8月的三极子结构是否就是由6月的海温异常持续而来？为此，我们首先从6月海温变率中分解出能够持续到7～8月的部分：

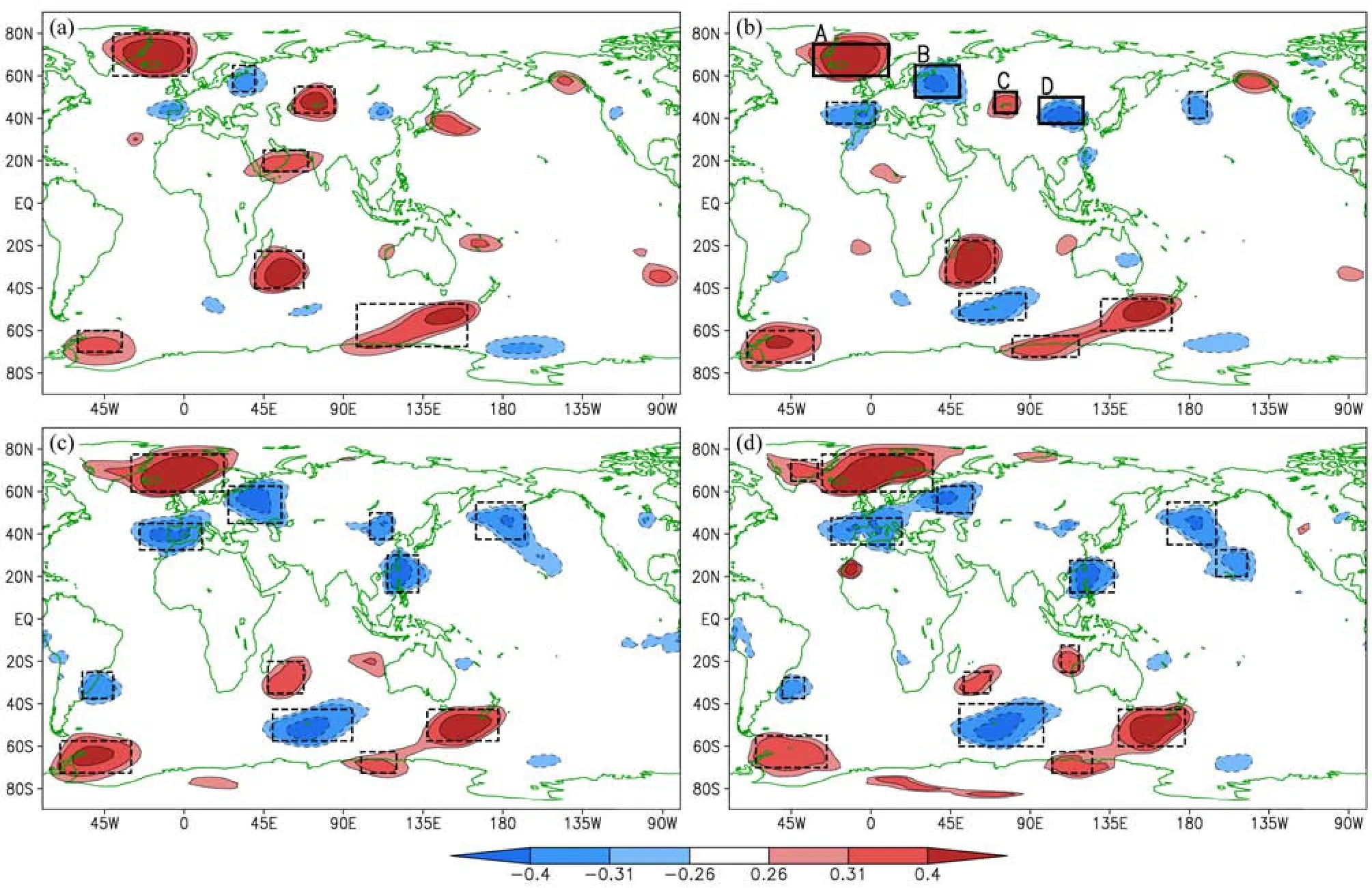
图 1 7～8月NCSR与6月环流场年际部分变量相关图（去除了ENSO信号）：（a）200 hPa位势高度场；（b）500 hPa位势高度场，欧亚大陆上实线方框代表AEAT的中心；（c）850 hPa位势高度场；（d）SLP（sea level pressure）场。等值线表示相关系数；(±)0.26～(±)0.31区域、(±)0.31～(±)0.40区域、＞0.40（＜−0.40）区域分别达到90%、95%和99%信度水平；每个虚线方框为潜在预报因子Fig. 1 Correlation maps between interannual components of NCSR in JA (July and August) and relevant circulation fields in June after removing the signal of ENSO during 1951–1990: (a) 200-hPa geopotential height; (b) 500-hPa geopotential height, the solid boxes over Eurasia are the centers of AEAT (the North Atlantic–Eurasia Teleconnection); (c) 850-hPa geopotential height; (d) SLP (sea level pressure). The contours represent correlation coefficients; (±)0.26–(±)0.31 area, (±)0.31–(±)0.40 area, and＞0.40（＜−0.40）area indicate statistically correlation above the 90%, 95% and 99% confidence levels, respectively; the dashed boxes are the regions of potential predictors

图2 6月IAEAT与6月（a）500 hPa位势高度场（方框代表AEAT区域）和（b）SST场（方框代表海温三极子区域）的年际相关图。打点区域达到95%信度水平Fig. 2 Correlation maps between interannual components of June IAEATand (a) 500-hPa geopotential height (boxes indicate the areas of AEAT) and (b) SST (boxes indicate the areas of Tripole SST) in June. Stippled areas indicate statistically significant correlation above the 95% confidence level

其中，T表示海表面温度；t表示6月，t+1表示7～ 8月；Cov和Var分别表示协方差与方差（Pan, 2005; Wu et al., 2009）。然后将6月持续海温（Tp）和6月总海温（T(t)）分别与7～8月ITSST做回归分析，并比较两者海温三级子结构的形态。结果如图3c、d所示，北大西洋三极子海温的分布型在两个图中并未有明显变化，在Tp中仅强度略有减弱。可见6月北大西洋三极子可以持续至7～8月，从而可以将6月AEAT的强迫信号传递至随后的7～8月。

图3 （a）6月ITSST与6月SST场年际相关图。（b）同（a），但为7～8月ITSST与7～8月SST场。（c）回归到7～8月ITSST的6月SST异常的持续部分，单位：°C。（d）同（c），但为6月全部SST。图中打点区域达到95%信度水平，方框代表北大西洋海温三极子区域Fig. 3 (a) Correlation map between interannual components of ITSSTin June and SST in June (b) Same as (a), but for ITSSTand SST in JA. (c) Interannual component of persistence SST anomaly (units: °C) regressed on ITSSTin JA. (d) Same as (c), but for total SST in June. Stippled areas indicate statistically significant correlation above 95% confidence level, boxes indicate the areas of TSST

7～8月北大西洋三极子海温异常会对下游气候产生什么影响？图4a为7～8月ITSST与7～8月500 hPa位势高度场的年际相关分析。可见在7～8月时三极子海温能在中纬度地区强迫产生波列结构，活动中心分别位于北大西洋中部、欧洲西北部、黑海地区、中亚地区和贝加尔湖南侧地区，而贝加尔湖南侧的低压系统与中国北方降水密切相关（赵声蓉和宋正山，1999）。将37.5°N～47.5°N，85°E～105°E区域平均的500 hPa位势高度定义为贝加尔湖低压指数（Baikal depression index，BDI），该指数与7～8月ITSST的相关系数为−0.28，达到95%信度水平（表2）。BDI与整层水汽输送通量的相关分析显示（图4b），当BDI偏强时，存在以贝加尔湖为中心的气旋式结构，而华北地区位于气旋结构的东南侧，盛行西南风，从而将中国西南的水汽输送至华北地区，有利于华北降水的产生（图4c）。而且BDI与NCSR的相关系数为−0.36，也达到99%信度水平（表2）。

以上分析给出了6月北大西洋—欧亚遥相关影响7～8月华北降水的物理机制，即6月AEAT首先将异常信号储存至北大西洋海温三极子结构中，然后在7～8月释放出来，调控贝加尔湖低压系统的发展，再通过影响水汽输送来影响华北汛期降水。

4.3 含有AEAT因子的TSD模型

6月AEAT可通过北大西洋三极子海温结构来影响7～8月华北降水，下面将6月IAEAT引入TSD统计降尺度模型的年际部分，利用1951～1990年观测数据，建立年际分量的二元线性回归模型：

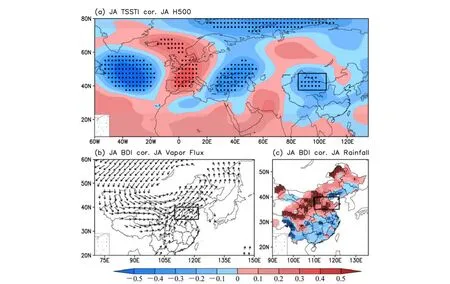
图4 （a）7～8月ITSST与7～8月500 hPa位势高度场的年际相关，打点区域达到95%信度水平，方框代表贝加尔湖低压区域。（b）7～8月BDI与7～8月整层水汽输送通量的年际相关，箭头表示达到95%信度水平，方框代表华北区域。（c）7～8月BDI与7～8月降水的年际相关，打点区域达到95%信度水平，方框代表华北区域Fig. 4 (a) Correlation map between interannual components of ITSSTin JA and 500-hPa geopotential height in JA, stippled areas indicate statistically significant correlation above 95% confidence level, the box indicates the area of Baikal depression. (b) Correlation map between interannual components of BDI in JA and all-level water vapor transport flux in JA, arrows indicate statistically correlation above 95% confidence level, the box indicates the area of North China. (c) Correlation map between interannual components of BDI in JA and rainfall in JA, stippled areas indicate statistically correlation above 95% confidence level, the box indicates the area of North China

其中，A表示各变量的年际分量，波浪上划线~表示回归模型的估计值。将模型在1991～2013年进行独立检验，结果显示（图5a、表3），相对于仅使用Niño3指数一个预报因子，引入IAEAT的新模型的预报效果有较大提升。对于年际部分降水，相关系数由0.56提升至0.73，RMSE由46.8 mm降低至39.7 mm，符号一致率也从74%提升至83%。叠加上年代际模型的预测结果后，含有AEAT指数的模型对总降水的预测效果也优于原模型。

5 条件TSD模型的建立及其与原模型的比较

5.1 按照强度对预报因子分类

对华北降水的年际部分，本文找到了新的预报因子IAEAT指数，但直接建立二元回归模型是否是最优的？Niño3指数与AEAT都是通过遥相关作用影响华北汛期降水，如果某年预报因子强度偏低，则其影响也较弱。在这种情况下，若模型中仍考虑该因子作用，则会引入无用信息，降低模型预报技巧。

图6为NCSR与Niño3指数和IAEAT年际分量的散点图，由图可见，两个预报因子与NCSR都有显著的相关。但是仅当Niño3指数强度超过0.5时（图6a），散点才集中在第二、四象限；而对于（−0.5，0.5）区间的散点，则较为随机的分布在各个象限。同样的现象在图6b中也有发生，当IAEAT介于（−0.5，0.5）之间时，其与NCSR的相关性并不显著。因此对于华北汛期降水而言，应当按照条件降尺度的方法，分情况来建立统计模型。

以0.5为阈值，将1951～2013年共63个个例分成Niño3指数强弱年和IAEAT强、弱年，并进行组合。考虑到当两个因子同时较强时，其强迫效果可能叠加或相消，故对这种情况又按照符号相同或相反分成两类（图7），结果如下（图8）：

表3 在拟合阶段（1951～1990年）与检验阶段（1991～2013年），新旧TSD模型对NCSR的模拟能力的比较。TSD模型包括仅使用Niño3指数模型、Niño3指数与IAEAT指数模型和条件TSD模型。R为观测与预测NCSR之间的相关系数；RMSE为观测与拟合降水的均方根误差，单位：mm；P为降水距平符号一致率Table 3 Comparison of performances of old and new TSD models for NCSR simulation during the training period (1951–1990) and the independent validation period (1991–2013). TSD models include the model with only Niño3 index the model with Niño3 index and IAEAT, and the conditional TSD model. R is the correlation coefficient between observations and NCSR. RMSE is the root-mean-square error between observed and fitted NCSR, unit: mm. P is the anomaly sign consistency rate

第一类为Niño3指数强而IAEAT弱年（图8a、b），共有17个个例。图8a中仅一个个例没有位于第二、四象限，且Niño3指数与NCSR的相关系数为−0.81，达到95%新度水平；而对于IAEAT，其与NCSR的相关系数仅为0.25，图8b的散点分布也无明显特征。可见对于Niño3指数强而IAEAT弱年，仅利用Niño3指数一个预报因子就足以对华北降水进行预报，而IAEAT因子并不能提供有效的信息。如果此时仍引入IAEAT因子，则只会增加随机误差。

第二类为Niño3指数弱而IAEAT强年（图8c、d），共有16个个例。此时Niño3指数与NCSR的相关系数仅为0.10，而IAEAT与NCSR的相关系数为0.72，仅有5个个例位于第二、四象限，由此可见，在这种条件下，仅使用IAEAT一个预报因子就可以解释NCSR的大部分变率，并不需要Niño3指数因子的引入。

第三类为Niño3指数与IAEAT都较弱的年（图8e、f）。此时NCSR与Niño3指数和IAEAT的相关系数分别为−0.40和0.52，都未能达到95%的信度水平。这表明当两个因子的强度均较弱时，这两个因子都不能对NCSR产生有效的强迫作用。但这一分类中仍有部分个例有较大的降水异常，可见对于这一类年，NCSR可能受其他因子的调控。

第四类为Niño3指数与IAEAT均强且异号的年（图8g、h），仅6个个例，而NCSR与Niño3指数和IAEAT的相关系数分别为−0.88和0.83，都达到95%的信度水平。此时Niño3指数和IAEAT都可为NCSR的预测提供信息，且强迫效果相同、相互叠加，从而使得两者与NCSR的相关系数都达到了较高的数值。但这类情况的个例较少，将不利于建立稳定的统计模型。

第五类为Niño3指数与IAEAT均强且同号的年（图8i、j）。此时共有11个个例，NCSR与两个预报因子的相关系数分别为0.38和0.55，均未能达到95%的信度水平。可能的原因是对于这些年，Niño3指数与IAEAT都有较大的强迫效果，但由于两个因子的作用相反、相互抵消，使得实际NCSR的预测更加复杂。

5.2 条件TSD模型的建立、检验与比较

根据以上分析，本文按照预报因子的强度提出不同的预报方案（图6）：方案一，对于强Niño3指数而弱IAEAT的年，仅使用Niño3指数作为预报因子；方案二，对于Niño3指数弱IAEAT强的年，仅使用IAEAT作为预报因子；方案三，其他三种类型情况较为复杂，各有其不利建模的问题，固将这些类型归为一类，使用Niño3指数和IAEAT两个预报因子。根据1951～1990年的观测数据，建立条件TSD降尺度统计模型的年际部分：

图 5 （a）NCSR年际部分时间序列（黑色为观测，红色为使用Niño3指数模型，绿色为Niño3指数与IAEAT指数模型，蓝色为条件TSD模型），模型拟合阶段为1951～1990年，独立检验阶段为1991～2013年，单位：mm。（b）同（a），但为年代际部分时间序列。（c）同（a），但为总降水时间序列Fig. 5 (a) Time series of the interannual components of NCSR from observations (black), the model with only Niño3 index (red), the model with Niño3 index and AEATI (green), and the conditional TSD model (blue), the training period is 1951–1990 and the independent validation period is 1991–2013. Units: mm. (b) As (a), but for the interdecadal components. (c) As (a), but for the total precipitation

图6 NCSR（单位：mm）与标准化的（a）Niño3指数和（b）IAEAT年际部分的散点图。N为个例次数，R为相关系数，星号表示达到95%信度水平Fig. 6 Scatter plots of interannual components of NCSR (units: mm) and standardized (a) Niño3指数 and (b) IAEAT. N is the case number and R is the correlation coefficient (* indicates statistically correlation at the 95% confidence level)

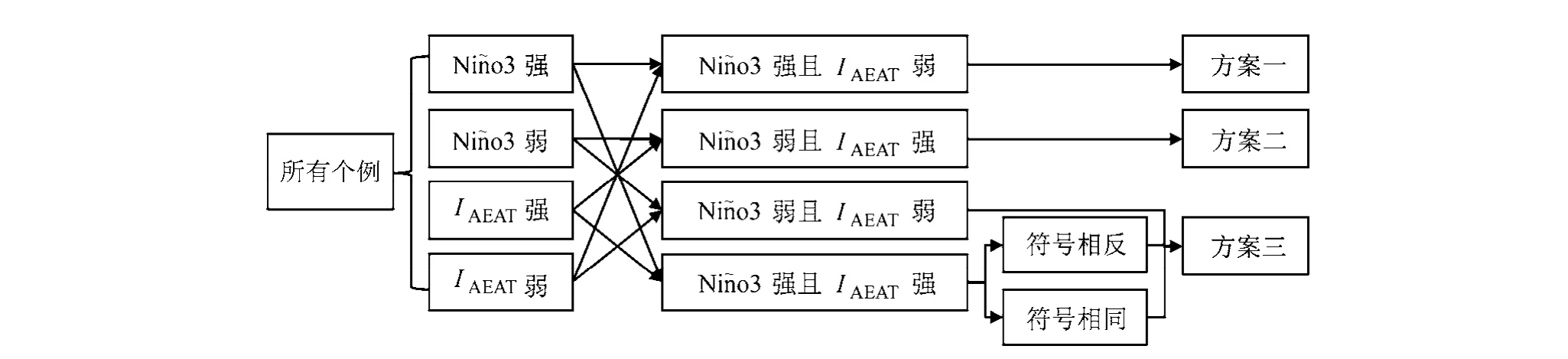
图 7 条件降尺度模型示意图Fig. 7 Schematic diagram of the conditional statistical downscaling model

图 8 同图6，但为（a）、（b）Niño3指数强而AEATI弱年，（c）、（d）Niño3指数弱而AEATI强年，（e）、（f）Niño3指数弱AEATI也弱年，（g）、（h）Niño3指数强AEATI也强且反号年，（i）、（j）Niño3指数强AEATI也强且同号年Fig. 8 As Fig. 6, but for (a, b) years of strong Niño3 index and weak AEATI, (c, d) years of weak Niño3 index and strong AEATI, (e, f) years of weak Niño3 index and weak AEATI, (g, h) years of strong Niño3 index and strong AEATI with opposite phases, and (i, j) years of strong Niño3 index and AEATI with the same phase

ANiño3和AAEATI均为标准化的预报因子年际分量。具体进行预报时，根据当年6月观测的ANiño3和AAEATI的强度，来选择相应预报方程。

利用1991～2013年的观测数据对模型进行独立检验，结果显示（图5和表3），相对于二元回归模型，条件TSD统计降尺度模型使华北汛期降水的预测技巧得到进一步的提升，年际分量的相关系数和符号一致率分别从0.73和83%提高到0.81和87%。对于总降水的预测，条件模型将相关系数从0.66提高为0.77，RMSE从56.9 mm降低到54.6 mm，符号一致率从78%提高到87%。可见，利用条件TSD降尺度模型，根据逐年的预报因子特点来选择合适的预报方程，优于直接的多元线性回归模型。

6 总结与讨论

本文对TSD模型的年际部分进行了改进，找到了一个新的影响华北汛期降水的前期预报因子，6 月AEAT。该因子可以在北大西洋强迫产生海温三极子结构，由于海洋的记忆性较强，三极子可将大气信号持续至7～8月，并对下游欧亚大陆产生强迫作用，调控贝加尔湖低压系统的发展，从而进一步影响华北降水。在此过程中，北大西洋海温三极子结构充当了海洋桥的作用（李建平等，2013）。而AEAT的强迫作用表明，在北半球夏季，北大西洋的异常信号也可传递到下游地区，影响局地气候的发展。因此在做夏季东亚短期气候预测时应考虑AEAT的作用。

利用Niño3指数和IAEAT两个指数，本文进一步提出了条件降尺度模型的概念。按照预报因子的强度，将多年观测分成若干类，对于每种类型针对性的建立各自的统计模型。进行实际预测时，按照当年预报因子的强度选择相应的预报模型，这样就能根据实际情况选择最优的方案，并能避免信息较弱预报因子的干扰。在模型的独立检验过程中，条件降尺度模型的预报效果也优于直接的线性回归模型。

也应注意到，虽然条件TSD降尺度模型在大多数年份做出了较好的华北汛期降水预测，但在某些极端年份，如1995年、1996年、1997年、1999年和2002年，统计模型的预测在降水距平大小上仍有偏差。这表明极端事件与一般事件有不同的特征，而本模型的不同预报方程都是基于线性回归模型，这可能是造成这些年份降水预报较差的原因。另外对于ENSO和AEAT指数都偏弱的年份，条件TSD模型未能提出很好的预报方案。对于这些年份是否还有其他预报因子影响华北降水，将是下一步的工作。

参考文献（References）

Fowler H J, Blenkinsop S, Tebaldi C. 2007. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling [J]. Int. J. Climatol., 27 (12): 1547–1578.

García-Bustamante E, González-Rouco J, Navarro J, et al. 2012. North Atlantic atmospheric circulation and surface wind in the northeast of the Iberian Peninsula: Uncertainty and long term downscaled variability [J]. Climate Dyn., 38 (1–2): 141–160. Giorgi F, Mearns L O. 1991. Approaches to the simulation of regional climate change: A review [J]. Rev. Geophys., 29(2): 191–216.

Guo Y, Li J P, Li Y. 2011. Statistically downscaled summer rainfall over the middle–lower reaches of the Yangtze River [J]. Atmos. Oceanic Sci. Lett., 4 (4): 191–198.

Guo Y, Li J P, Li Y. 2012. A time-scale decomposition approach to statistically downscale summer rainfall over North China [J]. J. Climate, 25 (2): 572–591.

黄荣辉, 陈际龙, 黄刚, 等. 2006. 中国东部夏季降水的准两年周期振荡及其成因 [J]. 大气科学, 30 (4): 545–560. Huang Ronghui, Chen Jilong, Huang Gang, et al. 2006. The quasi-biennial oscillation of summer monsoon rainfall in China and its cause [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 30 (4): 545–560.

Hewitson B C, Crane R G. 2006. Consensus between GCM climate change projections with empirical downscaling: Precipitation downscaling over South Africa [J]. Int. J. Climatol., 26 (10): 1315–1337.

Kalnay E, Kanamitsu M, Kistler R, et al. 1996. The NCEP/NCAR 40-year reanalysis project [J]. Bull. Amer. Meteor. Soc., 77 (3): 437–471.

Li J P, Zeng Q C. 2002. A unified monsoon index [J]. Geophys. Res. Lett., 29 (8): 115-1–115-4.

Li J P, Zeng Q C. 2003. A new monsoon index and the geographical distribution of the global monsoons [J]. Adv. Atmos. Sci., 20 (2): 299–302.

Li J P, Wang J X L. 2003. A new North Atlantic oscillation index and its variability [J]. Adv. Atmos. Sci., 20 (5): 661–676.

李建平, 任荣彩, 齐义泉, 等. 2013. 亚洲区域海—陆—气相互作用对全球和亚洲气候变化的作用研究进展 [J]. 大气科学, 37 (2): 518–538. Li Jianping, Ren Rongcai, Qi Yiquan, et al. 2013. Progress in air–land–sea interactions in Asia and their role in global and Asian climate change [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 37 (2): 518–538.

Li Y, Smith I. 2009. A statistical downscaling model for southern Australia winter rainfall [J]. J. Climate, 22 (5): 1142–1158.

Liu Z F, Xu Z X, Charles S P, et al. 2011. Evaluation of two statistical downscaling models for daily precipitation over an arid basin in China [J]. Int. J. Climatol., 31 (13): 2006–2020.

陆日宇. 2002. 华北汛期降水量变化中年代际和年际尺度的分离 [J]. 大气科学, 26 (5): 611–624. Lu Riyu. 2002. Separation of interannual and interdecadal variations of rainfall in North China [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 26(5): 611–624.

Nan S L, Li J P, Yuan X J, et al. 2009. Boreal spring Southern Hemisphere annular mode, Indian Ocean sea surface temperature, and East Asian summer monsoon [J]. J. Geophys. Res., 114 (D2): D2103.

Nicholas R E, Battisti D S. 2012. Empirical downscaling of high-resolution regional precipitation from large-scale reanalysis fields [J]. J. Appl. Meteor. Climatol., 51 (1): 100–114.

Pan L L. 2005. Observed positive feedback between the NAO and the North Atlantic SSTA tripole [J]. Geophys. Res. Lett., 32 (6): L06707.

Rayner N A, Parker D E, Horton E, et al. 2003. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century [J]. J. Geophys. Res., 108 (D14): 4407.

Sauter T, Venema V. 2011. Natural three-dimensional predictor domainsfor statistical precipitation downscaling [J]. J. Climate, 24 (23): 6132–6145.

Wu Z W, Wang B, Li J P, et al. 2009. An empirical seasonal prediction model of the East Asian summer monsoon using ENSO and NAO [J]. J. Geophys. Res., 114 (D18): D18120.

Wu Z W, Li J P, Jiang Z H, et al. 2012.Possible effects of the North Atlantic Oscillation on the strengthening relationship between the East Asian summer monsoon and ENSO [J]. Int. J. Climatol., 32 (5): 794–800.

Xia J, Zhang L, Liu C M, et al. 2007. Towards better water security in North China [J]. Water Resour. Manage., 21 (1): 233–247.

Yarnal B, Comrie A C, Frakes B, et al. 2001. Developments and prospects in synoptic climatology [J]. Int. J. Climatol., 21 (15): 1923–1950.

赵声蓉, 宋正山. 1999. 华北汛期旱涝与中高纬大气环流异常 [J]. 高原气象, 18 (4): 535–540. Zhao Shengrong, Song Zhengshan. 1999. Floods and droughts in northern China and general circulation anomalies over middle and high latitudes [J]. Plateau Meteor. (in Chinese), 18(4): 535– 540.

郑菲, 李建平. 2013. 前冬南半球环状模对春季华南降水的影响及其机理 [J]. 地球物理学报, 55 (11): 3542–3557. Zheng Fei, Li Jianping. 2012. Impact of preceding boreal winter Southern Hemisphere annular mode on spring precipitation over South China and related mechanism [J]. Chinese J. Geophys. (in Chinese), 55 (11): 3542–3557.

阮成卿, 李建平. 2016. 华北汛期降水分离时间尺度降尺度预测模型的改进 [J]. 大气科学, 40 (1): 215–226. Ruan Chengqing, Li Jianping. 2016. An improvement in a time-scale decomposition statistical downscaling prediction model for summer rainfall over North China [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 40 (1): 215–226, doi:10.3878/j.issn.1006-9895.1503.14317.

通讯作者李建平，E-mail: ljp@bnu.edu.cn

作者简介阮成卿，男，1987年出生，博士研究生，主要从事气候变化、气候预测方面的研究。E-mail: ruanchq@lasg.iap.ac.cn

收稿日期2014-11-16；网络预出版日期 2015-04-01

doi:10.3878/j.issn.1006-9895.1503.14317

文章编号1006-9895(2016)01-0215-12

中图分类号P461

文献标识码A