大干扰电网功角失稳原因的解耦鉴别分析方法

刘翔宇，梁纪峰，胡文平，胡雪凯，马慧卓

(国网河北省电力公司电力科学研究院，石家庄　050021)



大干扰电网功角失稳原因的解耦鉴别分析方法

刘翔宇，梁纪峰，胡文平，胡雪凯，马慧卓

(国网河北省电力公司电力科学研究院，石家庄050021)

摘要：针对大干扰电网稳定鉴别具体问题，提出一种应用解耦仿真分析鉴别功角稳定失稳主要诱因的方法，介绍该方法在典型故障案例中的实施过程，通过结论分析验证了该方法的正确性。

关键词：解耦仿真；功角稳定；大干扰；大电网

0引言

电网功角稳定可分为静态稳定、暂态稳定、小干扰动态稳定和大干扰动态稳定[1]。不同的稳定极限受不同因素影响，每一种电力系统失稳形式都存在主要诱因[2-3]，电力系统机电暂态过程中，对电力系统失稳模式的判别有时比较困难[3]，电压稳定和功角稳定往往联系紧密，难以区分[4-7]。

文献[8-9]对电力系统电压和频率稳定问题进行了分析，研究了影响稳定的因素，文献[10-12]研究了功角稳定问题下静稳极限和暂稳极限的快速求取问题。文献[13]通过发电机矩阵和负荷矩阵的概念，实现对负荷节点功角裕度和电压裕度计算，但方法并不适用大电网互联系统。现有文献中均未涉及功角稳定细化鉴别分析研究。

目前，在电网出现严重故障而迅速(第1或第2个振荡周期)失去稳定时，往往需要花费大量时间进行离线计算来确定主要诱因，且难以给出清晰、直观的分析鉴定结果。因此，针对电网失去稳定问题提出一种快速直观的鉴别分析方法。

1典型问题的提出

某年山西北部电网冬季运行方式下，山西北部500 kV电网通过雁同-神头和大同-房山2个输电通道与主网相连，由雁同-神头双回线向山西南部电网输送功率2 097 MW，由大同-房山三回线路向京津唐网输送功率4 656 MW。此时特高压线路长治-南阳向南输送功率5 000 MW，如图1所示。

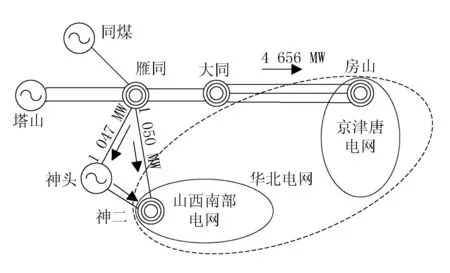
图1　山西北部500 kV电网结构

雁同-神头线路雁同侧发生单回线路三相短路N-2故障时，保护动作0.09 s跳开故障侧，0.1 s双回线路双侧跳开。保护动作后，山西北部电网迅速失去功角同步稳定，如图2所示。

图2　山西北部电网故障失稳情况

故障后山西北部电网受以下何种稳定极限限制失去同步稳定有待确定：雁同-神头双回断开后潮流转移超过大同-房山通道静稳极限；短路冲击超过了机电调节性能调节能力造成暂态失稳；故障激发了电网动态非周期失稳。

2静态暂态稳定极限分析

2.1静态稳定分析

图3为区域电网互联的等值系统图，对于高压大电网系统略去电阻，2个区域电网分别等值为发电机。2个系统间功率输送量。

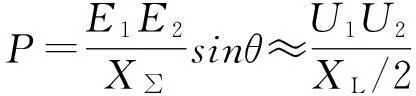
(1)

式中：Xs1和Xs2为系统等值电抗；U1和U2为区域电网的边界电压；XL为两区域电网间输电线路的电抗大小；X∑=Xs1+Xs2+XL/2；θ为2个发电机间的相角差；φ为U1和U2间相角差。

图3　区域电网互联等值系统图

正常运行时，系统运行在相对稳定的电压下，U1和U2大小变化不大，系统间功率输送极限主要决定于电气距离X∑。电网结构确定时X∑为确定值，如果强行增大此通道的输电容量，则θ增大，当θ大于90°，则系统失稳。

2.2暂态稳定分析

由式(1)可知，短路冲击引起的功角失稳原因为短路U1、U2点电压瞬间降低，则有功功率输送量Pe(1)瞬间变小为Pe(2)，此时各发电厂的机械转矩不能突变，则PM>Pe(2)，发电机获得加速转矩，转速增加。故障切除后Pe(3)>PM，发电机获得减速转矩，转速降低。在励磁系统强励作用下电压U1、U2将迅速增大以提升传输功率Pe，快关气门迅速动作使PM迅速减小，如迅速动作不能抵消短路冲击影响，加速面积abcd仍然大于减速面积edu，则造成失稳，如图4所示。

图4　单机无穷大系统功角特性曲线

3仿真鉴别方法的提出

3.1鉴别分析

要鉴别故障后失去功角稳定的主要原因，关键在于鉴别引起失稳原因在于短路冲击(过低的电压超出发电机机电调节水平)，还是电气距离过大(故障后输电阻抗变大)，使潮流转移后的输电通道的静稳极限小于的所需输送能力，进行的仿真鉴别如下：

仿真1：原方式下在雁同侧设置雁同-神头双回断线故障仿真，使山西北网与华北网联系由两通道变为单通道，增大电气距离，基本未改变电压，检验系统稳定性。

仿真2：在雁同-神头设置原N-2故障，故障后立即改变线路参数，减小大同-房山通道的电气距离，使大同-房山通道电气距离小于故障前，检验系统是否失稳。

可使大同-房山通道参数改变后电气距离X′小于故障前雁同-神头电气距离X(1)和大同-房山通道电气距离X(2)的并列值，即令

(2)

为了保障仿真2中短路冲击效果与原故障形式一致，以使机组机电调节作用不变，可通过在短路点设定短路阻抗形式限制故障点电压与原故障大致相同。

如果仿真1失稳，则在没有短路冲击作用下，故障后电网本身的强度已经不足以输送所需功率，超过故障后静稳极限成为导致电网失稳的原因；如果仿真2失稳则说明在输送通道存在较大冗余的情况下，电网在短路冲击作用下失去稳定，事故暂态冲击成为导致失稳的原因。

3.2算法流程

算法流程如图5所示。

图5　功角失稳鉴别算法流程

a. 将电网发生的故障K造成故障点D及电网电压下降和电网切除故障时拓扑结构由G改变为T两方面影响因素独立考虑。

b. 考虑以下故障仿真，仿真1：用断线故障模拟故障后的电网拓扑结构由G变为T的影响因素；仿真2：原故障基础上限制故障点D电压，模拟故障点电压下降因素，同时补偿电气距离变大因素。

c. 分别计算仿真1和仿真2的稳定情况，判别电网是否能够保持同步稳定。

d. 基于步骤c的稳定判别结果，对电网发生故障K造成失去稳定同步的原因作出如下鉴别。

情况1：仿真1失稳，仿真2不失稳，故障K造成的电网失稳，主要由于故障后，电网结构改变，达到静态稳定极限限制。

情况2：仿真1失稳，仿真2失稳，故障K造成的电网失稳，由于故障达到暂态稳定限制和故障后电网达到静态稳定极限限制共同作用，并且两个原因皆可单独造成电网失去稳定。

情况3：仿真1不失稳，仿真2失稳，故障K造成的电网失稳，主要由于故障达到暂态稳定限制原因。

情况4：仿真1不失稳，仿真2不失稳，故障K造成的电网失稳，由暂态稳定和故障后静态稳定极限限制合力作用造成，是静稳问题和暂稳问题相互影响产生，亦可考虑非周期动态失稳原因。

3.3仿真计算结果

应用电力系统计算分析软件PSD-BPA对模拟故障进行分析。

3.3.1仿真1的计算鉴别

操作设置：对雁同-神头进行断线故障仿真。

操作结果：系统功角失稳。

选取具有代表性的仿真曲线展示仿真失稳结果如图6所示。

图6　仿真1计算结果

3.3.2仿真2的计算鉴别

操作设置：对雁同-神头进行原故障仿真，在故障后0.12 s改变大同-房山通道线路的参数，令k=0.5用式(2)求取大同-房山新的电气距离。在0.12 s时在雁同点设置接地短路阻抗，保持其电压在较低水平(与N-2短路操作中对应时刻相当)。

操作结果：系统稳定。

选取具有代表性的仿真曲线展示仿真结果如图7所示。

图7　仿真2计算结果

4结果分析与讨论

仿真1中，断线故障不会造成明显电压改变，只会增大X∑，与原故障相比U1和U2未变小，而X∑不变，断开线路后潮流转移，系统功角失稳。即无短路冲击影响时，如果输电通道不拓宽，则系统失稳。

仿真2中，改变输电通道电气距离，使之大致小于原输电通道电气距离后，其静稳极限被增大，如图8所示，即使故障期间电压大小一直低于原N-2故障方式下，系统仍然能够保持稳定。即有短路冲击，但拓宽输电通道，系统仍稳定。

图8　雁同电压对比

综合以上2个验证算例的结果，认为造成稳定问题的主要原因为：故障后切除雁同-神头双回线路，潮流转移达到大同-房山通道静稳极限限制，而短路冲击过程拉低了电压，也在一定程度上加剧了失稳的过程。

另外，对大同-房山通道利用各种工程实用算法求取的静稳极限计算结果为6 770～7 000 MW，N-2后潮流转移，大同-房山线应承担的输送容量为6 724 MW左右，已经逼近静稳极限。由于故障后的波动，促使输送容量超过静稳极限。对静稳极限的计算一定程度上验证了以上的分析，山西省后续项目研究结果亦证明了结论的正确性。

5结束语

阐释了静态稳定问题和暂态稳定问题的实质，并对其限制影响因素进行分析，提出了通过仿真计算的方式单独考虑电压影响因素和电网拓扑结构影响因素从而实现判别和鉴定，方法应用的结果验证了鉴别方法的正确性，该方法具有计算量小，理论性强，结论清晰直观，易于利用商用软件(PSD-BPA等仿真软件)实现等特点。

参考文献：

[1]DL 755—2001，电力系统安全稳定导则[S]．

[2]孙华东，汤涌，马世英.电力系统稳定的定义与分类述评[J]，电网技术，2006，30(17)：31-35．

[3]汤涌，林伟芳，孙华东，等．基于戴维南等值跟踪的电压失稳和功角失稳的判别方法[J]．中国电机工程学报，2009，29(25)：1-6．

[4]何大愚．对于美国西部电力系统1996年7月2日大停电事故的初步认识[J]，电网技术，1996，20(9)：35-39．

[5]刘光晔，杨以涵．电力系统电压稳定与功角稳定的统一分析原理[J]．中国电机工程学报，2012，33(13)：135-149．

[6]张靖，文劲宇，程时杰，等．基于向量场正规形的电力系统稳定模式相关性理论分析[J]．中国电机工程学报，2006，26(11)：82-86．

[7]范强，彭志炜，张靖．功角稳定与电压稳定的关联性研究现状与展望[J]．电力系统保护与控制，2012，40(12)：41-48，55．

[8]汤涌，仲悟之，孙华东，等．电力系统电压稳定机理研究[J]．电网技术，2010，34(4)：24-29．

[9]孙艳，李如琦，孙志媛．快速评估电力系统频率稳定性的方法[J]．电网技术，2009，33(18)：73-77．

[10]张文朝，何玉龙，顾雪平，等．单输电通道中输电断面静稳极限的快速估算[J]，电网技术，2012，36(5)：92-95．

[11]李岳．暂态稳定约束的极限传输能力的快速求取方法研究[D]．华北电力大学(保定)，2010．

[12]金敏杰，陈家荣，梅生伟，等．基于改进信号能量法估计暂态稳定极限[J]．中国电机工程学报，2004，24(9)： 1-6．

[13]韩文，韩祯祥．一种判别电力系统电压稳定和功角稳定的新方法[J]．中国电机工程学报，1997，17(6):367-368，376．

[14]中国电力科学研究院．PSD-BPA 暂态稳定程序用户手册(4.10版)[M]．北京：中国电力科学研究院，2008.

[15]国家电网公司．国家电网公司电力系统安全稳定计算规定[Z]．北京：国家电网公司，2006．

本文责任编辑：王洪娟

Decoupling Analysis on Identify Cause of Power Grid AngleInstability Under Large Disturbance

Liu Xiangyu,Liang Jifeng,Hu Wenping,Hu Xuekai,Ma Huizhuo

(State Grid Hebei Electric Power Research Institute,Shijiazhang 050021,China)

Abstract:Due to a large disturbance power grid angle stability identification problem, a method to identify the chief incentive of power-angle unstability by de-couple simulation analysis was proposed. The proposed method was expounded by operating procedure of a typical fault case, The results of application verified the correctness of the identification method.

Key words：decoupling simulation;angle instability;large disturbance;bulk power grid

中图分类号：TM712;TM743

文献标志码：A

文章编号：1001-9898(2016)01-0030-04

作者简介：刘翔宇(1987-)，男，工程师，主要从事电力系统动态仿真、分析与控制工作。

收稿日期：2015-09-14