基于分数阶的多支路油气悬架模型研究
2016-03-23张军伟陈思忠李洪彪杨波左霞万芳
张军伟 陈思忠 李洪彪 杨波 左霞 万芳 李辰


摘 要:基于流体力学理论和理想气体状态方程,建立油气悬架主要部件的模型,包括节流阀模型、溢流阀模型、蓄能器模型、油缸模型。根据系统中各部件的连通关系,建立多支路油气悬架整数阶模型。引入分数阶理论,建立多支路油气悬架分数阶模型,并将分数阶模型、整数阶模型与台架试验对比,验证了分数阶模型的正确性。通过改变分数阶阶次,观察系统阻尼力的变化规律,证明了分数阶模型在研究刚度及阻尼非一致性问题时的优势,为后续的多支路油气悬架阻尼非一致性问题的研究奠定了基础。
关键词:分数阶;多支路;油气悬架;模型;阶次影响
中图分类号:U463.33文献标文献标识码:A文献标DOI:10.3969/j.issn.2095-1469.2015.06.04
Abstract:The models had been built for major components of a hydropneumatic suspension system based on knowledge of hydromechanics and the equation of state for an ideal gas. According to the connection of components, the integer order model of multi-branch hydropneumatic suspension was built and then the fractional order model was built based on the fractional order theory. The feasibility and advantages of the fractional order theory were verified through the comparison of the bench tests on both models. The influence of change in fractional operators on the system characteristics was analyzed for the subsequent research on damping non-coincidence in multi-branch hydropneumatic suspension.
Key words:fractional order; multi-branch; hydropneumatic suspension; model; fractional influence
对于多轴重型车辆,行驶路况复杂恶劣,载荷变化较大,油气悬架以车高可调、连通平衡、刚度非线性等优越特性在多轴重型车辆领域越来越多地得到应用。
由于各种建模和分析方法都有其自身的特点和局限性,必须针对具体问题采用适当的方法对系统进行理论分析和参数识别。下面通过查阅文献整理出一些比较有代表性的研究。Koenraad根据油气独立悬架油缸的内部结构,提出利用有关物理定律建立油气悬架油缸初始模型 [1]。Joo在综合考虑气体多变过程、孔口紊流出流方程、库仑摩擦力、油液的可压缩性和缓冲限位块等非线性因素后,建立了油气悬架的非线性数学模型 [2]。Felez等人提出了一种建立多轴汽车起重机互连式油气悬架模型的方法——功率键合图法,指出在多轴起重机上油气悬架相比传统悬架具有诸多优势 [3]。Yousefi 等人提出一种通过低阶近似对油气悬架非线性模型进行线性化处理的方法,通过设计一个包括模型特征参数的状态空间,使状态变量及其导数的近似值均达到最小[4]。
分数阶微积分很早就已经被提出[5-7],分数阶微积分理论是研究任意阶数的微分积分特性及应用的数学理论,是整数阶微积分理论的延伸和推广。
油气悬架是一个多相介质的组合体,气体随温度的变化、油液粘度、油液可压缩性、外力的作用时间及加载历史等都会影响到油气悬架特性,这些特性十分符合粘弹性物质的特点。粘弹性材料的力学性质介于理想弹性体和牛顿流体之间,既表现出弹性,同时又具有粘性特性,其应力-应变响应依赖于时间和应变率,又与载荷和变形历史有关,即应力-应变具有记忆性。而分数阶粘弹性微积分模型可以用较少的参数来准确地描述大量复杂的粘弹性材料在广泛频率范围内的动力学特性[8-10]。
1 多支路油气悬架结构简介
用于四轴重型车辆的互连式油气悬架,其前两桥与后两桥结构相同,以一二桥的结构为例来说明。系统采用双腔油缸,上腔为环形腔,下腔为无杆腔。一桥与二桥的同侧油缸上下腔对应连通,同桥左右侧油缸交叉连通。压缩行程时,油缸下腔的油液经多条支路流向蓄能器和其它油缸。
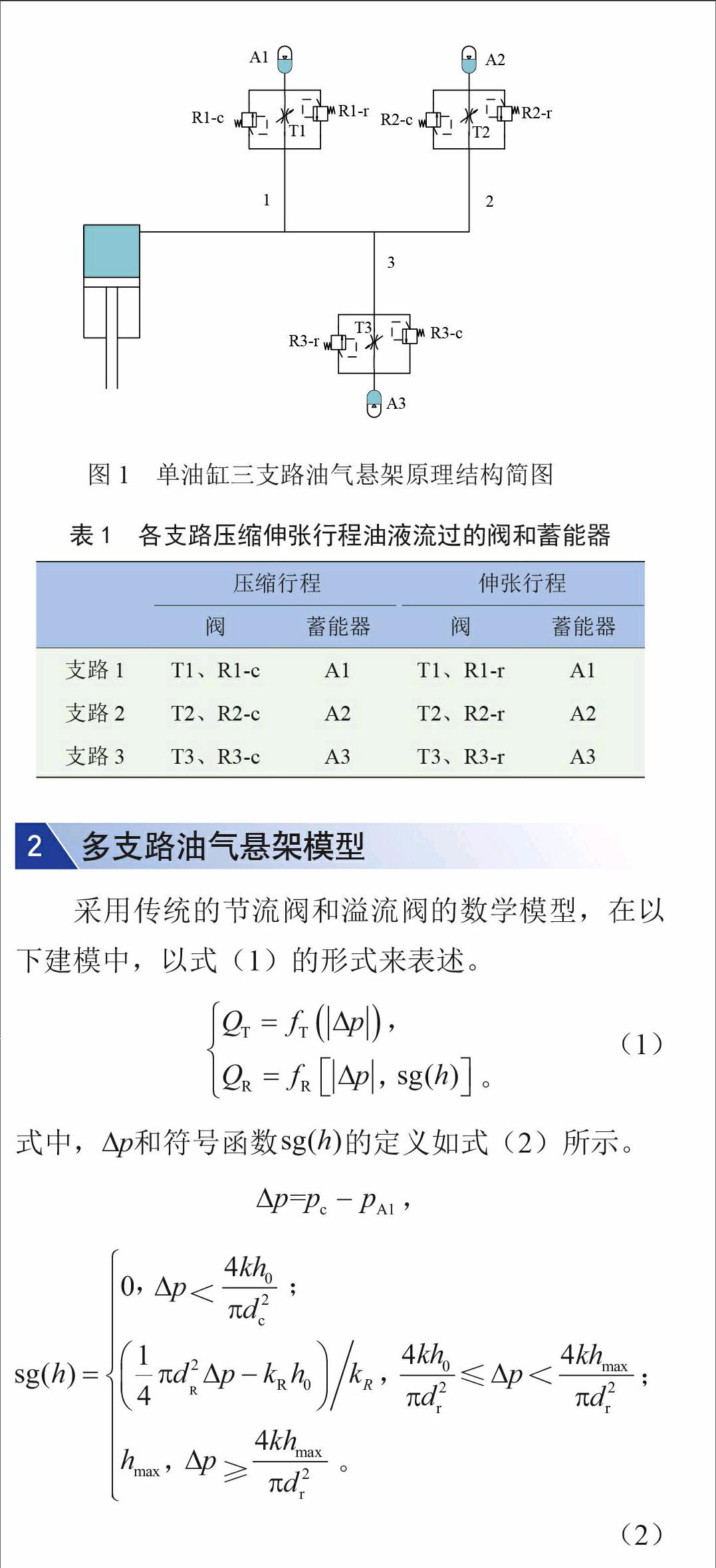
为了实现多轴车辆的轴荷平衡及抗侧倾功能,油气悬架的各油缸之间是按照一定的规则连通的,这就不可避免存在单个油缸连通多条支路的结构。以单油缸三支路结构的油气悬架为研究对象,对多支路油气悬架的建模方法进行研究,单油缸三支路油气悬架原理结构简图如图1所示。
一个单作用油缸分别通过三条支路与三个蓄能器连通,每条支路中包括节流阀、压缩溢流阀、伸张溢流阀。多支路油气悬架系统中三条支路压缩伸张行程油液所流过的阀见表1。
2 多支路油气悬架模型
采用传统的节流阀和溢流阀的数学模型,在以下建模中,以式(1)的形式来表述。
基于节流阀模型、溢流阀模型、蓄能器模型,可推导支路1数学模型如式(3)所示[11-12]。
式(1)~(4)中,QT1为支路1中节流阀T1的流量,m3/s;Q1为支路1总的流量,m3/s;dR1c为支路1中溢流阀R1-c的开口直径,m;为支路1中溢流阀R1-c的阀芯最大位移,m;dR1r为支路1中溢流阀R1-r的开口直径,m;为支路1中溢流阀R1-r的阀芯最大位移,m;pc为油缸内的压力,Pa;pA1为蓄能器A1内气体的压力,Pa。
同理得支路2和支路3的数学模型[13]。
由油缸内油液压力微分方程可得油缸模型如式(5)所示[14]。
式中,CHC为油缸的容积模量,m3/Pa;Vb为静平衡位置的油缸容积,m3;Koil为油液体积模量,Pa。
综合三条支路的模型和油缸模型,可得到单油缸多支路多蓄能油气悬架系统模型。基于已建立的节流阀模型、溢流阀模型、蓄能器模型、油缸模型,采用模块化建模方法,通过分析各部件模型之间的输入输出关系,建立多支路油气悬架系统建模流程图,如图2所示。各支路阀组模型输出的流量作为本支路蓄能器模型的输入,各支路蓄能器模型输出的压力和油缸模型输出的压力作为本支路阀组模型的输入,各阀组输出的流量作为油缸模型的输入。
3 多支路油气悬架分数阶模型
早先的学者对油气悬架弹性力和阻尼力的研究,是将系统看做理想的弹性体和流体,弹性力与位移之间满足一定的关系,阻尼力与速度之间满足一定的关系。但是,油气悬架是一个多相介质的组合体,既不是理想的弹性体也不是理想的流体,而是介于弹性体和流体之间的类似粘弹性体。因此,用分数阶微积分来描述油气悬架在广泛频率范围内的系统特性是恰当的。
3.1 分数阶微积分的定义及计算方法
分数阶微积分常见的有三种定义方式:Riemann-Liouville定义、Grunwald-Letnikov定义和Caputo定义,在工程应用中最常用到的是Riemann-Liouville定义。
Riemann-Liouville分数阶微分定义为
目前对分数阶微积分常用的计算方法中,滤波逼近的方法效果较好,精度理想,并且可以对位置的信号进行分数阶微积分,最具代表性的是由Oustaloup提出的滤波逼近分数阶的方法[15-16]。研究表明,当逼近阶次时,对不同的分数阶次α,无论是幅频特性还是相频特性,都能很好地逼近实际分数阶滤波器的频率特性[17]。
3.2 多支路油气悬架分数阶模型
鉴于油气悬架是一个多相介质的组合体,其特性不仅和外力大小有关,还和温度的改变、力的作用时间及加载历史都有关系,这些十分符合粘弹性物质的特点。基于以上分析,利用分数阶粘弹性微积分模型可以用较少的参数来准确地描述大量复杂粘弹性材料在广泛频率范围内动力学特性的优势,将油气悬架系统整体等效为粘弹性系统进行研究,引入分数阶模型描述弹性力和阻尼力项,建立油气悬架分数阶模型,对油气悬架系统输出力特性进行分析。
基于前面建立的多支路油气悬架整数阶模型,用分数阶算子替换已建立的整数阶模型中的位移项和速度项。观察整数阶模型的各方程,只有油缸模型的表达式中含有位移项和速度项,用分数阶算子替换表达式中的位移项和速度项之后,如式(8)所示,其它部分的模型保持不变。
4 多支路油气悬架分数阶模型仿真分析
4.1 分数阶阶次和传递函数的确定
对于Oustaloup滤波逼近法,当阶次时已经能满足精度和计算量的要求,因此采用五阶有理函数来逼近分数阶函数。考虑到车辆工作的有效频率范围,选取逼近频率区间为[0.01 rad/s,100 rad/s],即,,采用试错法找出阶次α和β的最优取值。阶次α和β取值与对应的五阶传递函数见表2。
4.2 分数阶模型与试验对比分析
仿真参数见表3。在1.0 Hz/0.03 m正弦激励下,经仿真对比,当分数阶模型中的阶次α-0.1、β0.9时,仿真曲线与试验曲线更接近,阻尼力仿真曲线与试验曲线对比如图3所示。
图3中黑色实线为试验测得的阻尼力曲线,红色虚线为整数阶模型仿真得到的阻尼力曲线,蓝色点画线为分数阶模型仿真得到的阻尼力曲线,由两条曲线对比可以看出,分数阶模型的仿真曲线,其原点左右两侧的曲线不对称性更明显,阻尼力最大值不在原点处取得,分数阶模型更能体现多支路油气悬架阻尼力的实际特性。
由分数阶模型仿真曲线和试验曲线的对比,证明了油气悬架分数阶模型的可行性和准确性,体现了分数阶的阶次可以任意连续可调的优势。
改变节流阀T1的节流孔直径,观察节流孔直径变化对分数阶模型的阻尼力-位移曲线、阻尼力-速度曲线的影响,验证油气悬架分数阶模型的参数灵敏度,如图4和图5所示。
图4为不同节流孔直径下的分数阶模型阻尼力-位移曲线,横轴的上半部分为压缩行程阻尼力曲线,从最低点-30 mm运动到最高点30 mm;下半部分为伸张行程阻尼力曲线,从最高点30 mm运动到最低点-30 mm。由图4可以看出,随着节流孔直径的减小,分数阶模型的阻尼力增大,且阻尼力曲线的左右非对称性变得更加明显,即压缩行程下半段(-30~0 mm)的阻尼力小于压缩行程上半段
(0~30 mm)的阻尼力,伸张行程上半段(30~0 mm)
的阻尼力小于伸张行程下半段(0~-30 mm)的阻尼力,即多支路油气悬架存在阻尼非一致性问题。
图5为不同节流孔直径下的分数阶模型阻尼力-速度曲线,第一象限为压缩行程阻尼力曲线,第三象限为伸张行程阻尼力曲线。由图5可知,随着节流孔直径的减小,分数阶模型的阻尼力增大,并且在一个完整压缩伸张行程中,阻尼力曲线不重合,中间有一定的包络面积,随着节流孔直径的减小,阻尼力曲线之间的包络面积逐渐增大,即多支路油气悬架的阻尼力非一致性问题变得更加显著。
4.3 分数阶节次对阻尼力的影响及物理意义
经前面的分数阶模型仿真与试验对比,验证了分数阶模型的可行性与正确性。分数阶的阶次对模型的幅值和相位会产生影响,给系统加入1.0 Hz/30 mm的正弦激励信号,分析分数阶的阶次对油缸活塞速度、阻尼力-时间曲线、阻尼力-位移曲线的影响,为分数阶模型的阶次选择提供理论指导,并结合油气悬架的实际情况,对分数阶的物理意义进行阐述。
图6为不同分数阶阶次下的阻尼力-时间曲线。由图6可知,当阻尼分数阶算子的阶次β=1.0时,阻尼力在相位上和油缸速度是同步的,幅值在七条曲线中居中,此种情况表征了油气悬架理想动态特性,即油气悬架的系统输出特性与油缸运动状态同步。
当阻尼分数阶算子的阶次β<1.0时,阻尼力在相位上相对油缸速度存在延迟,随着阶次的减小,相位延迟增大,阻尼力幅值逐渐减小,此种情况表征了油气悬架实际的动态特性,即油气悬架的系统输出特性与油缸运动状态存在相位延迟。在实际中由于油液可压缩性、油液受温度的影响、气体受温度的影响、管道压力损失、油缸与活塞的摩擦力等因素,阻尼力在相位上和油缸速度存在一定的延迟,且阻尼力幅值也会较理想情况有所减小,在[0, 1.0]区间内通过适当选取阶次,可以达到相位及幅值与实际情况较好吻合的效果。分数阶阶次的选取体现了油液可压缩性、油液受温度的影响、气体受温度的影响、管道压力损失等因素的综合影响效果。当阻尼分数阶算子的阶次β趋于0时,相位延迟达到90°,经仿真研究,阻尼分数阶算子的阶次在区间[0.8, 1.0]内选取能达到与实际情况较好吻合的效果。
当阶次β>1.0时,阻尼力在相位上相对油缸速度存在超前,随着阶次的增大,相位超前增大,阻尼力幅值逐渐增大。在实际中,油气悬架输出特性在相位上不会产生比油缸运动状态超前的情况,因此,此种情况没有实际的物理意义。
图7为不同分数阶阶次下的阻尼力-位移曲线,零点上方为压缩行程阻尼力曲线,零点下方为伸张行程阻尼力曲线。由图7可知,当阻尼分数阶算子的阶次β=1.0时,以位移零点为分界线的阻尼力曲线左右部分基本是对称的;当阶次β<1.0时,在位移绝对值相同位置处(例如,看图中位移为0.02 m和-0.02 m处),压缩行程左半部分曲线要比右半部分曲线幅值小,伸张行程左半部分曲线要比右半部分曲线幅值大,即左右部分的曲线是不对称的,且随着阶次的减小,这种不对称性变得更加明显;当阶次β>1.0时,没有明确的物理意义,这里就不再讨论。
图8为不同分数阶阶次下的阻尼力-速度曲线,零点上方为压缩行程阻尼力曲线,零点下方为伸张行程阻尼力曲线。当阶次β=1.0时,在一个完整的压缩和伸张行程,阻尼力-速度曲线重合为一条曲线;当阶次β<1.0时,在一个完整的压缩和伸张行程中,阻尼力-速度曲线不再重合为一条曲线,而是有一定的包络面积,且随着阶次的减小,包络面积逐渐增大,这就是多支路油气悬架阻尼非一致性问题,在后续的工作中将对其进行深入研究。
5 结论
根据系统结构,采用模块化的建模方法,建立了多支路油气悬架整数阶模型。针对油气悬架是多相介质组合体的特点,将油气悬架等效为粘弹性体,引入分数阶微积分理论,建立了多支路油气悬架分数阶模型。将模型仿真与台架试验对比,并进行了后续的分析,可得到以下结论:
(1) 通过分数阶模型仿真、整数阶模型仿真与台架试验的对比,证明了多支路油气悬架分数阶模型准确性更高,更能反映多支路油气悬架的实际特性。
(2) 改变节流孔直径的大小,观察多支路油气悬架阻尼力的变化,结果表明,系统阻尼力随节流孔直径变化的灵敏度是满足要求的。
(3) 改变分数阶阶次,当阻尼分数阶算子的阶次等于1时,表征了油气悬架理想动态特性,即油气悬架的系统输出特性与油缸运动状态同步;当阻尼分数阶算子的阶次小于1时,阻尼力在相位上相对油缸速度存在延迟,此种情况表征了油气悬架实际的动态特性,即油气悬架的系统输出特性与油缸运动状态存在相位延迟;当阻尼分数阶算子的阶次大于1时,阻尼力在相位上相对油缸速度存在超前,此种情况没有实际的物理意义。
参考文献(References):
KOENRAAD R. A Nonlinear Parametric Model of an Automotive Shock Absorber [C]// SAE Paper 940869.
JOO F R. Dynamic Analysis of a Hydro-pneumatic Suspension System [D]. Montreal:Concordia University,1991.
FELEZ J,VERA C. Bond Graph Assisted Models for Hydro-pneumatic Suspensions in Crane Vehicles [J]. Vehicle System Dynamics,1987,16(5-6):313-332.
YOUSEFI A,BORIS S. Order Reduction of Nonlinear Hydro-pneumatic Vehicle Suspension [C]//Proceedings of the 2006 IEEE International Conference on Control Applications,Munich,2006,1404-1408.
LEIBNIZ G W. Mathematical Schiften [M]. Hildeshcim:Olms Verlagsbuchhandlung,1962.
OLDHAM K B,SPANIER J. The Fractional Calculus [M]. New York:Academic Press,1974.
MANDELBROT B B. The Fractal Geometry of Nature [M]. New York:W. H. Freeman and Company,1982.
孙会来,金纯,张文明,等. 工程车辆油气悬架分数阶建模与特性分析 [J]. 农业机械学报,2014,45(5):16-21.
Sun Huilai,Jin Chun,Zhang Wenming. Fractional Modeling and Characteristic Analysis of Hydro-Pneumatic Suspension for Construction Vehicle [J]. Transactions of the Chinese Society for Agricultural Machinery,2014, 45(5):16-21.(in Chinese)
朱呈祥,邹云. 分数阶控制研究综述 [J]. 控制与决策, 2009,24(2):161-169.
Zhu Chengxiang,Zou Yun. Summary of Research on Fractional-Order Control [J]. Control and Decision, 2009,24(2):161-169. (in Chinese)
吴光强,黄焕军,叶光湖. 基于分数阶微积分的汽车空气悬架半主动控制[J]. 农业机械学报,2014,45(7):19-25.
Wu Guangqiang,Huang Huanjun,Ye Guanghu. Semi-Active Control of Automotive Air Suspension Based on Fractional Calculus [J]. Transactions of the Chinese Society for Agricultural Machinery,2014,45(7):15-22. (in Chinese)
Zhang Junwei,Chen Sizhong,Yang Lin. Research on Nonlinear Stiffness Characteristics of Hydro-Pneumatic Spring [J]. Applied Mechanics and Material,2012 (128-129):421-425.
张军伟,陈思忠,吴志成. 刚度和阻尼均可调的油气悬架设计与试验 [J]. 汽车工程学报,2013,3(2):106 -112.
Zhang Junwei,Chen Sizhong,Wu Zhicheng. Design and
Test of a Hydro-Pneumatic Suspension with Adjustable Stiff-ness and Damping,2013,3(2):106 -112. (in Chinese)
张军伟. 多轴重型车辆互连式油气悬架系统特性研究 [D]. 北京:北京理工大学,2015.
Zhang Junwei. Research on System Characteristics of Interconnected Hydro-Pneumatic Suspension for Multi-axle Heavy Vehicle [D]. Beijing:Beijing Institute of Technology,2015. (in Chinese)
Zhang Junwei,Chen Sizhong. Modeling and Study on Active Vibration Control of an Off-Road Vehicle [J]. Vehicle System Dynamics,2014,52(5):581-607.
OUSTALOUP A,LEVRON F,MATHIEU B. Frequency Band Complex Noninteger differentiator:Characterization and Synthesis [J]. IEEE Transactions on Circuit and Sys-temsⅠ,Fundamental Theory and Applications,2000,47(1):25-39.
Chen Y. A New Discretization Method for Fractional Order
Differentiators via Continued Fraction Equation [C]//2003 ASME International Design Engineering Technical Con-ferences,September 2-6,Chicago,2003:1-9.
NEWMAN D J. Rational Approximation to [J]. Michigan Mathematical Journal,1964 (11):11-14.
