扩散型梯形断面跃后共轭水深的解析计算研究
2016-03-22浙江省水利水电勘测设计院杭州310002
黄 朝 煊(浙江省水利水电勘测设计院,杭州 310002)
0 引 言
随着国家对农田水利发展的重视以及“五水共治”的提出,水闸消能计算显得尤为重要。针对现有水闸消能计算公式只适用于矩形翼墙断面,而实际工程设计中也有采用梯形翼墙断面情况,如文献[1]中舟山市六横小郭巨围垦工程挡潮排涝闸,由于外海潮位不停变化,通常矩形闸门内外水压波动,闸门周边橡皮止水水封不密实,渗漏很严重,因此,设计单位创新性的提出了梯形闸门,该型闸门水密性很好,可完全解决挡潮排涝闸的渗漏问题。基于此,本文对扩散型梯形断面水跃计算进行了深入研究。
《水闸设计规范》[2]对水闸消能计算的研究仅针对矩形断面的,对于工程实际中的梯形翼墙断面消能计算,往往采用矩形断面进行面积等效转换,该近似等效法误差较大,影响工程实际消能防冲安全。黄朝煊[3]对矩形断面消力池池深极值进行了无量纲化数学推导,得出了矩形断面消力池池深极值的直接计算公式。王贺瑶等[4]对考虑底挑离心力时的收缩水深计算进行了深入研究,并给出了直接解析计算式。李蕊等[5]、刘玲等[6]、张志昌等[7]分别给出了棱柱体梯形断面跃后共轭水深计算得迭代算法,计算较复杂;刘计良等[8]给出了近似拟合算式,但局部计算区间误差较大。文献[9]、[10]采用智能算法对消能进行了研究,但无法寻找本质共性特征。
王正中等[11]、黄朝煊[12,13]对梯形断面临界水深、收缩水深等特征水深进行了深入研究,为扩散型梯形断面共轭水深的计算提高了基础。
鉴于当前对水闸消力池计算仅适用于矩形断面,本文将通过数学分析理论,结合Matlab软件及CurveExpert软件对扩散型梯形翼墙断面共轭水深计算进行深入研究。
1 跃前收缩水深的解析算式
收缩水深方程为:
(1)
式中:T0为以收缩断面底部为基准面的泄水建筑物上游总水头,m;h1为收缩断面水深,m;g为重力加速度常数;φ为流速系数;A1为收缩断面过水面积,m2;q为过闸单宽流量,m3/(s·m),见图1、2。
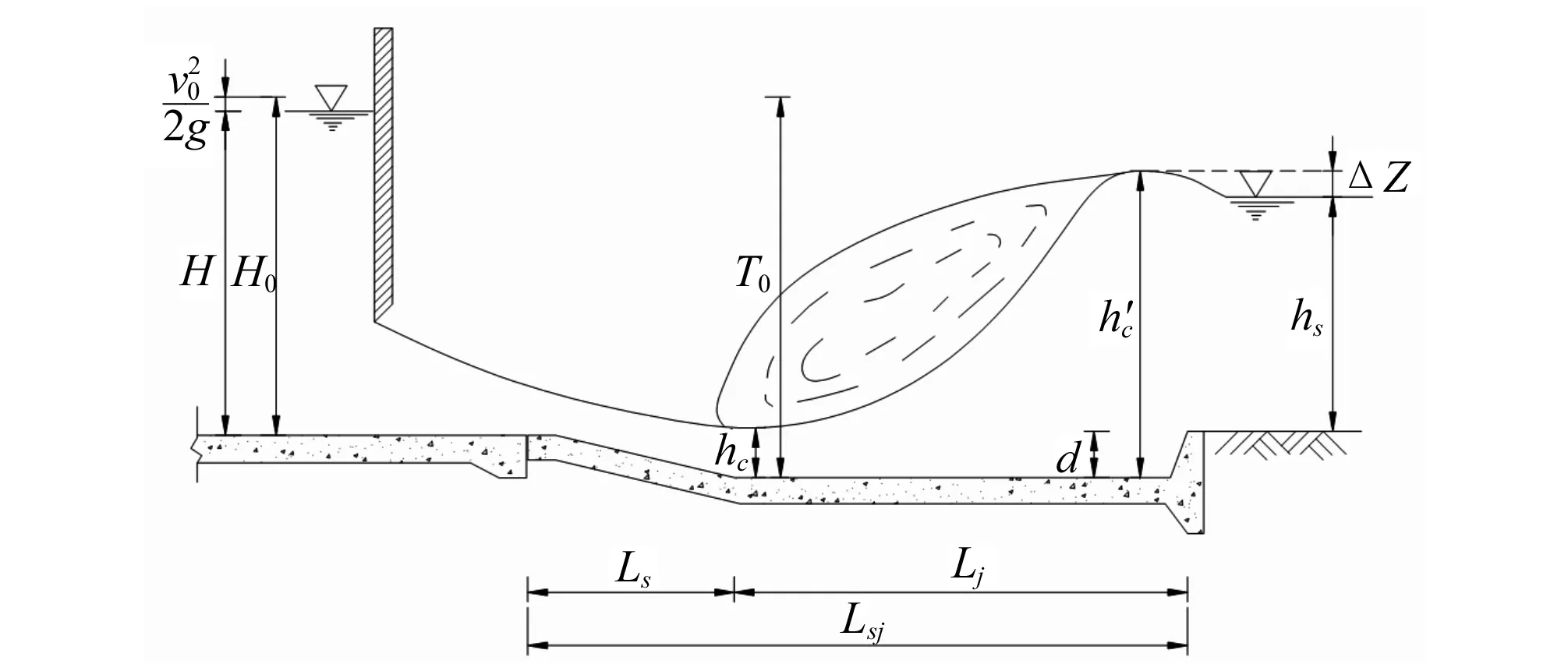
图1 水闸消力池消能简图
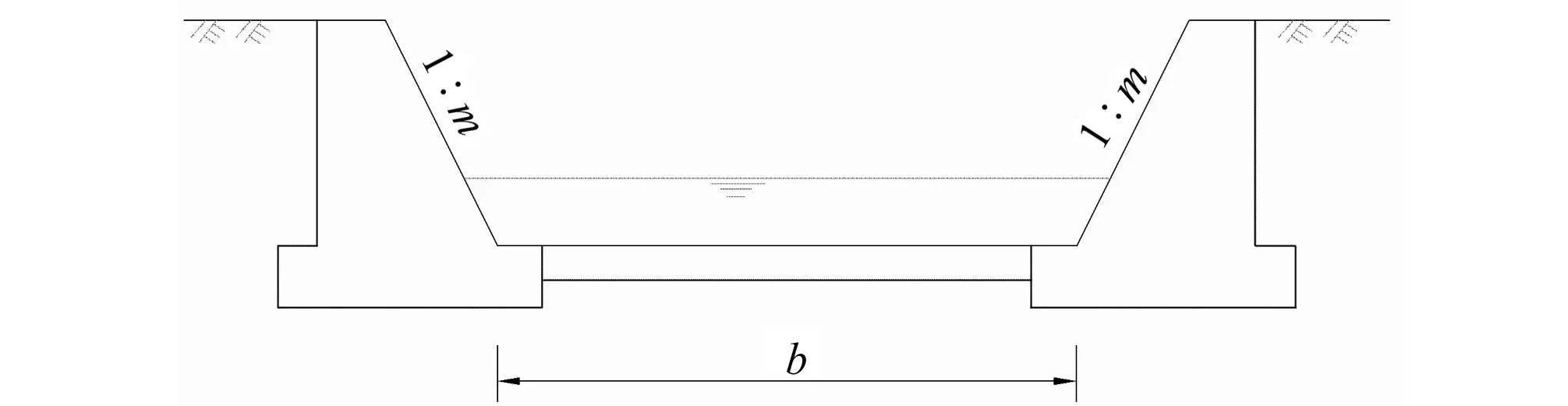
图2 消力池梯形翼墙断面简图
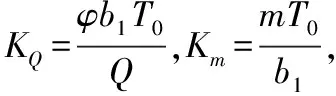
(2)
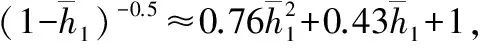
将以上高精度等效计算式代入公式(2)可知:
(3)
求解一元二次方程(3)可知:
(4)
通过大量数值计算研究,本文收缩水深计算公式(4)最大相对误差<0.5%(见图4),精度完全满足工程计算要求。为了更直观的反应收缩水深h1/T0与无量纲KQ、Km关系,通过数值计算得关系曲面图5。
当断面坡比影响参数Km=0时,便退化为水闸设计规范(SL265-2001)附录中矩形断面的收缩水深计算公式B1.1.1-3,可见该计算公式是本文公式(4)的特例。
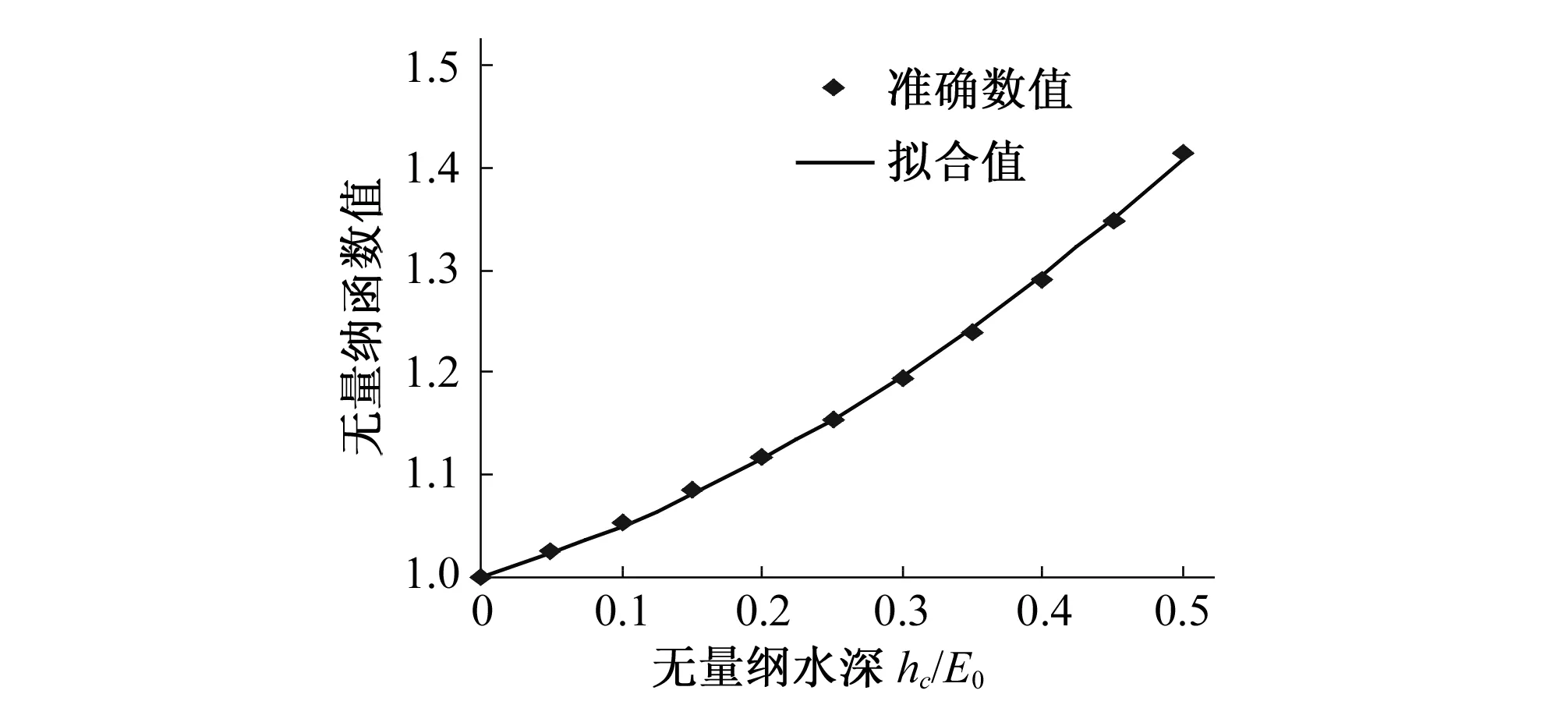
图3 函数高精度二次曲线拟合
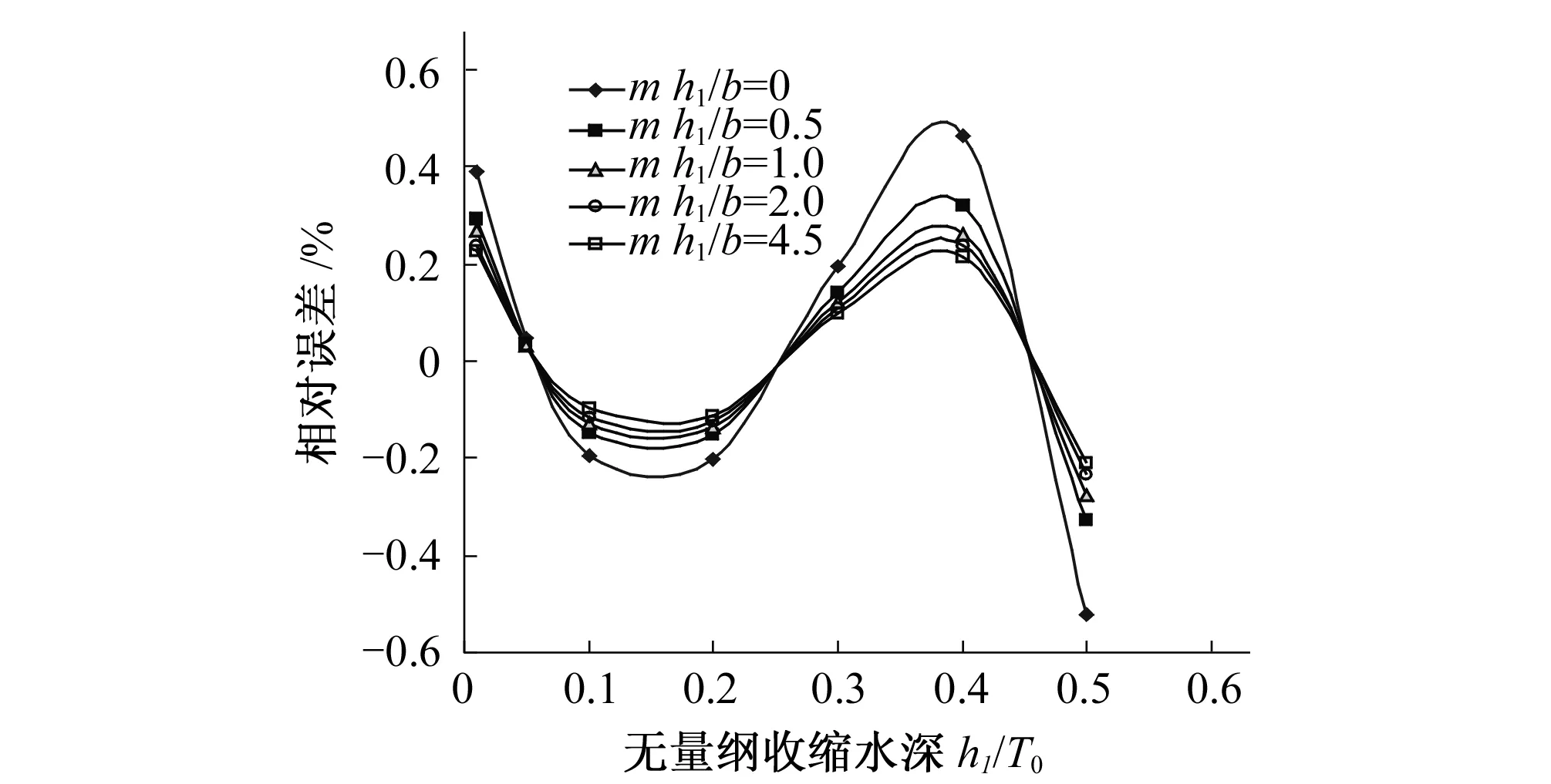
图4 公式(4)相对误差分布曲线图
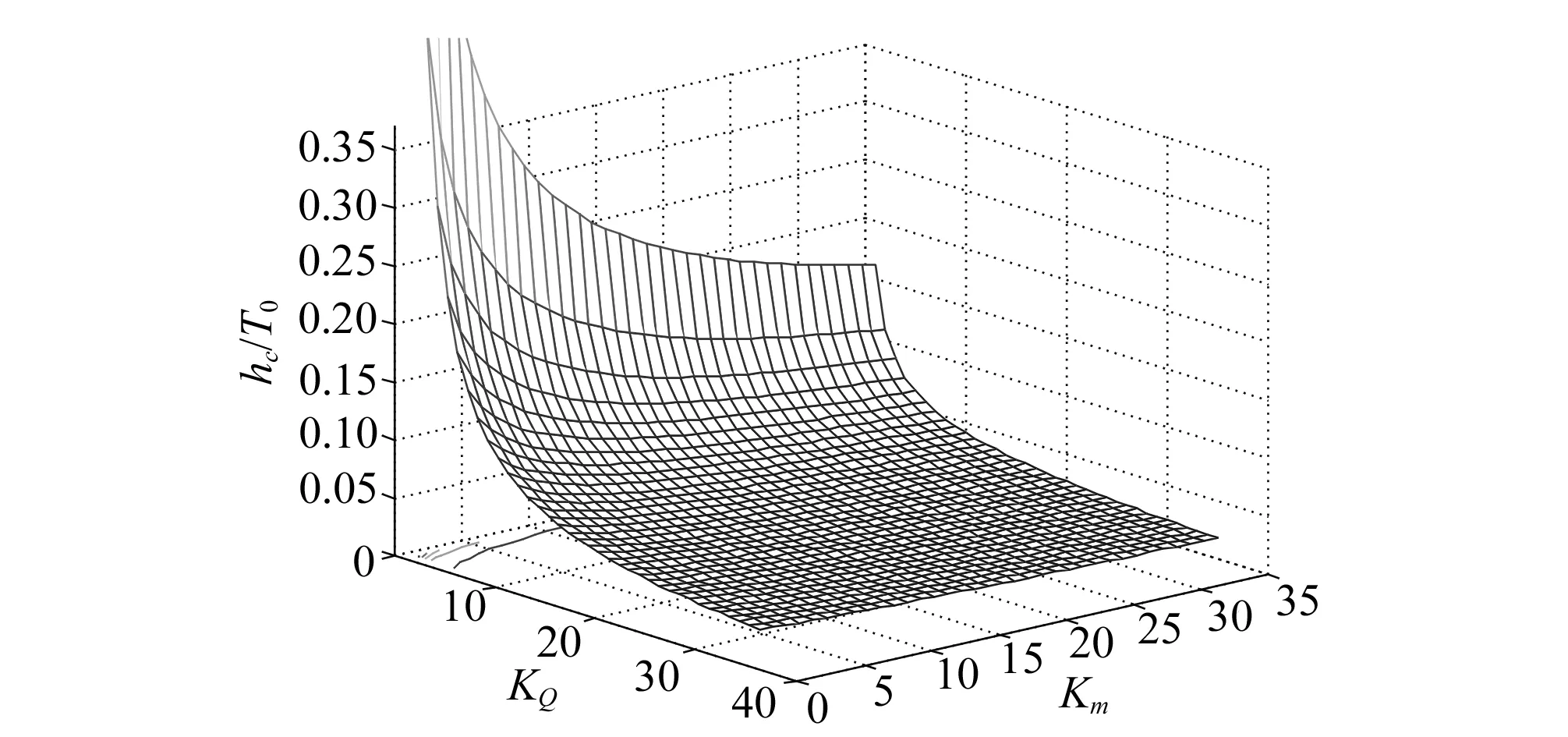
图5 h1/T0与无量纲KQ、Km关系曲面
2 跃后共轭水深计算
对于扩散型梯形翼墙断面下水跃共轭水深的计算,利用连续方程和动量方程推导得水跃方程为:
(5)
式中:v1、v2为跃前断面和跃后断面平均流速;g为重力加速度;α1、α2为跃前断面和跃后断面流速系数;F1、F2为跃前断面和跃后断面顺水流轴线方向作用力;F3为扩散段翼墙水压力在顺水流轴线方向的投影分量值。
根据水压力计算理论可知(见图6):
(6)
F3计算考虑水跃过程中水面线的非线性变化的影响,将公式(6)代入公式(5)可得:
(7)
其中参数ε为水跃过程中水面线的非线性变化的影响系数,一般1≤ε<1.2,本文近似取ε=1;m1、m2为跃前断面和跃后翼墙断面坡比,取m1=m2=m,取α1=α2=1,记η2=mh2/b2,η1=mh1/b1,ξ=b1/b2。
将以上参数代入方程(7)可知:
(8)
公式(8)即为跃后共轭水深的计算方程,该方程也是一元五次方程,一般情况下无法得出公式解。
2.1 无扩散时(ξ=1)跃后共轭水深的一元四次方程公式解
对无扩散时梯形断面共轭水深计算,刘计良等[10]中给出了近似计算法,但精度不高,其中最大跃后水深相对误差甚至大于5%。本文将根据数学方程理论,求出跃后共轭水深精确解析解。
对于无扩散情形,即b1=b2=b时,ξ=1,公式(8)可进一步简化为:
(9)
易知公式(9)是对称方程,η1、η2均是一元五次对称方程(9)的实根,由水跃前收缩水深计算水跃后共轭水深时,可将对称方程(9)除以(η2-η1)进而转化为一元四次方程,便能求出其解析公式解。
记K0=Q2m3/(gb5),设跃前收缩水深无量纲值η1,跃后水深无量纲值η2为待求量,设t=η2-η1,代入公式(9)变换后得:
(t+η1)3[2t+(2η1+3)][t+(η1+1)]+6K0=
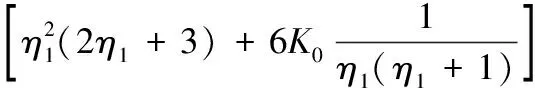
(10)
以上对称方程满足初始条件,η2=η1(即t=η2-η1=0)是方程(10)的一个特解,以上关于t=η2-η1的五次方程常数项为0;方程两边同除以t,即以上方程转化为四次方程:
t4+a1t3+a2t2+a3t+a4=0
(11)
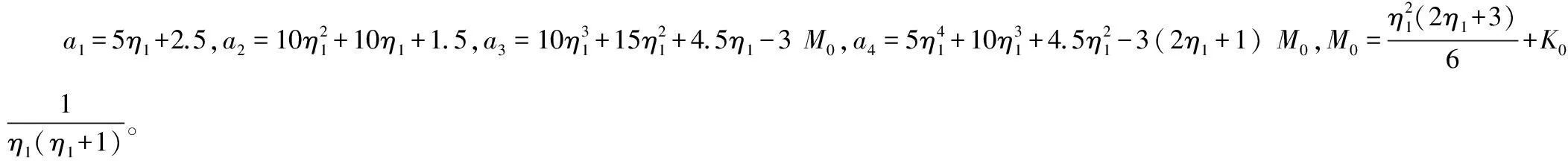
根据代数方程根的判别式理论,易知以上四次方程(11)含有一对复数根(实部为负)、一正实根(待求共轭水深)以及一个负实根。
通过变量参数变换,设z=t+a1/4,方程(11)可以转化为三次项系数为0的四次等价方程:
z4+c2z2+c3z+c4=0
(12)
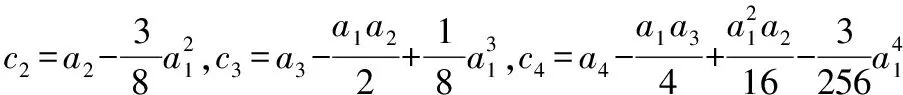
z4+c2z2+c3z+c4=(z2+kz+d1)(z2-kz+d2)
(13)
通过对待定系数法各项系数的恒等关系消元变换得,待定系数k2满足以下的三次方程:
(k2)3+2c2(k2)2+(c22-4c4)k2-c23=0
(14)
利用卡当公式解求解方程(14),可得待定系数k2的正实根为:
(15)
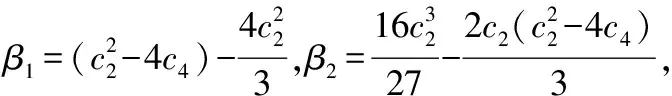
将k2代入方程(13)右边的因式分解项,故方程(13)降次为两个一元二次方程,求解得正根z:
(16)
根据上文参数代换z=t+a1/4;t=η2-η1,求解得跃后共轭水深的精确解析计算式为:
(17)
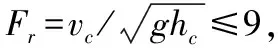
根据以上解析法可求出水跃相对共轭水深x、y随无量纲参数K0之间的精确数据关系表,见表1,通过分析可知,当0.2
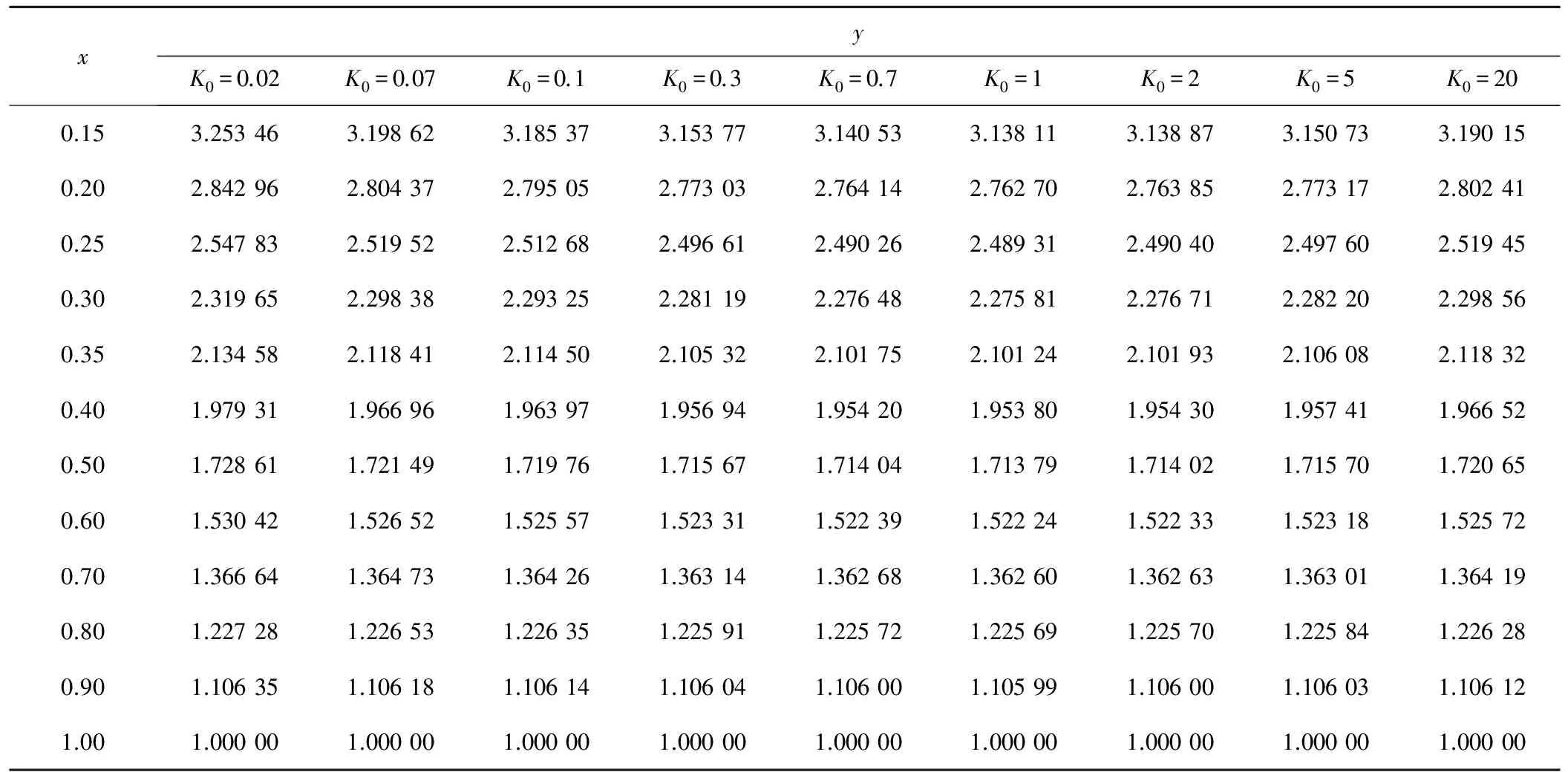
表1 依据共轭水深公式解求出的精确共轭水深x~y~K0关系表
通过数学理论推导及最佳逼近拟合原理,得出无扩散时(ξ=1)共轭水深的简洁近似计算公式:
(18)
2.2 扩散型(0.5<ξ<1)跃后共轭水深计算
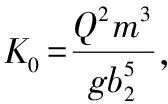
(19)
方程(19)为关于η2的一元五次方程,其中无量纲参数K0、η1、ξ均为已知参数。
由于方程(19)较复杂,无法直接求解,可采用迭代法求解,其迭代方程由方程(19)变换而得,其形式如下:
(20)
通过对公式(20)右边求导容易证明其导数绝对值小于1,即迭代方程(20)收敛,限于篇幅,本文未详细给出证明。
其迭代初值可根据无扩散时(ξ=1)跃后共轭水深的修正值(乘以修正系数ξ)给出,公式如下:
(21)
其中收缩断面的临界水深无量纲值可通过以下公式计算(见黄朝煊[12]):
η1k=0.5[1+3.952λ(1+4λ)0.202 5]0.5-0.5
(22)
通过Matlab软件大量数值计算分析可知,本文初值公式(21)精度较好,最大相对误差一般小于5%,通过迭代公式(20)迭代一次后精度基本小于1.0%,满足工程实际计算要求。
2.3 扩散型(0.5<ξ<1)跃后共轭水深的数值分析研究
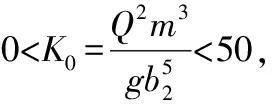
(23)
即比值函数H(x,K0, ξ)为跃后水深初值公式(21)与精确值的比值关系,其反应跃后水深初值公式的误差大小,H(x,K0, ξ)=1则表示跃后水深初值与精确值一致,相对误差为0;H(x,K0, ξ)=0.9则表示跃后水深初值相对误差为-10%;同理,H(x,K0, ξ)=1.1则表示跃后水深初值相对误差为10%。
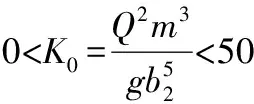
由图7可知,本文跃后水深初值公式(21)在一般情况下精度还是比较高的,只是在K0较小(小于0.2)时相对较敏感,误差稍大;迭代公式(20)收敛速度较好,一般迭代一次后便能得出精度较高的解,完全满足工程实践要求。
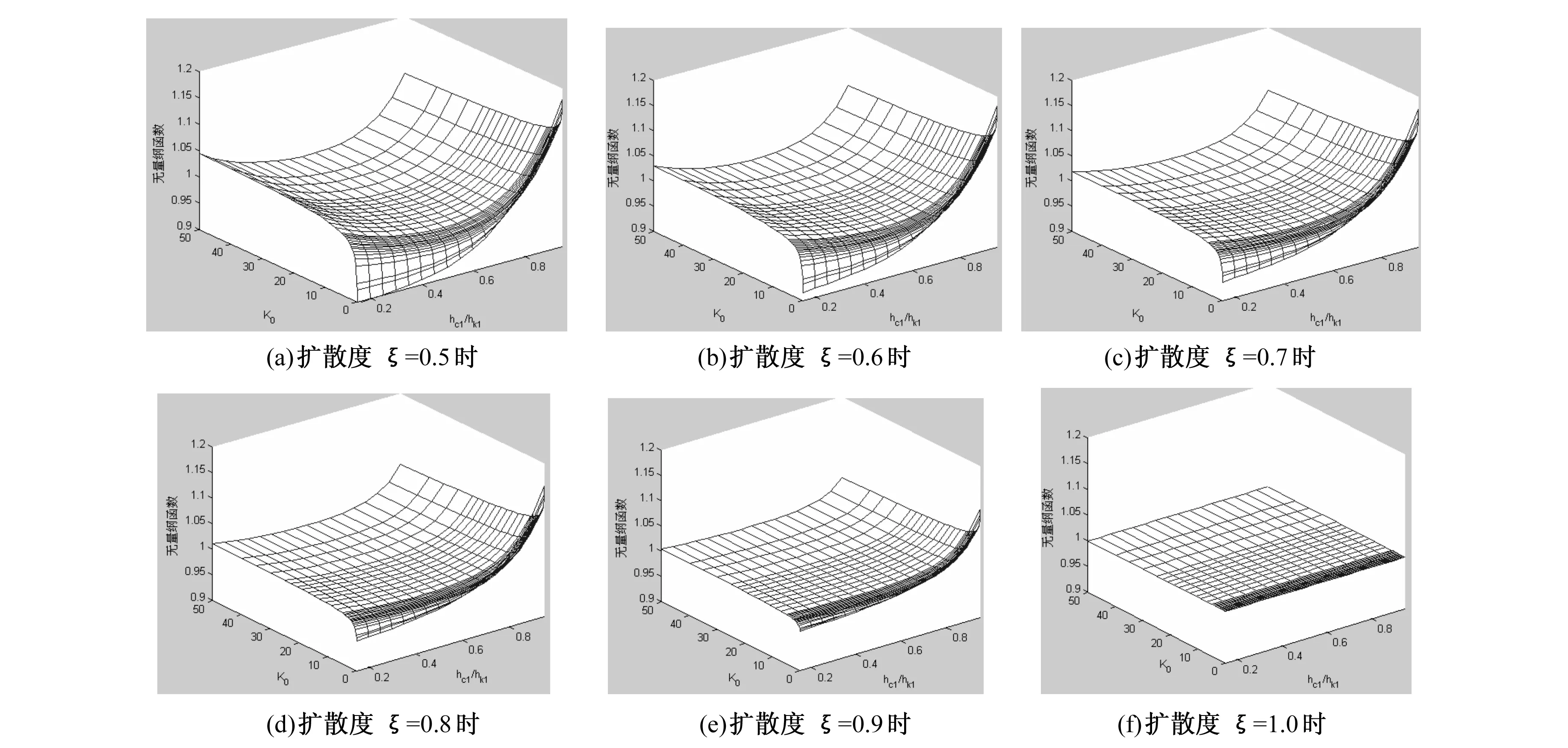
图7 跃后水深初值公式(21)与精确值的比值函数H(x,K0, ξ)曲面关系图
3 结 语
鉴于当前对水闸消力池计算仅适用于矩形断面,而实际工程设计中也有采用梯形翼墙断面情形,根据水力学理论及数学推导,结合Matlab软件及CurveExpert拟合软件,对含扩散型梯形翼墙断面水跃计算进行了深入研究,主要结论如下:
(1)通过数学函数理论及无量纲原理对扩散型梯形翼墙断面水闸消能计算进行分析研究,推出了相对收缩水深直接计算公式,该公式最大相对误差<0.15%,精度完全满足工程计算要求。
(2)根据水力学理论及动量原理,推导了扩散型梯形翼墙消力池水跃共轭水深计算基本方程,并通过数学函数理论给出了无扩散(ξ=1)、扩散型(0.5<ξ<1)梯形翼墙断面跃后水深的直接计算公式,并通过算例分析,认为本文计算公式精度可靠,方便快捷。
(3)通过Matlab软件编程进行数值分析研究,认为本文扩散型(0.5<ξ<1)梯形翼墙断面跃后水深初值计算公式(21)一般情况精度<5%,甚至更高,通过公式(20)迭代一次后最大相对误差一般<1.0%,并给出了跃后水深初值计算公式(21)相对精度随扩散度ξ的影响关系曲面图。
□
[1] 舟山市六横小郭巨围垦工程初步设计[R]. 杭州:浙江省水利水电勘测设计院,2010.
[2] SL-265-2001,水闸设计规范[S].
[3] 黄朝煊, 王贺瑶, 王正中,等. 消力池最不利条件下池深极值探讨[J]. 水力发电学报, 2015,34(1): 79-84.
[4] 王贺瑶, 黄朝煊. 考虑离心力非线性影响的高坝底挑消能收缩水深解析算式研究[J]. 安徽农业科学, 2015,23:187-190.
[5] 李 蕊,王正中,张宽地,等. 梯形明渠共轭水深计算方法[J]. 长江科学院院报, 2012,29(11): 33-36.
[6] 刘 玲, 刘伊生. 梯形渠道水跃共轭水深计算方法[J]. 北方交通大学学报, 1999,23(3):44-47.
[7] 张志昌, 赵 莹. 梯形断面明渠水跃共轭水深新的迭代方法[J]. 西安理工大学学报, 2014,30(1):67-72.
[8] 刘计良,王正中,杨晓松,等. 梯形渠道水跃共轭水深理论计算方法初探[J]. 水力发电学报, 2010,(5):46-49.
[9] R Bakhtyar, D A Barry. Optimization of cascade stilling basins using GA and PSO approaches [J]. Journal of Hydroinformatics, 2009,(11):119-132.
[10] Bakhtyar R, Mousavi S J, Afshar A. Dynamic-programming approach to optimal design of cascade stilling basins [J]. Hydraul. Eng. SCE,2007,133: 949-954.
[11] 王正中,袁 驷. 再论梯形明渠临界水深计算法[J]. 水利学报,1999,(4):14-17.
[12] 黄朝煊. 梯形明渠水力学特征水深的解析计算式研究[J]. 灌溉排水学报, 2015,29(10):46-49.
[13] 黄朝煊. 梯形渠道恒定渐变流水面线计算的新解析法[J]. 长江科学院学报, 2012,29(11):46-49.
