基于DPM模型的离心泵非定常固液两相流及磨损计算

黄 思，邹文朗，周锦驹，何东萍，彭天阳(.华南理工大学机械与汽车工程学院，广州 5064；.中交广州航道局有限公司，广州 500)

离心泵广泛用于航道疏浚、湖泊清淤、河床取土施工中的泥沙水力输送，因此开展离心泵内固液两相流及固体颗粒对泵材料磨损的研究，具有重要的学术和应用价值[1-4]。

目前研究固-液两相流的模型大体可分为两类：一类是欧拉的“双流体模型”，该模型将离散的颗粒相假设为连续的“拟流体”，但当固体颗粒形状、尺寸、碰撞等效应无法忽略时，该模型则与实际情况偏差较大。第二类是拉格朗日的“连续-离散相模型”，计算中将液相视为连续介质，求解欧拉坐标系下的流体控制方程；把固体颗粒相视为离散介质，在拉格朗日坐标系下求解颗粒运动方程，采用迭代计算进行固液两相的耦合。该模型不仅考虑颗粒和流体之间的相互作用，还可考虑颗粒-颗粒、颗粒-壁面之间的碰撞及磨损情况，但该模型在颗粒浓度较高的情况下将使计算时间和成本大为增加。因此该模型一般限于稀疏、小颗粒情形(来流颗粒体积率α<10%)。

因此，本文运用拉格朗日离散相模型(Discrete Phase Model, DPM)[5]，模拟计算离心泵内非定常固液两相流动。磨损计算使用Tulsa大学提出的磨损模型[6]，该模型考虑了颗粒碰撞速度、碰撞角度、材料的布氏硬度以及颗粒的形状等多方面的因素，是目前使用较为广泛的磨损模型之一。

1 计算模型和方法

1.1 计算域及网格划分

选取常用的IS型离心泵作为研究对象，设计参数为：流量Ql=194 m3/h，扬程H=66 m，转速n=2 900 r/min。流动计算域由入口管路、叶轮、蜗壳和出口管路组成。应用ICEM软件进行结构化计算网格划分，并计算水泵的扬程H和效率η等性能参数与网格数目的关系(如图1)。由此可见当网格单元总数为106时，水泵的计算精度较高且占用计算资源较少，此时的六面体结构网格单元如图2所示。本文采用非定常的固液两相流动和磨损计算，旨在更真实地反映旋转叶轮对泵内固体颗粒轨迹所产生的影响[7-9]。设置入口段、泵体与叶轮的交界面为动态的滑移界面，叶轮计算域设在旋转坐标系，其余计算域设在静止坐标系。选取清水作为连续相，石英沙粒(ρ=2 300 kg/m3)作为离散相，粒径范围在0.05～0.2 mm，泵进口颗粒体积率范围在0.5%～3%。

图1 网格单元数与水泵性能参数计算结果的关系

图2 计算域网格单元

1.2 非定常计算方法

在非定常计算中，初始状态(t=0)下泵内流体为静止，计算开始后固相颗粒分别按上述的体积率和粒径从泵入口恒定释放。流体进口边界条件按设计流量值给定，出口边界条件按压力值给定。选取工程中常用的标准k-ε湍流模型，设置流体计算时间步长Δt=60/65nZ，相当于叶轮旋转1°所需的时间。通过监测计算泵扬程H的谐波稳定程度判断非定常计算是否结束。

2 计算结果及分析

2.1 液相流场

通过计算比较发现，不同来流颗粒体积率和粒径所对应的液相流场差别不明显，表明计算所选取的稀疏、小颗粒的固相颗粒对液相流场的影响不显著。作为示例，图3给出流动稳定后液相流速和压力场分布情况(t=2 s，α=3%，dp=0.20 mm)。当两相流动趋于稳定后，由软件后处理得到的水泵计算域内的液相平均速度约为11.4 m/s。

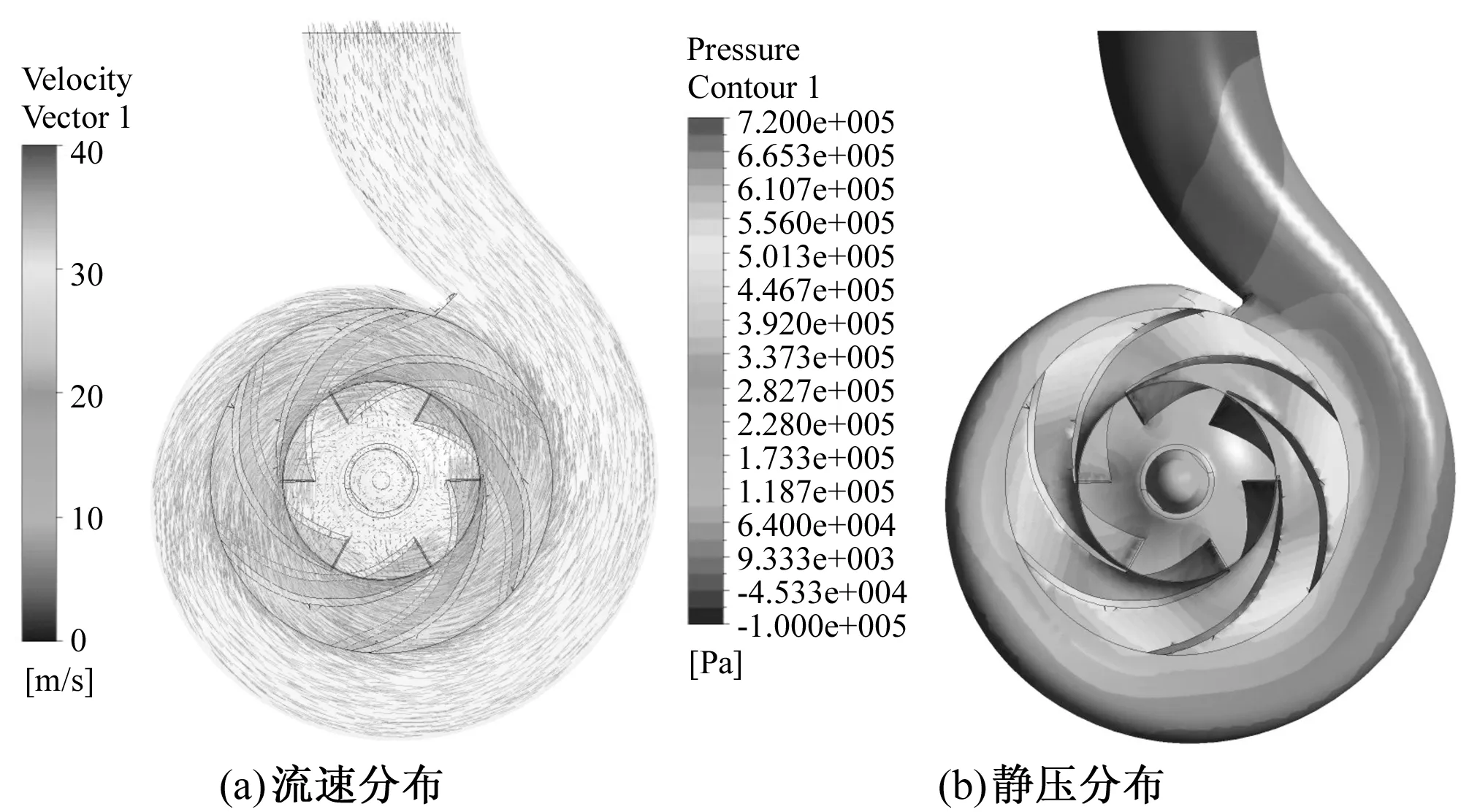
图3 泵内液相流场计算结果(t=2 s，α=3%，dp=0.20 mm)

2.2 固相颗粒流场

图4为流动稳定后泵内固相颗粒速度和位置分布情况(t=2 s，α=3%)。由软件后处理得到的水泵计算域内的固相平均速度约为10.2～11.1 m/s，即两相之间存在一定的整体滑移速度。在颗粒较小的情况下，颗粒跟随流体的性能(简称跟随性)较好，固液相之间的速度差较小，颗粒相对均匀的分布在叶轮和蜗壳内；反之，在颗粒较大的情况下，颗粒跟随性变弱，固液相之间的速度差增加，颗粒在叶轮内集中在叶片工作面一侧，离开叶轮后则聚集在蜗壳外侧壁面。

图4 固相颗粒轨迹(t=2 s，α=3%)

2.3 固相颗粒对泵的磨损率

图5为流动稳定后泵内磨损率的分布情况(t=2 s，α=3%)。由此可见，对于叶轮而言，颗粒的磨损主要在叶片进出口和叶片背面与前盖板相交的位置，颗粒越小，颗粒对叶轮的磨损就越均匀[图5(a)]，泵内的磨损主要体现在叶轮部分。随着颗粒的增大，颗粒逐渐集中在叶片工作面一侧而偏离叶片背面。泵内的磨损由以叶轮部分为主逐渐转变为以蜗壳部分为主，随着颗粒的增大，蜗壳的磨损从隔舌开始逐渐向下游拓展。图5的水泵计算磨损规律与文献[9]采用三坐标精密测量得到的磨损规律基本吻合，表明本文所采用的数值计算方法是切实可行的。

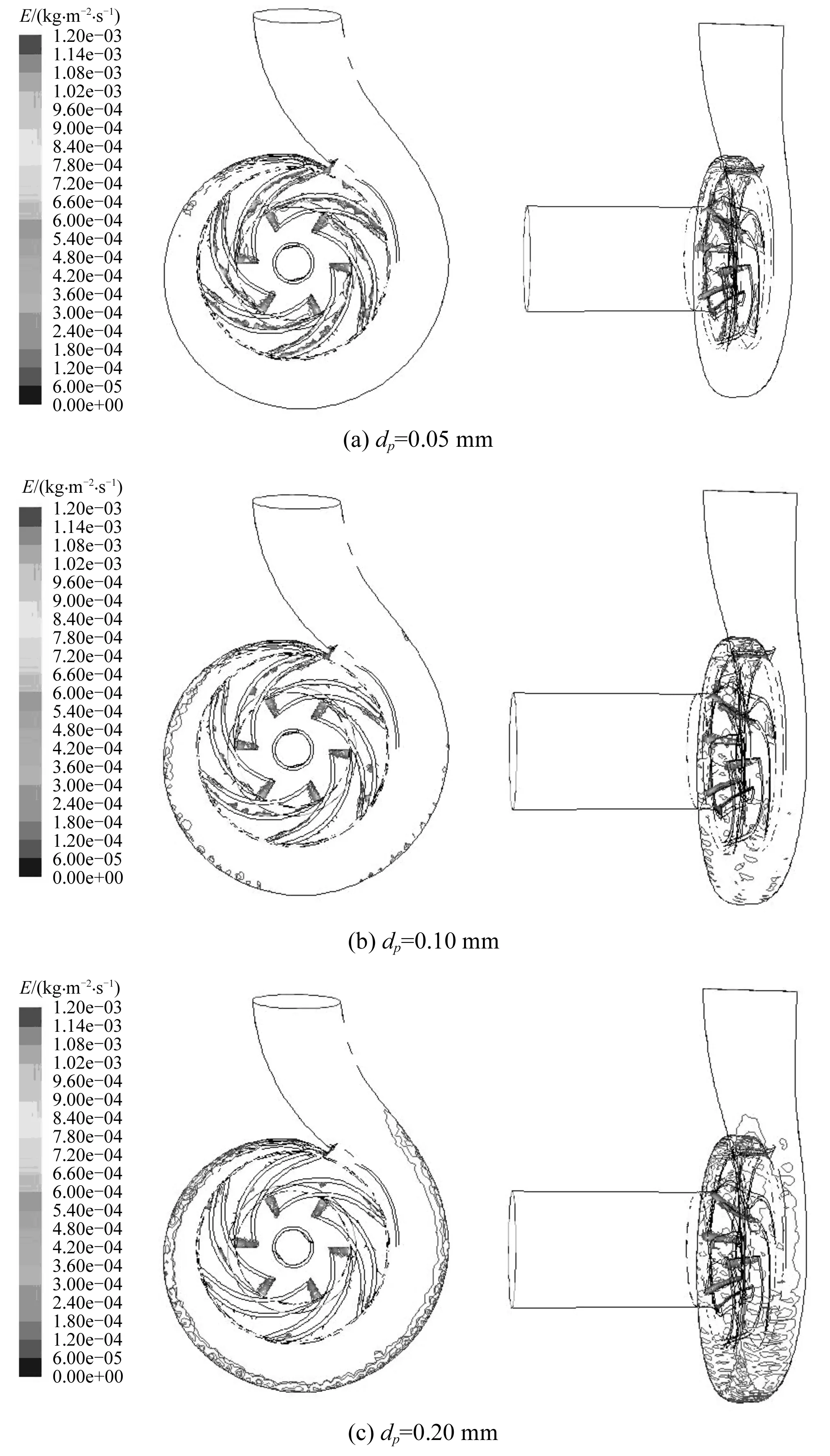
图5 离心泵内磨损率的分布情况(t=2 s，α=3%)

图6和图7分别给出后处理得到的泵内面积平均磨损率(Erosion in Area-Weighted Average)随泵进口颗粒体积率和颗粒粒径的变化曲线(t=2 s)。由图6可见，无论是进水管、叶轮还是蜗壳，平均磨损率随泵进口颗粒体积率的增大而增加。对叶轮部分[图7(a)]，平均磨损率随着颗粒粒径的增大而相对减少；而在蜗壳部分[图7(b)]，平均磨损率随着粒径的增大而相对增加。但总体上，离心泵的平均磨损率随着颗粒粒径的增大而增加[图7(c)]。

图6 平均磨损率随泵入口颗粒体积率的变化曲线(t=2 s)

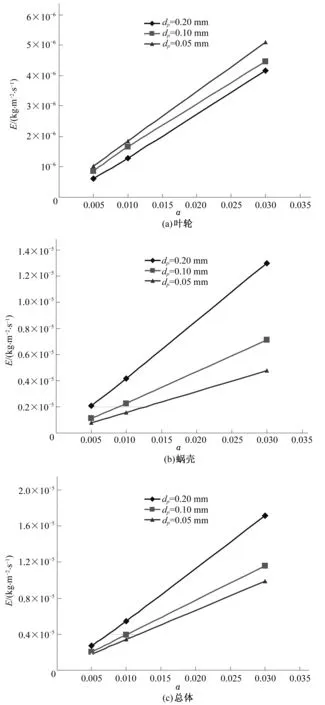
图7 平均磨损率随颗粒粒径的变化曲线(t=2 s)

3 结 论

(1)在颗粒较小的情况下跟随性较好，颗粒相对均匀地分布在叶轮和蜗壳内；在颗粒较大的情况下，颗粒跟随性变弱，固液相之间的速度差增加，颗粒在叶轮内集中在叶片工作面一侧，离开叶轮后则聚集在蜗壳外侧壁面。

(2)颗粒的磨损主要在叶轮叶片进出口和叶片背面与前盖板相交的位置，颗粒越小对叶轮的磨损越均匀，蜗壳的磨损则不明显。随着颗粒的增大，泵内的磨损逐渐以蜗壳的磨损为主，蜗壳的磨损从隔舌开始逐渐向下游拓展。

(3)泵内的平均磨损率随泵进口颗粒浓度的增大而增加。随着颗粒粒径的增大，叶轮的磨损率相对减少，蜗壳的磨损率相对增加，但总体上离心泵的平均磨损率增加。

□

[1] Wilson K C, Addie G R, Sellgren A, et al. Slurry transport using centrifugal pumps[M]. Springer Science & Business Media, 2006.

[2] 胡庆宏，胡寿根，孙业志，等. 固液两相流泵的研究热点和进展[J]. 机械研究与应用， 2010,(5)：1-4.

[3] 黄 思，杨富翔，宿向辉. 运用CFD-DEM耦合模拟计算离心泵内非稳态固液两相流动[J]. 科技导报, 2014,32(27):28-31.

[4] 朱祖超，崔宝玲，李 昳，等. 双流道泵输送固液介质的水力性能及磨损试验研究[J]. 机械工程学报, 2009,45(12):65-69.

[5] Fluent Ansys. Theory guide[M]. US: ANSYS Inc, 2009.

[6] Mclaury B S. A model to predict solid particle erosion in oilfield geometries[D]. University of Tulsa, 1993.

[7] 董富弟. 单级双吸式离心泵在输送含沙水流下的流动与磨损特性研究[D]. 兰州：兰州理工大学, 2014.

[8] 董文龙, 李 昳. 离心泵内大颗粒下运动特性数值模拟与磨损分析[J]. 机电工程, 2015, 32(3)：324-327.

[9] 陈 思, 王尊策, 吕凤霞,等. 基于离散相模型的电潜泵叶轮磨损数值计算[J]. 中国石油大学学报：自然科学版, 2015,39(3)：143-148.