考虑参数不确定的区域水资源配置鲁棒优化模型研究
2016-03-22吴鑫淼郄志红河北农业大学城乡建设学院河北保定071001
王 彪,吴鑫淼,郄志红(河北农业大学城乡建设学院,河北 保定 071001)
区域水资源的优化配置是在可利用总水量有限的前提下,综合考虑社会、经济、环境的协调发展,发挥总水量最大的效益,实现最优化调度,而得到水量最优分配方案,达到人水和谐,实现水资源的可持续利用和经济社会的可持续发展,是典型的非线性多目标优化问题[1-3]。
传统水资源优化配置,对目标函数求解时,往往所考虑的优化配置参数是确定的,但这些参数在实际情况下不是一成不变的,如:单方水产量、粮食价格、万元产值需水量等,假定这些参数变化规律服从一定的随机分布,故参数的变化必然导致优化结果的不稳定;另外,传统遗传算法在全局离散优化方面的优越性广为所知,但进化过程中容易逐渐丧失种群多样性,产生早熟现象[4,5],从而影响优化效率和精度。近几年人们提出的病毒进化遗传算法加设病毒种群可有效改善种群多样性,提高遗传算法的全局搜索能力,从而避免这种现象[6]。故此,本文应用病毒进化遗传算法求解区域水资源优化配置问题,而在求解的鲁棒性方面,则通过在优化目标中添加方案的鲁棒性评价优化性能的办法。
1 区域水资源优化配置模型
水资源配置一般为多目标优化问题,这里通过加权的方法,即:基于区域水资源应用现状及可持续发展的要求,把区域供水产值之和与粮食产量这两个目标,分别乘以w1、w2的权重后相加,作为综合优化目标,以区域重要污染物(COD)排放量、水源供水总量及各用户需水量要求作为约束条件,建立了如下水资源优化配置模型,具体为:
(1)经济子目标。
(1)
为清除量纲影响,将目标进行归一化:
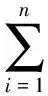
(2)
则归一化后目标为:
(3)
式中:n为水源个数;m为工业、农业及居民生活等用水户个数;Xij为水源i供给j用户的水量,万m3;bij为水源i向j用户的单位供水量的效益系数,元/m3;cij为水源i对j用户的单位供水量的成本系数,元/m3;maxbi为i用户的最大单方用水效益,元/m3;minci为i用户的最小单方用水成本,元/m3;maxXi为i用户的最大用水量,万m3。
(2)社会子目标。
(4)
为清除量纲影响,将目标进行归一化:
maxf22(X)=maxX·maxF
(5)
则归一化后目标为:
(6)
式中:Xi1为各水源供农业的用水量,万m3;F为每万方水粮食产量,万t/万m3;maxX为水源供给用户的最大水量,万m3;maxF为每万方水最大粮食产量,万t/万m3。
(3)综合目标。
f(X)=w1f1(X)+w2f2(X)
(7)
式中:f1(X)为转化之后的经济目标;f2(X)为转化之后的社会目标。
约束条件:
(1)重要污染物COD的排放量约束[7]:
(8)
式中:dj为j用户的单位废水排放量中重要污染物COD的含量,mg/L;pj为j用户废水排放率;[COD]为COD排放的允许最大值,t。
(2)水源可供水量约束:由于本地区缺水,考虑了水量完全分配,所以本公式定义为等式约束:
(9)
式中:Wi表示水源i的可供水量,万m3。
(3)用户需水量约束:
(10)
式中:Lj、Hj分别为用户j的最小、最大需水量,万m3。
(4)非负约束:
Xij≥0
(11)
2 病毒进化遗传算法的具体实现
2.1 病毒进化遗传算法
病毒进化遗传算法是1996年日本教授 Kubota从生物病毒进化系统中改进而来的一种遗传算法,是一种协同进化算法。与传统遗传算法相比最主要特点是有两个群体:主群体和病毒群体,既能进行全局搜索,在父子代群体间纵向传递继承信息;又能进行局部搜索,在同一群体中横向传播进化。因此,病毒进化遗传算法具有更快的收敛速度,更好的优化效果[8]。
病毒进化基本步骤如下:
(1)确定病毒的编码方式和参数集合。编码方式一般与主群体相同,参数集合包括病毒种群个体数VINU、病毒染色体长度LONG、病毒染色体最大长度MAXLONG、病毒感染率infrate、病毒感染率调整系数A、病毒适应值fitvirus、病毒生命力life、生命力折减系数decay等。
(2)从主群体中随机抽取个体q,从个体q中随机抽取长度为LONG的基因作为病毒基因,重复操作VINU次,构成初始病毒数据库VE[VINU]、virus[LONG]。
(3)以感染率infrate对宿主群进行感染操作,并记录每个病毒个体的宿主VE[i].hostnum,以及病毒感染前后宿主的适应度VE[i].fithost[0]、VE[i].fithost[1]。
(4)计算病毒个体适应度、感染率及生命力。
VE[i].fitvirus=VE[i].fithost[1]-VE[i].fithost[0]
如果VE[i].fitvirus>0 ,表示宿主个体被感染后适应度有所提高,则病毒i个体的感染率有所提高,即:
VE[i].infrate=(1+A)×VE[i].infrate
如果VE[i].fitvirus < 0 ,表示宿主个体被感染后适应度有所降低,则病毒i个体的感染率有所降低,即:
VE[i].infrate=(1-A)×VE[i].infrate
病毒感染后生命力等于原病毒生命力折减以后与病毒适应度之和,即:
VE[i].life=decay×VE[i].life+VE[i].fitvirus
(5)当VE[i].fitvirus>0说明病毒基因为优良基因,增加病毒基因长度;当VE[i].fitvirus<0 说明病毒基因为不良基因,减小病毒基因长度。VE[i].life<0 病毒生命力为0,重新生成病毒基因,更新病毒基因库。
(6)本次病毒感染操作完成,判断是否达到进化代数,未达到则进入步骤(3);达到则进入步骤(7)。
(7)完成。
2.2 染色体编码
染色体编码方式在一定程度上决定算法效率的高低和程序设计的复杂程度[9]。由于本模型涉及到多水源供水的情况,如果采用传统的随机分配各用户的水量对染色体编码,会出现遗传个体不满足水源供水总量要求的问题。因此,本文提出了采用配水系数对染色体编码,并通过配水系数的归一化处理使遗传操作的每一代个体均满足优化模型中约束条件(2)的要求,避免了不满足条件个体的重新生成,提高了优化效率。图1为染色体DNA结构,采用十进制方式编码。通过对张家口市来水及需水情况调查,确定3个供水水源分别为地表水、地下水和其他水源;用水户分别为农业、工业、农村居民生活和城镇居民生活用水。

x11x12x13x14x21x22x23x24x31x32x33x34
图1染色体DNA结构
配水系数都是0~7的随机数xij,直接用其换算分配水量值,同样会出现用户分得的水量总和与水源供水量不等的情况,因而对配水系数做归一化处理,再用归一化后的配水系数乘以相应水源的供水量得到分配的水量值Xij,作为评价函数的决策变量。
同一水源配水系数的归一化并换算成分配给j用户的水量计算公式为:
(12)
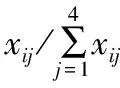
2.3 选择满足约束条件染色体的方法
对初始生成的染色体不满足本地区重要污染物COD的排放量约束、用户需水量约束的,重新生成染色体。对种群中满足约束条件的染色体,如重要污染物COD的排放量在规定范围内的,提升染色体适应度、当分配的用水量满足用户需求的,再次提升染色体适应度;不满足约束条件的适应度不提升。通过提升适应度的方法对染色体进行奖励,来选择优秀的染色体用于遗传。
2.4 算法改进——引入染色体年龄结构评价
本文引入年龄的概念来对每个染色体进行评价,该年龄是指染色体被延续的代数。个体年龄越高,则代表其在用水成本、效益以及单方用水产生的污染物质等参数不确定性的条件下能保存下来,说明其适应性越强,具有较好的鲁棒性。子代年龄增加概率定义为:
P=f(D,σ)
式中:D为子代与父代的距离,用不同基因的个数表示;σ为子代与父代距离的标准差,指子代与父代距离与本代平均水平的差距。
加入年龄结构后,适应度函数如下:
式中:g(yj)为子代个体j的适应度;dj为子代个体j的年龄;g(pj)为子代个体j的父代个体的适应度。
2.5 病毒进化遗传算法程序
实现过程描述如图2。

图2 病毒进化遗传算法程序
3 实例分析
利用病毒进化遗传算法及上述模型对河北省张家口市中长期规划年2020年和2030年的水资源进行优化配置。表1为张家口市水资源预测结果。该市属于干旱半干旱地区,水资源短缺,为满足用户的需水要求及经济社会发展需求,对区域的各个水源进行了完全分配。

表1 不同规划年水源可供水量 万m3Tab.1 Water supply of different planning years
本文水资源优化配置的目的就是合理的分配有限的水资源,达到综合效益最优。
遗传参数的选择:取种群大小NUM=300;染色体编码长度GENE=12;最大进化代数maxgen=200。区域的水资源优化配置结果(见表2),其中包括在考虑参数不确定和不考虑参数不确定两种情况。为进一步比较两种情况下对区域水资源的优化效果,将成本系数、效益系数和粮食产量系数进行1 000次蒙特卡罗模拟,根据结果画出概率分布图(见图3),并分别计算概率分布的均值及方差(见表3)。
由图3可看出,2020年中考虑参数不确定的综合目标值的概率分布曲线[图3(a)]比不考虑参数不确定的综合目标值的概率分布曲线[图3(b)]中间部分集中、两边分布均匀且均值在0.8~1之间;2030年中考虑参数不确定的综合目标值的概率分布曲线[图3(c)]比不考虑参数不确定的综合目标值的概率分布曲线[图3(d)]两边分布均匀、中间区间值的个数多且曲线的均值大。由表3的数据可以验证以上得出的结论,图3(b)方差0.007 5大于图3(a)图0.007 2,说明图3(b)较离散,综合目标值波动大;图3(a)均值0.856 0大于图3(b)0.720 2,说明a图的综合目标值较大。对比2030年的图3(c)和图3(d),也会得出相似结论。
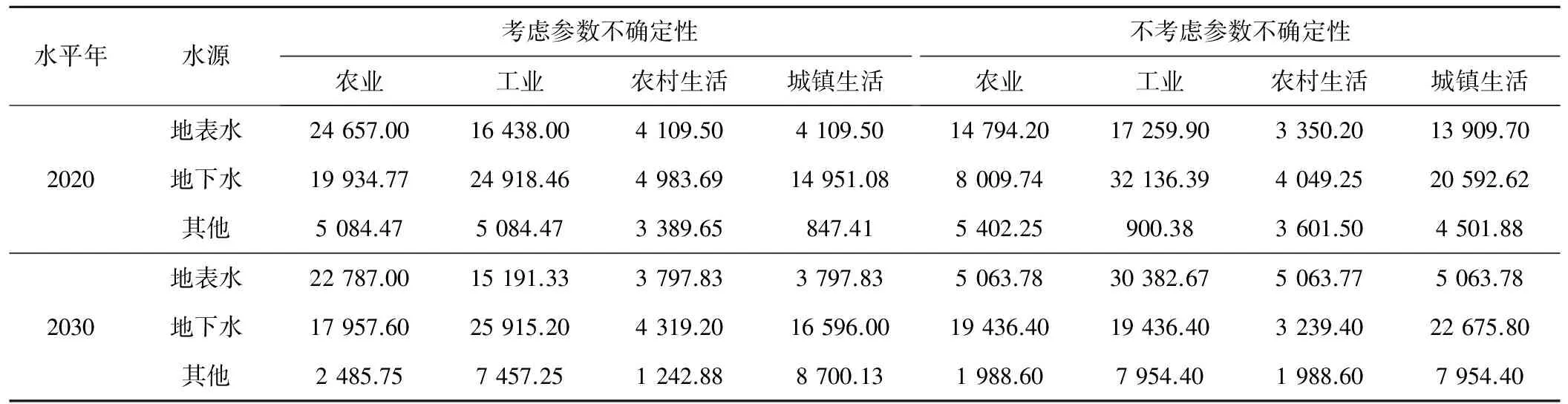
表2 两种情况下水资源优化配置结果 万m3Tab.2 Two kinds of water resources optimal allocation results

图3 两种情况下目标值的正态分布图
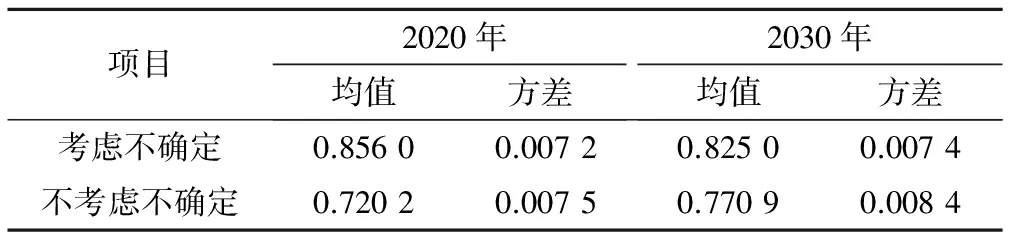
表3 两种情况下目标值的均值和方差的比较Tab.3 Comparison of mean and variance of target values in two cases
4 结 论
(1)本文运用病毒进化遗传算法来对水资源优化配置中考虑参数不确定的优化模型进行求解,并通过实例分析验证了该算法具有可行性和鲁棒性,表明该方法实现了对水资源的优化配置。
(2)体现了运用该思想和算法得出的优化配置结果具有实用性和正确性,结果可以为区域水资源可持续利用和规划管理的决策提供参考依据。
(3)虽然本文旨在考虑参数波动符合正态分布的情况下对区域水资源进行优化配置,参数选取也会有所局限,但为进一步解决多水源、多用户、多约束的水资源优化配置问题提供了新思路、新方法。
□
[1] 杨斌斌,孙万光. 基于并行粒子群算法的跨流域调水优化模型研究[J]. 中国农村水利水电,2015,(3):10-13.
[2] 左其亭. 人水和谐论-从理念到理论体系[J]. 水利水电技术,2009,8(40):25-28.
[3] 吴泽宇,索丽生. 水资源优化配置研究进展[J]. 灌溉排水学报,2004,2(23):1-3.
[4] 张晓缋,戴冠中,徐乃平. 遗传算法种群多样性的分析研究[J]. 控制理论与应用,1998,(1):17-23.
[5] 何燕平,何 辉,张筱磊. 遗传算法中群体多样性评价指标的研究[J]. 哈尔滨工业大学学报,2009,(3):67-70.
[6] 王 鑫,郄志红,吴鑫淼,等. 基于改进病毒进化遗传算法的渡槽维修计划优化[J]. 水利水电技术,2014,(9):39-41.
[7] 陶 洁,左其亭,薛会露,等. 最严格水资源管理制度“三条红线”控制指标及确定方法[J]. 节水灌溉,2012,(4):64-66.
[8] 刘晶晶,黄 明,梁 旭. 改进的病毒进化遗传算法应用研究[J].大连交通大学学报,2009,2(30):82-85.
[9] 李 琳,吴鑫淼,郄志红. 基于改进NSGA-II算法的水资源优化配置研究[J]. 水电能源科学,2015,4(33):34-36.
