InfoWorks水文模型参数灵敏度分析及其随区域尺度的变化

常 青，李江云，周 毅(武汉大学土木建筑工程学院, 武汉 430072)

0 引 言

近年来，EPASWMM，InforWorksICM等雨洪模型在我国得到了较广泛的使用。在雨洪模型的众多参数中，一些参数的变化对模拟结果影响较大，而另一些参数却微乎其微。对敏感性较强参数的准确取值，可提高模拟结果的可靠性。因此，需要根据模型参数变化引起的响应进行分类，即参数敏感性分析，然后对较敏感的参数进行率定，避免了调参过程的盲目性，从而提高参数率定的效率和模型模拟的可靠性。参数灵敏度分析是模型校核的基础，参数灵敏度分析能使人更了解模型的表现规律。灵敏度也是参数识别、检验模型最基本的手段之一[1]。

国内外诸多学者对于各种雨洪模型进行了参数灵敏度的分析研究。谭琼等[2]采用局部灵敏度分析方法来检验单个参数对径流量和洪峰流量的影响，得出径流系数影响因素最大，坡度影响因素最小。黄金良等[3]选取了3场实测降雨，对澳门半岛雅廉坊小流域的SWMM模型相关参数运用Morris筛选法进行局部灵敏度分析，发现不同降雨强度下，模型水文水力模块的灵敏参数有所差异，尤其是与下渗率相关的参数,雨强最大的降雨,最大和最小下渗率为中等灵敏参数,而雨强较小的降雨则为不灵敏参数。张胜杰[4]等对于北京某住宅小区在两场特征不同的实测降雨下的研究表明，对于径流总量和径流峰值，不透水率，子汇水区面积，汇水区宽度为敏感参数，降雨强度较大时下渗参数为中等敏感参数，降雨强度较小时为不敏感参数。先前对于参数灵敏度的研究大都偏重灵敏度本身，较少考虑雨型的及模型尺度的不同对灵敏度的影响，而根据Mun-Ju S[1]等人的研究，参数灵敏度会随着模型尺度、研究区域的大小的不同而变化。本文将以某平原地区一独立排水流域为例，在考虑到降雨因素的同时，探讨灵敏度在排水区不同模型尺度下的变化规律。

1 模型简介及灵敏度分析方法

1.1 ICM计算模型简介

InfoWorks ICM模型系统能够模拟雨水管道系统，广泛应用于排水系统现状评估，城市洪涝灾害预测评估，城市降雨径流控制及调蓄池设计评估[5-7]，模型由降雨径流模块、管流模块、污水模块、河道模块以及水质模块等构成。根据不同的下垫面，软件采用不同的计算方法，主要的计算单元有产流模型，汇流模型以及管流模型。对于产流模型以及汇流模型，InfoWorksICM整合了多种不同的模型来模拟这两个过程，常用的产流模型有固定比例径流模型，Wallingford固定径流模型，新英国可变径流模型，Horton模型，SCS下渗模型，Green-Ampt下渗模型，固定下渗模型等。常用的汇流模型有双线性水库模型，大型汇水面积径流模型，SPRINT径流模型，Debordes径流模型，SWMM模型。固定径流系数模型原理较为简单，参数数量较少，而SWMM汇流模型使用较为广泛，参数取值依据性较强，所以本次计算产流模型选用固定径流系数模型，汇流模型选用SWMM径流模型。

1.2 灵敏度分析方法

常用的模型灵敏度分析方法有Morris法[8]以及Sobol法[9]。Morris灵敏度方法是Morris在1991年提出的一种全局灵敏度方法，该方法简单，易于操作，计算量小，可以分析多个参数在较大范围内同时发生变化时对模型输出的影响。Sobol灵敏度分析方法是一种基于方差的蒙特卡罗法，Sobol方法可应用在非单调、非线性、非叠加等模型，但相比Morris法，计算量相对较大，操作较为复杂。本文选用Morris法来计算模型的灵敏度。

Morris筛选法选取模型参数中某一变量 ，其余参数值固定不变，在所选参数阈值范围内随机改变xi，运行模型得到目标函数y(x)=y(x1,x2,x3,…,xn)的值，用影响值ei判断参数变化对输出值的影响程度，用下式计算，

ei=(y*-y)/Δi

(1)

式中：y*为参数变化后的输出值；y为参数变化前的输出值；Δi为参数i的变幅。

本文采用修正的Morris法[10]进行参数敏感性分析，将所选变量以固定步长百分率变化，然后计算Morris系数的多个平均值，求得敏感性判别因子S，如下式：

(2)

式中：S为敏感性判别因子；n为模型运行次数；i为模型的第i个状态变量；Yi为模型第i次运行输出值；Y0为参数调整后计算结果初试值；Pi为第i次模型运行参数值相对于校准后参数值的变化百分率；Pi+1为第i+1次模型运算参数值相对于校准后初始参数值的变化百分率。

计算时，对于目标参数，以5%为固定步长对某一参数值进行扰动，分别是目标参数初始值的80%，85%，90%，95%，105%，110%，115% 和120% ，而其他参数值固定不变，观测不同降雨强度的径流量和峰值流量的水文和水力模块相关参数的灵敏度。根据灵敏度定量表达的结果，可将灵敏度分为4 类[10]。 为高灵敏参数；0.2≤|S|<1为灵敏参数；0.05≤|S|<0.2为中等灵敏参数；0≤|S|<0.05为不灵敏参数。

2 分析实例及结果

2.1 研究区域介绍

本研究区域为湖南某市城北排水片区，位于市区西北部。研究区域地处湖南省西南部，属亚热带季风气候，多年平均降水量1 423.9 mm，降水集多中在3-8月。研究区域属于典型的城市地形，地势平缓，总体坡度较小，区域内大部分属于老旧城区，少部分属于新建成区域。总面积为374.4 hm2，不透水面积约占62.5%。根据研究区域内下垫面汇水情况以及排水管线情况将研究区域分为126个子汇水面积。根据实际情况以及模型手册，将各个参数输入到模型中，建立该区域的暴雨径流模型。选取特征宽度、坡度、初期损失值、管长、地表曼宁N值、径流系数以及管道曼宁N值这7个参数为研究对象。各主要参数的初始取值见表1。

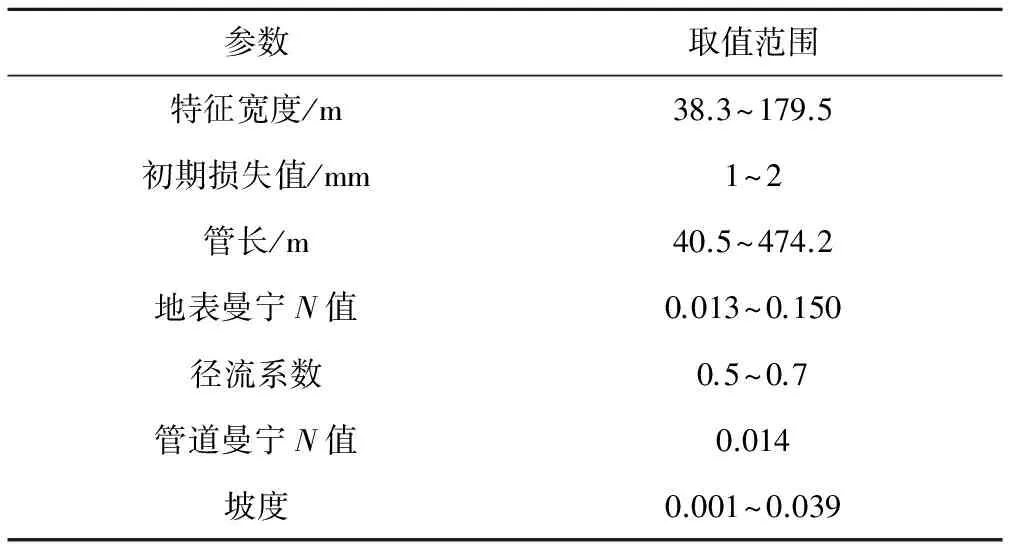
表1 参数的初始取值Tab.1 Calibration parameters and their initial values

在不同的尺度下，模型的参数灵敏度可能会有所不同，甚至参数的灵敏度在每个子流域上都各不相同[1]。如图1，为了考虑区域尺度影响，将研究区域分为A,B,C三个不同大小的区域，A为整个区域；B为区域北部的24个子汇水面积构成的流域，面积为87.78 hm2；C为流域末端的1个子汇水面积构成的流域，面积1.78 hm2。经过模型验证后，对于3个区域，分别计算各个参数的灵敏度。

图1 研究区域及其划分Fig.1 Study area and its scale variations

降水数据由研究区内的雨量站获得．由于部分暴雨洪水资料的缺失，选取2012年资料较完整的2场降雨进行模拟，为了更好地探究雨型与参数灵敏度的关系，在此选用2场较有代表性的降雨，其中2012-05-06降雨为较长历时，降雨强度较小的一场降雨。2012-07-12降雨为当年降雨强度最大且历时较短一场降雨，降雨特征见图2。

图2 降雨过程线Fig.2 Graph of precipitation characteristics

2.2 结果与分析

根据修正的Morris 筛选法，利用灵敏度公式计算水文水力模块中参数的敏感性S，得到各个参数对研究区径流总量和径流峰值的灵敏度，见表2。模型尺度以及降雨对参数的敏感性分析结果有较大影响。

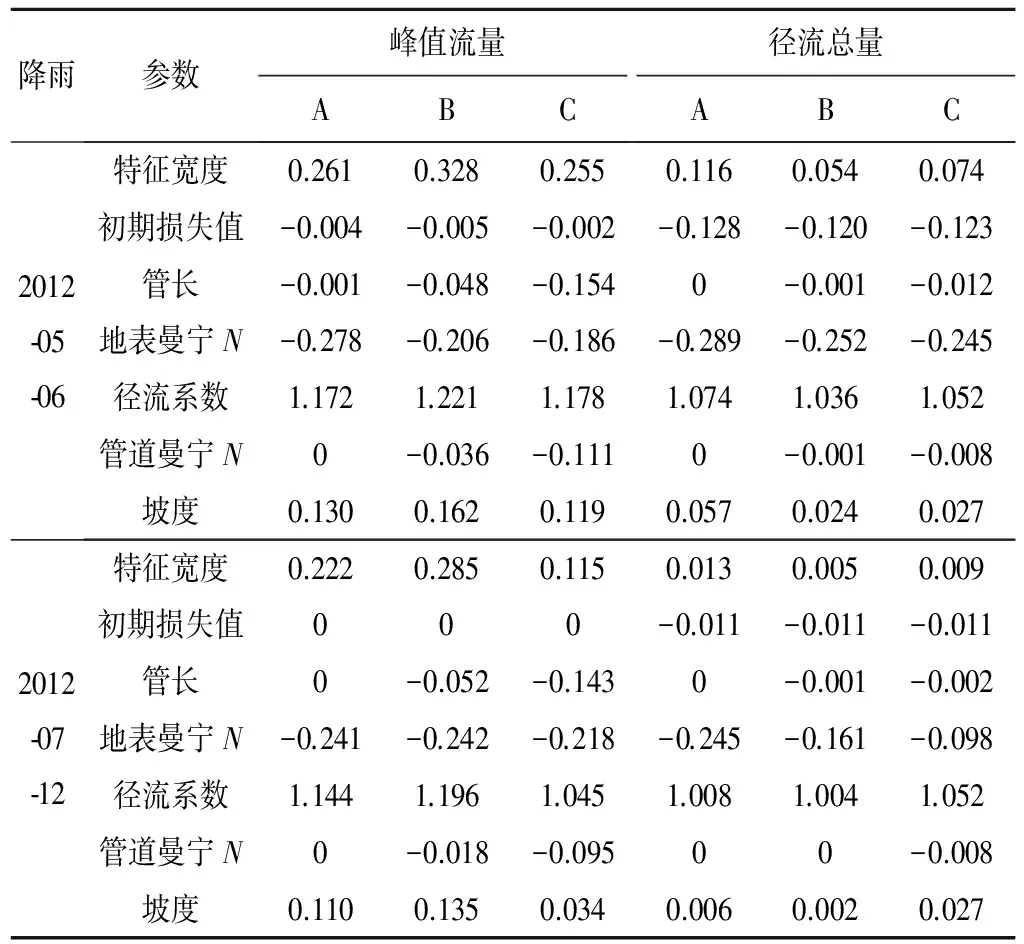
表2 模型参数敏感性Tab.2 Parameter sensitivity values

2.2.1主要参数的灵敏度分析排序

对于InfoWorksICM模型径流峰值影响较大的参数依次为，径流系数，特征宽度，地表曼宁N，以及坡度，其中径流系数为高灵敏参数，特征宽度以及地表曼宁N一般为灵敏参数，坡度为中灵敏参数。初期损失值，管长以及管道曼宁N这3个参数对径流峰值的影响较小。

对径流总量而言，敏感性较大的参数依次为径流系数，地表曼宁N，初期损失值以及特征宽度。其中径流系数为高灵敏参数，地表曼宁N，初期损失值以及特征宽度一般为中灵敏参数。坡度，管长以及管道曼宁N一般为不灵敏参数。

总的来说，径流系数为最敏感的参数，无论在何种降雨何种尺度下，其均为高灵敏参数，且其灵敏度远远高于其他参数。这种情况下，模型的结果高度依赖一种参数，因此对于这个参数的率定应当非常谨慎[1]。

2.2.2参数灵敏度随区域尺度的变化

由表2可知，随着区域尺度的增大，管长对于径流峰值以及径流总量的灵敏度也随之增加。图3(a)给出了管长对径流峰值的灵敏度随区域尺度变化的趋势，可看出管长由不灵敏参数变为中等灵敏参数。同样地，随着区域尺度增大，管道曼宁N对于径流峰值以及总量的灵敏度也随之增大。说明随着区域尺度的增大，管道相关参数的影响会随之增大，所以当研究区域较大时，应增强对管道长度以及管道曼宁N取值的精确性。

地面曼宁N也同区域尺度有较明显的相关性，图3(b)表示了2012-05-06降雨下，地面曼宁N的灵敏度随区域尺度的变化。可以看出，无论是对于径流系数或径流总量，地面曼宁N的灵敏度随区域增大而减小。

同时，由表2可知，其余的参数如特征宽度，初期损失值，径流系数以及坡度这几个参数的灵敏度的变化与区域尺度无明显联系。

2.2.3雨型对参数灵敏度的影响

初期损失值本身的灵敏度较低，一般为不敏感参数，但初期损失值的灵敏度受到雨型的影响较大。初期损失值对径流总量以及径流峰值的灵敏度，在2012-05-06降雨下普遍要高于2012-07-12降雨。图3(c)表示了初期损失值对径流总量的灵敏度在两场降雨下的灵敏度变化。这主要是由于两场降雨的总降雨量相差悬殊，当降雨量很大时，降雨初损对总径流量的影响会相对较小。由表2还可看出，特征宽度、地面曼宁N以及坡度的灵敏度，在2012-05-06降雨下普遍高于2012-07-12降雨，这主要是因为较大的降雨量以及降雨强度削弱了雨水汇流参数的影响。

3 结 语

InfoWorks模型对于峰值流量或径流总量，其参数灵敏度总体上一致。径流系数均为最敏感参数，对于峰值流量或径流总量，其灵敏度值都在1以上，因此模型参数率定时应特别注意径流系数的取值。其次为地面曼宁N，坡度，特征宽度这几个汇流模型中的参数，一般属于灵敏参数。初期损失值一般为中灵敏参数。管道长度以及管道曼宁N值属于不灵敏参数。

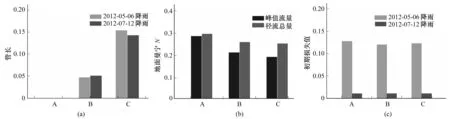
图3 不同区域、降雨下的参数灵敏度比较Fig.3 Sensitivity comparisons under different scale and precipitation

多数参数对于峰值流量的灵敏度高于径流总量的灵敏度。总体而言，产汇流模型的参数更加敏感，而管道流模型参数相对不敏感。

在本例中，特征宽度以及初期损失值的灵敏度受到雨型的影响较大。另外，地面曼宁N对于径流总量的灵敏度在不同降雨下也有较大变化。地面曼宁N值以及管道曼宁N值的灵敏度随着区域的增大而减小，管长的灵敏度随着区域尺度的增大而增大。径流系数、坡度、特征宽度则与同区域大小没有明显相关性。

本研究的结果可为今后湖南及相近地区InfoWorksICM水文模型参数率定提供参考，减少建模工作量，提高参数率定效率。

□

[1] Mun-Ju S, Joseph H A, Guillaume, et.al. Addressing ten questions about conceptual rainfall-runoff models with global sensitivity analyses in R [J]. Journal of Hydrology, 2013,503:135-152.

[2] 谭 琼，李 田，周永潮，等.城市雨水管网模型参数的率定与评价[J]. 湖南大学学报(自然科学版)，2008,35(1):31-35.

[3] 黄金良，杜鹏飞，何万谦，等．城市降雨径流模型的参数局部灵敏度分析[J]．中国环境科学，2007,27(4):549-553.

[4] 张胜杰，宫永伟，李俊奇. 暴雨管理模型SWMM水文参数的敏感性分析案例研究[J]. 北京建筑工程学院学报，2012,28(1):45-48.

[5] Christopher Zoppou. Review of urban storm water models[J]. Environmental Modelling & Software 2001,16:195-231.

[6] A H Elliott, S A Trowsdale. A review of models for low impact urban stormwater drainage [J]. Environmental Modelling & Software, 2007,22:394-405.

[7] 黄国如，冯 杰，刘宁宁，等. 城市雨洪模型及应用[M].北京：中国水利水电出版社, 2013:227-239.

[8] Morris M D. Factorial sampling plans for preliminary computational experiments [J]. Technometrics, 1991,33(2):161-174.

[9] I M Sobol. Global sensitivity indices for nonlinear mathematicalmodels and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001,55:271-280.

[10] 林 杰，黄金良，杜鹏飞，等. 城市降雨径流水文模拟的参数局部灵敏度及其稳定性分析[J]. 环境科学, 2010,31(9):2 023-2 028.