基于熵权和余弦决策模型的物流服务商选择研究

2016-03-22邹浩

赤峰学院学报·自然科学版 2016年4期

关键词：信息熵选择模型

邹浩

（湖南财政经济学院　工商管理系，湖南　长沙　410205）

基于熵权和余弦决策模型的物流服务商选择研究

邹浩

（湖南财政经济学院工商管理系，湖南长沙410205）

摘要：本文针对影响物流服务商选择的各种因素，从服务水平、企业规模、企业信誉以及物流成本四个主要方面建立了物流服务商选择评价指标体系.考虑到各指标之间相互关系的重要性，采用信息熵理论确定各指标权重，并基于余弦决策法，建立了基于熵权和余弦决策法的物流服务商选择模型.最后通过算例分析对模型的科学性和有效性进行了验证.

关键词：信息熵；余弦决策；物流服务商；选择；模型

引言

随着信息技术和全球经济一体化的高速发展，社会分工越来越细，市场竞争也更加激烈.为了满足消费者需求的多样性，企业之间更多的是竞争与合作的关系.此时，企业为了获得核心竞争力，将专注于自身优势方面的发展，而将自身不擅长的业务部分或者全部交由物流服务商进行资源整合，以降低物流成本，提高核心竞争力，最终实现双赢的目的[1].因此，选择一个较好的物流服务商对企业的发展至关重要.

物流服务商作为企业发展的战略伙伴，不仅能够降低物流成本，增强企业客户关系管理，而且能够增强企业竞争力，直接影响企业未来发展.近年来，已有不少学者利用不同的研究方法，从不同角度对其进行了深入研究.文献[2]采用DEA-AHP评价方法，分别从经济性、信息化水平和发展潜力三个因素构建了农产品物流服务商评价指标体系，并结合物流服务商客观数据和农民主观偏好，进行了综合评价；文献[3]结合定性分析与定量分析，探讨了物流网络覆盖、运费占物体价值、物品完好、正点运输和物品错发因素下，采用数据包络分析与模糊综合评价相结合建立第三方物流服务商评价选择模型的过程；文献[4]考虑业务能力、经营管理能力和合作能力三个一级指标，采用改进的AHP法计算各指标的权重，并结合TOPSIS法对各备选方案进行综合评价，通过排序确定各方案的优先级别；文献[5]基于模糊综合评价方法，采用AHP和熵值相结合确定指标权重，通过对信息水平、服务水平、经济因素、运输能力、物流企业形象以及发展潜力的分析，建立了多层次物流服务商的模糊综合评价模型；文献[6]基于模糊综合评判法与灰色关联分析，通过对专家主观排序和模型输出排序进行检验，建立了第三方物流服务伙伴选择模型；文献[7]通过对服务质量、企业实力、成本水平以及合作稳定性的分析，建立了基于三参数区间数群决策的第三方物流服务商选择模型；文献[8]通过对服务水平、技术水平、总体规模以及信誉水平的分析，结合层次分析法、信息熵理论确定各指标权重，建立了模糊综合评判法的第三方物流服务商评价选择模型；

文献[9]为了避免确定权重等主观因素的影响，基于突变理论原理，将模糊数学的隶属函数与突变理论相结合，建立了第三方物流服务商评价选择模型；文献[10]通过客户满意、财务绩效、成本状况和协同发展四个因素的分析，运用熵权法确定指标权重，建立了灰色关联法的物流服务供应链绩效评价模型.

物流服务商的选择是一个复杂的问题，考虑到一般指标权重确定方法的主观性，本文基于信息熵确定指标权重，从服务水平、企业规模、企业信誉以及物流成本四个主要方面建立了物流服务商选择指标体系，并结合余弦决策模型对体系进行了综合评价.

1　物流服务商选择评价体系

1.1物流服务商选择评价指标

随着物流业的快速发展，物流服务商的数量迅速增长，面对众多的物流服务商，企业需要从各方面对服务商进行一个科学合理的选择，其不再是单纯的考察价格和成本，而应该站在供应链战略合作的角度，充分考虑利益共享、风险共担.参考相关文献，结合当今物流服务商自身的特点，从服务水平、企业规模、企业信誉以及物流成本四个主要方面对物流服务商选择进行评价分析，其中服务水平主要考察服务及时性、物品货损率、信息跟踪水平以及顾客满意度；企业规模主要考察信息化程度、财务水平、设备先进性以及行业地位；企业信誉主要考察企业形象、信息共享水平、服务态度以及解决问题时效性；物流成本主要考察基本服务成本和特殊服务成本.具体的物流服务商选择评价指标系统如表1所示：

表1物流服务商选择评价指标体系

1.2评价指标的规范化处理

假设有n个物流服务商可供选择评价，同时由表1可以看出，评价方案的指标个数为m=14，则令tij为方案集n关于指标集m的决策矩阵.考虑到各评价指标属于不同的量纲，为了便于进行综合评价，需要对各指标进行规范化处理.其一般方法为：

成本型指标的标准化函数:

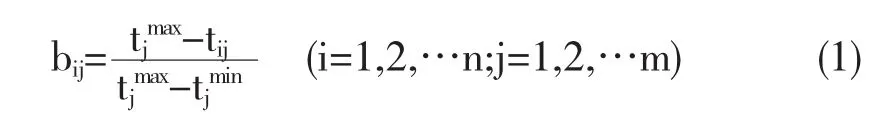
效益型指标的标准化函数:

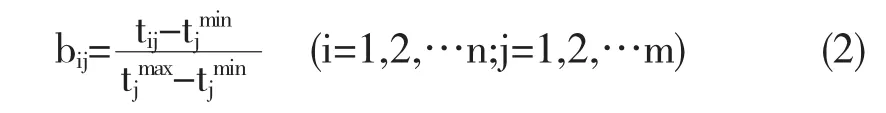
其中记T=(tij)n×m为原始决策矩阵，B=(bij)n×m为规范化后的标准矩阵.

2　基于信息熵的评价指标权重的确定

不同评价指标对评价指标体系的影响程度主要通过权重进行反映，因此如何科学合理的确定各指标权重，关系到整个评价指标体系的评价效率.考虑到物流服务商选择评价因素的不统一性，结合信息熵的相关理论，本文采用熵权法来确定物流服务商选择评价的各指标[11].其具体计算步骤如下：

（1）对标准矩阵B=（bij）n×m进行归一化处理，可以得到归一化矩阵B*=(b*ij)n×m：

（2）计算各评价指标tij的熵值：

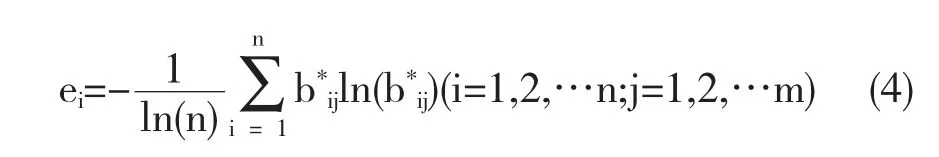
（3）计算各评价指标tij的权重：

3　基于熵权和余弦决策的物流服务商选择模型

3.1余弦决策原理

定义1[12,13]平面坐标系中以原点0为起点，以物流服务商T*在评价指标tj下的值bij为终点dij，构成的有向线段odij(i=1,2,…n;j=1,2,…m)称为物流服务商选择的指标线段，如图1所示：

定义2平面坐标系中以原点0为起点，以最理想的物流服务商T*在决策指标gj下的值dj为终点，构成的有向线段odj(j=1,2,…m)称为物流服务商选择的理想指标线段，如图1所示：

定义3理想指标线段odj和一般指标线段之间的夹角θij(锐角)，称为指标线段夹角，如图1所示：

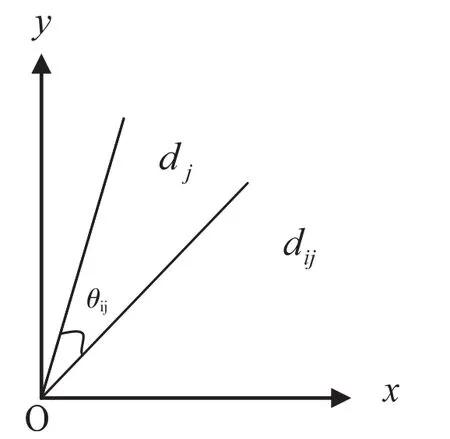
图1指标线段夹角示意图

定义4令集合d=(d1,d2,…dn)，则它的范数值为：

定义5物流服务商Ti=(bi1,bi2,…bim)的指标线段odij与最理想的物流服务商T*=(g1,g2…gm)的指标线段odj的夹角余弦值为：

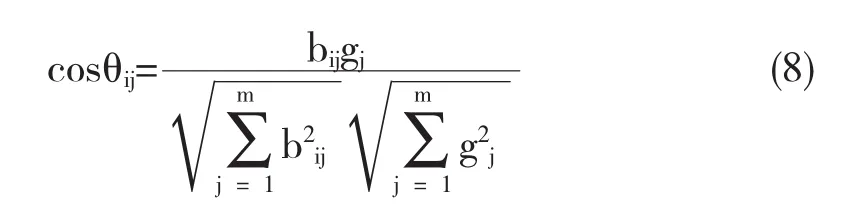
3.2综合余弦值计算及排序

对物流服务商进行选择评价时，物流服务商Ti的单个评价指标tj只能从一个方面对物流服务商本身进行评价，如果要对多个物流服务商进行选择时，则要分别考虑每个物流服务商所有指标tj的综合余弦值，即要结合各评价指标tj的权重进行加权处理.通过信息熵理论确定的物流服务商评价指标权重为wj，从而可以得到物流服务商Ti与理想物流服务商T*之间的综合余弦值为：

其中，Di为物流服务商Ti到理想物流服务商T*的综合余弦值；wj为评价指标tj指标权重向量，cosθij物流服务商T*各指标线段到理想物流服务商T*各指标线段的余弦值.由于0≤cosθij≤1，可知，随着cosθij的增加，物流服务商Ti与理想物流服务商T*之间的指标值越接近，则Di的值也会越大.根据Di的大小即可对各物流服务商的优越性进行排序，Di值越大说明物流服务商Ti与理想物流服务商T*的关联性更强，也即物流服务商Ti最优.因此最优物流服务商Ti的余弦决策模型可以表示为：

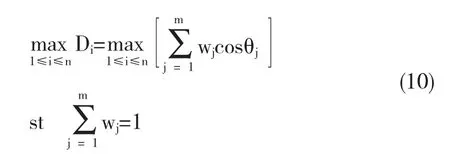
4　算例分析

假设某物流企业在进行业务外包时，有三个物流服务商可供选择，分别为A、B、C.结合物流服务商选择的特点，采用Delphi法从从服务水平、企业规模、企业信誉以及物流成本四个主要方面进行分析，可以得到三个物流服务商选择评价的指标值，如表2所示：

表2物流服务商评价指标因素量化表

4.1熵权法确定指标权重

根据公式（1）、(2)，对三个物流服务商各评价指标进行规范化处理，可以得到各指标规范化后的标准矩阵为：

结合公式（3），即可对标准矩阵B=(bij)n×m进行归一化处理，从而可以得到归一化矩阵为：

再结合公式(4)、(5)、(6)，便可得到物流服务商各评价指标因素tij的权重wi为：

wi=（0.112,0.097,0.067,0.035,0.063,0.057,0.072,0.068,0.056,0.103,0.039,0.059,0.121,0.051）

4.2物流服务商选择余弦值的计算及排序

由物流服务商标准矩阵B=(bij)n×m可知理想物流服务商T*=(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)，则根据公式（8），即可得到物流服务商Ti与理想物流服务商T*之间各评价指标的夹角余弦值如下矩阵所示：

根据余弦决策法的基本理论，由公式（10），可以计算出每个物流服务商各指标综合余弦值Di，其计算如下：

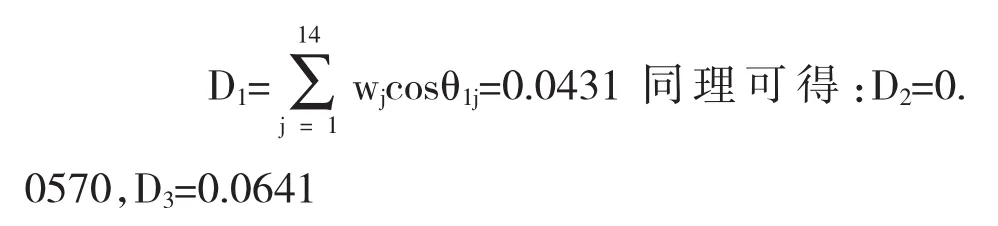
即D3>D2>D1，故物流服务商C的各指标综合余弦值最大，则物流服务商C的优势更强.

由以上分析可知，服务及时性、物品货损率、解决问题时效性以及基本物流服务成本对物流服务商选择的影响比较大，因此物流服务商为了提高服务水平，应该重点考虑时间、质量、成本以及问题解决速度等因素.

5　结论

本研究基于余弦决策法，考虑各指标之间的相互重要性，采用信息熵理论确定各指标权重，从服务水平、企业规模、企业信誉以及物流成本四个主要方面对物流服务商选择进行了综合评价分析.并通过算例分析对模型的科学性和有效性进行了验证.研究结论表明，服务及时性、物品货损率、解决问题时效性以及基本物流服务成本对物流服务商选择的影响比较大，这为物流服务商提高服务水平指出了重点.

参考文献：

〔1〕房士吉.第三方物流服务商评价研究[D].大连：大连理工大学，2010.10-28.

〔2〕刘小兰,等.基于DEA-AHP的农产品物流服务商评价与选择[J].昆明理工大学学报,2013,13(3): 68-72.

〔3〕魏倩.基于DEA与模糊综合评判的第三方物流服务商评价研究[J].社科论坛,2012:215-216.

〔4〕殷秀清,等.基于改进AHP法-TOPSIS法的第三方物流服务商选择[J].技术与方法,2012,2(41): 127-129.

〔5〕秦立公,等.基于模糊综合评价的现代会展物流服务商选择[J].桂林理工大学学报,2012,32(4): 613-617.

〔6〕方春明,等.基于模糊综合评判与灰色关联分析的汽车工业第三方物流服务商平价指标体系[J].吉林大学学报（工学版）,2009,39(1):133-137.

〔7〕龚立雄,等.基于三参数区间数群决策的第三方物流服务商选择方法研究[J].数学的实践与认识,2014,44(2):57-63.

〔8〕俞峰,等.基于熵权模糊层次分析法的大型体育赛事第三方物流服务商评价与选择[J].贵州体育科技,2013,3(9):4-6.

〔9〕王勇,等.基于突变理论的第三方物流服务商优选方法[J].商业研究,2009,8(7):148-150.

〔10〕霍红,等.基于灰关联熵的物流服务供应链绩效评价[J].物流工程与管理,2012,34(219):67-70.

〔11〕何满辉,等.基于信息熵多属性决策的物流供应商选择评价[J].工程设计学报,2013,20(1):6-10.