能量平衡法静电驱动柔性振膜微泵特性分析*

胡院林，梁　鑫，王　文，张　彧（上海交通大学机械与动力工程学院制冷与低温研究所，上海200240）



能量平衡法静电驱动柔性振膜微泵特性分析*

胡院林，梁鑫，王文*，张彧
（上海交通大学机械与动力工程学院制冷与低温研究所，上海200240）

摘要：从能量平衡的角度建立了静电驱动柔性振膜微泵的平衡方程，基于对压缩过程中振膜动能的考虑，改进了最小能量法压缩模型，结合均匀压力载荷下圆薄膜大挠度形变理论对静电驱动柔性振膜微泵进行理论分析。对振膜与腔体壁面贴合的压缩过程中各能量相互转化的关系进行分析，并与最小能量法模型进行了对比。结果表明，能量平衡法考虑了薄膜振动过程中的动能，故薄膜与腔体具有更大的贴合面积，且以薄膜与腔体完全贴合时作为零应力参考状态降低压缩过程中的薄膜形变势能，计算得到的静电微泵的压缩效率更高，在驱动电压为300 V时，改进的双腔模型中振膜贴合半径为4.06 mm，所得最大压升为87.08 kPa。基于改进的模型，对双腔微泵压升的影响因素进行讨论，发现降低柔性薄膜厚度会使输出压力有所上升，并且减小腔体表面介电层厚度、减小腔体深度与半径可以有助于提高微泵的压升。

关键词：静电驱动微泵；能量平衡法；柔性薄膜形变

微驱动器作为微机电系统的核心部件，一直在MEMS领域内受到极大的关注。目前研究较多的微驱动器有压电驱动器，电磁驱动器，静电驱动器和形状记忆金属驱动器［1］，其中无阀压电微泵的研究最为广泛［2-3］，但受限于压电材料形变较小，输出压力有限。静电驱动器由于具有能量密度高、响应时间短、能量消耗低等特点，使静电驱动微泵广泛应用于生物流体控制、环境检测、电子器件热管理、微型制冷［4］等领域。常见的静电微泵由腔体、含有电极的膜片和控制流体进出的阀门等部件组成。

Bonghwan Kim［5］对平行板式静电驱动柔性薄膜微泵进行了研究，在柔性薄膜从一端向另一端贴合的过程中，实现了流体的运输。Mathew B［6］基小挠度弹性形变和热力学分析建立了平板式方形和圆形薄膜振动压缩模型，并讨论了腔体内余隙容积对压缩特性的影响。Shannon［7］首次提出渐进式腔体结构替代平行板式腔体结构，并采用柔性薄膜振子结构，大大提高了静电微泵的压缩性能。Saif［8］采用最小能量法建立了单腔回转曲线结构的静电驱动柔性振膜微泵理论，但是在分析振膜形变时忽略了振膜的周向应力，使振膜形变偏大。李丽伟［9］利用瑞利-黎兹能量法进行静电弹性耦合分析，计算出微泵弹性振子的谐振频率。Sathe A A［10］采用有限分割法通过力学平衡建立了双腔微泵压缩模型，并采用实验数据间接对其模型进行了论证。陈荣［11］基于最小能量法建立了双腔微泵压缩模型，结果表明双腔结构腔体可以有效抑制薄膜的形变，从而提高微泵压升。张彧［12］等人将柔性振膜大挠度形变半解析解［13］应用到振膜形变理论分析中，结果表明薄膜形变半解析解具有更高的精度。

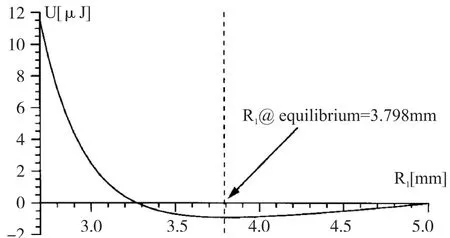
图1　单腔微泵能量随薄膜贴合半径变化曲线

从能量的角度去分析静电驱动柔性薄膜微泵压缩过程可以直观地反映出微泵的运行机制，以期分析出提高微泵压缩效率的方法。一般而言，该微泵在周期性压缩流体过程中，主要实现静电能、压缩流体做功、薄膜应变能和薄膜动能之间的相互转化。图1为微泵压缩过程中各总能量随柔性薄膜贴合半径的关系曲线。文献［6，9-10］采用最小能量法分析了微泵的压缩过程，最小能量法的物理意义是当微泵中能量（忽略薄膜动能）处于最小值时，振膜达到平衡点，为压缩的终止点，即图1 中A点所示状态。而该状态对应于微泵压缩过程中的受力平衡状态，理想条件下该点是振膜动能达到的最大值状态。对于周期性振动的薄膜，其受力平衡点并不是压缩过程中的终止点，对于微米尺度的微泵结构，各能量量级非常小，振膜在振动过程中的动能会对最终的压缩终止状态产生一定的影响。根据能量转化，振膜在压缩过程中的最终点应该是其动能为零的点，不考虑能量散失的情况下，在压缩最远点，静电能完全转化为柔性薄膜的弹性势能和克服压缩流体所做的功。

根据能量最小法物理意义可知，其描述的是静电驱动微泵单次压缩过程中静止平衡的位置，而不是周期性的往复压缩过程中所能达到的最大点。文献［10-11］都是从受力平衡的角度去描述静电压缩过程，然而单次压缩过程的平衡点并不能反应周期性振动压缩过程的最大压缩点。目前很少有文献针对静电微泵压缩过程中的能量变化对其进行建模分析，本文从能量的角度出发，结合柔性薄膜大挠度形变理论，通过能量平衡法建立微泵压缩过程中压升模型，将薄膜周期性压缩过程中的动能考虑在系统总能内，认为在压缩终止态时，静电功完全转化成薄膜形变势能和压缩流体做功，即图1中B点所对应状态为周期性压缩过程中最大压升点。此外，陈荣［11］等人的双腔结构模型中，以振膜水平状态作为其形变势能零点，使得振膜在压缩过程中产生的形变势能较大，减小了静电力功转化成压缩流体功的效率。本文设定当振膜与一侧腔体完全贴合时为形变势能零点，可以通过降低振膜压缩过程中的形变势能的方法提高微泵的压缩效率，故在本模型中振膜在水平位置处于松弛态。基于改进的模型，讨论了薄膜厚度与微泵腔体参数对压升的影响。

1　静电驱动柔性振膜微泵建模

双腔结构微泵可以明显提高被压流体的压升［11］，故本文直接针对双腔结构静电驱动微泵进行建模分析。静电驱动柔性振膜理论分析模型包括均匀压力作用下的圆薄膜大挠度形变半解析解和能量平衡法两方面。如图2所示，静电驱动柔性振膜微泵主要由腔体和振膜组成。柔性薄膜的表面为金属电极层，腔体表面为介电层，防止在薄膜贴合过程中出现电流短路。当流体从进气阀进入腔体后，振膜在静电力的驱动下与腔体逐渐贴合，实现压缩过程，当腔体内的流体达到一定的压力时打开排气阀，将流体排出腔体。当排气阀打开时，柔性薄膜在静电力的驱动下逐渐向中心贴合，使被压流体以恒定的压力输送出腔体，然后转换电极极性，开始另一侧的压缩过程。由于振膜的一侧在压缩流体的同时，另一侧处于进气状态，故双腔结构可以有效提高压缩流体的流量。

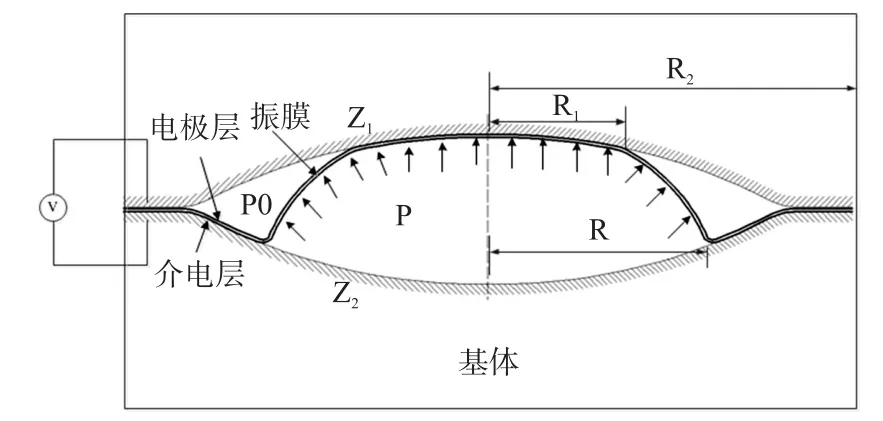
图2　双腔振膜微泵示意图

针对理论上的分析和计算，有必要对模型进行一些基本假设：①柔性薄膜各向同性，并且相关物理特性均匀分布。②薄膜厚度远小于其直径，相变过程中弯曲应力可以忽略，厚度保持不变。薄膜在初始条件下处于松弛状态，不存在初始应力。③在柔性薄膜压缩贴合过程中遵循等温压缩［10］，并且忽略压缩过程中压膜阻力。

1.1柔性圆薄膜大挠度形变半解析解

如图3所示，圆薄膜在一定的气体压力下，会产生相应的形变，该形变量决定振膜的在压缩流体过程中的弹性势能，并与流体压力耦合决定最终压缩状态。针对双腔微泵中的柔性薄膜，虽然在压缩过程中，会与另一侧腔体壁面贴合，但未贴合的部分仍然需要通过薄膜形变解析解计算获得。

设薄膜在均匀压力P的作用下的挠曲线放程为ω(r)，根据受力分析可得圆薄膜大挠度控制方程为：

其中Nθ，Nr分别是薄膜周向和径向应力。周向与径向的应变和位移之间的关系为

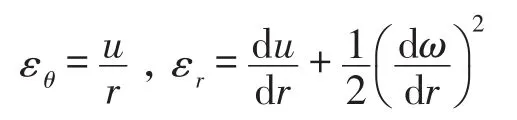
图3　均匀压力下柔性圆薄膜变形

柔性薄膜在形变过程中的四周固定，故在边界处的挠度和位移均为0，引入无量纲参数，则控制方程转化为，

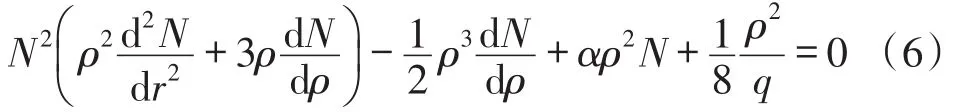
通过边界条件可得，

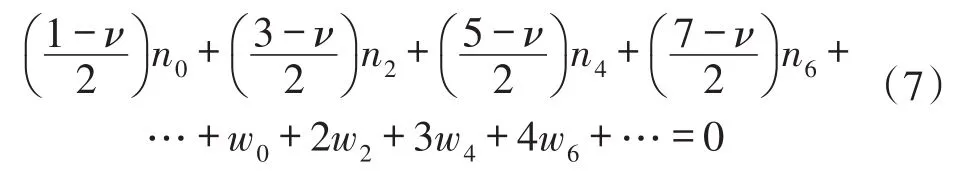
通过方程（7）可得n0值，从而可得圆薄膜大挠度形变的半解析解。在压力为600 Pa时，初始应变为0.044的条件下，其计算结果与Stanford B等人［14］的实验数据对比发现，该半解析解公式获得的挠度与实验测量误差仅为1%。在薄膜厚度为25 μm，壁面介电层厚度为11 μm，初始压力在1 kPa的条件下，将薄膜形变解析解的中心挠度与Sathe A A［10］的实验数据进行对比，如图4所示，结果表明最大误差为8%，由此可知柔性薄膜大挠度解析解具有足够高的精度计算微泵腔体中薄膜形变。

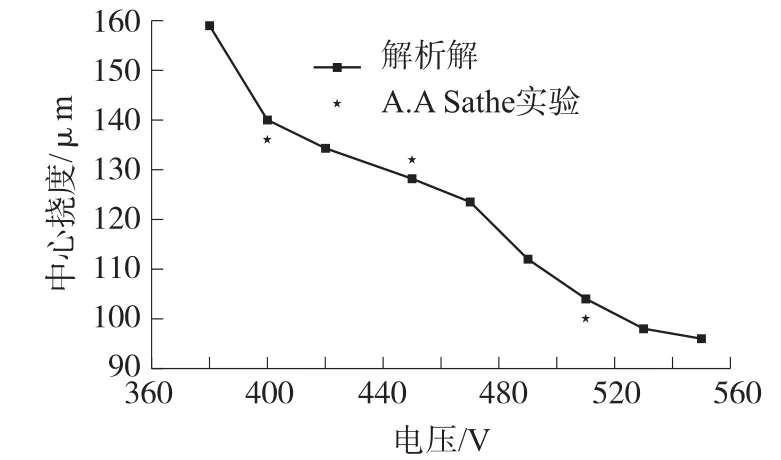
图4　大薄膜形变解析解与实验对比

1.2能量平衡法

渐进式腔体在交流电压的激励下，驱动柔性薄膜从外围向中心贴合，在贴合的过程中，以静电力作为驱动力，带动薄膜形变，达到压缩流体的目的，实现多场耦合。在薄膜达到最大压缩点时，打开排气阀，排出压缩流体，完成单次压缩循环过程。根据压缩过程中的能量转化，当薄膜动能为零时达到压升的最大状态，故在该微泵达到该状态时开启排气阀门，完成单次压缩。文献［10-12］在计算双腔微泵薄膜弹性势能时，将柔性薄膜的初始态设定为水平状态，但是双腔微泵在连续压缩过程中，初始状态应从完全与一侧腔体贴合时开始，故应将薄膜与腔体完全贴合时的状态设定为应力和应变为零点的状态，从而减小压缩过程中薄膜的弹性势能，提高静电能与流体压力能之间的转化效率。

设振膜压缩过程中无能量散失，则微泵在压缩过程中始终有静电能、流体的获压缩功、薄膜弹性势能和薄膜动能之间的相互转化。设初始态为从振膜完全贴紧上腔体时开始，压缩过程中的能量始终有如下关系：

其中，Ee表示静电力做功，Ecom表示克服压缩流体所做功，ΔEmem表示压缩过程薄膜弹性势能变化量，ΔEk表示压缩过程中薄膜动能变化量。由于微泵的尺度非常小，能量量级较小，薄膜的动能也会对压升产生影响，故在确定最远压缩点时，应考虑振膜动能对压缩终态的影响。理论上易知，当薄膜压缩到最远点时，动能为零，故Ee=Ecom-ΔEmem。

根据saif［8］等人的研究结果，腔体与贴合薄膜之间的电容能远大于未贴合的薄膜部分，故在计算腔体与薄膜之间的电容能，只需要考虑贴合部分的电容能。对于电容板静电力做功，根据静电力做功特点，其值与板间的电容能相等，其中，ε0为真空介电常数，k为介电层的相对介电常数，d为介电层厚度，Va为驱动电压，Ae为薄膜与腔体的贴合面积，为腔体半径，R为静电力驱动下薄膜贴合半径。

振膜应变能为振膜能量密度全体积的积分，其计算公式为：

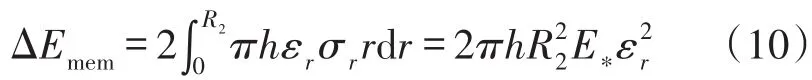
其中，h为薄膜厚度，E∗=E/(1-υ2)，相对压缩初始状态的振膜应变，其中r2为薄膜与上腔体贴合半径，

根据假设，流体在被腔体内的被压过程是等温压缩过程，故压缩流体做功为，

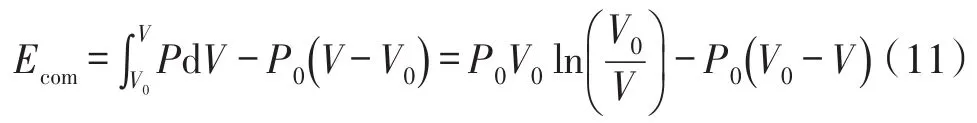
其中，V0是腔体总体积，V是压缩终止时薄膜与腔体所围体积。设Z1(r)，Z2(r)分别是腔体上下壁面函数，故双腔初始体积为，V0=2∫0R2πr(Z1-Z2)dr。R1为上腔体贴合半径，薄膜与腔体所围的体积为：

当流体被压流体达到压升最大值时，ΔEk=0，故在不考虑能量散失的情况下有，Ee-Ecom-ΔEmem=0成立，结合式（9）~式（11）可以确定压缩终点时薄膜与腔体的贴合半径以及压升特性。

2　模型计算结果与对比讨论

模型采用聚酰亚胺柔性薄膜，其厚度为13 μm，弹性模量为G=2.47×109Pa。腔体的半径R2=5 mm，腔体最大深度为100 μm（c=4），其表面介电层厚度0.4，相对介电常数K=3。腔体内外的初始压力P0=5×105Pa，真空介电常数ε0=8.85×10- 12C2/Nm2。微泵驱动电压变化范围100 V~300 V。图5是双腔微泵压缩过程流体过程中柔性薄膜的贴合半径与腔内压升之间的关系。在驱动电压为300 V的条件下，计算可得柔性薄膜压缩终止位置如图6所示，下腔体贴合半径R=4.06 mm。

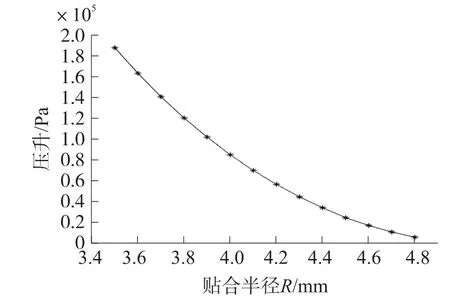
图5　微泵压升与贴合半径关系曲线

图6　压缩终止薄膜贴合状态

2.1不同模型计算结果对比

图7对比了不同压缩模型计算所获得的压升。Saif［8］以及Sathe AA［10］分别采用最小能量法和有限分割法分析了单腔微泵压升特性，通过对比发现双腔微泵可以有效提高微泵压升特性。张彧［12］模型在计算双腔微泵压升时，初始体积按照单腔结构公式计算，故获得的压升偏低。通过与陈荣［11］等人工作对比发现，能量平衡法计算所得压升稍高于最小能量法计算所得压升，其原因是能量平衡法将压缩过程中薄膜的动能计入压缩总能中，在300 V的驱动电压下，采用能量平衡法计算的压升比最小能量法高出约10 kPa，说明振膜动能可进一步使柔性膜发生形变和压缩流体，从而造成腔内流体压力进一步增加。

图7　不同模型计算结果

在驱动电压为300 V的条件下，振膜与腔体贴合过程中的总能量（f）、静电能（Eelec）、压缩能（Ecom）和薄膜形变能（Emem）随振膜贴合半径的变化曲线如图8所示，其中（a）是以柔性薄膜在水平时为零应力状态，（b）是以柔性薄膜与腔体完全贴合时为零应力状态。由图知，在薄膜由四周向中心贴合过程中，总能量先增大，然后迅速降低，因为静电能的增长速度在贴合面较大时远小于压缩流体耗能的增长速度。根据图8（a），当贴合点在A1点时，贴合半径为4.15 mm，静电能完全转化为压缩流体做功与振膜弹性势能，达到压缩的最远点，压升为78.32 kPa，陈荣［11］在相同条件下采用最小能量法计算出振膜平衡状态，贴合半径为R=4.31 mm，获得压升为P=69 kPa，对比发现，由于最小能量法所描述的为单次压缩的静态平衡过程，忽略了薄膜的动能，故其薄膜贴合面小，获得较小压升。由图8（b）中的能量曲线知，将柔性薄膜与腔体完全贴合时作为零应力参考状态时，微泵最大贴合半径R=4.06 mm，压升为P=87.08 kPa，对比发现，通过降低压缩过程中的薄膜形变能，可以有效提高静电能压缩流体的效率。

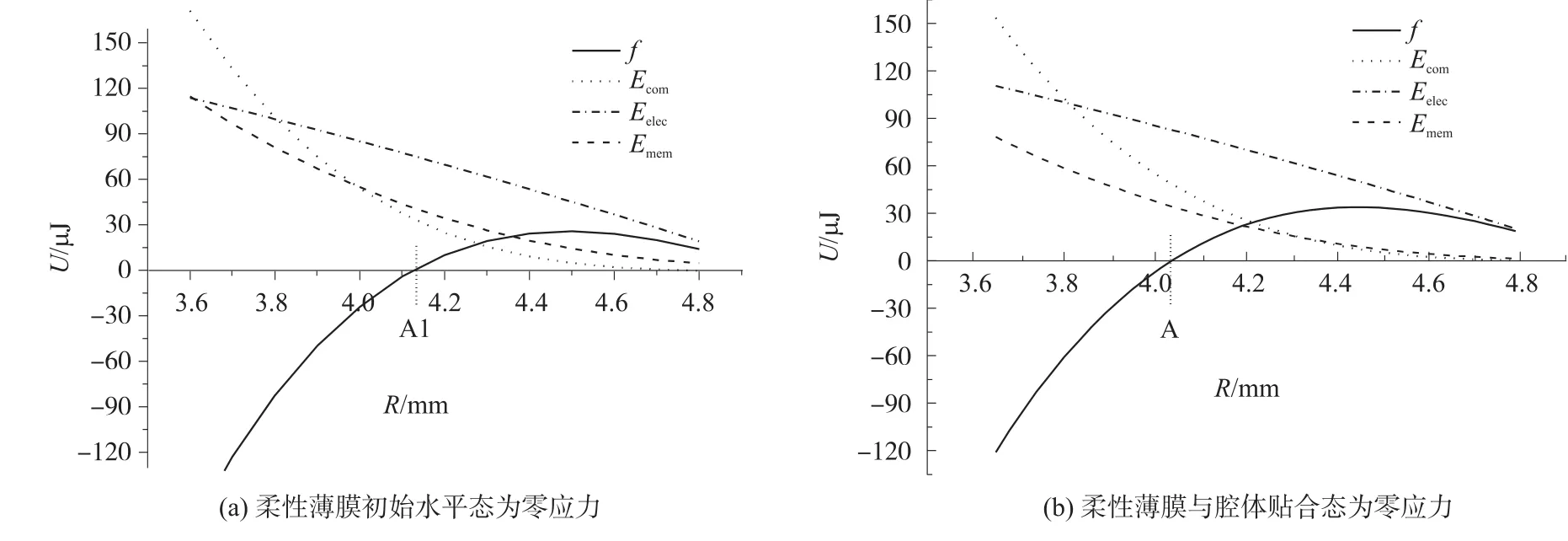
图8　薄膜贴合过程中各能量变化关系曲线

2.2不同参数对微泵压升的影响

基于改进的压缩模型，讨论柔性薄膜厚度、腔体深度与半径和腔体介电层厚度、双腔结构对微泵压升的影响。图9表示振膜厚度变化对微泵的压升性能的影响。

图9　薄膜厚度对微泵压升的影响

从图9可以看出，随着薄膜厚度的降低，相同驱动电压下，压升会略有增加，主要原因是薄膜厚度的降低会减少振膜的形变能，根据能量守恒，减小的能量转化成流体压缩功，提高腔内流体的压升，故对静电驱动柔性微泵来说，在技术允许范围内，尽可能采用薄的柔性膜。

图10为不同腔体深度与半径对微泵压升的影响。从图10（a）中可以看出，保持腔体半径不变，随着腔体深度从150 μm降到50 μm过程中，振膜与腔体的贴合面积逐渐增大，这使得流体压力上升。腔体深度减小一倍时，微泵压升增加了近两倍。但是由于腔体深度的降低，腔体体积减小，在驱动频率不变的条件下，单程压缩所获得的压缩流体流量也会降低，故应根据流体流量与压升综合选定腔体深度。同理，如图10（b）所示，腔体深度不变时，腔体半径从10 mm降低到5 mm的过程中，微泵压升增加非常明显（约2倍），但相应的单次压缩的流体量也随之下降。

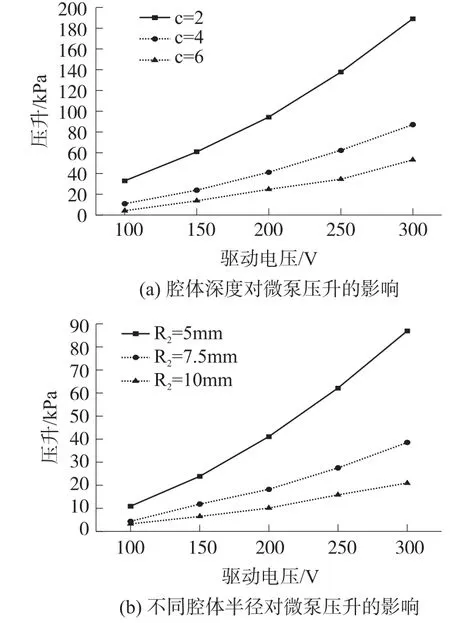
图10　不同腔体深度和半径对微泵压升的影响

图11为腔体表面介电层厚度对微泵压升的影响。从图中可以看出，介电层厚度的降低可以有效增加微泵的压升，在300 V的驱动电压下，保持其他条件不变，介电层厚度从0.4 μm降到0.2 μm时，压升提高了近一倍，并且随着电压的升高，增加的百分比越高，该结果与文献［8，12］中的分析结果具有一致性。

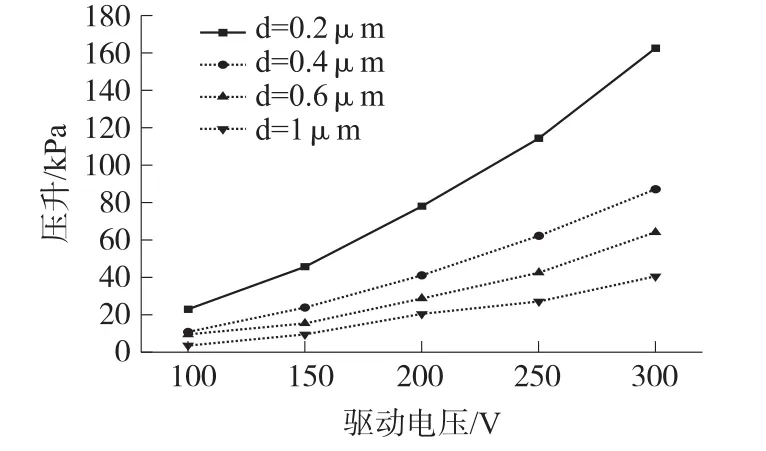
图11　介电层厚度对微泵压升的影响

3　结论

本文基于能量平衡法结合柔性薄膜半解析解对双腔结构微泵的压缩特性和能量转化关系进行了研究，并讨论了相关参数对静电微泵压缩特性的影响。结论如下：①基于对压缩过程中振膜动能的考虑，采用能量平衡法获得的微泵压升高于最小能量法获得的压升。并且设定柔性薄膜与腔体完全贴合时为初始零应力态，可以有效提高静电能压缩流体的效率。在驱动电压为300 V的条件下，对于改进的静电微泵模型，薄膜贴合半径为4.06 mm，可获得最大压升为87.08 kPa，较相同条件下最小能量法模型压升高10 kPa。②相同驱动电压下，使用厚度较小的振膜，可以显著提静电微泵压升。不考虑微泵流量变化时，当腔体半径和腔体深度分别减小一倍时，微泵压升分别增加了近两倍。同时，降低腔体表面介电层厚度，也可以有效增大微泵的压升。

参考文献：

［1］许忠斌，杨世鹏，刘国林，等.微泵的研究现状与进展［J］.液压与气动，2013（6）：7-12.

［2］王蔚，田丽，鲍志勇，等.一种新型压电式双向无阀微泵的研制［J］.传感技术学报，2006，19（5）：2018-2021.

［3］崔琦峰，刘成良.串联压电微泵特性研究［J］.传感技术学报，2006，19（5）：1974-1982.

［4］Suwat Trutassanawin，Eckhard A Groll，Suresh V Garimella，et al. Experimental Investigation of a Miniature-Scale Refrigeration Sys⁃tem for Electronics Cooling［J］. IEEE Transactions on Compo⁃nents and Packaging Technologies，2006，29（3）：678-687.

［5］Bonghwan Kim. Electrostatically Driven Single Chamber Bidrec⁃tional Peristaltic Gas［J］. Journal of the Korean Physical Society，2010，57（6）：1494-1499.

［6］Mathew B，Hegab H. Analytical modeling of microscale diaphragm compressors［J］.Applied Thermal Engineering，2013（51）：130-136.

［7］Shannon M A，Philpott M L，Miller N R，et al. Integrated meso⁃scopic cooler circuits（IMCCS）［C］//ASME International Mechani⁃cal Engineering Congress and Exhibition，Advanced Energy Sys⁃tem Division，1999：75-82.

［8］Saif M T A，Erdem Alaca B，Huseyin Sehitoglu. Analytical Model⁃ing of Electrostatic Membrane Actuator for Micro Pumps［J］. IEEE Journal of Microelectromechanical Systems，2008，8（3）：335-344.

［9］李丽伟，朱荣，周兆英.基于能量法的微驱动器静电弹性耦合分析［J］. MEMS技术与器件，2006（5）：244-246.

［10］Abhijit A Sathe，Eckhard A Groll，Suresh V Garimella. Analytical model for an electrostatically［J］. Journal of Micromechanics and Microengineering，2008（18）：035010（11pp）.

［11］陈荣，王文.静电驱动柔性振模型微泵的动力学分析［J］.工程热物理学报，2010，31（2）：197-200.

［12］张彧，王文，赵小林，等.静电驱动振模微泵的理论分析［J］.传感器与微系统，2013，32（1）：25-29.

［13］Marianna Coelho，Deane Roehl，Kai-Uwe Bletzinger. Numerical and Analytical Solutions with Finite Strains for Circular inflated Membranes Considering Pressure—Volume Coupling［J］. Interna⁃tional Journal of Mechanical Sciences，2014（82）：122-130.

［14］Stanford B，Ifju P.The Validity Range of Low Fidelity Structural MembraneModels［J］.ExperimentalMechanics，2008（48）：697-711.

胡院林（1991-），男，安徽芜湖人。上海交通大学在读博士，主要从事微型动力机械与高效热管换热研究工作，huyuan⁃lin65@sjtu.edu.cn；

王文（1967-），男，新疆人，博士，上海交通大学机械与动力工程学院教授，博士生导师，研究方向为微型制冷技术与微型动力机械、热力过程优化与联供技术、低温两相流、热管、高效换热器与电子设备热控制。主持参加多项国家科学自然基金，国家973项目等，wenwang@sjtu.edu.cn。

Fabrication and Analysis of Low Power Micro Fluxgate*

LÜ Hui1，2*，LI Suiyuan3
（1.Electrical Engineering and Automation institute，Henan Polytechnic University，Jiaozuo He’nan 454000，China；2.School of Electronics and information，Northwestern Polytechnical University，Xi’an 710129，China；3.Science and Technology institute，Jiaozuo Teachers College，Jiaozuo Henan 454000，China）

Abstract：To meet the low power consumption demand，the micro fluxgate based porous core was designed and fab⁃ricated by MEMS technology. Porous thin film core can be effectively used to decrease the power consumption and improve the performance of sensor. By comparing the influence of the aperture ratio of porous core on the exciting current，the optimal parameters are obtained. This parameter can meet the requirement of performance of sensor and meanwhile the requirement of preparation process.

Key words：porous core；micro fluxgate；MEMS；lower power

doi：EEACC：3120W，7230M10.3969/j.issn.1004-1699.2016.01.004

收稿日期：2015-07-28修改日期：2015-10-05

中图分类号：TH38

文献标识码：A

文章编号：1004-1699（2016）01-0015-06

项目来源：国家自然科学基金项目（50976067）；国家自然科学基金项目（51576123）