基于电流纹波率反激式变压器导通模式的分析*

周有平，陈国杰，李　斌（佛山科学技术学院理学院，广东佛山528000）



基于电流纹波率反激式变压器导通模式的分析*

周有平，陈国杰*，李斌
（佛山科学技术学院理学院，广东佛山528000）

摘要：提出了利用电流纹波率设计反激式变压器和判别其导通模式的方法，用该方法导出了反激式变压器从CCM进入DCM模式的数学式，用MATLAB计算并分析了输入电压、负载电流及反射电压对导通模式的影响。计算表明，最小电流纹波率或反射电压取值越大，反激变压器在输入电压增大或负载电流减小时越容易进入DCM模式。设计了一款24 V 1.5 A反激式开关稳压电源，测量了变压器的电流波形。实验表明，测量结果与推导的数学式相符，用电流纹波率设计反激式变压器比传统的波形系数更直观和便于测量。

关键词：反激式变压器；电流纹波率；导通模式；分析

项目来源：国家自然科学基金（61178030）

反激式变压器以其电路简单、成本低等优点，广泛应用于150W以下的开关电源中［1-5］。根据电流是否连续，反激变压器分为连续导通模式（CCM）、断续导通模式（DCM）和临界导通模式（BCM）3种［6］。其中CCM模式的峰值电流比DCM模式小、开关管损耗小、效率高，故大功率反激式变压器多采用CCM模式，尽量避免进入DCM模式。但是，宽输入电压CCM模式反激式变压器的设计较困难，因为它在满载和低输入电压时工作于CCM模式，在轻载和高输入电压时又会工作于DCM模式［6］；并且，至今未见文献给出输入电压和负载使反激式变压器从CCM模式进入DCM模式的数学式。此外，反激式变压器通常采用电流波形系数来进行设计和分析，即定义波形系数KRP=变压器初级纹波电流/初级峰值电流，以表征反激变压器是工作于连续模式（KRP<1）还是工作于非连续模式（KRP>1），以及用KRP来设计反激变压器［4-7］。由于变压器的初级峰值电流没有初级平均电流容易测准，故通过KRP用初级平均电流换算得到［4-7］，这显然没有DC-DC变换器用电流纹波率（定义为变压器初级纹波电流/初级平均电流［8］）来设计电感那样直观和易于测量。本文阐述反激式变压器的电流纹波率，利用电流纹波率导出反激式变压器从CCM模式进入DCM模式的数学式，用MATLAB计算并分析输入电压、负载电流和反射电压对反激式变压器导通模式的影响。用低功耗、高性价比的PWM控制芯片OB2263设计一款24 V、1.5 A反激式开关稳压电源，测量不同条件下反激变压器的电流波形，并与推导的数学式进行比较。

1　反激式变压器的电流纹波率

设反激变压器工作于CCM模式，输入直流电压为Vin，反射电压为VOR，开关频率为f，周期为T，开关管导通时间为ton，变压器初级绕组电感为L，则占空比为［8］

D通常小于0.5。这一方面是因为D较小时，VOR较小，开关管应力小，成本低，另一方面变压器匝比较小，漏感较小。图1（a）、1（b）是反激式变压器CCM模式的初级和次级绕组的电流波形。图1（c）是将次级电流等效到初级后合成的电流波形［8］，类似于Buck-Boost变换器的连续电流波形，因此可采用Buck-Boost变换器的电流纹波率来设计反激式变压器和判别其导通模式。

图1　反激变压器电流波形

反激式变压器的纹波电流为

设反激式变换器的输出功率为Po，效率为η，则输入平均直流电流为

变压器初级绕组电流波形的斜坡中心电流为

将式（2）除以式（4），并将式（1）代入，得初级绕组电流的纹波率为

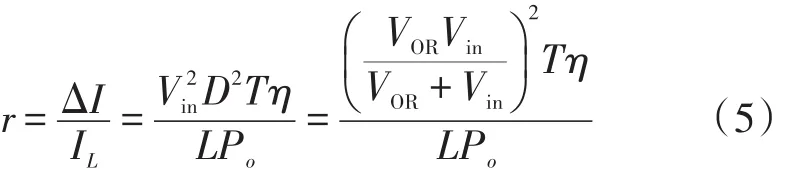
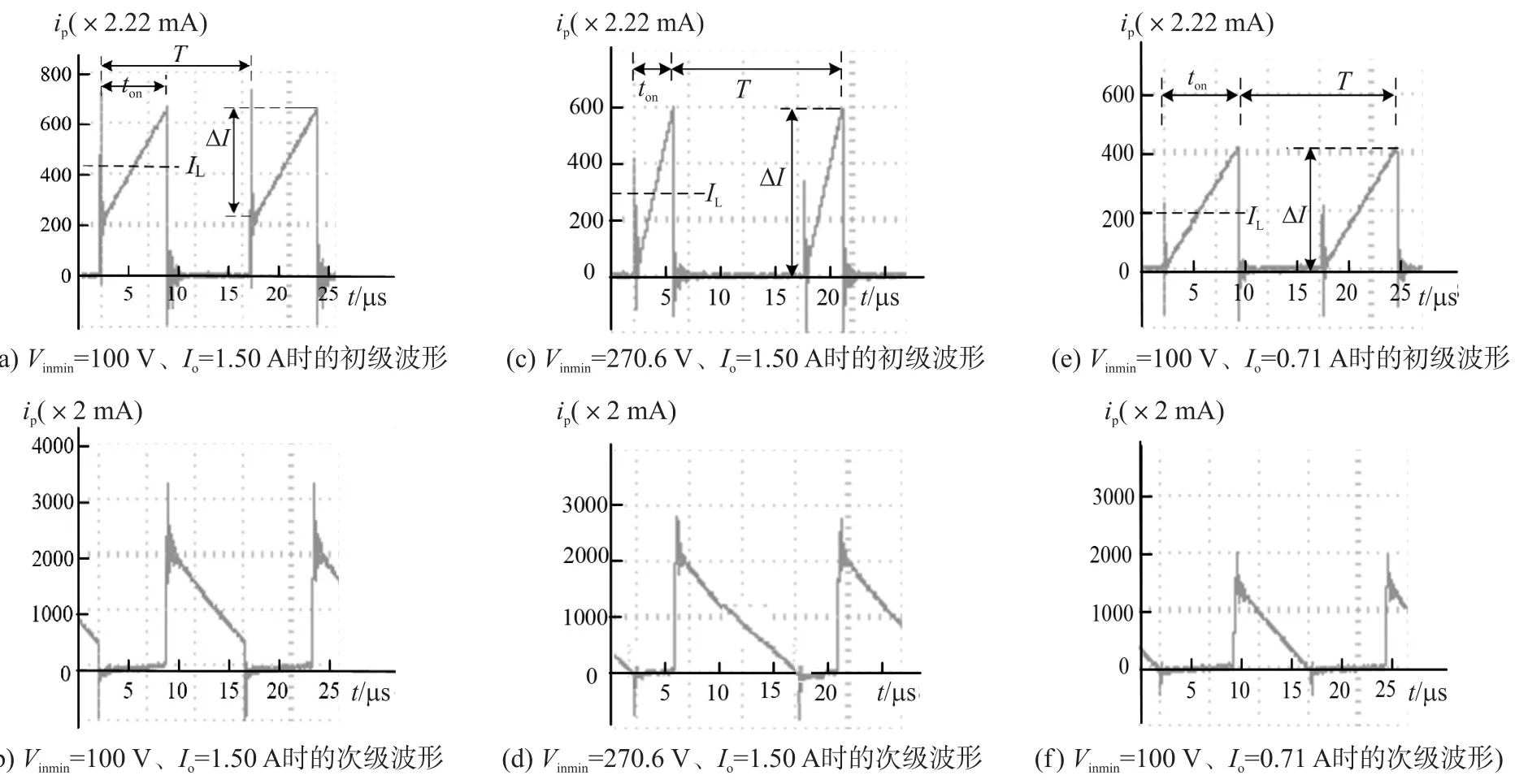
式（4）表明，Vin、Io和VOR取值对r有较大影响，其变化可使变压器从CCM模式进入DCM模式。与Buck-Boost变换器一样，反激式变压器在CCM模式0

在最大负载功率Pomax给定后，对于输入电压在Vinmin~Vinmax宽范围内变化的反激式变压器，由式（4）知，当Vin=Vinmin时，电感电流最大，故称Vinmin为最恶劣输入电压。通常，在Vin=Vinmin条件下设计变压器的初级电感，此时r为最小值rmin，D为最大值DMAX。由式（1）和式（3）得

对于PWM稳压的反激式变换器，Vo不变，则Pomax=Vo×Iomax。设变换效率η不变，则式（5）除以式（7）得

依据式（8），可分析反激式变压器的Vin、Io和VOR对反激变压器导通模式的影响。

2　Vin、Io、VOR和rmin对反激变压器导通模式影响的分析

对于交流输入电压为85 V~265 V的变换器，通常取Vin min=100 V，Vin max=375 V。变压器初始工作于CCM模式。

2.1当Io=Io max时，Vin、VOR和rmin对导通模式的影响

设Vinmin=100 V、对应的rmin=0.4（CCM模式时r最佳值［8］），则根据式（8）用MATLAB计算并绘出VOR= 80 V、150 V和310 V时r随Vin的变化曲线，如图2曲线a、b、c所示。由图可见，r随Vin增大而增大；VOR越大，r增加得越快，变压器越容易进入DCM模式。

考察极端情况，rmin=0.4不变，设Vin=Vinmax=375 V时变压器进入BCM模式，此时r=2，则由式（8）得VOR=306 V。这表明，只要VOR<306 V，不论Vin在100 V~375 V范围内如何变化，变压器一直工作于CCM模式。在实际设计中，VOR一般小于150 V，所以在满负载条件下，Vin变化不会改变该变压器的CCM模式。作为例子，取极端值VOR=310 V，则r=2对应的Vin=371.8 V（图2曲线c的Q点），相当于交流输入电压263 V，已远大于220 V交流输入电压，故满负载时该变压器在宽输入电压范围工作于CCM模式。

图2　r随Vin变化的计算曲线

作为比较，设Vinmin=100 V、对应的rmin=1（CCM模式），由式（8）绘出VOR=80 V时r随Vin的变化曲线，如图2曲线d所示。此时r=2对应的Vin=293.5 V（图2曲线d的P点），比rmin=0.4的Q点Vin低78.3 V，表明rmin越大，变压器在Vin增大时越容易进入DCM模式。

2.2当Vin不变时，Io和rmin对导通模式的影响

设VOR=80 V、rmin=0.4，则根据式（8）用MATLAB绘出Vin=100 V或375 V时r随Io的变化曲线，如图3所示。由图可见，r随Io的减小而增大；Vin越大，r就越大，越容易进入DCM模式。

考察最小输入电压即Vin=Vinmin=100 V情况，设Io减少到IOBCM时进入BCM模式，此时r=2，由式（8）得Io=IOBCM=0.2Iomax（图3曲线a的A点）。这表明，当Vin=100 V时，只要Io大于0.2Iomax，变压器就可一直工作于CCM模式；此时CCM模式的负载电流变化率DIo/Iomax=（Iomax-0.2Iomax）/Iomax=80%。考察最大输入电压即Vin=Vinmax=375 V情况，将r=2代入式（8）得IOBCM=0.44Iomax（图3曲线b的B点）。这说明，当Vin= 375 V时，只要Io大于0.44Iomax，变压器就可一直工作于CCM模式；此时CCM模式的负载电流变化率DIo/Iomax=（Iomax-0.44Iomax）/Iomax=56%，比前面Vin=100 V时负载电流的变化率小24%。这是因为，由式（1）知，在VOR不变条件下，Vin就越大，占空比D就越小，变换器通过调节D来进行PWM稳压时允许Io变化的范围就越小。作为比较，设Vinmin=100 V、对应的rmin=1，由式（8）绘出的r随Io变化曲线如图3曲线c所示。此时r=2对应的Io=IOBCM=0.5Iomax（图3曲线c 的C点），比rmin=0.4的A点Io=0.2Iomax高0.3Iomax，表明rmin越大，变压器在Io减小时越容易进入DCM模式。

图3　r随Io变化的计算曲线

3　实验与讨论

采用低功耗、高性价比的PWM控制芯OB2263设计一款24 V、1.5 A反激式稳压电源，设计参数为：直流输入电压Vinmin=100 V，Vinmax=375 V，开关频率f=60 kHz，Pomax=Vo×Iomax=24 V´1.5 A=36 W，η= 85%，rmin=1、VOR=80 V。将rmin、VOR代入式（7），算得反激变压器的初级电感L=0.75 mH。变压器磁芯选EE2825，Ae=86 mm2，取ΔB=0.25 T，材质为PC40，初级NP=52匝，次级NS=16匝，匝比n=NP/NS=3.25。电路如图4所示，图中给出了元件的实际参数。

图4　实验用24 V、1.5 A反激式稳压电源电路图

用图4电源进行实验，负载RL采用0~40 W可调150 W无感绕线电阻，用交流调压器调节输入电压，用数字万用表UT58E测量Vin及Vo、Io，用泰克TDS1002C-EDU 60 MHz示波器先测量R5的电压波形，再除以0.45 W即乘以2.22得到初级电流波形；在次级绕组中串接1∶100电流互感器，电流互感器接50 W电阻，先测该电阻的电压波形，再乘以100除以50 W即乘以2得到次级电流波形。当Vin=Vinmin=100 V，调节RL使Io=1.50 A时，测得Vo=24.01 V，变压器初级和次级绕组的电流波形如图5（a）、5（b）所示。由图可见，开关管Q导通时，变压器初级电流线性增大到峰值，次级电流为零，磁芯储存能量；开关管Q截止时，初级电流为零，次级电流从峰值线性减少，磁芯释放能量。电流波形的前、后沿均有尖峰和振铃，这是在开关管Q导通或截止瞬间变压器漏感所致。次级电流为梯形波且最小电流大于零，说明变压器工作于CCM模式。实验测得，T=16.2 ms，f=1/T=61.7 kHz，r= DI/IL=1，与电源的设计值吻合。测得D=ton/T=7.1/ 16.2»0.44，将Vin=100 V、VOR=80 V代入式（1）算得D» 0.44，D测量值与理论值在误差范围内吻合良好。这说明，测量数据较准确。由于变压器的初级平均电流比峰值电流容易测准，且可通过不涉及纹波系数的简单关系式（4）与反激式变换器的输入平均直流电流之间建立联系而进行理论比较，故利用电流纹波率来设计反激变压器和判别其导通模式的方法比传统的波形系数更直观、便于测量。

图5　反激变压器电流波形

保持负载RL不变，当Vin逐渐增大时，观察到变压器的初级和次级电流波形的占空比变小，纹波率逐渐变大。当Vin=270.6 V时，次级电流波形在开关管截止期结束时刚好回到零，如图5（c）、5（d）所示，测得r=DI/IL=2，表明变压器此时工作于BCM模式。将Vinmin=100 V、VOR=80 V、Io=Iomax=1.50A、rmin=1、r=2代入式（8），算得r=2对应的Vin=293.8 V，如图2曲线D的P点，与实验测得的Vin=270.6 V相差7.9%，两者较一致；这偏差主要来自BCM模式电流波形的观测误差。测得D=ton/T=3.9/16.2»0.24，将Vin=270.6 V、VOR=80 V代入式（1）算得D»0.23，D测量值与理论值基本相等。同时，测得Vo=24.02 V，Io=1.51 A，表明所设计的反激式开关电源的输入特性良好。保持Vin= Vinmin=100 V不变，减小RL使Io逐渐减小时，观测到变压器初级和次级的电流波形的峰值下降，纹波率逐渐变大，占空比不变，这是因为Vin和VOR没变，由式（1）知D不变。当Io=0.71 A时，次级电流波形在开关管截止结束时刚好回到零，如图5（e）、5（f）所示，表明此时变压器工作于BCM模式。将Vin=Vinmin、rmin=1、r=2代入式（8），得r=2对应的Io=Iomax/2=0.75 A（图2曲线c的C点），与实验测得的Io=0.71 A相差5.3%，吻合良好。同时，测得Vo=24.02 V，表明所设计的反激式开关电源的稳压性能优良。

4　结论

本文将反激式变压器等效为Buck-Boost变换器，提出了利用电流纹波率设计反激式变压器和判别其导通模式的方法，用该方法导出了输入电压、负载电流和反射电压使反激式变压器从CCM模式进入DCM模式的数学式。MATLAB计算表明，rmin或VOR越大，反激变压器在Vin增大或Io减小时越容易进入DCM模式；在满负载及rmin=0.4条件下，只要VOR<300 V，不论Vin在100 V~375 V范围内如何变化，反激变压器可一直工作于CCM模式。用PWM控制芯片OB2263设计了一款24 V、1.5 A反激式开关稳压电源，测量了不同条件下反激变压器的电流波形。实验表明，测量结果与推导的数学式相符，用电流纹波率来设计反激变压器和判别其导通模式比传统的波形系数更直观和便于测量，适用于所有反激变压器电感的设计和导通模式的判别。

参考文献：

［1］彭云华，黄土荣，廖晓文，等.反激式开关电源变压器的设计［J］.电子设计工程，2014，22（9）：107-112.

［2］徐列群，杨武，肖恒兵.基于反激变压器的LED恒流电源设计［J］.中国照明电器，2013，（3）：5-9.

［3］张巧杰，熊鸣，祁鲲.两路单端电流反激式开关电源设计［J］.北京信息科技大学学报，2011，26（4）：35-39.

［4］胡志强，王改云，王远.多路单端反激式开关电源设计［J］.现代电子技术，2013，36（14）：162-170.

［5］赵祥，方方，马柯帆，等.基于TOP261YN芯片的多路输出单端反激式开关电源的设计［J］.核电子学与探测技术，2010，30 （11）：1529⁃1532.

［6］杜琰琪，范鹏飞，凌有铸，等.单端反激式开关电源中变压器的设计［J］.工业控制计算机，2012，25（3）：101-105.

［7］周党培，陈业仙.一种实用的反激开关电源变压器设计方法［J］.四川兵工学报，2011，32（8）：96-98.

［8］Sanjaya Maniktala. Switching Power Supplies A to Z［M］. Singa⁃pore：Elsevier，2006：137-138.

周有平（1972-），男，广东中山，实验师，本科，主要从事光电子及LED技术实验教学及研究，zypfs@21cn.com；

陈国杰（1965-），男，湖南祁东，教授，博士，本文通信作者，主要从事光电子及LED技术研究，chengj126@126.com。

Design of a High Precision Thermal-Shutdown Circuit*

TAN Yulin，FENG Quanyuan*
（Institute of Microelectronics，Southwest Jiaotong University，Chengdu 611756，China）

Abstract：Based on UMC 0.25 μm BCD technology，a high precision thermal-shutdown circuit is proposed. The temperature detection is achieved by using the negative temperature characteristic of transistor’s base-emitter volt⁃age of bandgap reference. The hysteresis temperature is produced by adjusting the ratio of resistance to avoid the phenomenon of thermal oscillation. By simulation and verification with HSPICE，the thermal-shutdown output re⁃verses to shut down the chip when the temperature reaches 130℃，and return to normal working when the tempera⁃ture drops to 99℃. The amount of hysteresis temperature is 31℃. The thermal shutdown threshold and hysteresis temperature have a maximum drift error of only 0.24℃when supply voltage changes.

Key words：thermal-shutdown；BCD；hysteresis；thermal oscillation

doi：EEACC：7320R；720010.3969/j.issn.1005-9490.2016.01.018

收稿日期：2015-04-03修改日期：2015-05-09

中图分类号：TM46

文献标识码：A

文章编号：1005-9490（2016）01-0081-05