最优潮流在电力系统中的最新应用综述

贵州大学电气工程学院　成　峰



最优潮流在电力系统中的最新应用综述

贵州大学电气工程学院成峰

【摘要】随着电力系统的不断发展，最优潮流问题在电力系统规划、运行、控制等领域有着极为重要的意义。它的目标是在满足一定等式和不等式约束前提下寻求该电力网控制变量的最优设定值，以达到一个或多个目标函数的最优化。本文主要从大规模交直流电网最优潮流和稳定约束最优潮流两个方向总结了最优潮流的最新应用。

【关键词】最优潮流；HVDC；TSCOPF；内点法；辛算法

1　引言

最优潮流(Optimal Power Flow, OPF)是电力系统规划、运行和控制的核心问题。它的主要目标是在满足一定等式和不等式约束前提下找到该电力网控制变量的最优设定值，以达到一个或多个目标函数的最优化。本文重点总结了电力系统最优潮流的最新应用，体现了国内外最新的研究动态。

2　最优潮流的最新应用

2.1大规模交直流电网最优潮流

由于我国客观存在能源资源和电力需求的大跨度分布情况，迫使我国实施“西电东送、南北互供、全国联网”的电力发展战略。超高压电网承担了大范围远距离输送电力的功能。而HVDC因为其传输距离长、线路造价低、线损少、不存在稳定问题、可实现非同步联网等优点，在我国得到大规模应用。包括HVDC模型的潮流计算、OPF着力于对电网规划运行评估以及提高经济效益，是目前的热点之一。

目前最优潮流计算中广泛采取的HVDC模型大多来自文献，其模型忽略了换流阀压降和有功损耗以及换流变压器功率损耗。因为国内采取的HVDC系统传输功率大，采取简化模型已经无法满足工程中的精度要求。文献[1]给出HVDC系统的准稳态模型，准确计及了换流阀和换流变压器上的损耗，并采取交直流系统交替求解的方法进行潮流计算，对交流系统采取标幺值计算，对直流系统采取有名值进行计算。文献[2]将该模型进行恰当的简化和标幺化处理，建立准确的含HVDC的最优潮流模型，并且采用罚内点法(penalty interior point method，PIPM)求解含HVDC最优潮流模型。其中的优化变量包含任一节点的有功、无功出力，无功补偿出力，电压幅值与相角以及直流变量。目标函数则取总有功出力最小。

文献[2]经过算例得出PIPM 能在正常运行电压约束下找到最优解，原因是：对应松弛量相当于在每一个节点增加了可调度负荷、发电机以及容许对母线电压约束先进行松弛，PIPM 在这个迭代过程中逐步驱动松弛量趋于0。

然而大型交直流输电网网损优化也是另一热点。交直流并联电网的网损优化与传统无功优化有着很大区别，纯交流电网主要通过合理配置系统无功用来降低网损，而交直流并联电网则是通过调节直流功率改变有功潮流的分布，并将其转移至交流通道，从而实现降低全网网损。现在区域特高压交直流联网已经是电网发展的重要方向。研究交直流电网网损优化理论具有十分重要的实际应用价值。

文献[3]以南方电网为实例，其主网交直流通道送电水平超过20000MW，厂站无功配置的主要目标是保持通道电压和提高系统稳定性，就目前来说采用交直流调整能够给出的降损空间最为明显。

调节直流输送功率具有调节速度快、灵活等优点，因此大多用来改变系统潮流分布。然而，在调整直流功率时，做到保持各断面不越限，保持电厂出力和各地区送受电计划不变。交直流电网网损优化问题的数学模型如下：是直流系统网损；

2.2稳定约束最优潮流

稳定约束最优潮流是电力系统运行与控制决策中的重要研究内容，其在最小化系统运行成本的同时，能够通过调整稳态运行点，来提升系统受扰后的动态性能，包括暂态稳定性和短期电压稳定性。最近几年，为了维持电力系统在发生故障后的稳定，学者们将动态安全约束整合到常规OPF计算当中，从而构成了暂态稳定约束最优潮流(TSCOPF)，其同时考虑到了电力系统的动态安全性和经济性，成为了一个研究热点。

数学上TSCOPF问题在是一个含有微分代数方程约束的非线性规划问题。由于含有微分方程，所以无法直接应用到常规的数学优化方法当中。

国内外学者提出了一些新的数值积分方法，从而为求解TSCOPF问题提供了新的方向。我国著名的数学家冯康提出了的针对哈密尔顿系统的辛几何算法，简称辛算法。由于电力系统的具有庞大冗杂的特性，有学者提出了改进哈密尔顿系统辛几何方法的建议。辛Gauss-Legendre Runge-Kutta(GLRK)方法是其中的一种，该方法是单步隐式方法，其计算精度高，数值稳定性好。有的将转子运动方程变换成哈密尔顿正则方程的形式，采取四阶辛GLRK的方法离散化该方程，确立了辛GLRK方法的TSCOPF哈密尔顿数学模型。然而在同样的精度下条件，四阶辛GLRK方法的步长是隐式梯形法的6倍。采用的TSCOPF模型，以有功网损最小为目标函数，其表达式为：

现代内点算法在电力系统中得到了广泛的应用。但是，当系统规模庞大，其计算时间就会迅速延长，内存也将大量消耗，所以为了使得求解效率提高，可以采用减空间技术求解修正方程。原始–对偶内点法与减空间技术相结合能够大大提高求解大规模TSCOPF问题的效率。

目前基于时域仿真信息的EEAC法，用于量化系统的暂态稳定性，已经应用在实际电网安全稳定量化评估的方法中。有文献采用基于单机等值技术来进行暂态稳定评估，稳定性用稳定裕度和灵敏度来量化，这种方法能够有效解决TSCOPF问题。也有采用等值后的功角门槛值约束与最优潮流结合，其计算相对简便，但是存在系统稳定性不能采用功角门槛值来量化评估的问题。

文献[5]采用的是将TSCOPF问题划分为最优潮流、灵敏度分析和暂态稳定评估三个问题来迭代求解。最优潮流问题采用非线性原对偶内点法来求解，包括简单稳定约束最优潮流。各稳定裕度的控制变量灵敏度通过轨迹灵敏度法来求解。暂态稳定评估采用EEAC法，同时得出不同稳定情况下的裕度表达式。然后添加矫正因子来避免过度调整，以达到稳定和经济的协调。

基于EEAC理论等值后的模型为：

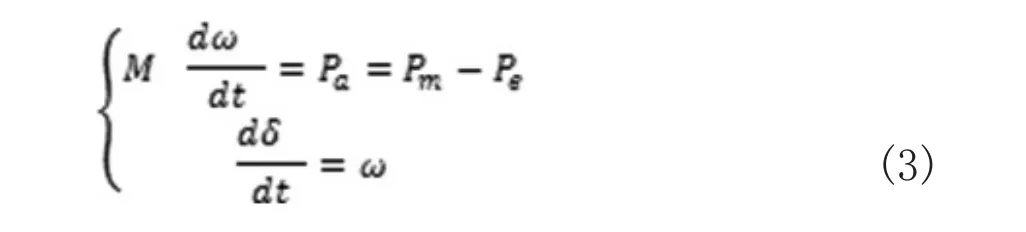
采用轨迹灵敏度能够很好地分析系统参数对系统动态性能的影响，其包含的轨迹灵敏度方程与暂态时域仿真方程相仿，都是DAE方程，但是将轨迹灵敏度方程进行差分化之后就是线性方程，其可以提高求解速度，并且还可以进一步采用并行技术。文献[5]采用的方法，综合考虑了系统在不同稳定情况下通过调整来提高系统稳定裕度，从而实现暂态稳定约束的最优潮流计算，使得系统经济运行。同时也考虑到了多摆失稳情况以及解决不同失稳模式下的多故障问题。

3　结语

最优潮流有着广泛的应用场景，根据不同的应用场景，拓展不同的数学模型，比如更换部分约束条件和目标函数。随着电力工业的发展，现代电网的规模和运行复杂程度日趋增加，最优潮流或许将作为一个子问题或者子模块，通过设计一个大的迭代框架，选取合理的最优潮流算法，实现更复杂的问题，然而，最关键的问题将是如何高效而精确的求解最优潮流。

参考文献

[1]郑超,盛灿辉,郭小江,等.实用高压直流输电稳态模型及潮流算法解析[J].电网技术,2011,35(3):57-62．

[2]郑华,李晖,肖晋宇,等.大规模交直流电网最优潮流模型与算法研究[J].中国电机工程学报,2015,35(9): 2162-2165.

[3]刘恺,陈亦平,张昆,等.大型交直流并联输电网网损优化理论及其在南方电网中的实现[J].中国电机工程学报,2014,34(1):130-135.

[4]刘鹏飞,韦化,李滨,等.基于哈密尔顿系统与辛算法的暂态稳定约束最优潮流[J].电网技术,2015,39(5): 1329-1334.

[5]赵晋泉,钱莉,陈刚.一种基于EEAC和轨迹灵敏度的暂态稳定约束最优潮流模型与方法[J].电力系统保护与控制,2015,43(9):9-12.

成峰（1989－），男，硕士研究生，研究方向为电力系统安全稳定与控制。

作者简介：