捷联成像导引头视线角速率提取方法与仿真分析
2016-03-22西南技术物理研究所姚秀娟王宏宇李力文
西南技术物理研究所 姚秀娟 王宏宇 李力文
捷联成像导引头视线角速率提取方法与仿真分析
西南技术物理研究所姚秀娟王宏宇李力文
【摘要】本文以工程应用为出发点,对捷联成像导引头视线角速率的提取及滤波方法进行了有条理的叙述。建立模型进行仿真并对仿真结果进行了分析。
【关键词】捷联;视线角速率;滤波
1 概述
捷联成像导引头结构上与弹体固连,使其失去了直接测定视线角速率的能力,只能测量目标相对于弹体的体视线角。捷联成像导引头测量的体视线角中包含了目标相对惯性空间的视线角和弹体运动两部分信息,制导系统要实现制导律则必须将导引头测量信号中耦合的弹体运动信息去除,提取出目标相对惯性空间的视线角及角速率。
2 坐标系定义及其转换
目标视线角速率解算中用到的坐标系有:地理坐标系Oxeyeze、弹体坐标系Oxbybzb、视线坐标系Oxsyszs、体视线坐标系Oxlylzl。其中,θ为弹体姿态俯仰角, Ψ为弹体姿态偏航角,γ为弹体姿态滚动角,qλ为视线方位角,qγ为视线高低角,qβ为体视线方位角,qα为体视线高低角。以上各定义及坐标系之间的转换关系见文献[1]。
3 视线角速率解算
在捷联导引头中,导引头传感器可测得体视线高低角qα、体视线方位角qβ,要求取视线高低角qγ、视线方位角qλ转动的角速度qγ和qλ。
根据文献[1]中坐标系定义,目标在体视线坐标系和视线坐标系中的位置坐标均为( R 0 0),则目标在体坐标系以及地理坐标系中的坐标分别为:

又根据关系:
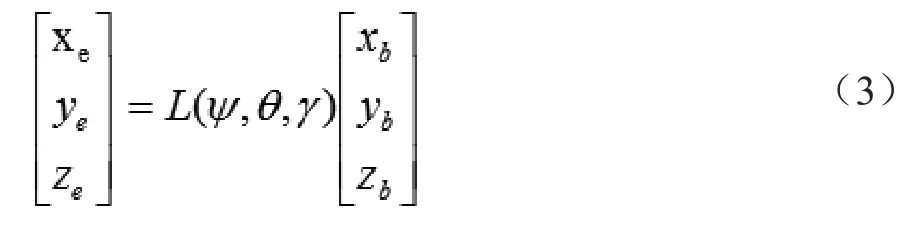
得:

可得:


其中:

式(5)(6)即为捷联成像导引头系统目标视线角解耦算法。文献[1]中根据目标视线角、体视线角及其微分利用个坐标系之间的推导关系求取目标视线角速率。为了避免体视线角微分误差在复杂的计算中被放大。本文将qγ和qλ进行微分直接得到目标在地理坐标系的俯仰视线角速度和方位视线角速度。这种方法简化了计算过程,提高运算速度。
4 捷联成像导引头仿真
4.1仿真模型建立
在工程应用中,捷联成像导引头已知条件为弹上陀螺测得的弹体坐标系下的弹体角速度Ωx、Ωy、Ωz和导引头传感器测得的体视线高低角qα、体视线方位角qβ。要求取视线高低角qγ、视线方位角qλ转动的角速度qγ和qλ。
根据弹体坐标系与地理坐标系的转换关系,推导出Ωx、Ωy、Ωz与弹体姿态角的关系。[2]
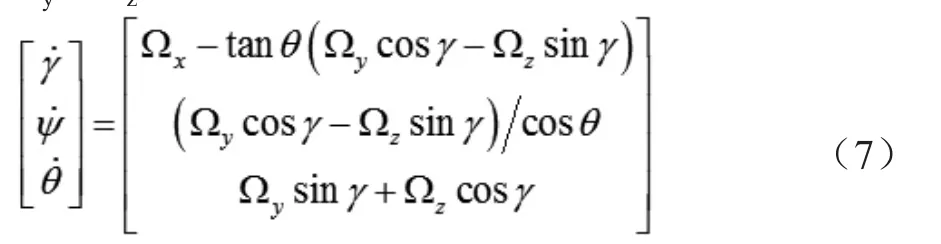
(7)式为方向余弦矩阵,对以上方程进行积分,可得弹体相对于地理系的三轴姿态θ、Ψ、γ。
仿真时要构造体视线角,实际应用此数据由探测器测量。体视线高低角qα、体视线方位角qβ的构建方法:对设定的目标视线角速度进行积分,再根据(4)式进行推理计算。

图1 系统仿真simulink模型图

图2 弹体扰动下的视线角速度仿真结果
搭建的系统整体Simulink仿真模型如图1所示。
4.2仿真结果及分析
输入条件及仿真结果如图2所示。
分析以上仿真结果可知:当弹体滚动通道存在周期扰动时,若目标视线角不断增大,则求解得出的目标视线角速率逐渐发散;若目标视线角逐渐收敛,则目标视线角速率仿真结果也逐渐收敛。理论上,不考虑测量误差时,目标视线角速率的仿真值应与视线角速率输入的理论值完全一致,视线角速率仿真结果波动发散的原因是由于仿真模型中存在离散微分环节,微分模块通过对目标的体视线角进行微分得到目标的体视线角速率,并以此进一步推算的出目标视线角速率,而离散微分环节存在计算误差和相位延迟问题,该误差直接导致求解的目标视线角速率波动发散,该过程具体分析如下:
若目标视线角逐渐增大,由于滚动通道周期波动的耦合,目标相对于弹体的体视线角也逐渐增大,并且体视线角的波动幅值也越来越大,此时对体视线角进行离散微分时,由于体视线角波动越来越大,离散微分产生的误差亦越来越大,推算得出的视线角速率就会有发散的趋势;同理,若目标视线角逐渐减小,目标相对于弹体的体视线角亦逐渐减小,滚动通道耦合产生的体视线角波动逐渐减小,此时对体视线角离散微分产生的误差也逐渐减小,解算得出的视线角速率呈现出收敛的趋势。
4.3视线角速率滤波
以上算法仿真分析没有考虑传感器件测量噪声,仅分析了算法在理想测量条件下的仿真结果,对算法的正确性进行了验证分析。然而实际过程中需考虑导引头的测量噪声,且捷联式导引头测量噪声极为严重,因此需对解算得到的视线角速率进行滤波。相关文献中介绍的多为卡尔曼滤波方法,[3]卡尔曼滤波计算复杂且需要知道噪声的方差,而在实际工程应用中很难知晓测量噪声的具体情况。
本文采用平均滤波与低通滤波组合的滤波方式进行仿真,仿真条件如下。

图3 视线角速率平均滤波仿真结果
弹体姿态扰动角速率取为:

视线角速率理论值:
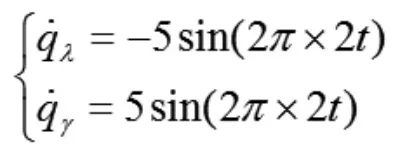
微分环节时间常数:。
使用平均滤波器仿真结果如图3所示。
根据以上仿真结果可见,在假定的视线角速率及导引头测量噪声条件下,对解算得到的视线角速率不进行滤波时,基本不能分辨出视线角速率的变化趋势;对比分别采用3点、5点、7点、10点进行平均滤波所得结果可知,采用数据点越多,仿真得到的视线角速率受测量噪声影响越小,曲线越平滑,但相位滞后也越严重。
使用低通滤波器和平均滤波的仿真结果如图4所示。
引入低通滤波器后,增强了系统对高频噪声的抑制能力,从仿真结果可以看出,与未采用低通滤波器所得结果相比,对于采用同样的滤波方法,采用低通滤波器所得结果曲线更为平滑,但低通滤波器存在相位滞后,滞后时间增加。
5 结论
本文从工程应用的角度对视线角速率的提取方法和仿真结果进行了分析,为了提高滤波效果且尽可能减小时间滞后,应合理选择递推平均滤波数据点数及选择合适的低通滤波器时间常数和微分环节时间常数。参考文献
[1]李璟璟.捷联成像导引头视线角速率估计方法研究.国内图书分类号: TP751.
[2]周瑞青.捷联导引头稳定与跟踪技术[M].国防工业出版社.2010.8.
[3]姚郁,章国江.捷联成像制导系统的若干问题探讨[J].红外与激光工程.2006年2月第35卷第1期.
姚秀娟(1980-),女,硕士研究生,高级工程师,研究方向:导引头稳定伺服控制。
作者简介:
