一点法经验数优化方法在HD海域气田的应用研究

藤赛男，李元生

（1. 中国石油化工股份有限公司上海海洋油气分公司勘探开发研究院，上海 200120；2. 中海石油（中国）有限公司上海分公司研究院，上海 200030）

一点法经验数优化方法在HD海域气田的应用研究

藤赛男1，李元生2

（1. 中国石油化工股份有限公司上海海洋油气分公司勘探开发研究院，上海 200120；2. 中海石油（中国）有限公司上海分公司研究院，上海 200030）

HD海域已开发气田实施了大量回压试井和一点法试井。利用陈元千经验数或通过对实施过回压试井的气井取经验数的平均值作为气藏经验数来预测气井无阻流量，平均误差均超过20%。鉴于此，此文以无阻流量误差最小为目标，建立一点法经验数优化方法。通过对该海域X和Y气藏研究发现，X气藏和Y气藏最优经验数分别为0.083和0.15，无阻流量平均误差分别为4.3%和15%，比常规方法分别减小27.7%和40%。此研究可一定程度提高一点法产能评价的精度，对于提高一点法产能评价方法在气田的适应性具有一定的意义。

一点法产能评价；经验数；最优化方法

一点法产能评价方法只要求测取地层压力、一组稳定流压及稳定产量，便可确定气井产能，对于探井而言，可以大大缩短测试时间，减少气体的放空和节约费用，减少资源浪费[1-14]。一点法产能评价是否准确的关键在于经验数α的获取，陈元千教授[9]首次根据我国16口气井经验数α的平均值得到气藏的经验数α = 0.25。而其他众多学者研究一点法产能评价时，同样是统计各自气田多口井经验数的平均值作为气田的经验数来进行产能评价，不同气田得到的经验数如表1所示。

由表1统计结果可知，上述气田的经验数α的取值与陈元千统计的经验数（等于0.25）差异很大。并且利用算术平均方法得到的经验数计算出的无阻流量，与气井实际无阻流量相比，其误差未必是所有经验数中最小的[8]。为提高一点法产能评价的精度，本文提出一点法经验数优化确定方法。

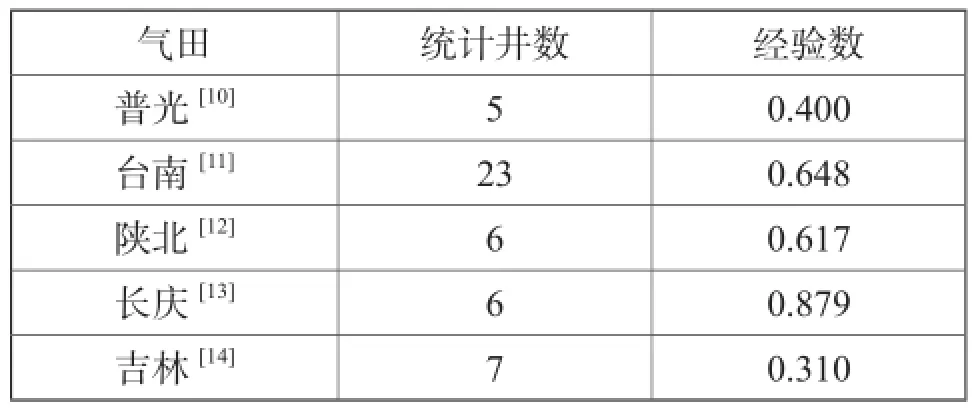
表1 不同气田经验数

1 一点法经验数优化研究

目前产能评价方法有一点法产能试井和多点法产能试井（回压试井、等时试井或修正等时试井），通过对多点法产能试井资料进行优化处理，可以得到适合一点法产能评价方法的经验数。假设有n口井实施了多点法产能试井，则利用如下步骤得到一点产能评价方法的最优经验数：

（1）获得气井实际无阻流量。对气井多点法产能试井资料进行回归得到气井产能方程系数A、B和无阻流量，并计算对应井的经验数：

( qAOF1, α1)；( qAOF2, α2)；…( qAOFi, αi)；…( qAOFn-1, αn-1)；( qAOFn, αn) （1）

（2）优选一组井底流压和产量。利用步骤（1）中的经验数计算多点法测试中每个工作制度下的无阻流量，与步骤（1）中无阻流量比较，从中优选出使得无阻流量误差最小的一组井底流压和产量：

( pwf1, qsc1)；( pwf2, qsc2)；…( pwfi, qsci)；…( pwfn-1, qscn-1)；( pwfn, qsnn) （2）

（3）获得经验数αi下的无阻流量。给定一个经验数αi和步骤（2）中的流压和产量代入到一点法公式中得到气井无阻流量：

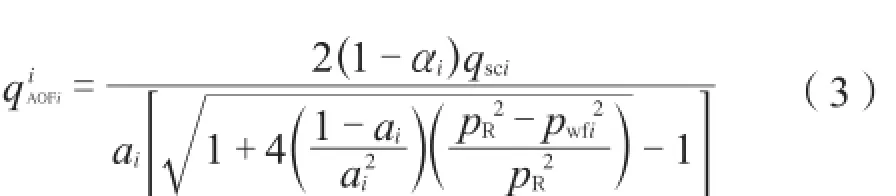
（4）统计经验数αi下无阻流量。利用步骤（3）中的方法，得到经验数αi下对应井的无阻流量：

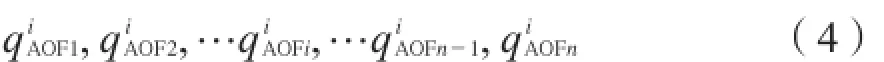
（5）计算经验数αi下无阻流量平均误差和均方差。通过步骤（1）中气井实际无阻流量和步骤（4）中利用经验数计算的无阻流量对比，得到统计井的无阻流量平均相对误差和均方差：

（6）建立经验数αi与无阻流量平均相对误差和均方差的关系。取不同经验数αi重复步骤（3）～（5）得到不同经验数下的无阻流量平均相对误差和均方差：

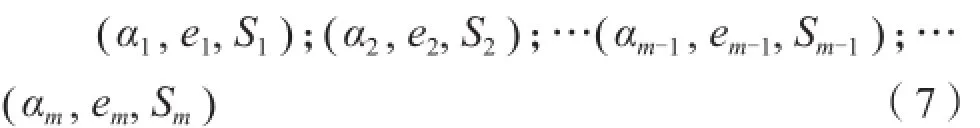
其中：0≤αj≤1，i =1, 2 … m，且当i＞j时，αi＞αj。

（7）利用上述方法可以得到不同经验数下的气井无阻流量平均误差和均方差，通过最小二乘法或者绘图法，可知存在经验数αe= α ( emin)使得气井无阻流量平均相对误差最小，即：

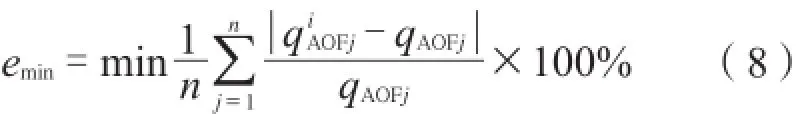
也存在经验数αS= α ( Smin)使得气井无阻流量均方差最小，即：

（8）比较αe和αS，如果两者基本相等，并且emin和Smin都较小时，说明一点法产能评价方法在气田上应用误差较小，其最优经验数为：

（9）若αe和αS数值相差较大，则利用经验数计算的无阻流量与气井实际无阻流量相差较大，一点法产能评价方法在气田上应用误差较大，不适合一点法经验数来计算产能。

2 应用及效果分析

HD海域X气田与Y气田投产至今实施了多次多点法试井，故可以利用常规一点法经验数和本文方法获得气藏最优经验数来评价气井产能。

2.1 X气田

X气田从2011～2015年实施了9次产能测试，其产能方程、无阻流量和经验数如表2所示。

表2 X气田多点法产能试井数据表

从表2可知，9口井平均经验数为0.2，该经验数和陈元千经验数下气井无阻流量的相对误差如图1所示，经验数为0.2时无阻流量误差为14% ～ 50%，平均误差为32%；陈元千方法（经验数为0.25时）无阻流量误差为20% ～ 70%，平均误差为45%。下面对适合HD海域凝析气藏的产能评价方法进行研究。

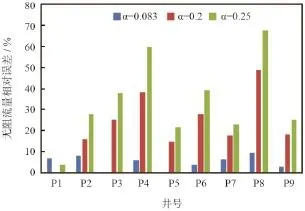
图1 X气田气井无阻流量相对误差直方图

首先从每次测试数据中优选一组产量和井底流压，然后利用最优化方法获得X气田的经验数。以P1井为例，优选出一组产量和井底流压数据，该井的产能试井曲线如图2所示。

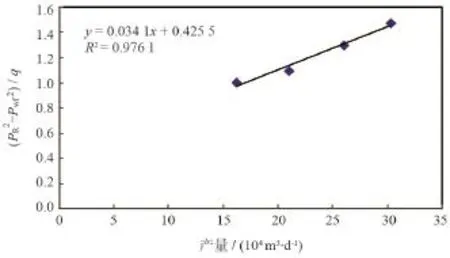
图2 P1井产能曲线

表3 P1井回压试井无阻流量误差数据表

从表3可知，利用经验数0.083计算的无阻流量相对误差小于2.19%，满足工业要求，且由于第三组数据误差最小，所以选第三组数据作为分析数据。用同样方法从9口测试井中选出误差最小的一组数据见表4。

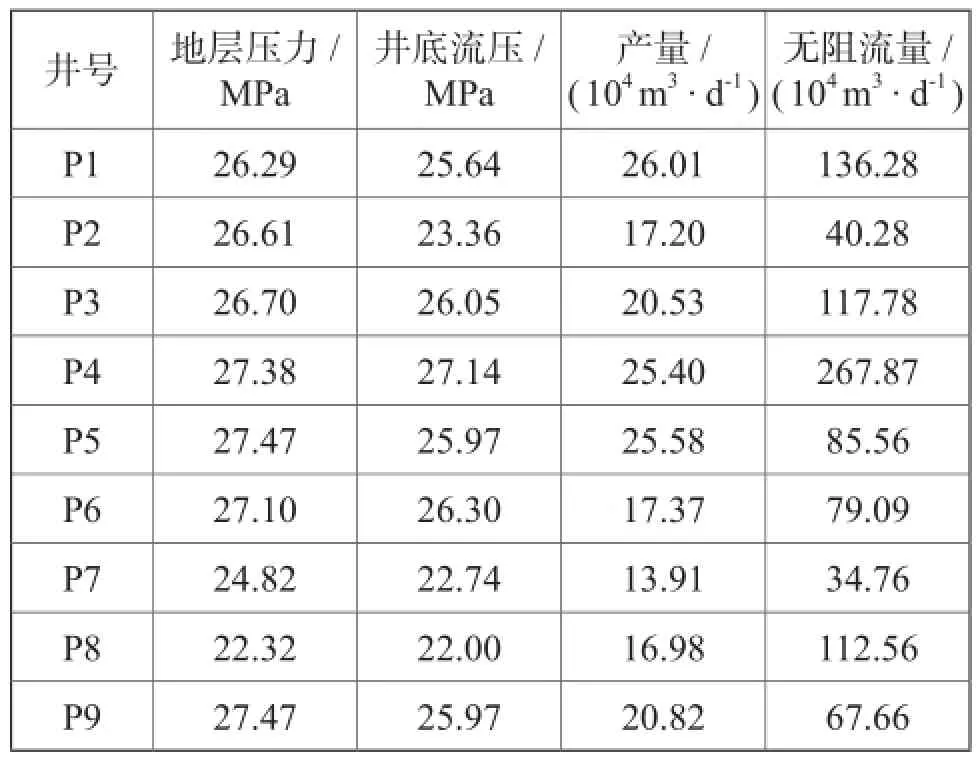
表4 X气田产能试井数据表

利用本文方法，绘制经验数与无阻流量平均误差和均方差的关系曲线，如图3所示，最优经验数为0.083，无阻流量误差为4.3%。图1比较了最优经验数（0.083）、平均经验数（0.2）和陈元千经验数（0.25）时统计井无阻流量的相对误差，最优经验数下预测的无阻流量误差均小于10%，平均误差为4.3%，比经验数为0.2时精度提高了27.7%，比经验数为0.25时精度提高了40.7%。

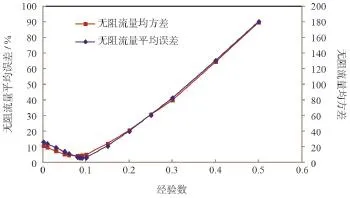
图3 无阻流量平均相对误差和均方差随经验数变化曲线

2.2 Y气田

Y气田在1995 ～ 2015年期间进行了10口井产能测试，其产能方程、无阻流量和经验数如表5。

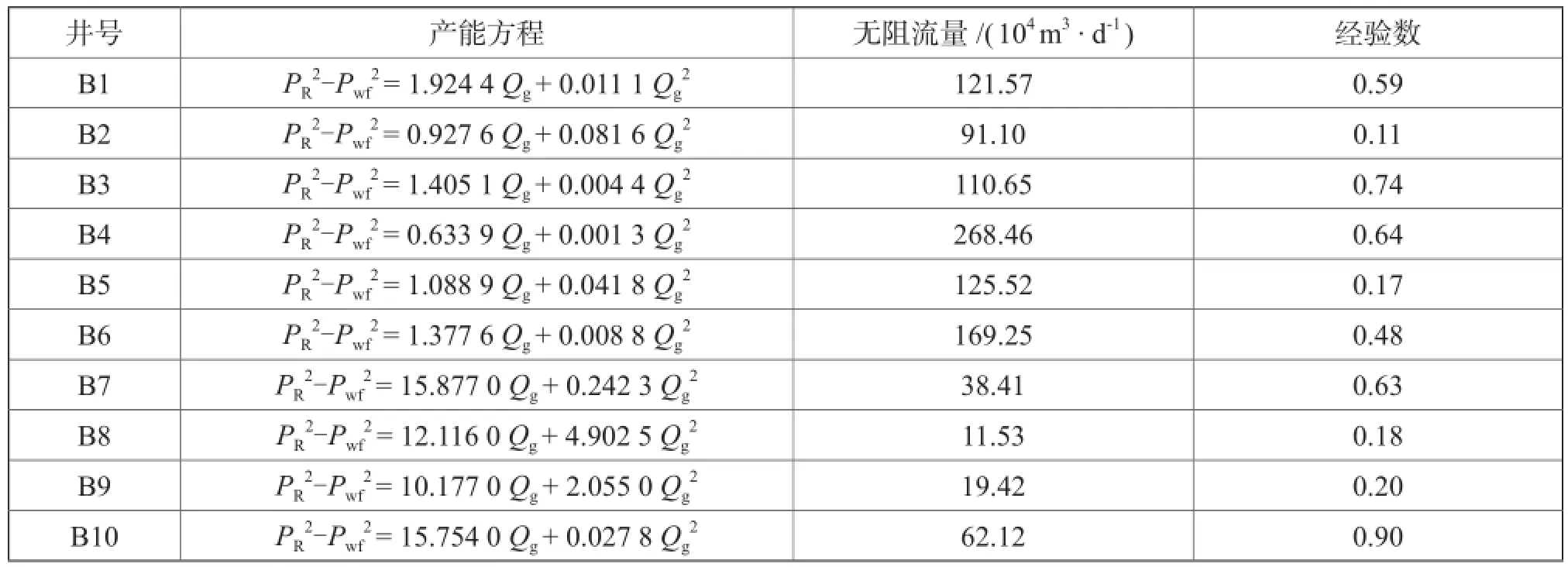
表5 Y气田多点法产能试井数据表

从表5可知，10口井的平均经验数为0.464，该经验数和陈元千经验数下气井无阻流量的相对误差如图4所示。经验数为0.464时无阻流量误差集中在3% ～ 107%，平均误差高达55%；陈元千方法（经验数为0.25时）无阻流量误差3% ～ 37%，平均误差为20%。下面用本文方法进行气井产能评价。

与X气田相似，同样取Y气田10口井中无阻流量误差最小的一组数据统计见表6。

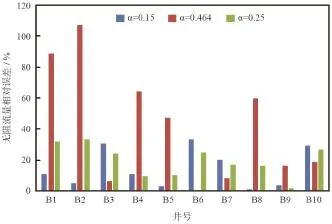
图4 Y气田气井无阻流量相对误差直方图

绘制经验数与无阻流量平均误差和均方差的关系曲线，如图5所示，最优经验数为0.15，无阻流量平均误差为15%。图4比较了最优经验数（0.15）、平均经验数（0.464）和陈元千经验数（0.25）时统计井无阻流量的误差，最优经验数下预测的无阻流量误差均小于30%，平均误差为15%，比经验数为0.464时精度提高了40%。

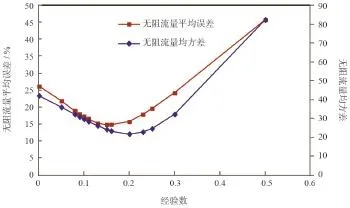
图5 无阻流量平均误差和均方差随经验数变化曲线

图1 和图4曲线可以反映经验数从0到1范围时，已测试井的产能误差和均方差范围，如果产能误差和均方差较小说明气田适合一点法产能评价方法（如X气田），如果产能误差和均方差较大说明气田不适用于一点法产能评价方法（如Y气田）。

3 结论

结合HD海域气田的测试现状，更深入地研究了一点法经验数的优化方法，得到如下成果与结论：

（1）建立了气藏一点法经验数优化方法。结合多点法产能试井资料，利用最小二乘法原理，比较气井实际无阻流量和经验数计算无阻流量，以无阻流量误差及均方差最小为目标，优化经验数。

（2）X气田9口井平均经验数为0.2，计算无阻流量的误差范围为14% ～ 50%，平均误差高达32%；Y气田10口井的经验数为0.464，计算无阻流量误差主要集中在3% ～ 107%，平均误差高达55%。故取统计井经验数平均值预测无阻流量误差较大，不满足工业要求。

（3）X气田最优经验数为0.083，无阻流量平均误差为4.3%，与常规方法相比产能评价精度提高了27.7%。Y气田最优经验数为0.15，无阻流量平均误差为15%，与常规方法相比产能评价精度提高了40%。

[1]李士伦. 天然气工程[M]. 北京： 石油工业出版社， 2008.

[2]方军成， 王念喜， 伊超. 大牛地气田一点法产能结果评价[J].天然气工业， 2007， 27（12）： 121-123.

[3]王富平， 黄全华， 孙雷， 等. 低渗透气藏气井一点法产能预测公式[J]. 新疆石油地质， 2010， 31（6）： 652-653.

[4]王富平， 黄全华. 产水气井一点法产能预测公式[J]. 新疆石油地质， 2009， 30（1）： 86-86.

[5]胡建国， 张宗林， 张振文. 气田一点法产能试井资料处理新方法[J]. 天然气工业， 2008， 28（2）： 111-113.

[6]李进、马旸、杨志华. 一种基于“一点法”的气井产能试井资料处理方法[J]. 新疆石油地质， 2010， 31（3）： 331-331.

[7]许进进， 李志平， 赖枫鹏， 等. 一点法试井资料处理新方法[J].油气井测试， 2006， 15（4）： 20-21.

[8]藤赛男， 梁景伟， 李元生， 等. 气井一点法试井资料处理方法评价[J]. 新疆石油地质， 2012， 33（1）： 92-94.

[9]陈元千. 确定气井绝对无阻流量的简单方法[J]. 天然气工业，1987， 7（1）： 59-63.

[10]王军民， 张公社， 陆小锋， 等.“ 一点法”方程在普光气田中的改进[J]. 内蒙古石油化工， 2010， 36（23）： 126-127.

[11]曹继华， 刘俊丰， 李伟. 一点法试井在台南气田的应用及校正[J]. 岩性油气藏， 2010， 22（S1）： 104-106.

[12]韩会玲， 蒋建方， 杨玉凤， 等.“ 一点法”快速试气在陕北气田的应用研究[J]. 油气井测试， 2008， 17（5）： 17-19， 23.

[13]傅诚德. 鄂尔多斯深盆气研究[M]. 北京： 石油工业出版社，2001.

[14]陆书柱. 一点法试井技术在气藏勘探中的应用[J]. 油气井测试， 1996（4）： 55-62.

Optimization Method of Empirical Coefficient in Single-point Method: A Case Study in the Gas Field of HD Sea Area

TENG Sainan1, LI Yuansheng2
（1. Institute of Explorition and Development, SINOPEC Shanghai Offshore Oil & Gas Company, Shanghai 200120, China；2. Shanghai Branch of CNOOC Ltd., Shanghai 200030, China）

Back-pressure test and single-point test have been extensively implemented the Gas field of HD Sea Area. There is more than 20% of average error occurred when the open-flow capacity of a gas well was predicted by the empirical coefficient of Chen Yuanqian or average empirical coefficient obtained from gas wells that have back-pressure test data. In view of this, the authors tried to look for a method that can optimize the empirical coefficient in the single-point method and minimize the error of open flow capacity calculated. Case study of X gas field and Y gas field show that the optimal empirical coefficient are 0.083 and 0.15 respectively, and the average error of open flow potential are 4.3% and 15% respectively, which are 27.7% and 40% less than that of the conventional method, respectively. The study of this paper not only improves the accuracy of capacity evaluation by single-point method, but also can enhance the adaptability of single-point in the gas field.

Capacity evaluation by single-point method; empirical coefficient; optimized method

TE32

A

10.3969/j.issn.1008-2336.2016.04.056

1008-2336（2016）04-0056-05

2016-06-14；改回日期：2016-09-09

藤赛男，女，1986年生，工程师，从事油藏工程研究工作。

E-mail：tengsn.shhy@sinopec.com。